理数答案_2024年4月_01按日期_16号_2024届四川绵阳南山中学高三4月绵阳三诊热身考试_四川省绵阳南山中学2024届高三下学期4月绵阳三诊热身考试数学（理）

2021级高三下期绵阳三诊热身考试试题
理科数学参考答案
一、单选题
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 A A A B C C C B A D A D
二、填空题
 2  32π
13．30 14.3 15. , 16.
ln2  3
三、解答题
17．（Ⅰ）由题意，得0.020.032a0.018101， 解得a0.03；
又由最高矩形中点的的横坐标为20，可估计盒子中小球重量的众数约为20（克）
而50个样本小球重量的平均值为：X 0.2100.32200.3300.184024.6（克）
故由样本估计总体，可估计盒子中小球重量的平均值约为24.6克；
（Ⅱ）利用样本估计总体，该盒子中小球重量在5,15 内的概率为0.2
1
则X B(3, ).X 的可能取值为0、1、2、3，
5
0 3 2
1 4 64 1 4 48
PX 0C0      ，PX 1C1     ，
3 5 5 125 35 5 125
2 3 0
1 4 12 1 4 1
PX 2C2     ，PX 3C3      .
3 5 5 125 35 5 125
X 的分布列为：
X 0 1 2 3
64 48 12 1
P
125 125 125 125
64 48 12 1 3 1 3
EX 0 1 2 3  .（或者EX 3  ）
125 125 125 125 5 5 5
S  S S
18．（1）设等差数列 n的公差为d，则 4  1 3d，即S 3d 5，①
 n  4 1 1
S S
因为S a a S  4，所以由 2  1 d ，得S 2d 4．②
2 1 2 1 2 1 1
试卷第1页，共6页
{#{QQABCQiAggiAAIIAARgCUQXyCkAQkBACAIoOQAAEoAAByAFABAA=}#}S
由①、②解得S 2,d 1，所以 n n1，即S nn1，
1 n
n
当n2时，a S S nn1n1n2n，
n n n1
当n1时，a S 2，上式也成立，
1 1
所以a 2n  nN* ，所以数列a 是等差数列；
n n
b a 2n n
（2）由（1）可知 n1  n   ，
b a 2n4 n2
n n2
b b b n1 n2 1 12
当n2时，b  n  n1 2b     6 ，
n b b b 1 n 1 n 3 n n 1
n1 n2 1
因为b 6满足上式，所以b 
12
12


1

1 


n
N*
．
1 n nn1 n n1
 1 1 1 1 1   1  12
T 121      121 12 ．
n  2 2 3  n n1  n1 n1
19．（1）证明：因为AC2BC2，所以BC1.
 
因为2ACB ，所以ACB .
3 6
1 2
BC AC 
在ABC中，  ，即  sinB ，所以sinB1，即ABBC.
sinA sinB sin
6
又因为平面ABC平面BCCB，平面ABC平面BCCB BC ，AB平面ABC，
1 1 1 1
所以AB平面BCCB.
1 1
又BC平面BCCB，所以ABBC，
1 1 1 1

在BBC中，BB2，BC1，CBB  ，
1 1 1 3

所以BC2 BB2BC22BBBCcos 3，即BC  3，所以BC BC.
1 1 1 3 1 1
而ABBC，AB平面ABC，BC平面ABC，ABBCB，
1
所以BC平面ABC.
1
又BC平面ACB ，所以平面ABC平面ACB .
1 1 1
试卷第2页，共6页
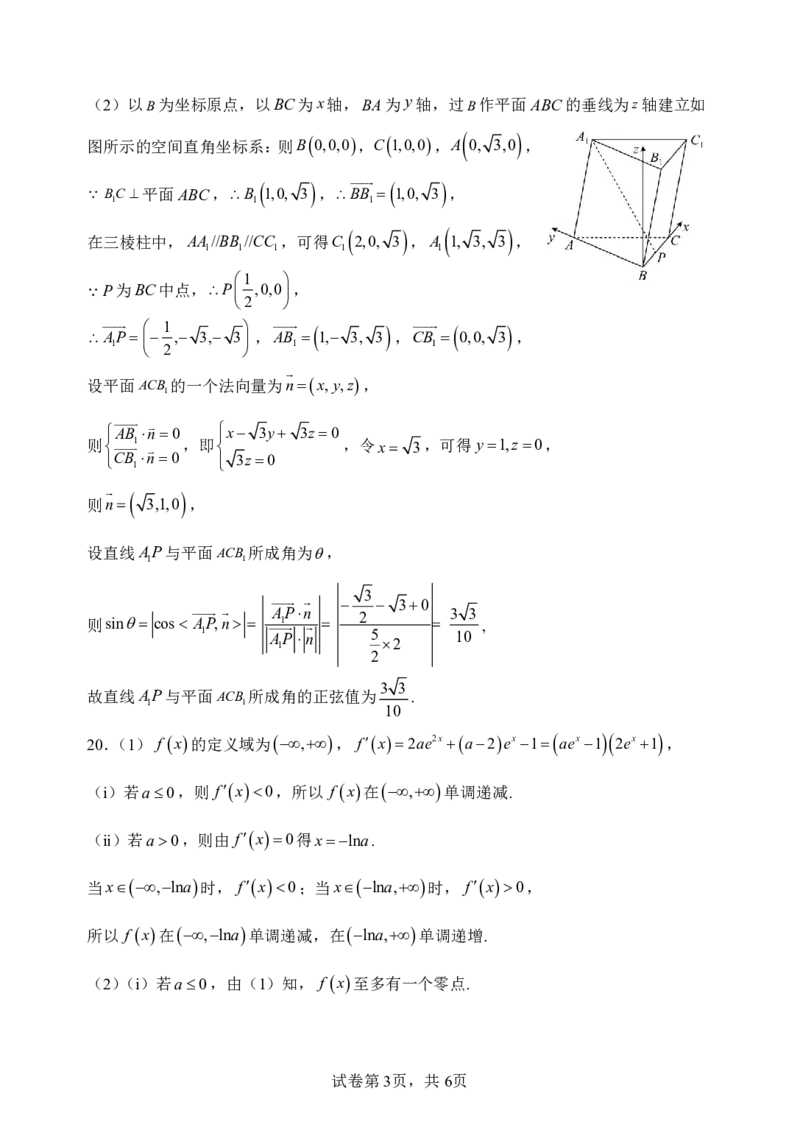
{#{QQABCQiAggiAAIIAARgCUQXyCkAQkBACAIoOQAAEoAAByAFABAA=}#}（2）以B为坐标原点，以BC为x轴，BA为y轴，过B作平面ABC的垂线为z轴建立如
图所示的空间直角坐标系：则B  0,0,0，C  1,0,0，A  0, 3,0  ，

   
 BC平面ABC，B 1,0, 3 ，BB  1,0, 3 ，
1 1 1
   
在三棱柱中，AA//BB //CC ，可得C 2,0, 3 ，A 1, 3, 3 ，
1 1 1 1 1
1 
P为BC中点，P ,0,0，
2 
  1       
AP , 3, 3 ，AB  1, 3, 3 ，CB  0,0, 3 ，
1  2  1 1

设平面ACB 的一个法向量为nx,y,z，
1
  A  B  n  0  x 3y 3z0
则1

，即 ，令x 3，可得y1,z0，
CB
1
n0  3z0

 
则n 3,1,0 ，
设直线AP与平面ACB 所成角为，
1 1
3
    30
  APn 2 3 3
则sin cos AP,n  1    ,
1 A
1
P n 5 2 10
2
3 3
故直线AP与平面ACB 所成角的正弦值为 .
1 1
10
20．（1） f x的定义域为,， fx2ae2x a2ex 1  aex 1  2ex 1  ，
（ⅰ）若a0，则 fx0，所以 f x在,单调递减.
（ⅱ）若a0，则由 fx0得xlna.
当x,lna时， fx0；当xlna,时， fx0，
所以 f x在,lna单调递减，在lna,单调递增.
（2）（ⅰ）若a0，由（1）知， f x至多有一个零点.
试卷第3页，共6页
{#{QQABCQiAggiAAIIAARgCUQXyCkAQkBACAIoOQAAEoAAByAFABAA=}#}1
（ⅱ）若a0，由（1）知，当xlna时，f x取得最小值，最小值为 f lna1 lna.
a
①当a1时，由于 f lna0，故 f x只有一个零点；
1
②当a1,时，由于1 lna0，即 f lna0，故 f x没有零点；
a
1
③当a0,1时，1 lna0，即 f lna0.
a
又 f 2ae4a2e222e220，故 f x在,lna有一个零点.
设正整数n 满足n ln   3 1  ，则 f n en0  aen0 a2  n en0 n 2n0 n 0.
0 0 a  0 0 0 0
3 
由于ln 1lna，因此 f x在lna,有一个零点.
a 
综上，a的取值范围为0,1
.
   2
21．（1）将点E 1,2 2 代入抛物线方程，可得 2 2 2p1，解得p4，
所以抛物线方程为y2 8x，
设直线AB的方程为：ykxmk 0,Ax,y ,Bx ,y ，
1 1 2 2
ykxm
联立方程 ，消去y得k2x22km8xm2 0，k 0，
y2 8x
82km m2
由韦达定理得x x  , xx  ，
1 2 k2 1 2 k2
82km 4
根据抛物线定义： AF  BF  x x 4 48，可得m 2k ，
1 2 k2 k
此时Δ2km824k2m2 322km64  k21  0，解得k 1或k 1，
 x x
x  1 2  2
设AB的中点坐标为x ,y ，则 0 2 ，
0 0
 y kx m 2km
0 0
1
可得AB的垂直平分线方程为：y2km x2，
k
4 1
将m 2k 代入整理得：y x6，故AB的垂直平分线过定点6,0．
k k
试卷第4页，共6页
{#{QQABCQiAggiAAIIAARgCUQXyCkAQkBACAIoOQAAEoAAByAFABAA=}#}82km 2 4m2 8 1k2
（2）由（1）可得 AB  1k2     1k2 ，
 k2  k2 k2
1
4 k
且点M6,0到直线AB的距离 6km k ，
d  
1k2 1k2
1
16 k21k
则ABM 的面积为 1 k ，
S  AB d 
2 k2
256  k21  k2 1 2  
可得  k2   1 1 1 ，
S2  2561    
k4  k2 k4 k6
1
设 t，设 f t1tt2t30t1，则 ft12t3t2
k2
1 1
令 ft0，解得0t  ；令 ft0，解得 t 1；
3 3
 1 1 
则 f t在0, 上单调递增，在 ,1上单调递减．
 3 3 
1  2
所以当t  时，ABM 的面积取最大值，此时k2 3，即k  3．此时AB:y 3x .
3  3
 π 1
22．（1）曲线C 的极坐标方程为ρsinθ  0，即sin 3cos10，
1  3 2
则曲线C 的直角坐标方程为 3xy10，
1
把参数方程平方相加得曲线C 的普通方程为x2 y2 4.
2
π
（2）易知点P在直线 3xy10上，且该直线的斜率为
3
，倾斜角为 ，
3
 1
x t

 2
则曲线C 的参数方程为 （t为参数），
1
 3
y1 t
 2
联立曲线C 的参数方程与曲线C 的普通方程得t2 3t30，
1 2
设点A，B在直线 3xy10上对应的参数分别为t ，t ，
1 2
由韦达定理可得t t  3，tt 3，
1 2 12
试卷第5页，共6页
{#{QQABCQiAggiAAIIAARgCUQXyCkAQkBACAIoOQAAEoAAByAFABAA=}#}1 1 1 1 t t t t 3
    2 1  1 2  .
PA PB t t tt tt 3
1 2 12 12
23．（1）因为4x2y2z2 3，所以(2x)2 y2z2 3，
又x、y、z均为正实数，
由柯西不等式有  1212122x2 y2z2  2x y z2，
 
所以2x yz3，当且仅当2x yz且4x2y2z2 3，
即2x y z1时，等号成立，所以2x yz的最大值为3.
（2）因为y2x，x0，y 0，z  0，
由（1）得2x yz4xz3，
1 1
即04xz3，所以  ，
4xz 3
当且仅当2x z1时，等号成立，
1 1 z 4x  z 4x
因为    4xz 5  52  9，
x z x z  x z
4x z
当且仅当  ，即z 2x1时，等号成立，
z x
1 1 1 1 9 1 1
因为  ，所以    3，即  3．
4xz 3 x z 4xz x z
试卷第6页，共6页
{#{QQABCQiAggiAAIIAARgCUQXyCkAQkBACAIoOQAAEoAAByAFABAA=}#}