文档内容
专题 1 数列中的证明问题
新高考在试题形式、试卷结构、难度调控等方面深化改革,数列解答题的难度增加,作为压轴题出现
的概率变大,证明一个数列是等差数列、等比数列或证明数列满足某些条件是数列中的一种重要题型,对
逻辑推理能力要求较高,对式子变形能力要求较高,常出现在解答题第1小题,本专题总结等差数列与等比
数列及其他数列的证明常用方法及技巧.
(一)利用等差数列定义证明数列是等差数列
利用定义法证明 是等差数列,就是证明对任意n∈N*,a -a 是同一常数.
n+1 n
【例1】(2024届四川省自贡市高三第三次诊断)已知数列 的前项和为 ,且 .
(1)证明:数列 为等差数列;
(2)若 , , 成等比数列,求 的最大值.
【解析】(1)数列 满足 ①,
当 时,有 ②,
① ②可得: ,
即 ,变形可得 ,
故数列 是以 为等差的等差数列;
(2)由(1)可知数列 是以 为等差的等差数列,
学科网(北京)股份有限公司若 , , 成等比数列,则有 ,
即 ,解得 ,所以 ,
所以 单调递减,又当 时, ,当 时, ,当 时, ,
故当 或 时, 取得最大值,
且 .
【例2】(2024届河北省沧州市泊头市第一中学等校高三下学期5月高考模拟)已知数列 满足
.
(1)证明:数列 为等差数列,并求 ;
(2)令 ,求数列 的前 项和 .
【解析】(1)由 ,知 ,
所以 ,
所以数列 是以 为首项,-1为公差的等差数列,
所以 ,
所以 .
(2)因为 ,
学科网(北京)股份有限公司所以 .
(二)利用 证明数列是等差数列
若对任意n∈N*,数列 满足2a =a +a,则 是等差数列.
n+1 n+2 n
【例3】已知数列 有 , (常数 ),对任意的正整数n, ,并有 满足
.
(1)求a的值;
(2)证明数列 是等差数列.
【解析】(1)由已知,得 ,
所以 .
(2)由 得 ,则 ,
所以 ,
即 ,
于是有 ,并且有 ,
所以 ,
即 ,
而 是正整数, ,即 ,
所以数列 是等差数列.
(三)证明数列不是等差数列
证明数列不是等差数列,一般只需要证明该数列的连续3项不成等差数列,通常利用反证法证明.
【例4】给定数列 ,若首项 且 ,对任意的 ,都有 ,则称数列 为“指数型
学科网(北京)股份有限公司数列”.
(1)已知数列 为“指数型数列”,若 ,求 ;
(2)已知数列 满足 ,判断数列 是不是“指数型数列”?若是,请
给出证明;若不是,请说明理由;
(3)若数列 是“指数型数列”,且 ,证明:数列 中任意三项都不能构成等差数列.
【证明】(1)因为数列 是“指数型数列”,所以对于任意的 ,
都有 .因为 ,
所以 , .
(2)数列 是“指数型数列”.
证明:由 ,得 ,即 ,
所以数列 是等比数列,且 ,
则 ,
,
所以数列 是“指数型数列”.
(3)因为数列 是“指数型数列”,故对任意的 ,
学科网(北京)股份有限公司有 ,则 ,所以 ,
适合该式.
假设数列 中存在三项 构成等差数列,不妨设 ,
则由 ,得 ,
所以 ,
当 为偶数且 时, 是偶数,而 是奇数, 是偶数,
故 不能成立;
当 为奇数且 时, 是偶数,而 是偶数, 是奇数,
故 不能成立;
所以,对任意的 , 不能成立,
即数列 中任意三项都不能构成等差数列.
(四)利用等比数列的定义证明数列是等比数列
利用定义法证明 是等比数列,就是证明对任意n∈N*, 是同一常数.
【例5】(2024届浙江省北斗星盟高三下学期适应性联考)在直角坐标平面内有线段 ,已知点 是线段
上靠近 的三等分点,点 是线段 上靠近 的三等分点,……,点 是线段 ( ,
)上靠近 的三等分点,设点 的横坐标为 .
(1)求证:数列 为等比数列;
学科网(北京)股份有限公司(2)若 , ,求 的通项公式.
【解析】(1)解:由题意得 所以 ,可得 ,
又由 ,所以
所以数列 是首项为 ,公比为 的等比数列.
(2)解:因为 , ,所以 ,
因为数列 是公比为 的等比数列,所以 时, .
由累加法可得 时,
,即当 时, ,
经检验, 满足上式,所以数列 的通项公式 .
【例6】(2024届湖南师范大学附属中学高三下学期模拟)记 为数列 的前 项和,已知
.
(1)证明:数列 是等比数列;
(2)求最小的正整数 ,使得 对一切 都成立.
【解析】(1)由题知 ,
学科网(北京)股份有限公司用 替换上式的 ,得 .
两式作差, ,即 .
而由 ,可得 .
从而 是首项为 ,公比为 的等比数列.
(2)由(1)得 ,于是 ,
设 ,则 ,
当 时, ,故 ,
两式作差,得 .
整理可得 .
故 ,又 ,因此满足条件的最小正整数 为 .
(五)利用 证明数列是等比数列
若对任意正整数n,都有 ,且 ,则数列 是等比数列.
【例7】(2024届贵州省毕节市高三第三次诊断性)在无穷数列 中,若对任意的 ,都存在 ,
使得 ,则称 为m阶等差数列.在正项无穷数列 中,若对任意的 ,都存在 ,
使得 ,则称 为m阶等比数列.
(1)若数列 为1阶等比数列, , ,求 的通项公式及前n项的和;
学科网(北京)股份有限公司(2)若数列 为m阶等差数列,求证: 为m阶等比数列;
(3)若数列 既是m阶等差数列,又是 阶等差数列,证明: 是等比数列.
【解析】(1)因为 为1阶等比数列,所以 为正项等比数列,
设公比为 ,则 为正数,
由已知得 ,解得 ,
因为 ,所以 ,所以 ,
所以 的通项公式为 ,
前n项的和为 ;
(2)因为 为m阶等差数列,所以对任意的 ,都存在 ,
使得 成立,
所以 ,
即 ,所以 为m阶等比数列;
(3)因为 既是m阶等差数列,又是 阶等差数列,
所以对 ,有 与 同时成立,
所以 与 同时成立,
所以 , , 成等比, , , 成等比,
学科网(北京)股份有限公司由 , , 成等比,得 , , 也成等比,
设 , ,
所以 ,所以数列 是等比数列.
(六)证明数列不是等比数列
证明数列不是等比数列,一般只需要证明该数列的连续3项不成等比数列,通常利用反证法证明.
【例8】(2024届湖北省武汉市高三下学期5月模拟训练)混沌现象普遍存在于自然界和数学模型中,比如
天气预测、种群数量变化和天体运动等等,其中一维线段上的抛物线映射是混沌动力学中最基础应用最广泛
的模型之一,假设在一个混沌系统中,用 来表示系统在第 个时刻的状态值,且该系统下一时刻的状
态 满足 , ,其中 .
(1)当 时,若满足对 ,有 ,求 的通项公式;
(2)证明:当 时, 中不存在连续的三项构成等比数列;
(3)若 , ,记 ,证明: .
【解析】(1)当 时, ,依题意, ①, ②,
两式作差, ,则 或 ,
若 ,代入①式解得, 或 ,而 ,于是 ;
若 ,将 代入②式解得, .
因此必有 .
注意到 , ,从而由 归纳即知 是常数列 .
学科网(北京)股份有限公司所以 的通项公式为 .
(2)假设 , , 构成等比数列,则 .
那么由 , 可知 .
又 ,则 ,解得 ,与 矛盾.
所以 中不存在连续的三项构成等比数列.
(3)由于当 时,有 , ,即 .
而 , ,故归纳即知对任意正整数 都有 .
又由 及 可知 ,故数列 单调递减.
又由于 ,故
.
(七)证明数列是新定义的数列
此类问题通常把满足某些条件的数列称为一类新数列,求解关键是证明所给数列满足新数列给定条件
【例9】(2024届山东省枣庄市高三三调)若数列 的各项均为正数,对任意 ,有 ,则称
数列 为“对数凹性”数列.
(1)已知数列1,3,2,4和数列1,2,4,3,2,判断它们是否为“对数凹性”数列,并说明理由;
(2)若函数 有三个零点,其中 .
证明:数列 为“对数凹性”数列;
(3)若数列 的各项均为正数, ,记 的前n项和为 , ,对任意三个不相等正整数p,q,r,存在
学科网(北京)股份有限公司常数t,使得 .
证明:数列 为“对数凹性”数列.
【解析】(1)根据“对数凹性”数列的定义可知数列1,3,2,4中 不成立,
所以数列1,3,2,4不是“对数凹性”数列;
而数列1,2,4,3,2中 均成立,所以数列1,2,4,3,2是“对数凹性”数列;
(2)根据题意及三次函数的性质易知 有两个不等实数根,
所以 ,
又 ,所以 ,
显然 ,即 不是 的零点,
又 ,
令 ,则 也有三个零点,
即 有三个零点,
则 有三个零点,
所以 有两个零点,
所以同上有 ,
故数列 为“对数凹性”数列
(3)将 互换得: ,所以 ,
学科网(北京)股份有限公司令 ,得 ,
所以 ,故数列 是等差数列,
记 ,所以 ,
所以 ,
又因为 ,所以 ,
所以 ,所以 为单调递增的等差数列,
所以 .
所以
所以 ,数列 是“对数凹性”数列.
【例10】(2024届江苏省南京市高三二模)已知数列 的前n项和为 .若对每一个 ,有且仅有
一个 ,使得 ,则称 为“X数列”.记 , ,称数列 为 的“余项数
列”.
(1)若 的前四项依次为0,1, ,1,试判断 是否为“X数列”,并说明理由;
学科网(北京)股份有限公司(2)若 ,证明 为“X数列”,并求它的“余项数列”的通项公式;
(3)已知正项数列 为“X数列”,且 的“余项数列”为等差数列,证明: .
【解析】(1)由题 ,
所以有 , ,
故根据“X数列”的定义 不是“X数列”.
(2)因为 ,
所以当 时, ;
当 时, ;
则 不满足 ,所以 ,
令 ,即 ,
则当 时,有 , ;
当 时,有 ;故 即 ,
则对每一个 ,有且仅有一个 且 ,使得 ,
综上,对任意 ,有且仅有一个 ,使得 ,
所以 为“X数列”,
由上 , ,
即 的“余项数列”通项公式为 , .
学科网(北京)股份有限公司(3)因为 是正项数列,所以 单调递增,
所以 ,故 ,
因为 ,且 为“X数列”,
所以 ,故由 得 ,
的“余项数列” 为等差数列,故其公差 ,
因为 ,所以 ,
若 ,则当 时, ,与 矛盾,
故 ,所以 , ,即 ,
对于 ,若 ,则 ,与正项数列 矛盾,
所以 ,故 ,
所以 ,故 ,
所以 ,
又 ,
所以 , .
(八)证明数列的单调性
证明数列 是递增(减)数列,通常是证明( ),若 ,也可根据 ( )
来证明.
【例11】(2024届湖南省长沙市第一中学高三下学期模拟)已知函数 .
学科网(北京)股份有限公司(1)判断并证明 的零点个数
(2)记 在 上的零点为 ,求证;
(i) 是一个递减数列
(ii) .
【解析】(1)当 为奇数时, 有1个零点;当 为偶数时, 有2个零点.
证明如下:
当 时,由 ,得 ,
所以函数 在 上单调递增,又 , ,
所以函数 在 内有唯一零点;
当 时, ,
若 为奇数, ,则 ,此时 在 内无零点;
若 为偶数,设 ,
则 ,方程 有一个解 ,
所以函数 在 上单调递减,在 上单调递增,
且 ,此时 在 内有1个零点.
综上,当 为奇数时, 有1个零点;当 为偶数时, 有2个零点.
(2)(i)由(1)知,当 时, 在在 内的零点 ,
当 时, , ,
则 ,
故 ,所以数列 是一个递减数列;
学科网(北京)股份有限公司(ii)由(i)知,当 时, ,
当 时, ,
有 ,所以 ,求和可得
,当且仅当 时等号成立;
当 时, ,
故 ,则 ,得 ,
即 ,即 ,即 ,
即 ,即 ,
即 ,当 时, ,
所以当 时,均有 成立,求和可得
.
综上, .
(九)数列中的等式与不等式的证明
数列中的等式证明,通常是根据已知条件进行恒等变形,数列中的不等式证明,常见的是与求和有关的证明,证
明时或者先求和,再放缩,或者先放缩成可求和的数列,再求和.
【例12】(2024届重庆市主城区高三下学期学业质量调研抽测)高斯是德国著名的数学家,近代数学的奠
基者之一,享有“数学王子”的称号,用其名字命名的“高斯函数”定义为:对于任意实数x,记 表示不超
过x的最大整数,则 称为“高斯函数”.例如: , .
(1)设 , ,求证: 是 的一个周期,且 恒成立;
学科网(北京)股份有限公司(2)已知数列 的通项公式为 ,设 .
①求证: ;
②求 的值.
【解析】(1) .
故是 的一个周期.
当 时, , ,故 .
由于周期为 ,故对任意 ,都有 .
(2)①记 .
,则 .
∵
,∴ .
而
.∴ .
学科网(北京)股份有限公司∴ ,∴ .
②由①知 ,则 .
由(1)知:对任意 ,都有 ,
∴ .∴ .
∵ ,∴ .
令 ,
∵ ;
.
∵ ,∴ .
【例1】(2024届辽宁省高考扣题卷二)在直角坐标平面内,将函数 及 在第一象限
内的图象分别记作 , ,点 在 上.过 作平行于x轴的直线,与 交于点 ,再过点
作平行于y轴的直线,与 交于点 .
(1)若 ,请直接写出 , 的值;
学科网(北京)股份有限公司(2)若 ,求证: 是等比数列;
(3)若 ,求证: .
【解析】(1)易知当 时,代入函数解析式可知:
,所以 , .
(2)依题意,由 可得
因为 在 上,所以 ,
又 ,所以 ,整理可得 ,
所以 ①,且 ②,
由 得 ,
又由 ,得 ,即 是以 为公比的等比数列;
(3)若 ,由(2)得 ,
因为 ,所以 ,
学科网(北京)股份有限公司因为 ,所以 ,
又因为 ,
所以
所以 ,从而 ,
所以
从而 |
所以
.
【例2】(2024届黑龙江省高三信息押题卷四)若给定数列 ,对于任意的 ,若满足 ,则
称 为“ 型数列”.若数列 满足: , ,当 时, .
(1)判断数列 是否为“ 型数列”,并证明;
(2)求数列 的通项公式;
(3)若 , ,使不等式 成立,求实数 的取值范围.
【解析】(1)数列 是“ 型数列”,理由如下:
学科网(北京)股份有限公司由 ,得 ,
因为 ,则 ,
所以数列 是首项为2,公比为2的等比数列,
则 , , ,
所以数列 满足“ 型数列”的定义,
即数列 是“ 型数列”.
(2)由(1)知 , ,…, ,
累加得 ,
又 ,所以 .
(3)由(2)可知, ,不等式 有解,
整理为 , 有解,即 ,
设 , ,则 ,
设 , , ,
所以 在 上单调递增,
,所以函数 的值域为 ,
则 ,当 时, ,所以 ,
学科网(北京)股份有限公司所以 的取值范围是 .
【例3】(2024届四川省成都市第七中学高三下学期热身考试)记数列 的前n项和为 ,已知
.
(1)若 ,证明: 是等比数列;
(2)若 是 和 的等差中项,设 ,求数列 的前n项和为 .
【解析】(1)对 ①,当 时,有 ②,
: ,即 ,
经整理,可得 ,
,故 是以 为首项、 为公比的等比数列.
(2)由(1)知 ,有 , ,
题设知 ,即 ,则 ,故 .
而 ,
故 .
【例4】(2024届上海交通大学附属中学高三下学期摸底考试)设 和 是两个等差数列,记
学科网(北京)股份有限公司,其中 表示 , , , 这 个数中最大的
数.
(1)若 , ,求 , , 的值;
(2)若 为常数列,证明 是等差数列;
(3)证明:或者对任意正数 ,存在正整数 ,当 时, ;或者存在正整数 ,使得 , , , ,
是等差数列.
【解析】(1)已知 , ,
, , , , , ,
当 时, ,
当 时, , , ,
当 时, , , , ,
(2)设 ( 为常数), 的通项公式为 .
,
先考虑 ,
则 时, ,
所以 .
当 时,则 , ,
此时 为常数,所以 是等差数列;
当 时,则, ,
此时 是常数列,也是等差数列;
学科网(北京)股份有限公司综上所述: 是等差数列;
(3)设数列 和 的公差分别为 ,
则 ,
所以 ,
①当 时,取正整数 ,则当 时, ,因此 ,
此时, 是等差数列;
②当 时,对任意 ,
此时, 是等差数列;
③当 时,当 时,有 ,
所以
,
对任意正数 ,取正整数 ,
故当 时, .
【例5】(2024届重庆市巴蜀中学校高三下学期模拟)(1)证明:当 时, ;
(2)已知正项数列 满足 .
学科网(北京)股份有限公司(i)证明:数列 为递增数列;
(ii)证明:若 ,则对任意正整数 ,都有 .
【解析】(1)令 ,则 ,
所以 在 上单调递增,所以 ,即 ,
再令 ,则 , ,
令 ,则 ,由上面知 ,
即 在 上单调递减,所以 ,
所以 在 上单调递减,所以 ,
即 .
综上,当 时, 成立.
(2)(i)因为 ,所以 ,
所以 ,由(1)知,当 时, ,
所以 ,
所以数列 为递增数列.
(ii)要证 ,即证 ,即 ,
由(1)知:当 时, ,
所以 ,即有 ,
学科网(北京)股份有限公司所以 ,
所以 ,
又因为 ,所以 ,
所以 ,即 ,
所以 ,归纳易得数列 为减函数,
又数列 为递增数列,
所以 ,
所以
,
又因为 ,
所以 ,
所以 ,
即 成立.
学科网(北京)股份有限公司1.(2024届陕西省安康市高新中学高三模拟)已知数列 满足 .
(1)证明:数列 是等差数列;
(2)设 ,求 的前n项和 .
【解析】(1)证明:令 ,又 ,则有
,
又 ,所以
所以数列 是以1为首项,1为公差的等差数列
(2)由(1)知, ,
又 ,所以 ,
所以 ,
所以
学科网(北京)股份有限公司2.(2024届四川省成都外国语学校高三模拟)已知数列 的前 项和为 ,且满足 .
(1)求证:数列 为等比数列;
(2)已知 ,求数列 的前 项和.
【解析】(1)当 时, ,解得 ,
当 时,由 ,可得 ,
两式相减得 ,所以 ,
又因为 ,所以 是首项为 ,公比为 的等比数列.
(2)由(1)知, ,
所以 ,
数列 的前 项和为 ,
可得 ,
两式相减得 ,
所以 .
3.(2024届安徽省太湖中学高三第四次模拟)已知 .
(1)求 ;
(2)证明: 是等差数列,并求出 ;
学科网(北京)股份有限公司(3)设 ,求 的前 项和 .
【解析】(1) .
(2) ,故 是以1为首项1为公差的等差数列.故
.
(3)因为 ,所以
4.(2025届云南省三校高三联考)绿色已成为当今世界主题,绿色动力已成为时代的驱动力,绿色能源是未
来新能源行业的主导.某汽车公司顺应时代潮流,最新研发了一款新能源汽车,并在出厂前对该批次汽车随机
抽取100辆进行了单次最大续航里程(理论上是指新能源汽车所装载的燃料或电池所能够提供给车行驶的
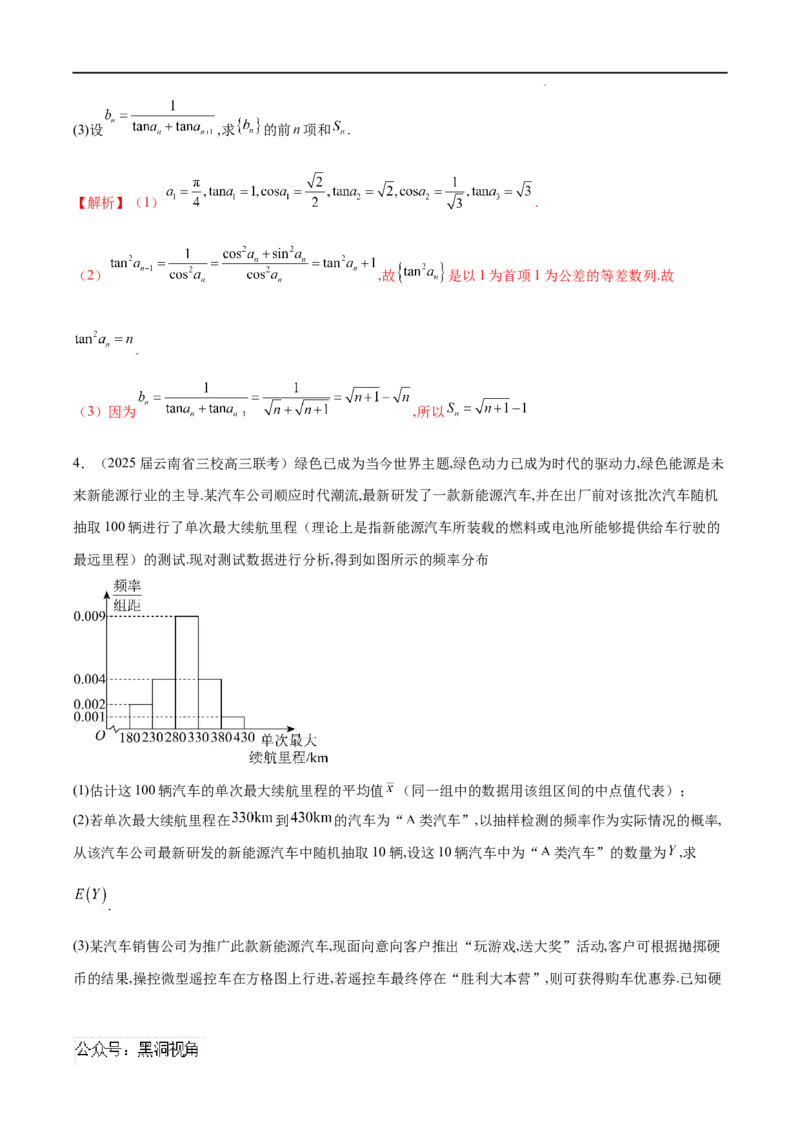
最远里程)的测试.现对测试数据进行分析,得到如图所示的频率分布
(1)估计这100辆汽车的单次最大续航里程的平均值 (同一组中的数据用该组区间的中点值代表);
(2)若单次最大续航里程在 到 的汽车为“ 类汽车”,以抽样检测的频率作为实际情况的概率,
从该汽车公司最新研发的新能源汽车中随机抽取10辆,设这10辆汽车中为“ 类汽车”的数量为 ,求
.
(3)某汽车销售公司为推广此款新能源汽车,现面向意向客户推出“玩游戏,送大奖”活动,客户可根据拋掷硬
币的结果,操控微型遥控车在方格图上行进,若遥控车最终停在“胜利大本营”,则可获得购车优惠券.已知硬
学科网(北京)股份有限公司币出现正、反面的概率都是 ,方格图上标有第0格、第1格、第2格、 、第30格.遥控车开始在第0格,客户每
掷一次硬币,遥控车向前移动一次,若掷出正面,遥控车向前移动一格(从 到 ),若掷出反面,遥控车向前
移动两格(从 到 ),直到遥控车移到第29格(胜利大本营)或第30格(失败大本营)时,游戏结束.
已知遥控车在第0格的概率为 ,设遥控车移到第 格的概率为 ,试证明:数列
是等比数列,并解释此方案能否成功吸引顾客购买该款新能源汽车?
【解析】(1) .
(2)由题意可知任取一辆汽车为“ 类汽车”的概率为 ,
由题设有 ,故 .
(3)第一次掷硬币出现正面,遥控车移到第一格,其概率为 ,即 .
遥控车移到第 格的情况是下面两种,而且只有两种:
①遥控车先到第 格,又掷出反面,其概率为 ;
②遥控车先到第 格,又掷出正面,其概率为 .
所以 ,所以 ,
因为 ,所以 时,数列 是等比数列,
且首项为 ,公比为 ,
所以 .
累加可得:
学科网(北京)股份有限公司,
也满足上式,故 ,
所以获胜的概率 ,
失败的概率 ,
所以 ,
所以获胜的概率大,所以此方案能成功吸引顾客购买该款新能源汽车.
5.(2024届辽宁省实验中学高三下学期考前练)已知数列 满足 , ,令 .
(1)求证:数列 为等差数列;
(2)设 ,数列 的前n项和为 ,定义 为不超过x的最大整数,例如 , ,求数
列 的前n项和 .(参考公式: )
【解析】(1)由题意得 ,代入 得 ,整理得 .
所以 是等差数列;
学科网(北京)股份有限公司(2)由已知 ,又 ,所以 ,
所以 ,
,
所以 , , , ,
时, , ,
所以 , , ,
时, .
6.(2024届上海市七宝中学高三下学期三模)如图,已知正方体 顶点处有一质点 ,点
每次会随机地沿一条棱向相邻的某个顶点移动,且向每个顶点移动的概率相同,从一个顶点沿一条棱移动到
相邻顶点称为移动一次,若质点 的初始位置位于点A处,记点 移动 次后仍在底面 上的概率为 .
(1)求 ;
(2)证明:数列 是等比数列;若 ,求 的最大值.
【解析】(1)依题意,每一个顶点有3个相邻的顶点,其中两个在同一底面,
所以当点 在下底面时,随机移动一次仍在下底面的概率为 ,
学科网(北京)股份有限公司当点 在上底面时,随机移动一次回到下底面的概率为 ,
所以 , .
(2) ,
所以 ,
又因为 ,所以 ,
所以数列 是以 为首项, 为公比的等比数列;
, ,
若 ,则 ,所以 ,
又 , , ,所以 , 的最大值为 .
7.(2024届四川省成都市高三下学期第三次诊断)设 为数列 的前 项和,已知 .
(1)证明: 数列 是等比数列;
(2)设 ,求数列 的前 项和 .
【解析】(1)当 时, ,得 ,
由 ,当 时, ,
两式相减得: ,
整理得: ,
所以 ,且 ,
学科网(北京)股份有限公司是以2为首项,2为公比的等比数列;
(2)由(1)得 ,
,
8.(2024届河南省名校联盟考前模拟大联考三)已知数列 的各项都为正数,且其前 项和
.
(1)证明: 是等差数列,并求 ;
(2)如果 ,求数列 的前 项和 .
【解析】(1)当 时, 或 ,
因为 ,所以 ,
,
两式相减得 ,
因为 ,所以 ,
故 是首项为1,公差为 的等差数列,
;
(2)由(1)知 ,
,
学科网(北京)股份有限公司,
则 ,
,
所以 .
9.(2024届东北三省三校高三第三次联合模拟)已知数列 的前 项和为 ,且 .
(1)求证:数列 是等比数列;
(2)设 ,若 是递增数列,求实数 的范围.
【解析】(1)由 知 ,得 .
由已知有 ,
故 ,得 .
而 ,故数列 是首项为 ,公比为 的等比数列.
(2)根据(1)的结论有 ,即 .
那么就有 .
学科网(北京)股份有限公司命题等价于 恒成立,即 .
此即 ,化简得到 .
从而要求 的取值范围使得 恒成立.
一方面,对该不等式取 可得到 ,即 ;
另一方面,若 ,则 , ,
故我们恒有 ,即 .
所以 的取值范围是 .
10.(2024届河南省九师联盟高三下学期4月质量检测)已知数列 的各项均不为0,其前 项和为 ,
为不等于0的常数,且 .
(1)证明: 是等比数列;
(2)若 成等差数列,则对于任意的正整数 , , , 是否成等差数列?若成等差数列,请予以证明;
若不成等差数列,请说明理由.
【解析】(1)证明:因为 ,①
所以 ,②
② ①,得 ,即 .
当 时, ,即 ,所以 ,
学科网(北京)股份有限公司所以对 , ,即 是公比为 的等比数列.
(2)解:对任意正整数 成等差数列.证明如下:
由 成等差数列,得 ,且 ,
即 ,
化简得 ,即 .
因为 , ,
所以 ,
故对于任意的正整数 成等差数列.
11.(2024届全国统一考试数学押题卷六)已知 为正项数列 的前 项积,且
, .
(1)证明:数列 是等比数列;
(2)若 , 的前 项和为 ,证明: .
【解析】(1)由题意知 ①,
当 时, ,∵ ,∴ .
当 时, ②.
①-②得 , 适合上式,
③,则 ④.
学科网(北京)股份有限公司得 ,∴ ,
两边同时取以 为底的对数,得 ,
则 , ,又 ,
数列 是首项为 ,公比为 的等比数列.
(2)由题意及(1)知 , ,
则 ,
所以 , ,
两式相减得 ,
∴ .
∵ ,
随 的增大而减小,∴ ,又 ,∴ ,
∴ .
12.(2024届辽宁省部分重点中学协作体高三下学期4月三模)若实数列 满足 ,有
,称数列 为“ 数列”.
(1)判断 是否为“ 数列”,并说明理由;
(2)若数列 为“ 数列”,证明:对于任意正整数 ,且 ,都有
学科网(北京)股份有限公司(3)已知数列 为“ 数列”,且 .令 ,其中 表示 中的较大者.证明:
,都有 .
【解析】(1)因为 ,
所以数列 是“ 数列”,
因为 ,
所以数列 不是“ 数列”;
(2)令 ,因为数列 为“ 数列”,所以
从而 ,所以
因为 ,所以
,
因为 ,所以 .
(3)当 或2024时, ,
从而 ,
当 时,因为 ,
由第(2)问的结论得 ,可推得 ,从而
学科网(北京)股份有限公司对于 ,由第(2)问的结论得 ,从而
也成立,从而
对于 ,由第(2)问的结论得 ,从而
也成立,从而
所以
由条件
可得 ,
所以 .
13.(2024届广东省广州市华南师大附中学高三下学期5月月考)对给定的在定义域内连续且存在导函数
的函数 ,若对在 定义域内的给定常数 ,存在数列 满足 在 的定义域内且 ,且对
在区间 的图象上有且仅有在 一个点处的切线平行于 和
学科网(北京)股份有限公司的连线,则称数列 为函数 的“ 关联切线伴随数列”.
(1)若函数 ,证明: 都存在“ 关联切线伴随数列”;
(2)若函数 ,数列 为函数 的“1关联切线伴随数列”,且 ,求 的通项公式;
(3)若函数 ,数列 为函数 的“ 关联切线伴随数列”,记数列 的前 项和为 ,
证明:当 时, .
【解析】(1)因为 ,则 ,
由题意可得: ,
则 ,即 ,且 ,
可知数列 为以 为首项, 为公比的等比数列,
显然这样的数列对于给定的 是存在的,
所以 都存在“ 关联切线伴随数列”.
(2)因为 ,则 ,
设 ,即 ,
由题意可知: ,则 ,
可得 ,且 ,
可知数列 为以 为首项, 为公比的等比数列,
学科网(北京)股份有限公司可得 ,所以数列通项公式为 .
(3)先证明 ,
设函数 ,
则 , ,则 ,
定义 的导函数为 的导函数为 ,
则 ,
且 , ,
令 ,则 ,
,
因为 ,
可知 在 内单调递增,则 ,
同理得 , ,
故 ,
又 在 内单调递增,
在 有 有
因此取 ,有 ,
又 在 单调递减,在 单调递增,
学科网(北京)股份有限公司故 ,
当 时, ,符合题意;
当 时, ,
累加可得 ,
整理得 ,
所以 ;
综上所述: .
14.(2024届山西省部分学校高三年级阶段性测试)对于数列 ,若存在 ,使得对任意 ,总有
,则称 为“有界变差数列”.
(1)若各项均为正数的等比数列 为有界变差数列,求其公比q的取值范围;
(2)若数列 满足 ,且 ,证明: 是有界变差数列;
(3)若 , 均为有界变差数列,且 ,证明: 是有界变差数列.
【解析】(1)因为 的各项均为正数,所以 , ,
,
当 时, , ,任取 即可,所以 为有界变差数列.
学科网(北京)股份有限公司当 时, ,
若 ,则 ,
令 即可,所以 为有界变差数列,
若 ,则 ,当 时, ,
显然不存在符合条件的M,故 不是有界变差数列.
综上,q的取值范围是 .
(2)由 ,可得 ,易知 ,所以 ,
因此 是首项为 ,公差为1的等差数列,
所以 ,即 .
所以 ,
,
所以 是有界变差数列.
(3)由有界变差数列的定义可知,
,
学科网(北京)股份有限公司.
因为
,所以 .
故
,
因此 ,
所以 是有界变差数列.
15.已知数列 的首项 ,且满足 .
(1)证明 是等比数列,并求数列 的通项公式;
(2)是否存在正整数 ,使得对任意的正整数 , 总成立?若存在,求出 的值;若不存在,请说明
理由.
【解析】(1)由 ,得 ,
所以 , 又 ,
故 ,由递推公式可得 ,
学科网(北京)股份有限公司所以 ,
所以 是首项为 、公比为-1的等比数列.
故 ,即 ;
(2)由(1)可得 ,所以
,
假设 成立,
则 ,
化简得 .
可知当 为正偶数,即 时,(*)式对任意的正整数 总成立.
因此,存在正整数 ,当 , 时,对任意的正整数 ,总成立..
16.(2024届山东中学联盟高考考前热身)设 , .如果存在 使得 ,那么就说 可被 整除
(或 整除 ),记做 且称 是 的倍数, 是 的约数(也可称为除数、因数). 不能被 整除就记做
.由整除的定义,不难得出整除的下面几条性质:①若 , ,则 ;② , 互质,若 , ,则
;③若 ,则 ,其中 .
(1)若数列 满足, ,其前 项和为 ,证明: ;
(2)若 为奇数,求证: 能被 整除;
(3)对于整数 与 , ,求证: 可整除 .
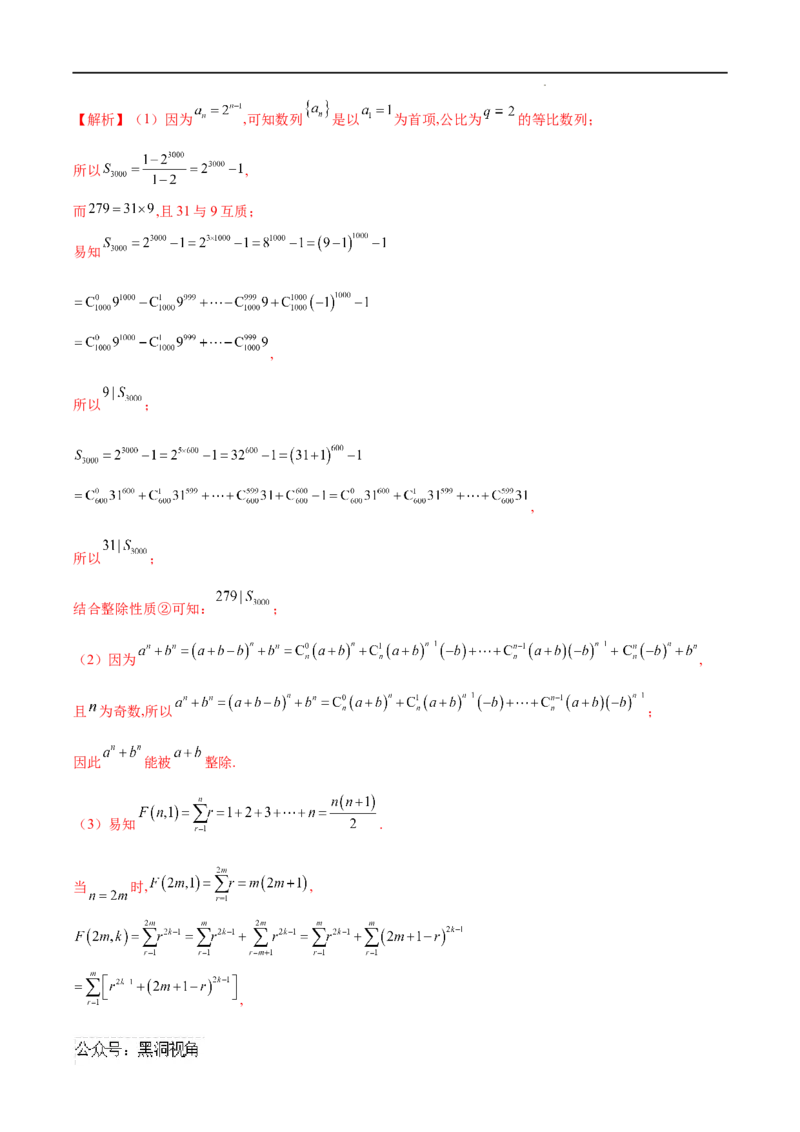
学科网(北京)股份有限公司【解析】(1)因为 ,可知数列 是以 为首项,公比为 的等比数列;
所以 ,
而 ,且31与9互质;
易知
,
所以 ;
,
所以 ;
结合整除性质②可知: ;
(2)因为 ,
且 为奇数,所以 ;
因此 能被 整除.
(3)易知 .
当 时, ,
,
学科网(北京)股份有限公司上式中 ,由(2)知, 能被 整除,
另一方面,
,
上式中 ,所以 也能被 整除,且 与 互质,
所以 能被 整除,即 能被 整除.
类似可证当 时, ,
,
显然 ,由(2)知, 能被 整除;
另一方面,
,
所以 能被 整除;且 与 互质.
能被 整除.
综上可知 能被 整除.
学科网(北京)股份有限公司