文档内容
成都外国语学校 2024—2025 学年度高二上期 10 月月考
数学试卷
注意事项:
1.本试卷分第I卷和第II卷两部分;
2.本堂考试120分钟,满分150分;
3.答题前,考生务必将自己的姓名、学号正确填写在答题卡上,并使用 2B铅
笔填涂;
4.考试结束后,将答题卡交回.
第I卷
一、单选题:本题共8小题,每小题5分,共40分.在每小题给出的选项中,
只有一项符合题目要求.
1.现须完成下列2项抽样调查:①从12瓶饮料中抽取4瓶进行食品卫生检查;②某生活
小区共有540名居民,其中年龄不超过30岁的有180人,年龄在超过30岁不超过60岁的
有270人,60岁以上的有90人,为了解居民对社区环境绿化方面的意见,拟抽取一个容量
为30的样本.较为合理的抽样方法分别为( )
A.①随机数法,②抽签法 B.①随机数法,②分层抽样
C.①抽签法,②分层抽样 D.①抽签法,②随机数法
2.已知向量 , ,且 ,那么实数 等于( )
A.3 B.-3 C.9 D.-9
3.若 是两条不相同的直线, 是两个不同的平面,则下列命题中为真命题的是(
)
A.若 , ,则 B.若 , ,则
C.若 , ,则 D.若 , ,则
4.如图,空间四边形 中, ,点 为 中点,点 在侧棱
上,且 ,则 ( )A. B.
C. D.
5.为了养成良好的运动习惯,某人记录了自己一周内每天的运动时长(单位:分钟),分
别为53,57,45,61,79,49,x,若这组数据的第80百分位数与第60百分位数的差为
3,则 ( )
A.58或64 B.59或64 C.58 D.59
6.已知点 在 确定的平面内, 是平面 外任意一点,正数 满足
,则 的最小值为( )
A. B. C.1 D.2
7.现有一段底面周长为 厘米和高为12厘米的圆柱形水管, 是圆柱的母线,两只蜗
牛分别在水管内壁爬行,一只从 点沿上底部圆弧顺时针方向爬行 厘米后再向下爬行3
厘米到达 点,另一只从 沿下底部圆弧逆时针方向爬行 厘米后再向上爬行3厘米爬行
到达 点,则此时线段 长(单位:厘米)为( )
A. B. C.6 D.12
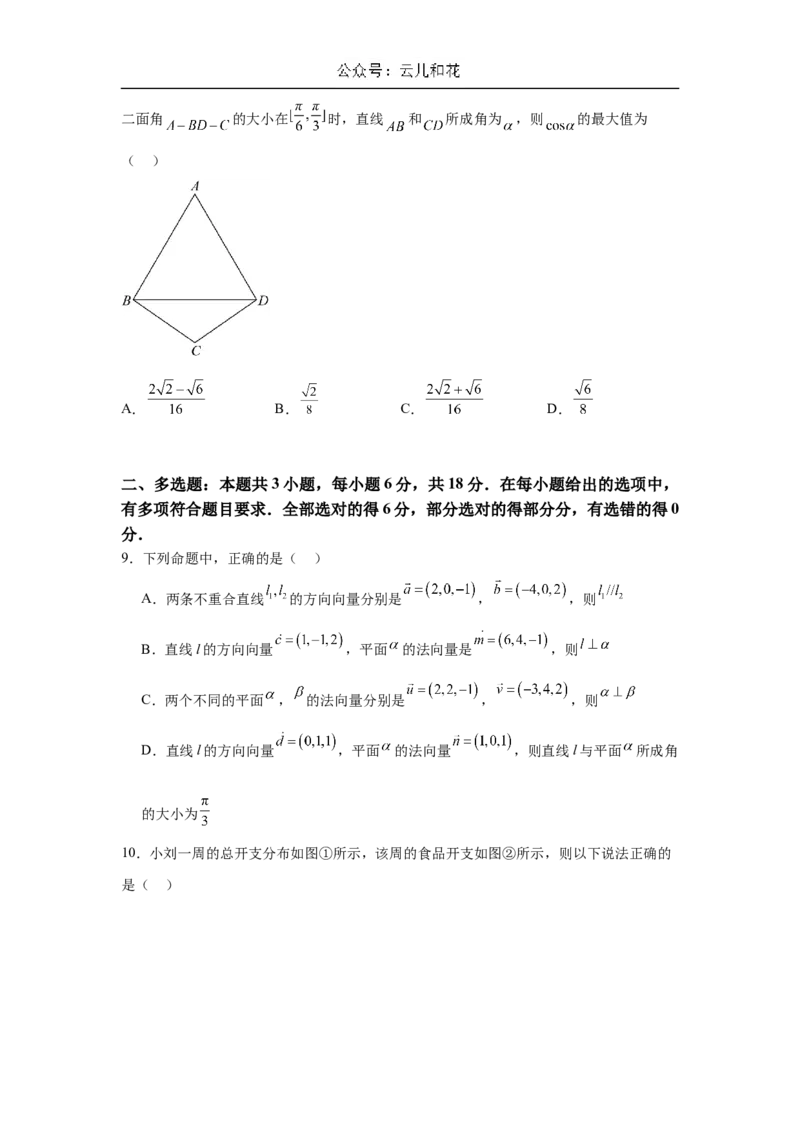
8.如图,四边形 ,现将 沿 折起,当二面角 的大小在 时,直线 和 所成角为 ,则 的最大值为
( )
A. B. C. D.
二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,
有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0
分.
9.下列命题中,正确的是( )
A.两条不重合直线 的方向向量分别是 , ,则
B.直线l的方向向量 ,平面 的法向量是 ,则
C.两个不同的平面 , 的法向量分别是 , ,则
D.直线l的方向向量 ,平面 的法向量 ,则直线l与平面 所成角
的大小为
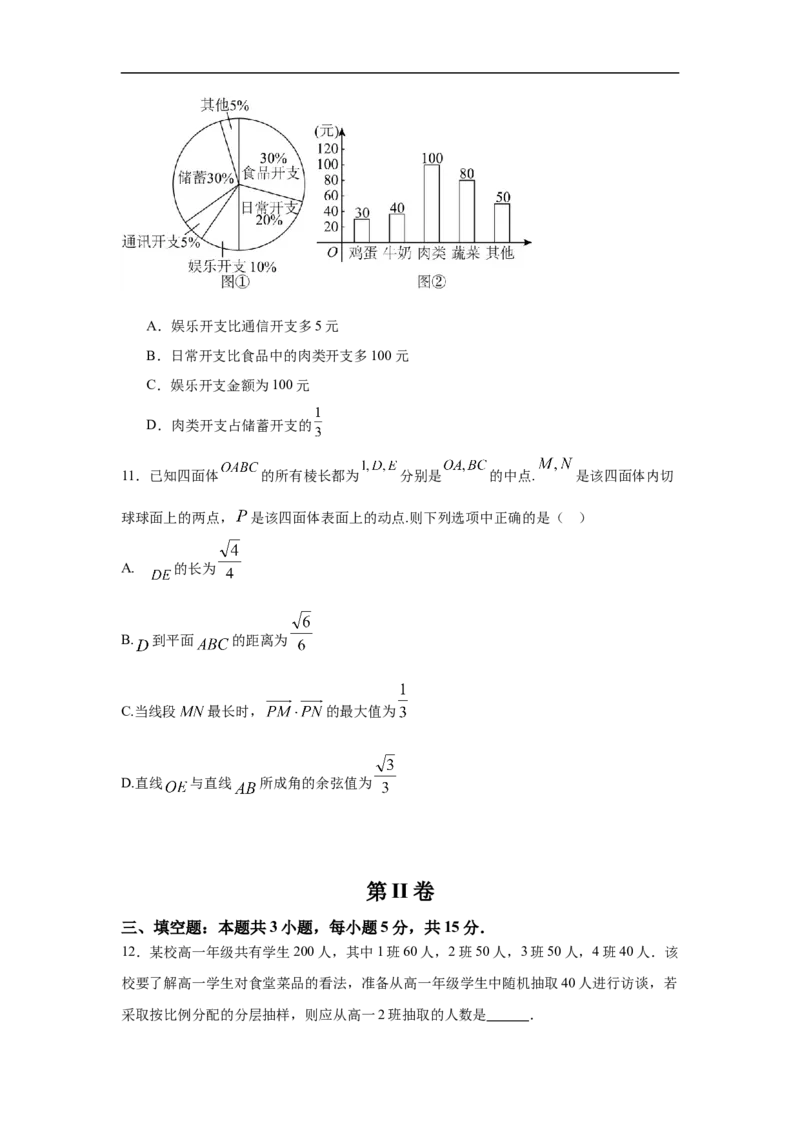
10.小刘一周的总开支分布如图①所示,该周的食品开支如图②所示,则以下说法正确的
是( )A.娱乐开支比通信开支多5元
B.日常开支比食品中的肉类开支多100元
C.娱乐开支金额为100元
D.肉类开支占储蓄开支的
11.已知四面体 的所有棱长都为 分别是 的中点. 是该四面体内切
球球面上的两点, 是该四面体表面上的动点.则下列选项中正确的是( )
A. 的长为
B. 到平面 的距离为
C.当线段 最长时, 的最大值为
D.直线 与直线 所成角的余弦值为
第 II 卷
三、填空题:本题共3小题,每小题5分,共15分.
12.某校高一年级共有学生200人,其中1班60人,2班50人,3班50人,4班40人.该
校要了解高一学生对食堂菜品的看法,准备从高一年级学生中随机抽取40人进行访谈,若
采取按比例分配的分层抽样,则应从高一2班抽取的人数是 .13.已知 , ,若 三向量不能构成空间向量的一组
基底,则实数 的值为 .
14.在正方体 中,点 是 上的动点, 是平面 内的一点,且
满足 ,则平面 与平面 所成角余弦值的最大值为 .
四、解答题:本题共5小题,共77分.解答应写出文字说明,证明过程或演算
步骤.
(满分13分)15.已知向量 , ,
(1)求 的值;
(2)求 ;
(3)求 的最小值.
(满分15分)16.成都市政府委托市电视台进行“创建文明城市”知识问答活动,市电视
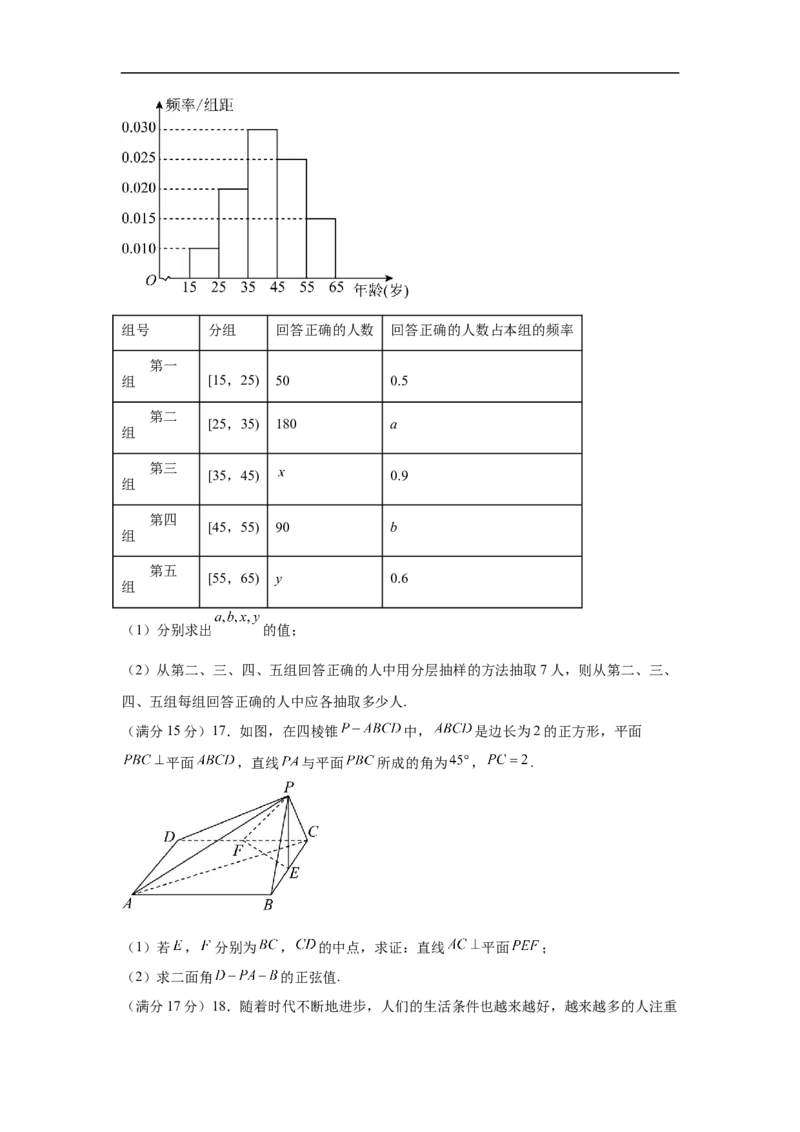
台随机对该市 岁的人群抽取了n人,绘制出如图所示的频率分布直方图,回答问题
的统计结果如表所示.组号 分组 回答正确的人数 回答正确的人数占本组的频率
第一
组 [15,25) 50 0.5
第二
[25,35) 180 a
组
第三
[35,45) 0.9
组
第四
[45,55) 90 b
组
第五
[55,65) y 0.6
组
(1)分别求出 的值;
(2)从第二、三、四、五组回答正确的人中用分层抽样的方法抽取7人,则从第二、三、
四、五组每组回答正确的人中应各抽取多少人.
(满分15分)17.如图,在四棱锥 中, 是边长为2的正方形,平面
平面 ,直线 与平面 所成的角为 , .
(1)若 , 分别为 , 的中点,求证:直线 平面 ;
(2)求二面角 的正弦值.
(满分17分)18.随着时代不断地进步,人们的生活条件也越来越好,越来越多的人注重自己的身材,其中体脂率是一个很重要的衡量标准.根据一般的成人体准,女性体脂率的正
常范围是 至 ,男性的正常范围是 至 .这一范围适用于大多数成年人,可以
帮助判断个体是否存在肥胖的风险.某市有关部门对全市 万名成年女性的体脂率进行一
次抽样调查统计,抽取了 名成年女性的体脂率作为样本绘制频率分布直方图,如图.
(1)求a;
(2)如果女性体脂率为 至 属“偏胖”,体脂率超过 属“过胖”,那么全市女性
“偏胖”,“过胖”各约有多少人?
(3)小王说:“我的体脂率是调查所得数据的中位数.”小张说:“我的体脂率是调查所得数
据的平均数.”那么谁的体脂率更低?(精确到小数点后2位)
(满分17分)19.如图,四面体 中, .
(1)求证:平面 平面 ;
(2)若 ,
①若直线 与平面 所成角为30°,求 的值;
②若 平面 为垂足,直线 与平面 的交点为 .当三棱锥 体
积最大时,求 的值.高二上10月月考数学答案
一、单选题:C D C C A B A B
二、多选题:AC; BCD; BC
√3
3
三、填空题:10; 5;
四、解答题:
15: (1) (2) (3)
16:解:(1)依题和图表:由 得: ,由 得: ,
由 得: ,由 得: ,由 得: ,故
, , , .
(2)由以上知:第二、三、四、五组回答正确的人数分别为:180人,270人,90人,90人用分层抽样抽
取7人,则:从第二组回答正确的人中应该抽取: 人,从第三组回答正确的人中应
该抽取: 人,从第四组回答正确的人中应该抽取: 人,从
第五组回答正确的人中应该抽取: 人,故从第二、三、四、五组每组回答正确的人
中应分别抽取:2人,3人,1人,1人.
17:【详解】(1)证明:∵平面 平面 ,平面 平面 , , 平面
,
∴ 平面 ,则 为直线 与平面 所成的角,为 ,∴ ,而 平面 ,
∴ 又 , 为 的中点,∴ , 平面 ,
则 平面 ,而 平面 ∴ ,又 , 分别为 , 的中点,
则 ,正方形 中, ,∴ ,又 平面 , ,
∴直线 平面 ;
(2)解:以 为坐标原点,分别以 , 所在直线为 , 轴,过 作 的平行线为 轴建立如图所示空间直角坐标系,则 , , , , , ,
,
设平面 的法向量为 ,则 ,即 ,
取 ,得 ;设平面 的法向量为 ,则 ,即
,取 ,得 .
∴ .
∴二面角 的正弦值为 .
18:(1)由频率直方图可得, ,所以 .
(2)由频率分布直方图可得样本中女性“偏胖”的频率为 ,样本中女性“过胖”的频率为
,所以全市女性“偏胖”的人数约为 ,全市女性 “过胖”的人数约为
,
(3)调查所得数据的平均数为 ,设调查所得数
据的中位数为 ,因为 , ,所以 ,所以
,所以 ,所以调查所得数据的中位数约为 ,所以小王的体脂
率约为 ,小张的体脂率为 ,所以小张的体脂率更低.
19:【详解】(1)取 的中点 ,连接 ,因为 ,则 ,所以 ,所以 ,所以 ,又因为 所以 ,
则 ,又因为 ,所以 ,又因为 ,
平面 ,所以 平面 ,又因为 平面 ,所以平面 平面
;
(2)①因为 两两相互垂直,建立如图所示的空间直角坐标系,
所以 ,设 ,因为 ,
所以由 可得: ,所以 ,
,设平面 的法向量为⃗n=(x,y,z),则
,取 ,可得 ,所以 ,
因为直线 与平面 所成角为30°,所以
则 ,化简可得: ,解得: 或 (舍去).
②由(1)知, 平面 ,又 平面
所以 , 在 上,因为 ,所以 ,
,所以 ,即 ,所以 ,
所以 ,三棱锥 体积为:
,
因为 ,当 时,三棱锥 体积最大为 ,此时 分别为 , 的中点,所以, 设 ,设
,
因为 ,所以 ,所以 ,
因为 在平面 上,所以设 ,所以
,所以
,解得: ,所以 ,所以 .