四川省成都市树德中学2024-2025学年高二上学期期中数学试题PDF版含答案_2024-2025高二（7-7月题库）_2024年11月试卷_1108四川省成都市树德中学2024-2025学年高二上学期期中考

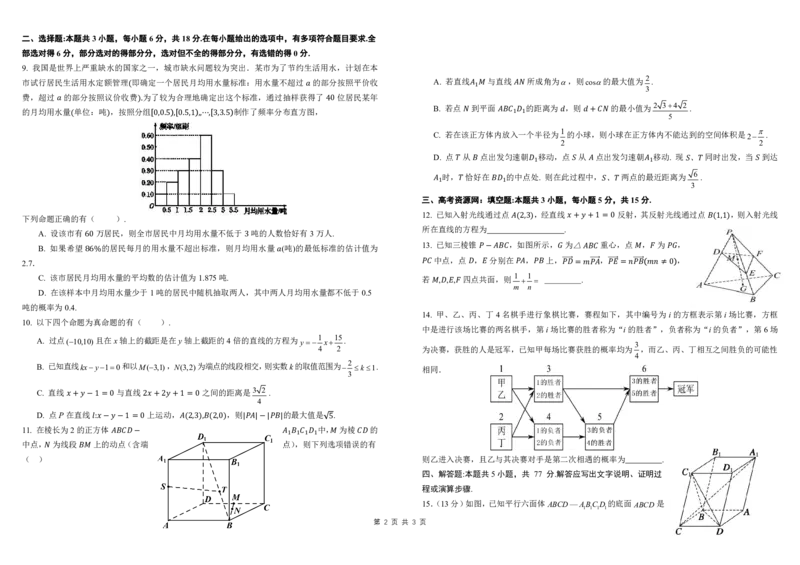
树德中学高 2023 级高二上学期 11 月半期测试数学试题 5. 如图，修水坝时，为了使水坝坚固耐用，必须使水坝面与水平面成适当的角度. 甲站在水库底面上
的点 处，乙站在水坝斜面上的点 处，从 ， 到直线（水库底面与水坝的交线）的距离 和
命题人：朱琨 审题人：邓连康、李小蛟、韦莉
分别为 和 m， 的长为 m，甲乙之间拉紧的绳长为 ，则水库底面与水坝所成二面角的大
考试时间：120分钟 总分：150分  驰  驰 ᜏ 驰ꃰ
小为( )．
一、高考资源网：选择题:本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有个选 t  ᜏꃰ ሺ t
项是正确的，请把正确的选项填涂在答题卡相应的位置上.
11．如图，在平行六面体 中， 为 与 的交点，若 .
则下列向量中与 相等  的 驰ᜏ 向 ꃰ 量  是 (驰ᜏꃰ)  ᜏ 驰ꃰ 驰ꃰ
A.  1 a   1 b  驰   c B. 1 a   1 b  c  A. 30 B. 60 C. 120 D. 150
2 2 2 2
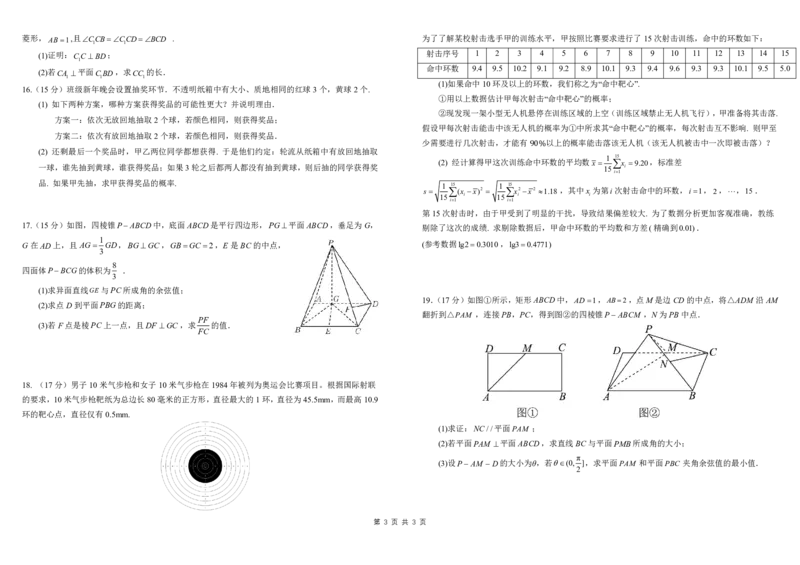
6. 《九章算术》中将底面为直角三角形且侧棱垂直于底面的三棱柱称为“堑堵”；底面为矩形，一条侧
1  1   1  1  
C. a bc D.  a bc 棱垂直于底面的四棱锥称之为“阳马”，四个面均为直角三角形的四面体称为“鳖臑”.如图在堑堵
2 2 2 2
中 .过 点分别作 于点 ， 于点 .下列说法正确的是( )
2. 若直线经过 两点，则直线 的倾斜角是( ) 驰ᜏ
A. 135 B. 120 C. 60 D. 45 驰ᜏ ᜏ 驰ᜏ  驰  tᜏ t
 h 驰ሺ  驰
3. 在长方体ABCDABCD 中，ABBC 1，AA  3，则异面直线AD 与DB 所成角的余弦值为( )
1 1 1 1 1 1 1
2 5 5 5
A. B. C. D. 
2 5 6 5
4. 某年1月25日至2月12日某旅游景区 A 及其里面的特色景点a累计参观人次的折线图如图所示，
则下列判断正确的是( )
A. 四棱锥 为“阳马” B. 四面体 为“鳖臑”
C. ⊥ ᜏ驰驰 D. ᜏᜏ驰
7. 阅读  下 t 面材  料 ᜏ ：在空间直角坐标系Oxyz中，过点Px 0 , t y 0 ,z 0   驰 且一个法向量为m  a,b,c的平面的
方程为axx byy czz 0，过点Px ,y ,z 且方向向量为n  u,v,wuvw0的直线 l
0 0 0 0 0 0
xx yy zz
的方程为 0  0  0 . 根据上述材料，解决下面问题：直线 是两个平面 与
u v w
 ሺꃰڡሺh
的交线，则（ ）是 的一个方向向量.
A. B. C. D.
ሺڡh 
8. 设直  线 ሺ 系  M  :xcosmysinn    1  （ ಀ 其  中,m,n均为参  数  ，  0 ሺ  h   2π,m,n1,  2 ሺ   ） h ，  则  下  列命题中是假 ．
A. 1月29日景区A累计参观人次中特色景点a占比超过了 1 . 命 ． 题 ． 的是（ ）
3
A. 当 mn1 时，存在一个点与直线系M中所有直线的距离都相等.
B. 2月4日至2月10日特色景点a累计参观人次增加了9800人次.
B. 当 mn2 时，直线系M中所有直线恒过定点，且不过第三象限.
C. 2月4日至2月6日特色景点a的累计参观人次的增长率和2月6日至2月8日特色景点a累
2
计参观人次的增长率相等. C. 当mn时，坐标原点到直线系M中所有直线的距离最大值为1，最小值为 .
2
D. 2月8日至2月10日景区A累计参观人次的增长率小于2月6日至2月8日的增长率. D. 当m2,n1时，若 a0 ，则点Aa,0到直线系M中所有直线的距离不小于1.
第 1 页 共 3 页二、选择题:本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求.全
部选对得6分，部分选对的得部分分，选对但不全的得部分分，有选错的得0分.
9. 我国是世界上严重缺水的国家之一，城市缺水问题较为突出．某市为了节约生活用水，计划在本
市试行居民生活用水定额管理 即确定一个居民月均用水量标准：用水量不超过 的部分按照平价收 A. 若直线 与直线 所成角为，则cos的最大值为2 .
3
费，超过 的部分按照议价收  费 为了较为合理地确定出这个标准，通过抽样获  得了 位居民某年  
B. 若点 到平面 的距离为 ，则 的最小值为2 34 2 .
的月均用水量 单位：吨 ，按照分组 制作了频率分布直方图，
 t h 5
 驰ᜏꃰ  ڡᜏ
  hhtಀ  htಀ  tಀ
C.
若在该正方体内放入一个半径为1的小球，则小球在正方体内不能达到的空间体积是
2

.
2 2
D. 点 从 点出发匀速朝 移动，点 从 点出发匀速朝 移动. 现 、 同时出发，当 到达
时， 恰驰好在 的中点ꃰ处  . 则在此过程中， 、 两点的最  近距离为 6. 
3
  驰ꃰ  
三、高考资源网：填空题:本题共3小题，每小题5分，共15分.
12. 已知入射光线通过点 ，经直线 反射，其反射光线通过点 ，则入射光线
下列命题正确的有（ ）.
所在直线的方程为 .
A. 设该市有 万居民，则全市居民中月均用水量不低于 吨的人数恰好有3万人. ሺ ڡꃰڡh 驰
B. 如果希望 的居民每月的用水量不超出标准，则月均用水量 (吨)的最低标准的估计值为 13. 已知三棱锥 ，如图所示， 为△ 重心，点 ， 为 ，
h 
中点，点 ， 分别在 ， 上， ， ，
2.7． ᦙ驰ᜏ  驰ᜏ  t ᦙ
 
C. 该市居民月均用水量的平均数的估计值为1.875吨. ᦙ若ᜏ , , , 四ꃰ点共面，则 1ᦙ 1ᦙ驰 ᦙꃰ.tᦙ ᦙtᦙ驰 tt  h
m n
D. 在该样本中月均用水量少于1吨的居民中随机抽取两人，其中两人月均用水量都不低于0.5
ꃰt
吨的概率为0.4.
14. 甲、乙、丙、丁4名棋手进行象棋比赛，赛程如下，其中编号为i的方框表示第i场比赛，方框
10. 以下四个命题为真命题的有（ ）.
中是进行该场比赛的两名棋手，第i场比赛的胜者称为“i的胜者”，负者称为“i的负者”，第6场
A. 过点(10,10)且在x轴上的截距是在y轴上截距的4倍的直线的方程为 y 1 x 15 .
3
4 2 为决赛，获胜的人是冠军，已知甲每场比赛获胜的概率均为 ，而乙、丙、丁相互之间胜负的可能性
4
B. 已知直线kxy10和以M(3,1)，N(3,2)为端点的线段相交，则实数k的取值范围为 2 k1. 相同．
3
C. 直线 与直线 之间的距离是3 2 .
4
ڡꃰh ሺڡሺꃰڡh
D. 点P在直线 上运动， ，则 的最大值是 .
11. 在棱长为2的正方体 中， 为棱 的
ꃰh ሺ驰ሺh ᦙᦙ驰 ಀ
中点， 为线段 上的动
驰
点
ᜏ
（
ꃰ
含

端

点）
驰
，ᜏ 则ꃰ 下列选

项错误
ᜏ
的
ꃰ
有
（ ） 则乙进入决赛，且乙与其决赛对手是第二次相遇的概率为 .
 驰
四、解答题:本题共5小题，共 77 分.解答应写出文字说明、证明过
程或演算步骤.
15．（13分）如图，已知平行六面体ABCD—ABCD 的底面
ABCD
是
1 1 1 1
第 2 页 共 3 页菱形， AB 1,且CCBCCDBCD . 为了了解某校射击选手甲的训练水平，甲按照比赛要求进行了15次射击训练，命中的环数如下：
1 1
(1)证明：CCBD； 射击序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
1
命中环数 9.4 9.5 10.2 9.1 9.2 8.9 10.1 9.3 9.4 9.6 9.3 9.3 10.1 9.5 5.0
(2)若CA 平面CBD，求CC 的长．
1 1 1
(1)如果命中10环及以上的环数，我们称之为“命中靶心”.
16.（15分）班级新年晚会设置抽奖环节．不透明纸箱中有大小、质地相同的红球3个，黄球2个.
①用以上数据估计甲每次射击“命中靶心”的概率；
(1) 如下两种方案，哪种方案获得奖品的可能性更大？并说明理由．
②现发现一架小型无人机悬停在训练区域的上空（训练区域禁止无人机飞行），甲准备将其击落.
方案一：依次无放回地抽取2个球，若颜色相同，则获得奖品；
假设甲每次射击能击中该无人机的概率为①中所求其“命中靶心”的概率，每次射击互不影响. 则甲至
方案二：依次有放回地抽取2个球，若颜色相同，则获得奖品．
少需要进行几次射击，才能有 以上的概率能击落该无人机（该无人机被击中一次即被击落）？
(2) 还剩最后一个奖品时，甲乙两位同学都想获得. 于是他们约定：轮流从纸箱中有放回地抽取
(2) 经计算得甲这次训练命中h环数的平均数x  1  15 x 9.20，标准差
一球，谁先抽到黄球，谁获得奖品；如果3轮之后都两人都没有抽到黄球，则后抽的同学获得奖 15 i
i1
品. 如果甲先抽，求甲获得奖品的概率.
1 15 1 15
s (x x)2  x2x2 1.18 ，其中x 为第i次射击命中的环数，i1，2，，15．
15 i 15 i i
i1 i1
第15次射击时，由于甲受到了明显的干扰，导致结果偏差较大. 为了数据分析更加客观准确，教练
17.（15分）如图，四棱锥PABCD中，底面ABCD是平行四边形，PG平面ABCD，垂足为G，
剔除了这次的成绩. 求剔除数据后，甲命中环数的平均数和方差(精确到0.01)．
1
G在AD上，且AG GD，BGGC，GBGC2，E是BC的中点， (参考数据lg20.3010，lg30.4771)
3
8
四面体PBCG的体积为 ．
3
(1)求异面直线GE与PC所成角的余弦值；
19．（17分）如图①所示，矩形ABCD中，AD 1，AB2，点M是边CD的中点，将△ADM 沿AM
(2)求点D到平面PBG的距离；
翻折到△PAM ，连接PB，PC，得到图②的四棱锥PABCM ，N为PB中点．
PF
(3)若F点是棱PC上一点，且DF GC，求 的值．
FC
18. （17分）男子10米气步枪和女子10米气步枪在1984年被列为奥运会比赛项目。根据国际射联
的要求，10米气步枪靶纸为总边长80毫米的正方形，直径最大的1环，直径为45.5mm，而最高10.9
环的靶心点，直径仅有0.5mm.
(1)求证：NC//平面PAM ；
(2)若平面PAM 平面ABCD，求直线BC与平面PMB所成角的大小；
π
(3)设P AM D的大小为θ，若(0, ]，求平面PAM 和平面PBC 夹角余弦值的最小值．
2
第 3 页 共 3 页树德中学高 2023 级高二上学期 11 月半期测试数学试题 16. 解： (1)3个红球和2个黄球分别用A,A ,A,B,B 来表示
1 2 3 1 2
参考答案
方案一中，设事件A表示“依次无放回抽取的2个球颜色相同”，
按依次无放回地抽取2个球的所有样本点为A,A ，A,A ，A,B ，A,B ，A ,A，A ,A ，
一、选择题 1 2 1 3 1 1 1 2 2 1 2 3
A ,B ，A ,B ，A,A，A,A ，A,B ，A,B ，B,A，B,A ，B,A ，B,B ，B ,A，
题号 1 2 3 4 5 6 7 8 2 1 2 2 3 1 3 2 3 1 3 2 1 1 1 2 1 3 1 2 2 1
选项 A C B D C D A C B ,A ，B ,A ，B ,B ，共20个；
2 2 2 3 2 1
二、选择题 …………（1分）
题号 9 10 11 事件A包含A,A ，A,A ，A ,A，A ,A ，A,A，A,A ，B,B ，B ,B ，共8个样本
1 2 1 3 2 1 2 3 3 1 3 2 1 2 2 1
选项 BCD CD ACD 点， （2分）
三、填空题
8 2
故PA  ； （3分）
37 20 5
12. 5x4y20 13. 4 14.
128 高考资源网提示：也可按无顺序（即只看抽取结果）的方式计算.
四、解答题
方案二中，设事件B表示“依次有放回地抽取2个球颜色相同”.
15. 苏教版选择性必修二P51,7
3 2

根据题意，每次取到红球的概率为 ，取到黄球的概率为 ，且两次取到球的颜色的情况互不影响，（4分）
解：（1）【法一】设CCB＝CCD＝BCD， |CC |a, 5 5
1 1 1
∴C  C    B  D  C  C    C  D  C  B   C  C  C  D  C  C  C  B  acosacos0 ………（4分） 则PB 3  3  2  2  13 ； ………（6分）
1 1 1 1 5 5 5 5 25
∴C
1
CBD ………（5分） 因为PAPB，所以选择方案二获得奖品的可能性更大． ………（7分）
【法二】连结 AC 和 BD 交于 O ，∵四边形 ABCD 是菱形，∴ AC BD ， BC＝CD ．………（6分） 2
（2）每次抽到黄球的概率为
又∵BCC＝DCC ，CC＝CC，∴ CBC≌CDC， ∴CB＝CD， ………（7分） 5
1 1 1 1 1 1 1 1
∵ DO＝OB ，∴COBD． ………（9分） ①若甲在第一轮就获得奖品，则 p  2 ………（9分）
1 1 5
又COACO，CO、AC平面AACC，∴
BD 
平面AACC， ……（11分）
1 1 1 1 1 1 ②若甲在第二轮获得奖品，则第一轮甲乙均抽到红球，则 p    3  2  2  18 ……（11分）
CC平面AACC，∴CCBD． ……（13分） 2 5 5 125
1 1 1 1
（2）∵四边形 ABCD 是菱形，∴ AC BD,又C 1 CBD ③若甲在第三轮获得奖品，则第一、二轮甲乙均抽到红球，则 p    3  4  2  162 ……（13分）
3 5 5 3125
∴ BD  平面AACC，∴ BD  CA ………（6分）
1 1 1
1862
∴CA 平面CBD的充要条件是CA CB ………（7分） 因此甲获得奖品的概率 p p  p  p  .
1 1 1 1 1 2 3 3125
      
∵
CA CDCBCC
，
CBCBCC
………（8分）
1862
1 1 1 1 所以甲获得奖品的概率为 . ……（15分）
∴ C  A  C  B    C  D  C  B  C  C     C  B  C  C   C  B  2 C  C  2 C  D  C  B  C  D  C  C  3125
1 1 1 1 1 1
1a2cosacos1a1cosa0 ……（11分） 注：也可算乙获得奖品的概率 p
5
3 
5
2   
5
3 

3 
5
2   
5
3 

5  1
3
2
1
6
2
3
5
， p1 p' 1
3
8
1
6
2
2
5
∵ 1cosa0, ∴ a1.
所以CC 的长为1. ……（13分）
1
第 4 页 共 3 页1 1 1 8 1
17. （1）由已知V  S PG   BGGCPG  ,∴PG4 ………（2分） 所以选手每次射击“命中靶心”的概率的估计值 p . （2分）
PBGC 3 BCG 3 2 3 5
如图所示建立空间直角坐标系， ②设该选手至少需要射击n次，才能达到有 以上的概率能击落该无人机，
即他射击n次，至少一次击中无人机的概率在
h90%
以上，
则他这n次射击，没能击中无人机的概率低于 10% ，即   4  n  1 . （4分）
5 10
1 1 1 1
两边取常用对数，得n    10.3， （7分）
lg4lg5 2lg21lg2 13lg2 130.3010
n11.即该选手至少需要射击11次才能达到有 以上的概率能击落该无人机. （8分）
则B(2，0，0),C(0，2，0),P(0，0，4) ,故E（1，1，0）G  E  1,1,0,  P  C  0,2,4 （3分） (2) 剔除数据后，该选手命中环数的平均数x' 1  1 h 5  x  1 159.2059.5 （10分）
14 i 14
  i1
  GEPC 2 10
cos GE,PC      （5分）  15 x2 15  1.182x2 1290.486 （12分）
GE PC 2 20 10 i
i1
14 15
∴异面直线GE与PC所成角的余弦值为
10
（6分）
x
i
2 x
i
252 1265.486 （13分）
10 i1 i1
 14
（2）由题意可知,平面PBG的单位法向量n
0
(0,1,0) （7分） x
i
214x2 1.986 （15分）
i1
 3  3   3 3 
GD  4 BC  2 2,CGD45 ,GD   2 , 2 ,0  （8分） 剔除数据后，该选手命中环数的方差s'2  1    14 x214x2  0.14.
14 i 
i1
  3
∴点D到平面PBG的距离为 GDn
0

2
……（10分）
综上，剔除数据后，该选手命中环数的平均数为9.5，方差约为0.14. ……（17分）
    3 3  3 3  注：方差计算还可以有以下两种方法：
（3）设F（0，y,z）,则DF OFOD0, y, z   , ,0  , y , z, ……（11分）
G  C  0,2,0，  D  F  G  C  ,   D  F  G  C  0  2 2  2 2  ①直接通过原始数据计算 i 1  4 1 x i 9.52 1.94，方差s'2  1 1 4     i 1  4 1 x i 214x2   0.14.
②将前14个数看作一组，剔除的数看作另一组，利用分层抽样总体方差和各层方差的关系：
3 3   3 3
  ,y ,00,2,0 2y 0,解得y ……（13分）
2 2   2 2 s2  14 s'2x'x2 1 05x2
   
15 15
3 1
在平面PGC内过F点作FM GC，M为垂足，则GM  ,MC 
14 1
2 2 1.18 s'29.59.22 059.22
   
15 15
解得 s'2 0.14 .
PF GM
  3. ……（15分）
FC MC
19.解：（1）取 PA 中点Q，连接NQ,MQ，由N为PB中点，得 NQ//AB,NQ 1 AB ，
18. 解：(1)①该选手15次射击中有3次命中10环及以上的环数， 2
第 5 页 共 3 页依题意， MC//AB,MC 1 AB ， 即 x  y  2 (1cos) 2  1 (1cos) ， z  2 sin ，
2 0 0 2 2 2 0 2
则NQ//MC,NQMC， （1分）
所以
P(
1
(1cos),
1
(1cos),
2
sin)
， ……（11分）
于是四边形CMQN 是平行四边形，CN//MQ， （2分） 2 2 2
而MQ平面 PAM ， NC平面 PAM ，所以 NC// 平面 PAM .（3分）
于是 
A

M
 1,1,0， 
P

A

(
1cos
,
cos1
,
2
sin)
，
2 2 2
x y 0
（2）取 AM 中点 G ，连接 PG ，由 PM  PA1 ，得 PG AM ， 设平面PAM的法向量为 ，则  1 1 cos 1 cos1 2sin ，
 x  y  z  0
而平面 PAM  平面 ABCD ，平面 PAM  平面ABCD AM,PG平面 PAM ，则 PG平面 ABCD t ꃰ  2 1 2 1 2 1

过 M 作 Mz//PG ，则 Mz  平面 ABCD ，又MA,MB平面 ABCD ，于是MzMA,MzMB， 令 z 1  2 ，得n 1   tan,tan, 2 ， ……（12分）
在矩形 ABCD 中， MAMB 2 ， MA2MB2 4 AB2 ，则 MAMB ， ………（4分） 设平面 PBC 的法向量为 n  x ,y ,z ，因为 C  B  1,0,0，  P  C  ( cos1 , cos3 , 2 sin) ，
2 2 2 2
以点
M
为原点，直线MA,MB,Mz分别为x,y,z轴建立空间直角坐标系， 2 2 2
x 0
则 M(0,0,0),B(0, 2,0),C( 2 2 , 2 2 ,0),P( 2 2 ,0, 2 2 ) ， 则    c 2 os1 x  cos3 y  2 z sin 0 ，令 y 2  2sin ，得n  2   0, 2sin,3cos ，……（13分）
 2 2 2 2 2 2
M

B

(0, 2,0),M

P

(
2
,0,
2
),

B

C

(
2
,
2
,0)
，………（5分）
设平面 PAM 和平面 PBC 为，
2 2 2 2
m

M

B

 2b0   2
sin2
3 2 2cos
设平面 PMB 的法向量为 m  (a,b,c) ，则     2 2 ， 则 cos  n  1 n  2   cos  3cos1 ……（14分）
mMP a c0 n  n  2tan22  sin26cos10  11cos26cos
 2 2 1 2

令 a1 ，得 m(1,0,1) ， ………（6分） 1
3|cos |
3 3
 
 
2
1 20 1 80 80 20
……（15分）
设直线BC与平面 PMB 所成的角为，则 sin|cosm  ,  B  C  | |  m  B  C  |  2  1，………（7分） (cos 3 )2 3 (cos 3 ) 9 9(cos 1 )2  3(cos 1 ) 1
|m||BC| 21 2
3 3
所以直线BC与平面 PMB 所成角的大小为 π 6 . ………（8分） 令t  1 1 ，(0, π ] ，则 t( 3 ,3] ，即cos 9 ， ……（16分）
cos 2 4 80t260t9
（3）连接 DG ，由 DA DM ，得 DG AM ，而 PG AM ，则PGD 为 3
PAM D 的平面角，即PGD，过点 D 作 Dz  平面 ABCD ，以 D 为坐 则当 t3 时，cos有最小值 11，
11
标原点，直线DA,DC,Dz分别为x,y,z轴建立空间直角坐标系，
所以平面
PAM
和平面
PBC
夹角余弦值的最小值为 11． ……（17分）
则 ， M 0,1,0， C0,2,0 11
显然 AMhh 平面 PGD ， AM  平面 ABCD ，
则平面 PGD平面
ABCD
， ……（9分）
在平面 PGD 内过 P 作 PH DG 于点 H ，则 PH  平面 ABCM ， ……（10分）
设 Px ,y ,z ，而 PG 2 ，则 PH  2 sin ， GH  2 cos ， DH  2 1cos，
0 0 0
2 2 2 2
第 6 页 共 3 页