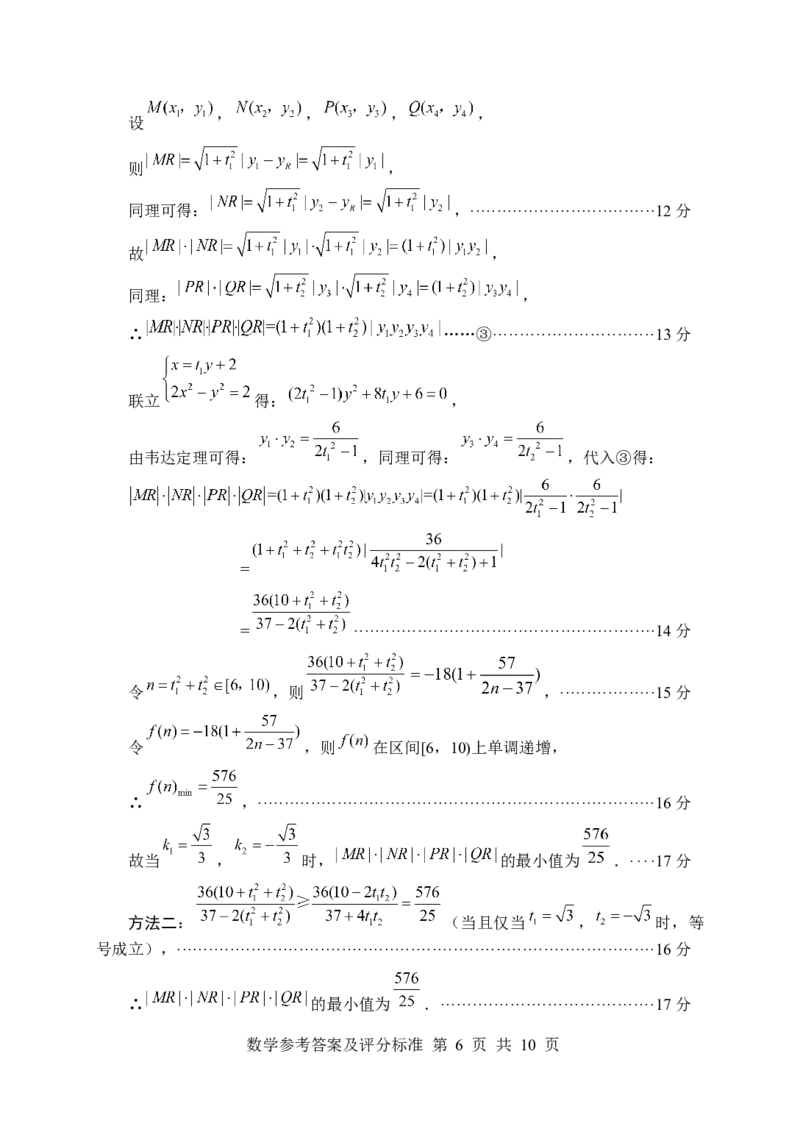文档内容
绵阳市高中 2022 级第三次诊断性考试
数学参考答案及评分标准
一、选择题:本大题共8小题,每小题5分,共40分.
BABC DACC
二、选择题:本题共3小题,每小题6分,共18分.
9.ACD 10.AB 11.AB
三、填空题:本大题共3小题,每小题5分,共15分.
12.−8 13.0.42 14.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.解:(1)设数列公比为 ,
由 , , 成等差数列得: ,····································3分
∴ ,即: ,可得 ,····························5分
数列{a}的通项公式为: ;························································6分
n
(2)
······························································7分
······························································8分
···························································9分
············································································11分
(或 ).··················································13分
数学参考答案及评分标准 第 1 页 共 10 页16.解:(1) ,令 ,···········································1分
∵函数 在 处取得极值.
,则 ,······································································2分
∴
,······················································3分
令 ,可得 ,或 ,·····················································4分
, , 单调递增;
, , 单调递减;················································5分
, , 单调递增,············································6分
∴ 的极小值为 ;···············································7分
(2)由(1)可知 在[1,2]上单调递减,········································8分
∴ , ,················································9分
∴ ,·······················································10分
∴ ···············································13分
∴当 , .············································15分
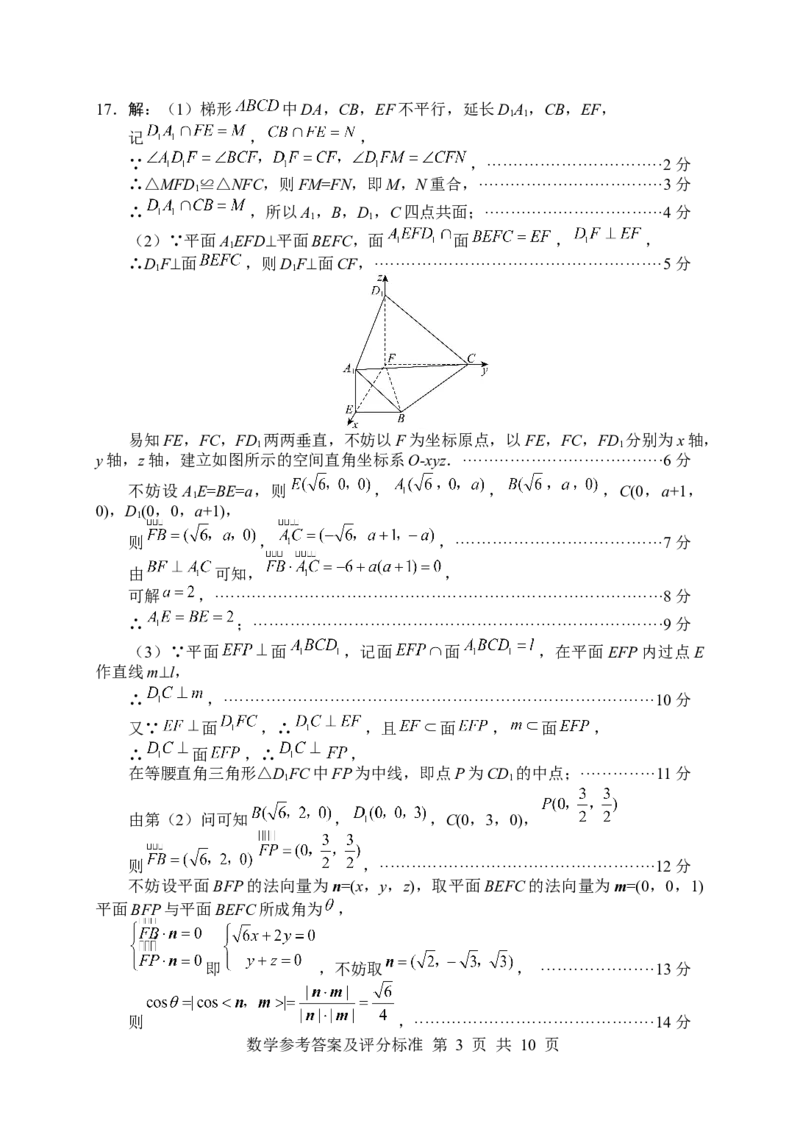
数学参考答案及评分标准 第 2 页 共 10 页17.解:(1)梯形 中DA,CB,EF不平行,延长DA,CB,EF,
1 1
记 , ,
∵ ,·································2分
∴△MFD≌△NFC,则FM=FN,即M,N重合,···································3分
1
∴ ,所以A,B,D,C四点共面;··································4分
1 1
(2)∵平面AEFD⊥平面BEFC,面 面 , ,
1
∴DF⊥面 ,则DF⊥面CF,······················································5分
1 1
易知FE,FC,FD 两两垂直,不妨以F为坐标原点,以FE,FC,FD 分别为x轴,
1 1
y轴,z轴,建立如图所示的空间直角坐标系O-xyz.······································6分
不妨设AE=BE=a,则 , , ,C(0,a+1,
1
0),D(0,0,a+1),
1
则 , ,·······································7分
由 可知, ,
可解 ,·····················································································8分
∴ ;·············································································9分
(3)∵平面 面 ,记面 面 ,在平面EFP内过点E
作直线m⊥l,
∴ ,·················································································10分
又∵ 面 ,∴ ,且 面 , 面 ,
∴ 面 ,∴ ,
在等腰直角三角形△DFC中FP为中线,即点P为CD 的中点;··············11分
1 1
由第(2)问可知 , ,C(0,3,0),
则 ,····················································12分
不妨设平面BFP的法向量为n=(x,y,z),取平面BEFC的法向量为m=(0,0,1)
平面BFP与平面BEFC所成角为 ,
即 ,不妨取 , ·····················13分
则 ,·············································14分
数学参考答案及评分标准 第 3 页 共 10 页∴平面BFP与平面BEFC夹角的余弦值为 .····································15分
18.解:(1) ,则 即a=1,····················································1分
又 ,解得 ,··································································2分
∴双曲线C的方程为 .························································3分
2)方法一:设 ,则由 ,
(
可得: ,····················································4分
又点T在双曲线C上,则 ,
化简整理得: ,······························5分
又 , 均在双曲线C上,则 , ,
代入上式整理得: ……①,···········································6分
易知直线l 的斜率为0时,不符合题意,
1
设直线l 方程为 ,则 ,
1
代入①得: ……②
联立 ,得: ,····································7分
由韦达定理可得: ,·················································8分
代入②式得: ,····································9分
解得: ,即 ,此时 ,则直线l 与双曲线C右支有两个交点,
1
数学参考答案及评分标准 第 4 页 共 10 页即直线l 方程为 ;···························································10分
1
方法二:易知直线l 的斜率为0时,不符合题意,设直线l 方程为 ,
1 1
,MN的中点为P(x,y),
0 0
联立 ,得代入①得: ,··········4分
由韦达定理可得: ,·················································5分
∴ , ,···················6分
由 =
则
∴ ,·································································7分
代入双曲线C的方程可得: ,
∴ ,···········································································8分
∴ ,或 ,········································································9分
当 时,直线l 与双曲线的渐进性平行,不符合题意,
1
∴直线l 方程为 ;···························································10分
1
(3)设直线l 方程为 ,直线l 方程为 ,
1 2
由 ,则 ,即 ,································11分
∴ , ,则 (当且仅当 时
取等号)
数学参考答案及评分标准 第 5 页 共 10 页, , , ,
设
则 ,
同理可得: ,···································12分
故 ,
同理: ,
∴ ……③······························13分
联立 得: ,
由韦达定理可得: ,同理可得: ,代入③得:
=
= ·························································14分
令 ,则 ,··················15分
令 ,则 在区间[6,10)上单调递增,
∴ ,···········································································16分
故当 , 时, 的最小值为 .····17分
方法二: (当且仅当 , 时,等
号成立),··························································································16分
∴ 的最小值为 .········································17分
数学参考答案及评分标准 第 6 页 共 10 页数学参考答案及评分标准 第 7 页 共 10 页19.解:(1)当n = 3时,巴士从(0,0)行驶到(2,1)时,共有 种行驶路线;
从(2,1)行驶到(3,3)时,共有 种行驶路线;·································2分
因此经过(2,1)的行驶路线共有 种;···········································4分
(2)(i)方法一:
除去起点A与终点B外,巴士一定会经过7个格点,若游客恰好游览了7个景点,
说明巴士一定不经过AB对角线上的格点.
∴巴士第一步必然到达(1,0)或(0,1)格点,且必然从(4,3)或(3,4)到达终点.在
这个过程中既不会穿过AB对角线,也不会到达对角线上的格点.····················5分
考虑对称性,不妨先计算从格点(1,0)到达格点(4,3),且不经过(1,0)与(4,3)连
线上方格点的路线总数.·········································································6分
假设向右行驶记为1,向上行驶记为−1,那么每条行驶路线实际唯一对应一个含3
个1与3个−1的序列a ,a ,…,a .行驶路线不经过(1,0)与(4,3)连线上方格点,
1 2 6
等价于对任意前k段,向右行驶的段数都不小于向上行驶的段数,即 .
根据题意,满足条件的路线总数应为 种.·····························8分
从而从格点(0,1)到达格点(3,4),且不经过(0,1)与(3,4)连线上方格点的路线总
数也为5种.
因此游客游览了7个景点的路线总数为10种.·······································9分
方法二:当n = 4时,巴士总共有 种行驶路线,··························5分
除去起点A与终点B外,巴士一定会经过7个格点,若游客恰好游览了7个景点,
说明巴士一定不经过AB对角线上的格点,即(1,1),(2,2),(3,3),
设经过格点C(1,1),D(2,2),E(3,3)分别为事件C,D,
E,
C D
则经过格点C的路线总数为 种,
E
经过格点D的路线总数为 种,
经过格点E的路线总数为 种,
经过格点C与格点D的路线总数为 种,
同理 种, 种,
经过格点C,D,E的路线总数为 种,·········7分
因此经过格点C或格点D或格点E的路线总数为:
,8分
用韦恩图可如上图表示,
故游客恰好游览了7个景点的路线总数为 种;·························9分
(ii)要保证游客能够分别浏览两个景区至少1个景点,即行驶路线必须穿过对角
线AB.不妨先考虑只经过AB及其右下方格点的行驶路线,设总数为R(n),假设向右
行驶记为1,向上行驶记为−1,那么每条行驶路线实际唯一对应一个含 n个1与n个
数学参考答案及评分标准 第 8 页 共 10 页−1的序列a,a,…,a .行驶路线不经过AB左上方的格点,等价于对任意前k段,
1 2 2n
向右行驶的段数都不小于向上行驶的段数,即 ,······························10分
····································································11分
由题意
··················································12分
∴行驶路线不经过AB右下方格点的种数也应为 ,
∴行驶路线穿过对角线AB的种数为 ,
故 .
只需证: ,n≥5.·······························13分
当n = 5时, ,上式显然成立.
当n≥6时,令 ,
显然, .············································································14分
且 ,
∵ ( ),当且仅当 时取等,
不难知 ,故 ,·····················15分
所以 ,········16分
即 ,
综上所述: .··········································17分
(注:也可以假设 ,对整理后的一元二次不等式进
数学参考答案及评分标准 第 9 页 共 10 页行验证)
数学参考答案及评分标准 第 10 页 共 10 页