文档内容
数学试卷
注意事项:
1.答题前,考生务必用黑色碳素笔将自己的姓名、准考证号、考场号、座位号在答题卡上填写清
楚.
2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦
干净后,再选涂其他答案标号.在试题卷上作答无效.
3.考试结束后,请将本试卷和答题卡一并交回.满分150分,考试用时120分钟.
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有
一项符合题目要求)
1. 命题“ ”的否定是( )
A. B.
C. D.
【答案】B
【解析】
【分析】利用特称命题的否定规则即可得解.
【详解】命题“ ”的否定是“ ”,
故选:B.
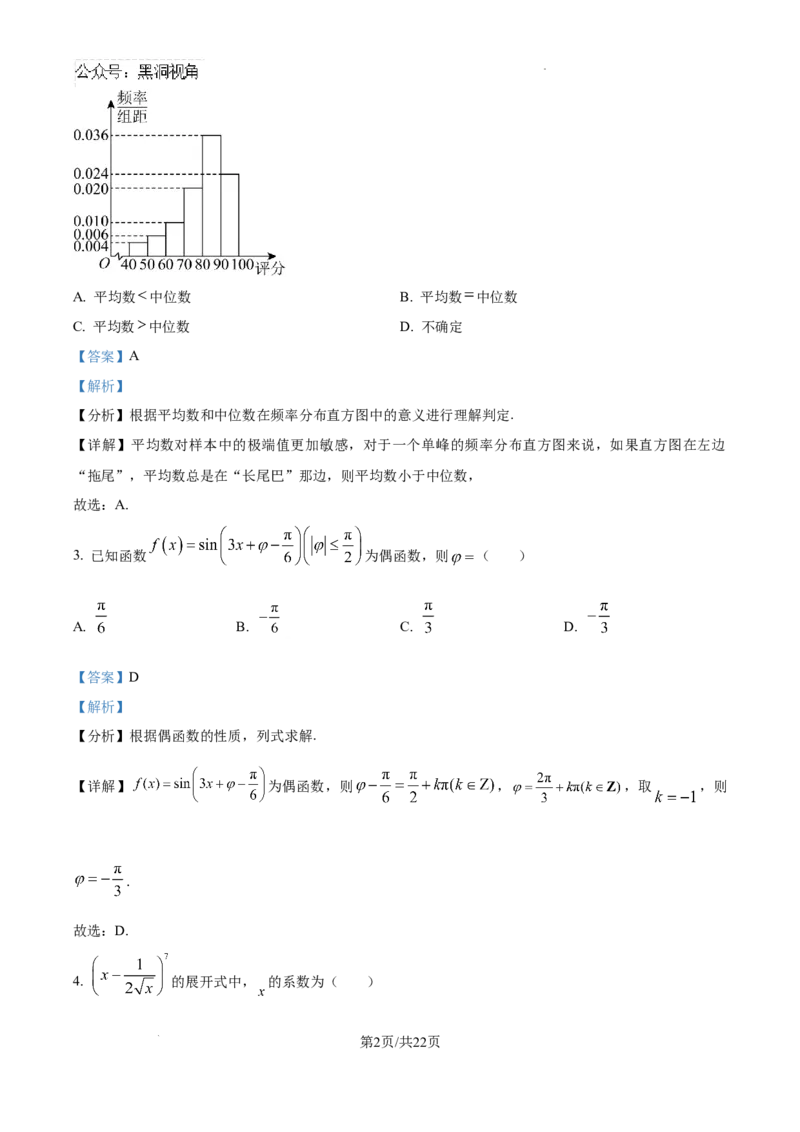
2. 某公司对其新推出的服务系统进行用户满意测评,收集了100位用户的评分数据,整理得如图所示的频
率分布直方图.这组数据的平均数和中位数的大小关系为( )
第1页/共22页
学科网(北京)股份有限公司A. 平均数 中位数 B. 平均数 中位数
C. 平均数 中位数 D. 不确定
【答案】A
【解析】
【分析】根据平均数和中位数在频率分布直方图中的意义进行理解判定.
【详解】平均数对样本中的极端值更加敏感,对于一个单峰的频率分布直方图来说,如果直方图在左边
“拖尾”,平均数总是在“长尾巴”那边,则平均数小于中位数,
故选:A.
3. 已知函数 为偶函数,则 ( )
A. B. C. D.
【答案】D
【解析】
【分析】根据偶函数的性质,列式求解.
【详解】 为偶函数,则 , ,取 ,则
.
故选:D.
4. 的展开式中, 的系数为( )
第2页/共22页
学科网(北京)股份有限公司A. B. C. D.
【答案】C
【解析】
【分析】求出 展开式的通项,再通过令通项中 的次数等于 ,求出对应的 值,最后将 值
代入通项求出 系数.
【详解】 的展开式的通项为 ,令
,解得 ,所以 的系数为 ,
故选:C.
5. 已知 为平面上的点,平面上三点 ,若集合
( 为 所在直线的斜率),则 ( )
.
A B. C. D.
【答案】A
【解析】
【分析】分别求点 , 的轨迹方程,再联立方程求交集.
【详解】由题意可得,点P的轨迹是以 , 为焦点的双曲线的右支,方程为 ,
点Q的轨迹是过点 且斜率为1的直线(不含点 ),方程为 ,
联立方程组 解得 (舍),故 .
故选:A
第3页/共22页
学科网(北京)股份有限公司6. 已知数列 的通项公式为 ,则使 的前 项和 成立的 的( )
(参考数据: )
A. 最小值为7 B. 最大值为7
C. 最小值为8 D. 最大值为8
【答案】C
【解析】
【分析】根据数列 的通项公式求出其前 项和 的表达式,再根据 这个条件解不等式,从
而确定 的取值范围,进而得出 的最小值.
【详解】 ,
故
,
令 ,解得 , ,
解得 , 的最小值为8.
故选:C
7. 口袋中装有大小质地相同的3个白球、5个黑球,逐个取出,直到剩下的球为同一颜色时停止.已知第一
次取出的是白球,则剩下的球是黑球的概率为( )
A. B. C. D.
【答案】C
【解析】
【分析】先确定 和 的值,再代入公式计算 .
第4页/共22页
学科网(北京)股份有限公司【详解】设事件A=“第一次取出的是白球”,B=“剩下的球是黑球”, , ,
所以 , ,
故选:C.
8. 若函数 在 上单调, 为实数,则( )
A. B.
C. D.
【答案】D
【解析】
【分析】对函数 求导,根据函数单调的性质得出 的特点,进而得到 与 的关系,再通过构造
函数,利用导数研究函数单调性来比较 与 、 与 的大小关系.
【详解】 ,
因为 在 上单调,所以 无变号零点,则 是方程 的解,
故 ,即 , ,
令 ,则 ,令 ,解得 ,
时, , 时, ,
所以 在 上单调递增,在 上单调递减, ,
所以 ,即 ; ,
令 , 在 上单调递增,无最值,则 大小不确定,
第5页/共22页
学科网(北京)股份有限公司故选:D.
二、多项选择题(本大题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多
项符合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分)
9. 已知集合 , ,下列对应关系能构成函数的是( )
A. , B. ,
C. , D. ,
【答案】AD
【解析】
【分析】根据函数的定义逐一判断即可.
【详解】对于 , ,则 ,集合 中每个元素,在集合 中都有唯一元素与之对应,
故 正确;
对于 ,取 ,则 ,故 错误;
对于C,取 ,则 ,故C错误;
对于D, , ,集合 中每个元素,在集合 中都有唯一元素与之对应,故D正
确.
故选:AD.
10. 在平面直角坐标系中, 为坐标原点,角 的始边与 轴的非负半轴重合,终边分别与单位圆交于
两点,则下列说法中,正确的是( )
A. 在 上的投影向量为
B.
第6页/共22页
学科网(北京)股份有限公司C. 若 的长度为 ,则 点的轨迹长度为
D. 设 ,则 的最大值为
【答案】ABD
【解析】
【分析】根据向量投影的概念判断A;利用两点间距离结合倍角公式判断B;结合向量的运算,确定P点
轨迹,可判断C;利用三角恒等变换结合三角函数性质可判断D.
【详解】由题意知 ,
则 在 上的投影向量为 ,故A正确;
因为 , ,所以
,故B正确;
当 的长度为 时, ,所以 ,
点轨迹是以 为圆心, 为半径的圆,长度为 ,故C错误;
由于 ,则 ,
则
,
其最大值为 ,当 时取等号,故D正确,
故选:ABD.
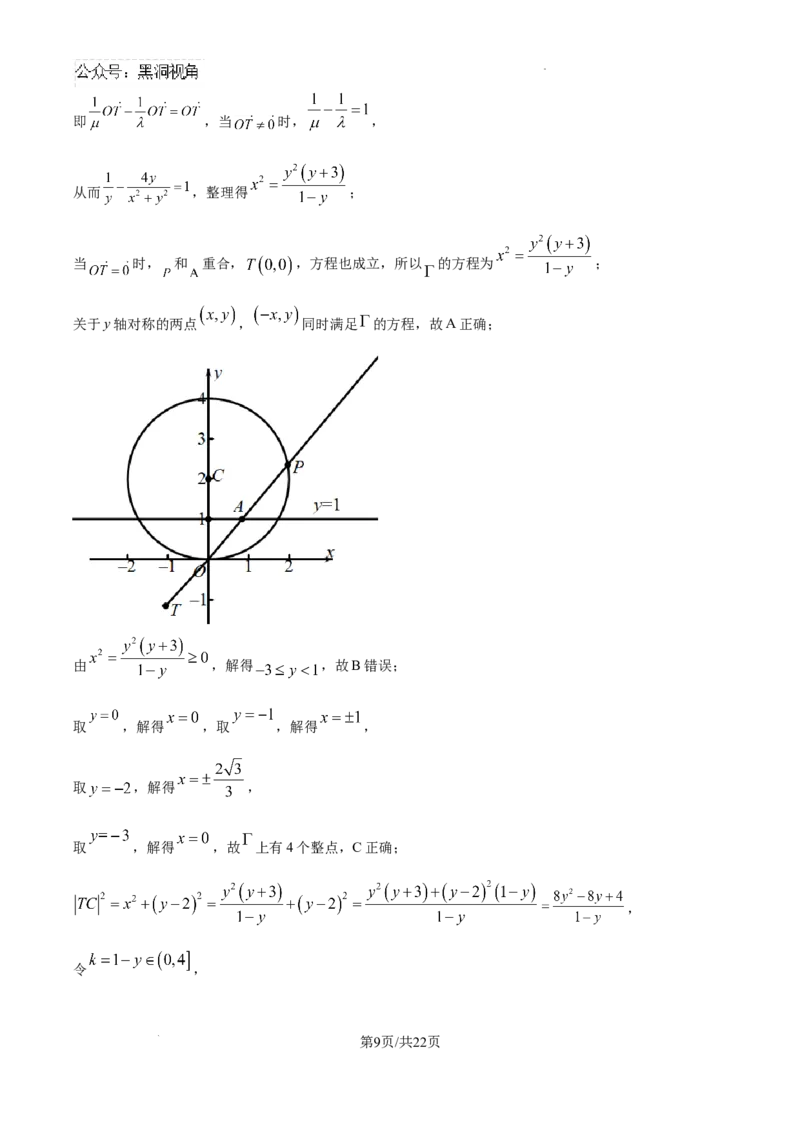
11. 已知 ,直线 , 为原点, 是 上的一个动点,直线 与 交于点
第7页/共22页
学科网(北京)股份有限公司,平面上另一动点 满足 ,点 的轨迹记为曲线 ,则下列说法正确的是( )
A. 曲线 关于 轴对称
B.
C. 上有4个整点(横,纵坐标均为整数的点)
D. 的最小值为
【答案】AC
【解析】
【分析】设 , ,令 ,可得 ,令 可得
,根据 可得 的方程,将两点 , 代入方程即可判断A;由
可得 的范围,即可判断 ;令 , , 即可判断 ;表示 ,利用基本
不等式即可判断 .
【详解】设 , ,令 ,
则 ,即 , ,
因为点 在 上,所以 ,即 ,
解得 (舍)或 ,
令 ,则 ,即 , ,可得 ,
因为 ,所以 ,
第8页/共22页
学科网(北京)股份有限公司即 ,当 时, ,
从而 ,整理得 ;
当 时, 和 重合, ,方程也成立,所以 的方程为 ;
关于y轴对称的两点 , 同时满足 的方程,故A正确;
由 ,解得 ,故B错误;
取 ,解得 ,取 ,解得 ,
取 ,解得 ,
取 ,解得 ,故 上有4个整点,C正确;
,
令 ,
第9页/共22页
学科网(北京)股份有限公司,
当且仅当 时取等号,故 的最小值为 ,D错误.
故选:AC.
【点睛】关键点点睛:解决本题的关键是根据已知向量的关系,得到 的方程,结合方程的解析式和变量
的范围求解.
三、填空题(本大题共3小题,每小题5分,共15分)
12. 若复数 为纯虚数,其中 为虚数单位,则 __________.
【答案】
【解析】
【分析】先通过复数的运算法则将给定的复数化简,再根据纯虚数的定义来确定参数的值.
【详解】因为 为纯虚数,
所以 且 ,解得 .
故答案为:
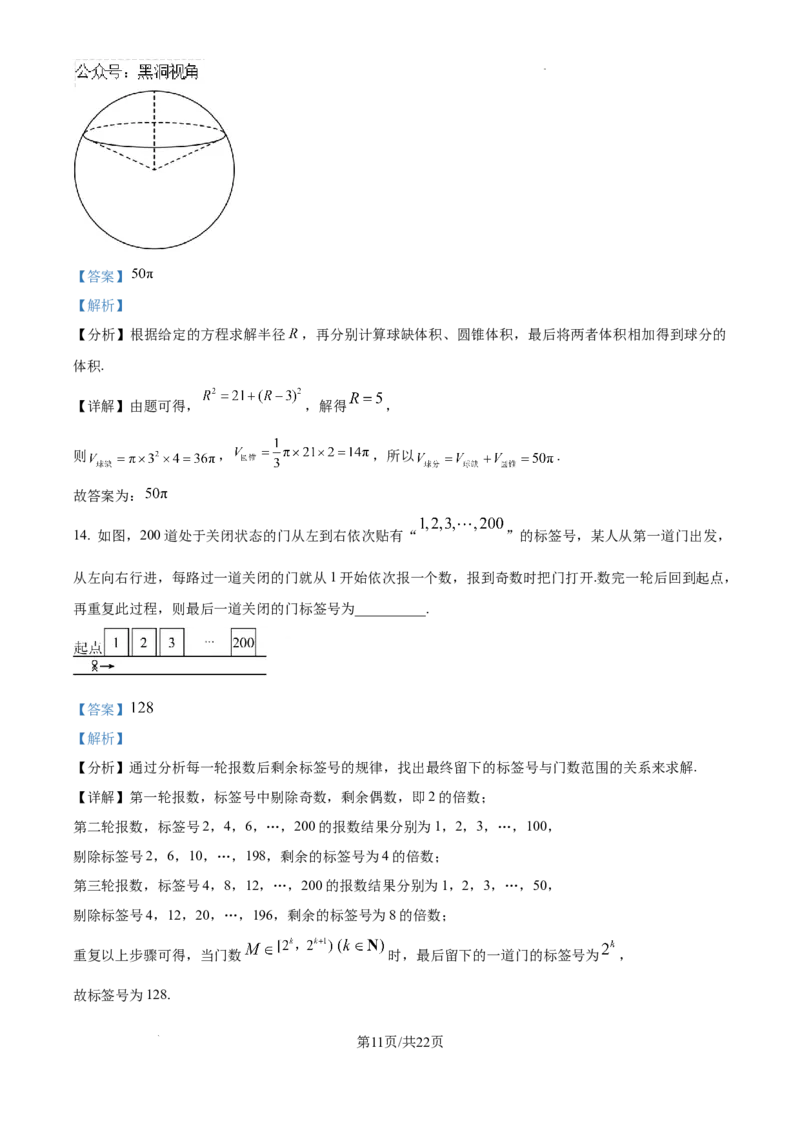
13. 刘徽在《九章算术注》中首次明确提出了球缺和球分的概念,如图,球被平面截取,曲面部分为球冠,
球冠与截面围成的部分为球缺,祖暅精确推导了球缺的体积计算公式为 ,其中 是球的
半径, 是球缺的高(即球冠顶点到截面的距离).连接球心与截面,与球冠围成的部分为球分.若一球缺的
高为3,截面半径为 ,则它对应的球分的体积为__________.
第10页/共22页
学科网(北京)股份有限公司【答案】
【解析】
【分析】根据给定的方程求解半径 ,再分别计算球缺体积、圆锥体积,最后将两者体积相加得到球分的
体积.
【详解】由题可得, ,解得 ,
则 , ,所以 .
故答案为:
14. 如图,200道处于关闭状态的门从左到右依次贴有“ ”的标签号,某人从第一道门出发,
从左向右行进,每路过一道关闭的门就从1开始依次报一个数,报到奇数时把门打开.数完一轮后回到起点,
再重复此过程,则最后一道关闭的门标签号为__________.
【答案】
【解析】
【分析】通过分析每一轮报数后剩余标签号的规律,找出最终留下的标签号与门数范围的关系来求解.
【详解】第一轮报数,标签号中剔除奇数,剩余偶数,即2的倍数;
第二轮报数,标签号2,4,6,…,200的报数结果分别为1,2,3,…,100,
剔除标签号2,6,10,…,198,剩余的标签号为4的倍数;
第三轮报数,标签号4,8,12,…,200的报数结果分别为1,2,3,…,50,
剔除标签号4,12,20,…,196,剩余的标签号为8的倍数;
重复以上步骤可得,当门数 时,最后留下的一道门的标签号为 ,
故标签号为128.
第11页/共22页
学科网(北京)股份有限公司故答案为:128
四、解答题(本大题共5小题,共77分.解答应写出文字说明,证明过程或演算步骤)
15. 在 中,角 所对的边分别为 为边 的中点, ,且
.
(1)求 ;
(2)若 ,求 的面积.
【答案】(1)
(2)
【解析】
【分析】(1)通过正弦定理和余弦定理建立等式,求解出边 的值;
的
(2)利用角 关系和余弦定理建立方程,联立求解出线段长度,进而求出 的三角函数值,最后根
据三角形面积公式求出三角形面积。
【小问1详解】
由正弦定理, ,
由余弦定理, ,
.
所以 ,即 ,解得
【小问2详解】
设 ,
因为 ,所以 ,
解得 ,
第12页/共22页
学科网(北京)股份有限公司在 中, ,
联立方程得 ,解得 , ,
所以 , ,
.
16. 已知 .
(1)当 存在极小值时,求极小值的最值;
(2)若 在 处的切线与 的图象有且仅有一个公共点,求 的
值.
【答案】(1)极小值的最大值为0,无最小值.
(2) .
【解析】
【分析】(1)求出函数的导数,判断函数单调性,可求出函数极值,继而构造函数,求得极值的最值;
(2)根据导数的几何意义求得 在 处的切线,与 联立,讨论
a,结合判别式即可求得答案.
【小问1详解】
, ,
①当 时, 恒成立, 在 上单调递增,无极值;
②当 时,令 ,得 ,
在 上单调递减,在 上单调递增,无极大值,
第13页/共22页
学科网(北京)股份有限公司极小值为 ,
令 ,则 ,
因为 ,所以 在 上单调递增,在 上单调递减,
,
综上所述,极小值的最大值为0,无最小值.
【小问2详解】
由题意知 , ,
所以 在 处的切线方程为 ,
联立方程 ,得 ,
当 时,方程仅有一解,符合题意;
当 时,令 ,解得 ,
故 .
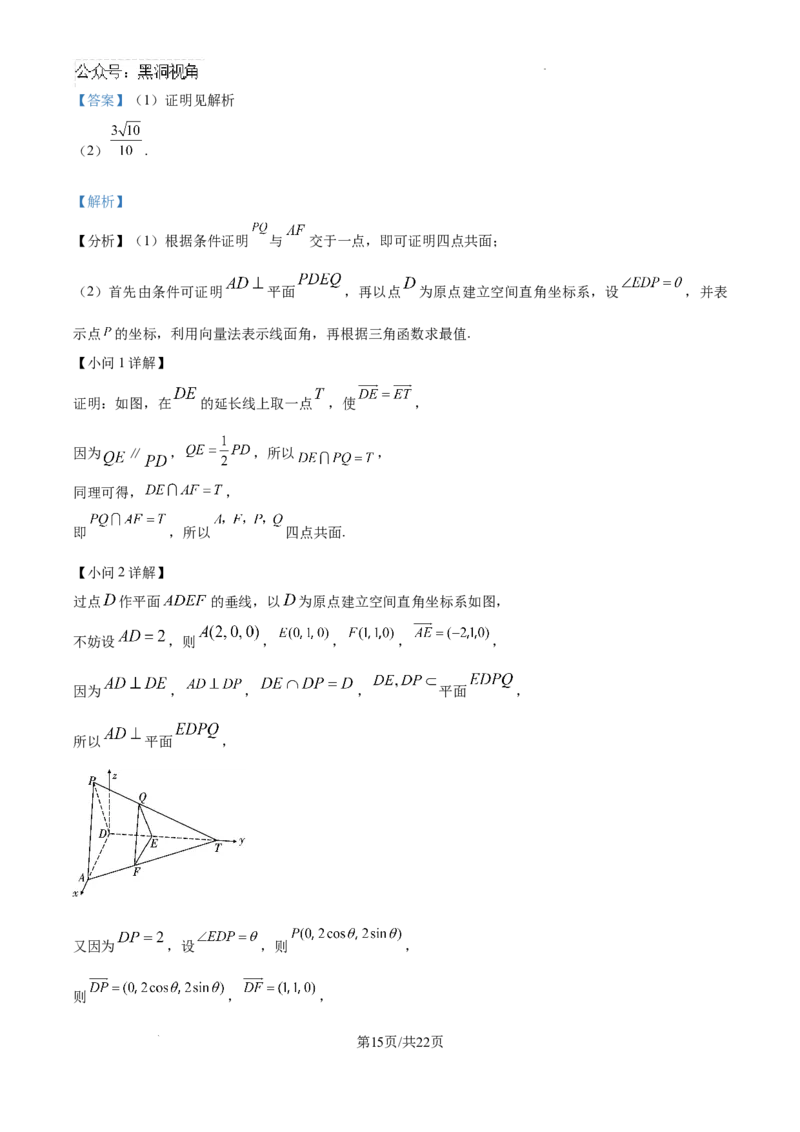
17. 如图甲,在等腰直角 中, ,沿底边的高 与 的中位线 ,分别将 和
折起到 和 的位置,如图乙,折叠过程保持 .
(1)证明: 四点共面;
(2)求直线 与平面 所成角的正弦的最大值.
第14页/共22页
学科网(北京)股份有限公司【答案】(1)证明见解析
(2) .
【解析】
【分析】(1)根据条件证明 与 交于一点,即可证明四点共面;
(2)首先由条件可证明 平面 ,再以点 为原点建立空间直角坐标系,设 ,并表
示点 的坐标,利用向量法表示线面角,再根据三角函数求最值.
【小问1详解】
证明:如图,在 的延长线上取一点 ,使 ,
因为 ∥ , ,所以 ,
同理可得, ,
即 ,所以 四点共面.
【小问2详解】
过点 作平面 的垂线,以 为原点建立空间直角坐标系如图,
不妨设 ,则 , , , ,
因为 , , , 平面 ,
所以 平面 ,
又因为 ,设 ,则 ,
则 , ,
第15页/共22页
学科网(北京)股份有限公司设平面 的法向量为 ,则
令 ,得 ,
设 与平面 所成的角为 ,
则 ,
因为 ,所以 ,当且仅当 时取等,
所以直线 与平面 所成角正弦的最大值为 .
18. 椭圆 的长轴在 轴上,长轴长为4,离心率为 .
(1)求椭圆 的方程;
(2)若直线 与 交于 ,直线 与 交于
.
①证明: ;
②设直线 与直线 轴分别交于点 ,求 的值.
【答案】(1)
(2)①证明见解析;② .
第16页/共22页
学科网(北京)股份有限公司【解析】
【分析】(1)根据离心率公式和长轴长计算即可;
(2)①直曲联立,结合韦达定理计算即可;
②设 , ,由 三点共线,构造方程,
解得 ,同理可得, ,结合①结论,得到 ,化简即可.
【小问1详解】
解:设 的方程为 ,
则 解得 ,
所以 的方程为 .
【小问2详解】
①证明:联立方程 可得 ,
恒成立, , ,
则 ,
同理可得, , , ,
第17页/共22页
学科网(北京)股份有限公司所以 .
②解:由题 ,设 , ,
因为 三点共线,所以 ,解得 ,
同理可得, ,
由①得, ,即 ,
,即 ,
所以 ,即 .
【点睛】方法点睛:解决直线与椭圆的综合问题时,要注意:
(1)注意观察应用题设中的每一个条件,明确确定直线、椭圆的条件;
(2)强化有关直线与椭圆联立得出一元二次方程后的运算能力,重视根与系数之间的关系、弦长、斜率、三
角形的面积等问题.
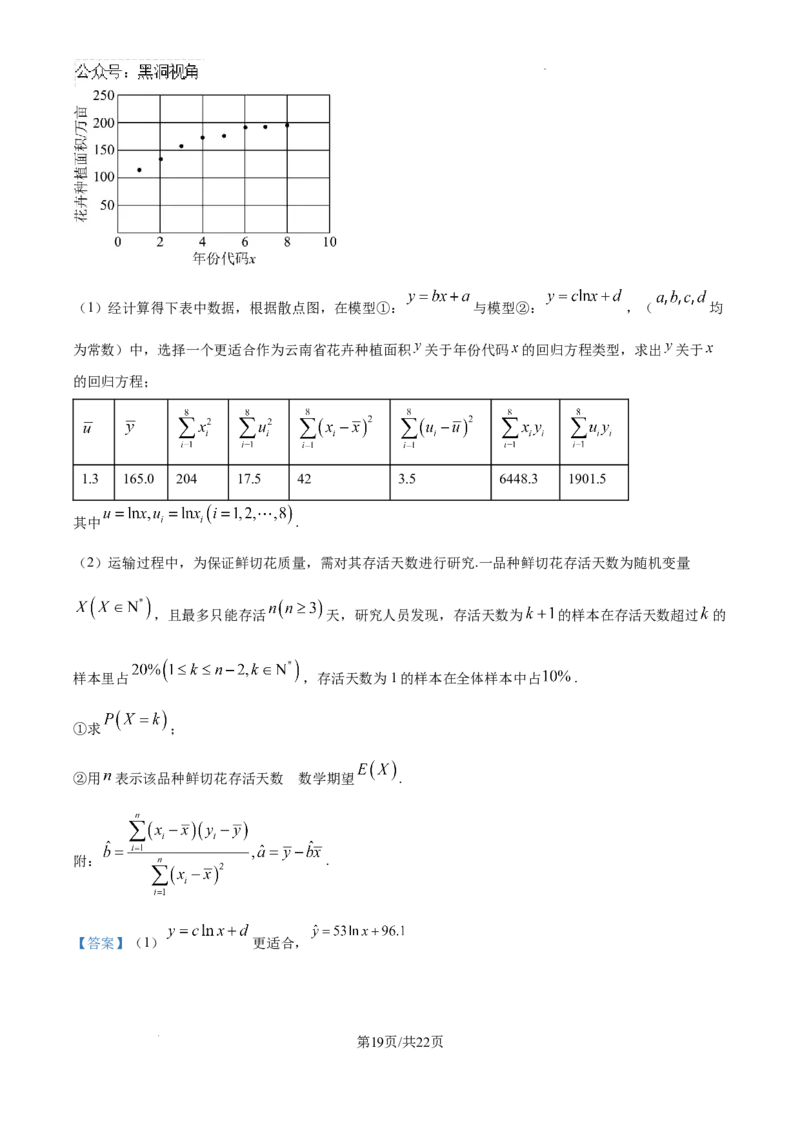
19. 云南花卉产业作为云南全力打造世界一流“绿色食品牌”的重点产业之一、从起步发展至今仅四十多年
的时间,取得了令人瞩目的成绩.目前云南已成为全球公认的三大最适宜鲜切花种植的区域之一,鲜切花种
植面积和产量位居全球第一,全省花卉种植面积稳定在190万亩左右.近8年云南省花卉种植面积统计数据
及散点图如图
第18页/共22页
学科网(北京)股份有限公司(1)经计算得下表中数据,根据散点图,在模型①: 与模型②: ,( 均
为常数)中,选择一个更适合作为云南省花卉种植面积 关于年份代码 的回归方程类型,求出 关于
的回归方程;
1.3 165.0 204 17.5 42 3.5 6448.3 1901.5
其中 .
(2)运输过程中,为保证鲜切花质量,需对其存活天数进行研究.一品种鲜切花存活天数为随机变量
,且最多只能存活 天,研究人员发现,存活天数为 的样本在存活天数超过 的
样本里占 ,存活天数为1的样本在全体样本中占 .
①求 ;
②用 表示该品种鲜切花存活天数 数的学期望 .
附: .
【答案】(1) 更适合,
第19页/共22页
学科网(北京)股份有限公司(2)① ;②
【解析】
【分析】(1)根据散点图,确定 更适合,再利用换元法,以及题中的数据,代入公式求回
归方程;
(2)①根据条件概率,以及递推关系,可证明数列 是以0.18为首项,0.8为公比的等比数列,
再根据分段函数的形式列出解析式;②根据①的结果,列式 ,再利用错位相减法,即可求解.
【小问1详解】
由散点图可知, 更适合作为云南省花卉种植面积y关于年份代码x的回归方程类型.
.
令 ,所以
因为 , , , ,
所以 .
所以 ,
所以 .
云南省花卉种植面积y关于年份代码x的回归方程为 .
【小问2详解】
①由题可得, ,
当 时, ,
第20页/共22页
学科网(北京)股份有限公司又 ,即 ,
同理可得,当 时, ,
两式相减得 ,
即 , , ,
因为 ,
所以,当 时, 是以0.18为首项,0.8为公比的等比数列,
当 时, ,
所以 .
②
,
令 ,
则 ,
两式相减得,
,
所以 ,
第21页/共22页
学科网(北京)股份有限公司则 .
【点睛】关键点点睛:本题的关键是由条件概率,以及公式 ,从
而列出数列 的递推关系式.
第22页/共22页
学科网(北京)股份有限公司