文档内容
成都石室中学 2023-2024 年度下期高 2024 届二诊模拟考试
数学试题(理)(A 卷)
(总分:150分,时间:120分钟 )
第Ⅰ卷(共60分)
一、选择题(本题共12道小题,每小题5分,共60分)
1
z=
1.已知复数 1+i(其中i为虚数单位),则z的虚部是
1 1 1 1
− − i i
2 2 2 2
A. B. C. D.
{ 1}
A={1,2},B= y|y=x2
2.若集合 ,则 a∈A 是a∈B的
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
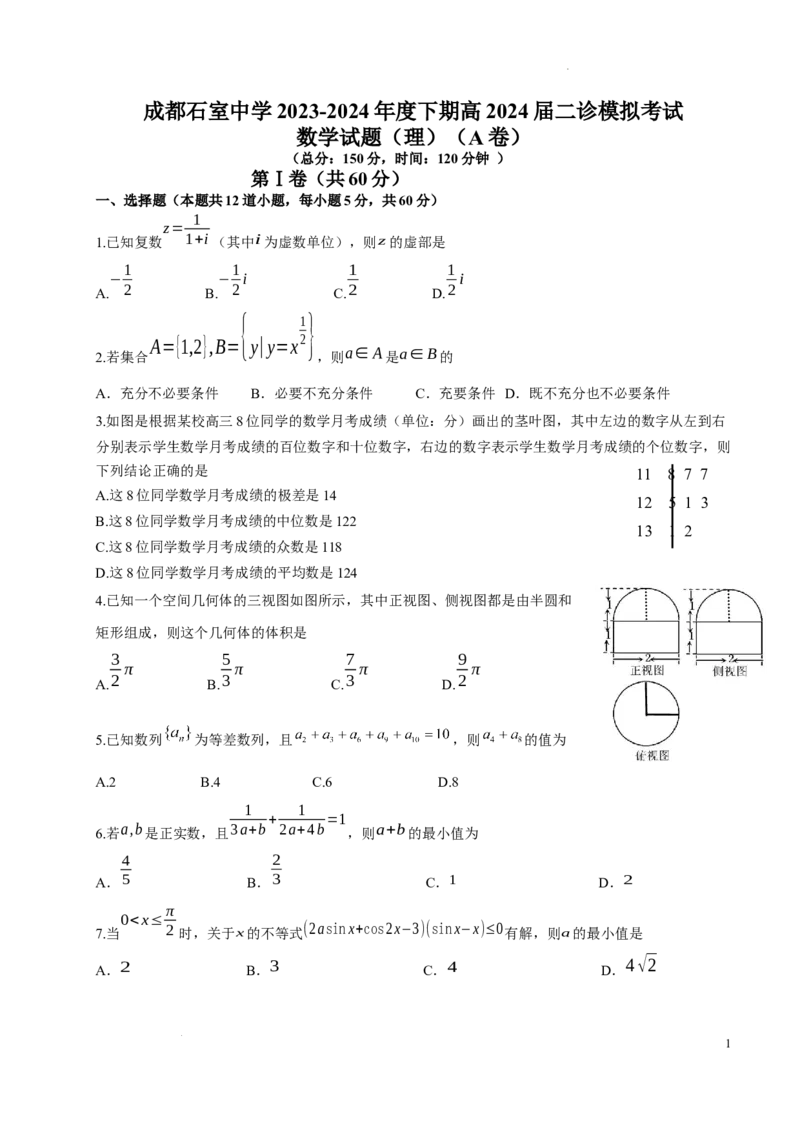
3.如图是根据某校高三8位同学的数学月考成绩(单位:分)画出的茎叶图,其中左边的数字从左到右
分别表示学生数学月考成绩的百位数字和十位数字,右边的数字表示学生数学月考成绩的个位数字,则
下列结论正确的是 11 8 7 7
A.这8位同学数学月考成绩的极差是14
12 5 1 3
B.这8位同学数学月考成绩的中位数是122
13 1 2
C.这8位同学数学月考成绩的众数是118
D.这8位同学数学月考成绩的平均数是124
4.已知一个空间几何体的三视图如图所示,其中正视图、侧视图都是由半圆和
矩形组成,则这个几何体的体积是
3 5 7 9
π π π π
2 3 3 2
A. B. C. D.
5.已知数列 为等差数列,且 ,则 的值为
A.2 B.4 C.6 D.8
1 1
+ =1
6.若 a,b 是正实数,且3a+b 2a+4b ,则a+b的最小值为
4 2
A.5 B.3 C.1 D.2
π
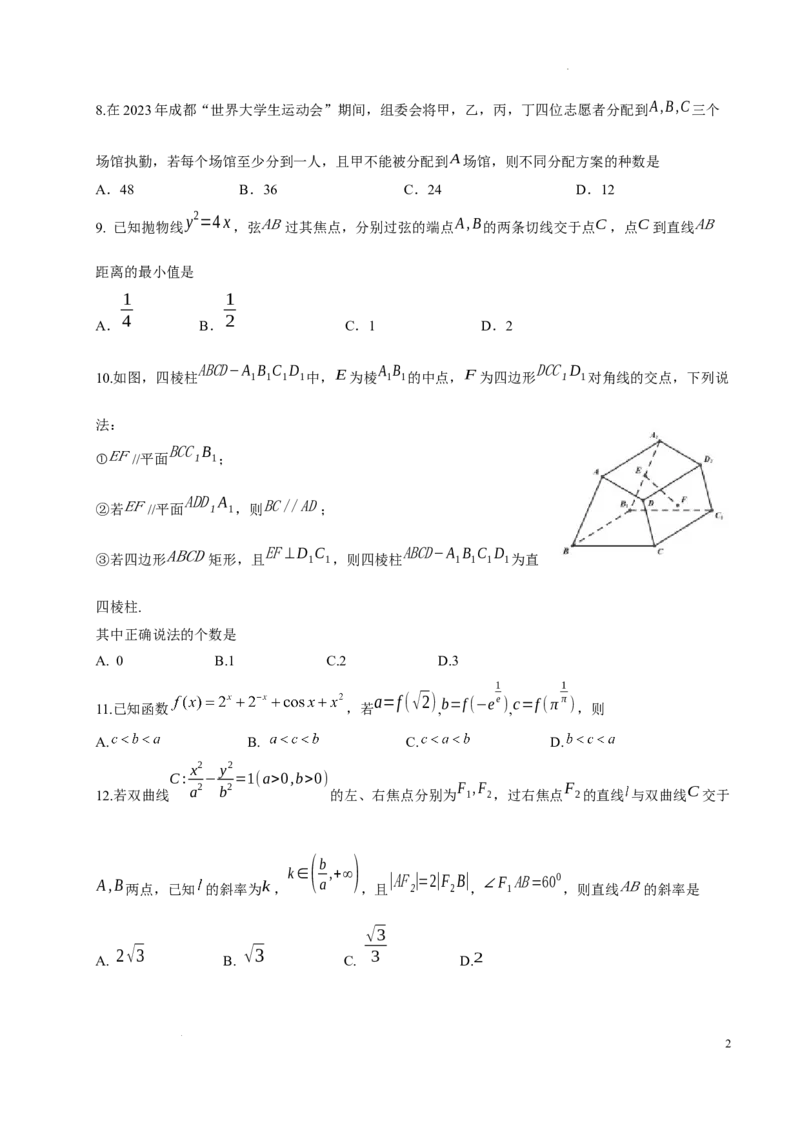
00,b>0)
12.若双曲线 a2 b2 的左、右焦点分别为 F 1 ,F 2,过右焦点 F 2的直线 与双曲线C交于
(b )
A,B 两点,已知 的斜率为k,
k∈
a
,+∞
,且 |AF 2 |=2|F 2 B| , ∠F 1 AB=600 ,则直线AB的斜率是
√3
A. 2√3 B. √3 C. 3 D.2
2
学科网(北京)股份有限公司第Ⅱ卷(共90分)
二、填空题(本题共4道小题,每小题5分,共20分)
13.已知向量
⃗a=(1,−2)
,
⃗b=(2,x)
,若
⃗a⊥ ⃗b
,则实数x= .
14.已知实数x,y满足约束条件 ,则 z=3x+2y 的最大值是 .
(1) n
S =x⋅ +27
n 3 a a ⋯a
15.已知等比数列 的前 项和为 ,若 ,则 1 2 n取最大值时,n的值为
.
x2 +1
ln ≤ex −x2 −mx−1
16.若 x≥1 ,恒有 ex −mx ,则m的取值范围是 .
三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。
17. (本小题满分12分)
为了去库存,某商场举行如下促销活动:有两个摸奖箱, 箱内有1个红球、1个黑球、8个白球, 箱
内有4个红球、4个黑球、2个白球,每次摸奖后放回.消费额满300元有一次 箱内摸奖机会,消费额
满600元有一次 箱内摸奖机会.每次机会均为从箱子中摸出1个球,中奖规则如下:红球奖50元代金券、
黑球奖30元代金券、白球奖10元代金券.
ξ
(Ⅰ)某三位顾客各有一次 箱内摸奖机会,求中奖10元代金券人数 的分布列;
(Ⅱ)某顾客消费额为600元,请问:这位顾客如何抽奖所得的代金券期望值较大?
18. (本小题满分12分)
f(x)=λ
已知 ,设 .
f(x)
(Ⅰ)求函数 的对称中心;
3
学科网(北京)股份有限公司2√3 √3
f(A)=
(Ⅱ)若ΔABC 中,角 A,B,C 所对的边分别为 a,b,c , 3 ,且ΔABC 外接圆的半径为 3 ,D
是 BC 边的中点,求线段AD长度的最大值.
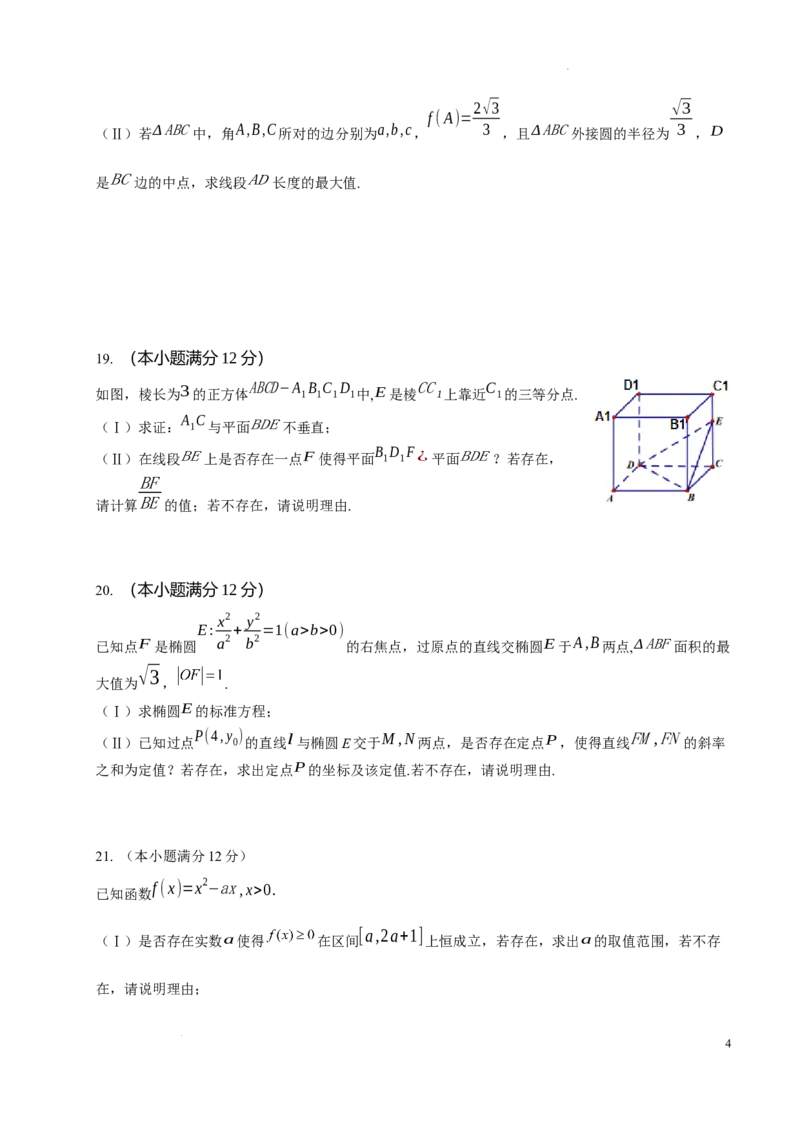
19. (本小题满分12分)
如图,棱长为 3 的正方体 ABCD−A 1 B 1 C 1 D 1中,E是棱 CC 1上靠近 C 1的三等分点.
A C
(Ⅰ)求证: 1 与平面BDE不垂直;
B D F
(Ⅱ)在线段BE上是否存在一点F使得平面
1 1
¿平面BDE?若存在,
BF
BE
请计算 的值;若不存在,请说明理由.
20. (本小题满分12分)
x2 y2
E: + =1(a>b>0)
已知点F是椭圆 a2 b2 的右焦点,过原点的直线交椭圆E于 A,B 两点,ΔABF面积的最
√3
大值为 , .
(Ⅰ)求椭圆E的标准方程;
(Ⅱ)已知过点 P(4,y 0 ) 的直线l与椭圆E交于 M,N 两点,是否存在定点P,使得直线 FM,FN 的斜率
之和为定值?若存在,求出定点P的坐标及该定值.若不存在,请说明理由.
21. (本小题满分12分)
已知函数
f(x)=x2 −ax,x>0.
[a,2a+1]
(Ⅰ)是否存在实数a使得 在区间 上恒成立,若存在,求出a的取值范围,若不存
在,请说明理由;
4
学科网(北京)股份有限公司h(x)=f(x)−a2lnx (1,ea
)
(Ⅱ)求函数 在区间 上的零点个数(e为自然对数的底数).
选考题:共10分。请考生在第22、23题中任选一题作答。如果多做,则按所做的第一题计分。
[选修4-4:坐标系与参数方程](10分)
22. (本小题满分10分)
(1,0)
在平面直角坐标系 中,倾斜角为α的直线 过定点 ,以 为极点, 轴的非负半轴为极轴建
ρsin2θ=4cosθ
立极坐标系,曲线 的极坐标方程为 ,直线 与曲线 相交于不同的两点 .
(Ⅰ)若 ,求线段 中点 的直角坐标;
(Ⅱ)若 ,求 的最小值.
[选修4-5:不等式选讲](10分)
23. (本小题满分10分)
f(x)=|x+1|
已知函数 .
f(x)+f(2x−1)