文档内容
公众号云儿和花
:
2024-2025 学年安徽省“卓越县中联盟&皖豫名校联盟”高二(上)期
中联考数学试题
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.在空间直角坐标系Oxyz中,与点A(4,−6,−1)关于Oxy平面对称的点的坐标为( )
A. (−4,−6,−1) B. (−4,6,−1) C. (4,−6,1) D. (4,6,1)
2.若直线ax+ y+1=0与(a+5)x+2y=0平行,则a=( )
A. 5 B. 4 C. 3 D. 2
3.已知△ABC的三个顶点分别为A(4,0),B(6,−7),C(4,−3),则BC边上的中线所在直线的方程是
( )
A. x+ y=0 B. x+ y−4=0 C. 5x+ y−12=0 D. 5x+ y−20=0
4.已知直线 恒过点 ,圆 ,则圆 上的点到直线 的距离的最大值为( )
l A(1,0) C:x2+(y−1) 2=4 C l
A. √2+3 B. √2+2 C. √2+1 D. √2
5.已知四面体 的所有棱长都等于 ,棱 , 的中点分别是 , ,则 ⃗ ⃗ ( )
ABCD a AB CD M N
AN⋅MC=
1 1 1
A. a2 B. a2 C. a2 D. a2
2 3 4
6.已知直线l过点B(−1,2,0)和C(0,3,1),则点A(1,1,2)到直线l的距离为( )
2√3 4√6
A. B. 2 C. √6 D.
3 3
7.已知椭圆 x2 y2 的右焦点为 ,过点 且斜率为 的直线与 交于 , 两点,若
C: + =1(a>b>0) F F 1 C A B
a2 b2
S =2S (O为坐标原点,S表示面积),则C的离心率为( )
△OAF △OBF
√3 √2 √3 √2
A. B. C. D.
2 2 3 3
8.在空间中,两两互相垂直且有公共原点的三条数轴构成空间直角坐标系,若任意两条数轴的夹角均为
60∘,我们将这种坐标系称为“斜60∘坐标系”.我们类比空间直角坐标系,定义“空间斜60∘坐标系”下向
量的斜60∘坐标:已知i⃗,⃗j,⃗k分别为“空间斜60∘坐标系”下三条数轴(x轴、y轴、z轴)正方向的单位向
⃗ ⃗ ⃗ ⃗
量,若向量 n=xi+ y j+zk ,则⃗n与有序实数组(x,y,z)相对应,称向量⃗n的斜60∘坐标为[x,y,z],记作
第 页,共 页
1 1公众号云儿和花
:
⃗ n=[x,y,z].如图,在平行六面体ABCD−A
1
B
1
C
1
D
1
中,AB=AD=2,A A
1
=4,
⃗ ⃗ ⃗
∠BAD=∠BA A
1
=∠DA A
1
=60∘,以
{AB,AD,A A }
为基底建立“空间斜60∘坐标系”,若
1
⃗ ⃗
AM=[2,t,0] ,且⃗AM与AC 的夹角为90∘,则t=( )
1
A. −√2
B. −2
C. √2
D. 2
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.已知平面 , 的法向量分别是⃗ ,⃗ ,直线 的方向向量为⃗ ,则( )
α β m=(2,−1,2) n=(2,4,0) l a=(1,4,1)
A. α⊥β B. l//α
C. ⃗ ⃗ ⃗ 可以作为空间的一个基底 D. 在 上的投影向量的模长为
{a,m,n}
⃗n ⃗a 3√2
x2
10.已知椭圆C: + y2=1的左、右焦点分别为F ,F ,P是C上一点,若△F PF 是直角三角形,则
2 1 2 1 2
△F PF 的面积可以是( )
1 2
1 √2 √3
A. B. C. D. 1
2 2 2
1
11.已知点A(0,2),B(0, ),曲线C 是满足|MA|=2|MB|的点M的轨迹,P,Q分别是曲线C 与圆
2 1 1
上的动点,则下列说法正确的是( )
C :(x−3) 2+(y+4) 2=r2 (r>0)
2
A. 若曲线C 与圆C 有公共点,则4≤r≤6
1 2
B. 若r=2√3,则两曲线交点所在直线的方程为3x−4 y−7=0
C. 若r=3,则|PQ|的取值范围为[1,9]
π
D. 若r=2,过点P作圆C 的两条切线,切点分别为E,F,则存在点P,使得∠EPF=
2 2
三、填空题:本题共3小题,每小题5分,共15分。
12.圆C:x2+ y2−2ax−4ay+4a2+2a−3=0的半径的最小值为 .
第 页,共 页
2 1公众号云儿和花
:
13.已知椭圆 x2 y2 的左、右焦点分别为 , ,过点 的直线与 交于 , 两点,则
C: + =1(a>b>0) F F F C A B
a2 b2 1 2 2
A,B,F 三点能构成边长为4的正三角形时,C的方程为 .
1
⃗ ⃗
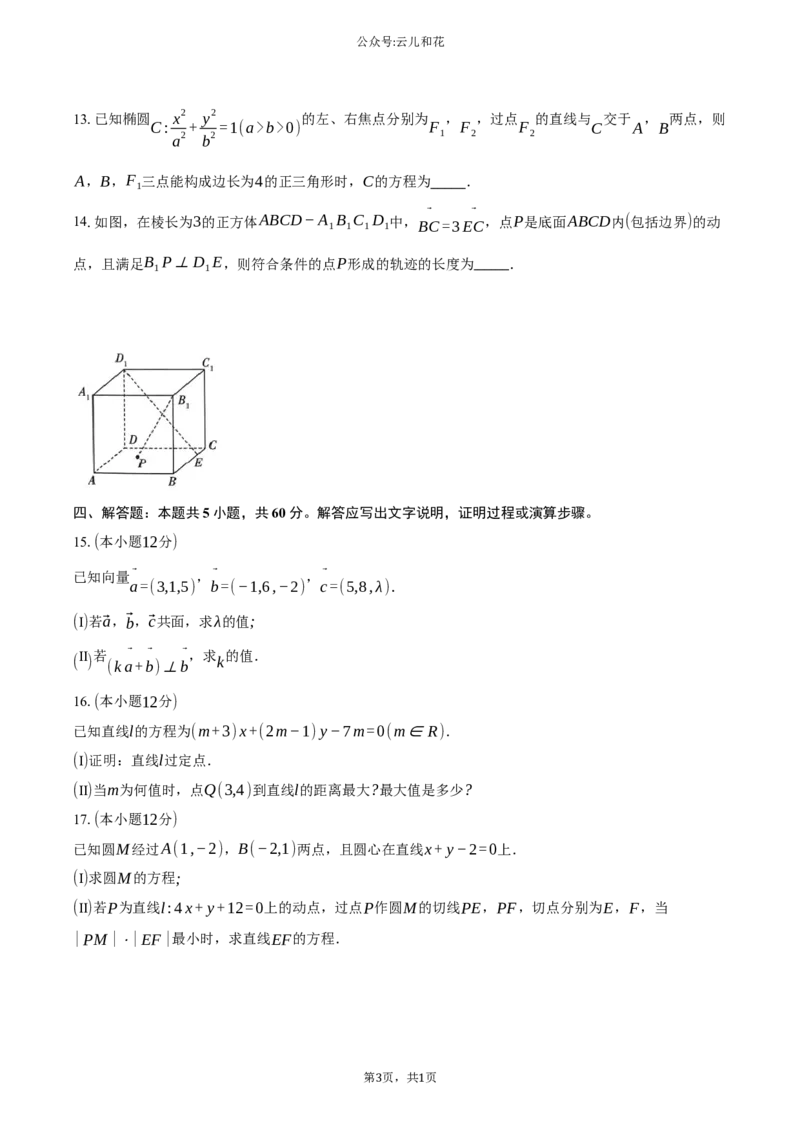
14.如图,在棱长为3的正方体ABCD−A 1 B 1 C 1 D 1 中, BC=3EC ,点P是底面ABCD内(包括边界)的动
点,且满足B P⊥D E,则符合条件的点P形成的轨迹的长度为 .
1 1
四、解答题:本题共5小题,共60分。解答应写出文字说明,证明过程或演算步骤。
15.(本小题12分)
已知向量⃗ ,⃗ ,⃗
a=(3,1,5) b=(−1,6,−2) c=(5,8,λ).
(Ⅰ)若⃗a,⃗b,⃗c共面,求λ的值;
Ⅱ 若 ⃗ ⃗ ⃗,求 的值.
( ) (ka+b)⊥b k
16.(本小题12分)
已知直线l的方程为(m+3)x+(2m−1)y−7m=0(m∈R).
(Ⅰ)证明:直线l过定点.
(Ⅱ)当m为何值时,点Q(3,4)到直线l的距离最大?最大值是多少?
17.(本小题12分)
已知圆M经过A(1,−2),B(−2,1)两点,且圆心在直线x+ y−2=0上.
(Ⅰ)求圆M的方程;
(Ⅱ)若P为直线l:4x+ y+12=0上的动点,过点P作圆M的切线PE,PF,切点分别为E,F,当
|PM|⋅|EF|最小时,求直线EF的方程.
第 页,共 页
3 1公众号云儿和花
:
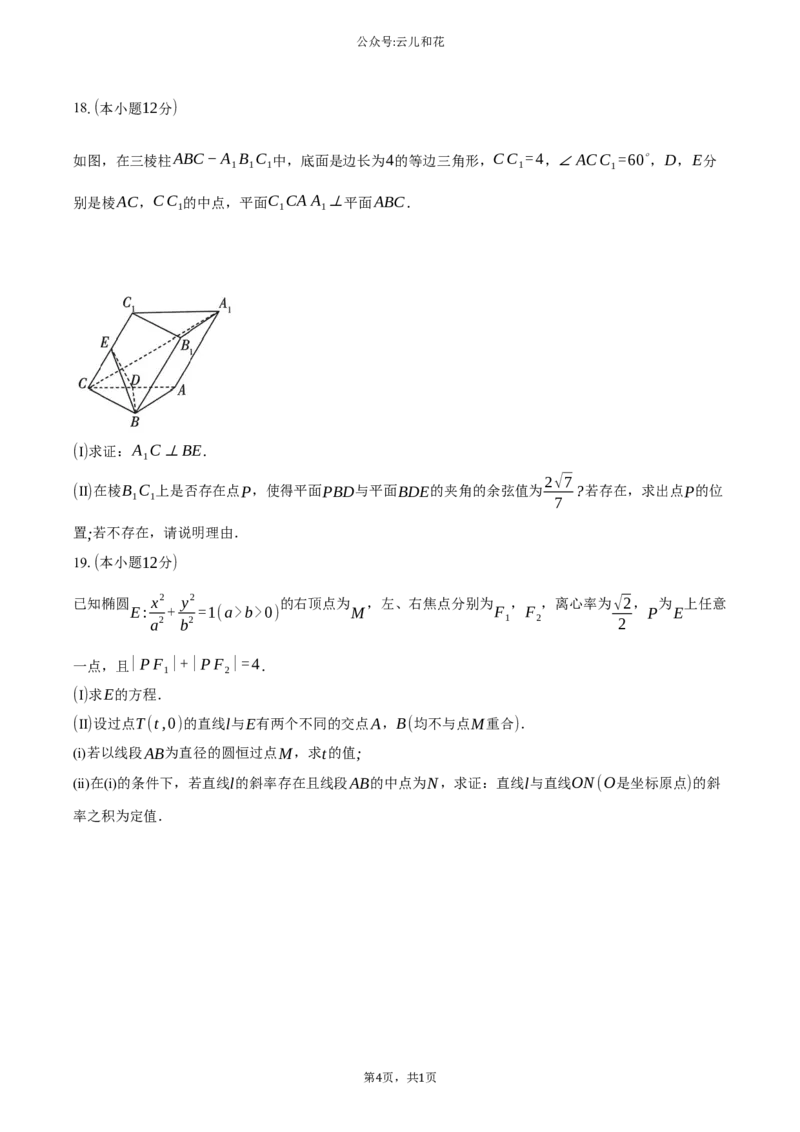
18.(本小题12分)
如图,在三棱柱ABC−A B C 中,底面是边长为4的等边三角形,CC =4,∠ACC =60∘,D,E分
1 1 1 1 1
别是棱AC,CC 的中点,平面C CA A ⊥平面ABC.
1 1 1
(Ⅰ)求证:A C⊥BE.
1
2√7
(Ⅱ)在棱B C 上是否存在点P,使得平面PBD与平面BDE的夹角的余弦值为 ?若存在,求出点P的位
1 1 7
置;若不存在,请说明理由.
19.(本小题12分)
已知椭圆 x2 y2 的右顶点为 ,左、右焦点分别为 , ,离心率为√2, 为 上任意
E: + =1(a>b>0) M F F P E
a2 b2 1 2 2
一点,且|PF |+|PF |=4.
1 2
(Ⅰ)求E的方程.
(Ⅱ)设过点T(t,0)的直线l与E有两个不同的交点A,B(均不与点M重合).
(ⅰ)若以线段AB为直径的圆恒过点M,求t的值;
(ⅱ)在(ⅰ)的条件下,若直线l的斜率存在且线段AB的中点为N,求证:直线l与直线ON(O是坐标原点)的斜
率之积为定值.
第 页,共 页
4 1公众号云儿和花
:
参考答案
1.C
2.A
3.D
4.B
5.B
6.C
7.D
8.B
9.ACD
10.BD
11.AC
12.√2
x2 y2
13. + =1
9 6
14.√10
15.解: Ⅰ , ,
( )∵⃗a=(3,1,5) ⃗b=(−1,6,−2)
∴⃗a与⃗b不平行,
∵⃗a,⃗b,⃗c共面,
{3x−y=5,
∴存在实数x,y,使得⃗c=x⃗a+ y⃗b,即 x+6 y=8,
5x−2y=λ,
{x=2,
解得 y=1,
λ=8,
故实数λ的值为8.
Ⅱ , ,且 ,
( )∵⃗a=(3,1,5) ⃗b=(−1,6,−2) (k⃗a+⃗b)⊥⃗b
第 页,共 页
5 1公众号云儿和花
:
⃗ ,
∴(k⃗a+⃗b)⋅⃗b=k⃗a⋅⃗b+b2=0
41
即k(−3+6−10)+(1+36+4)=0,解得k= .
7
16.解:(Ⅰ)将直线l的方程整理得(x+2y−7)m+(3x−y)=0,
{x+2y−7=0, {x=1,
由 解得
3x−y=0, y=3,
所以直线l恒过点(1,3);
(Ⅱ)由(Ⅰ)可得直线l过定点,设定点为P(1,3),
当 时,点 到直线 的距离最大,且最大距离 ,
PQ⊥l Q l d=|PQ|=√(1−3) 2+(3−4) 2=√5
即点Q到直线l的最大距离为√5,
4−3 1 m+3
此时k = = ,而直线l的斜率k=− ,
PQ 3−1 2 2m−1
m+3 5
所以− =−2,解得m= .
2m−1 3
17.解: Ⅰ 设圆 的标准方程为 ,
( ) M (x−a) 2+(y−b) 2=r2 (r>0)
{(1−a) 2+(−2−b) 2=r2 {a=1
由已知得 ,解得
(−2−a) 2+(1−b) 2=r2 b=1,
a+b−2=0 r=3
所以圆 的方程为 .
M (x−1) 2+(y−1) 2=9
Ⅱ 由 Ⅰ 知圆 的方程为 ,圆心为 ,半径 .
( ) ( ) M (x−1) 2+(y−1) 2=9 M(1,1) r=3
1
因为S = |PM|⋅|EF|=2S =|PE|⋅|EM|=3|PE|=3√|PM|2−9,
四 边 形PEM2F △PEM
所以要使|PM|⋅|EF|最小,则需|PM|最小,此时PM与直线l垂直,
第 页,共 页
6 1公众号云儿和花
:
1
由直线l:4x+ y+12=0,可得直线PM的斜率为 ,
4
1
直线PM的方程为y−1= (x−1),即x−4 y+3=0,
4
{x−4 y+3=0, {x=−3,
由 解得 即P(−3,0),
4x+ y+12=0, y=0,
1 17
则以PM为直径的圆的方程为(x+1) 2+(y− ) 2= .
2 4
{ (x−1) 2+(y−1) 2=9
由 两式相减可得直线 的方程为 .
1 17 , EF 4x+ y+4=0
(x+1) 2+(y− ) 2=
2 4
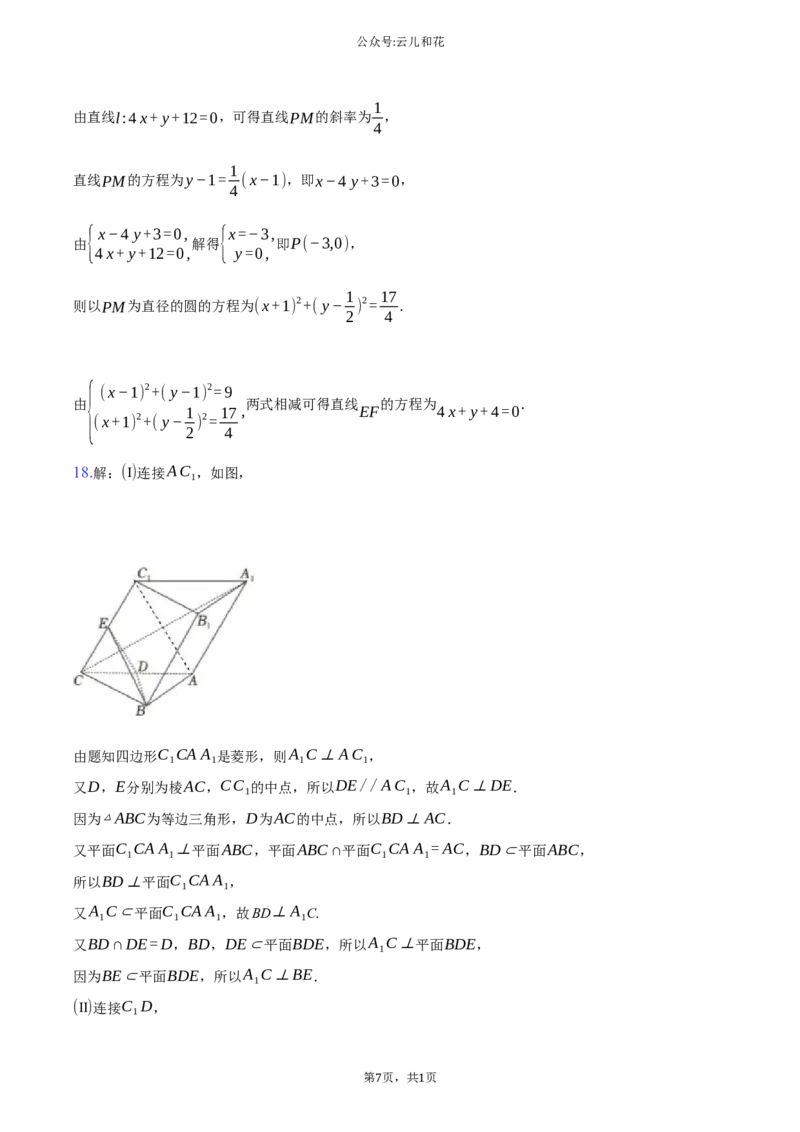
18.解:(Ⅰ)连接AC ,如图,
1
由题知四边形C CA A 是菱形,则A C⊥AC ,
1 1 1 1
又D,E分别为棱AC,CC 的中点,所以DE//AC ,故A C⊥DE.
1 1 1
因为△ABC为等边三角形,D为AC的中点,所以BD⊥AC.
又平面C CA A ⊥平面ABC,平面ABC∩平面C CA A =AC,BD⊂平面ABC,
1 1 1 1
所以BD⊥平面C CA A ,
1 1
又A C⊂平面C CA A ,故BD⊥A C.
1 1 1 1
又BD∩DE=D,BD,DE⊂平面BDE,所以A C⊥平面BDE,
1
因为BE⊂平面BDE,所以A C⊥BE.
1
(Ⅱ)连接C D,
1
第 页,共 页
7 1公众号云儿和花
:
由AC=CC =4,∠ACC =60∘,可知△C CA为等边三角形,
1 1 1
又D是AC的中点,所以C D⊥AC,
1
由(Ⅰ)得BD⊥平面C CA A ,所以DB,DA,DC 两两互相垂直.
1 1 1
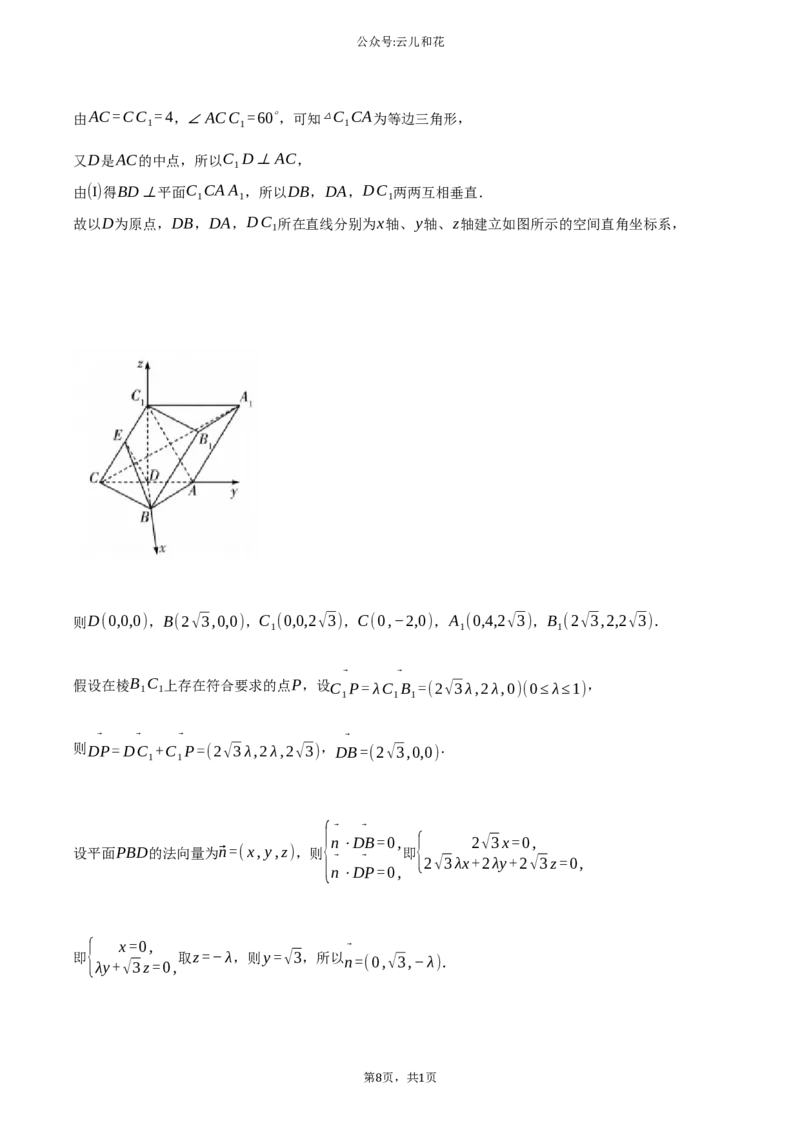
故以D为原点,DB,DA,DC 所在直线分别为x轴、y轴、z轴建立如图所示的空间直角坐标系,
1
则D(0,0,0),B(2√3,0,0),C (0,0,2√3),C(0,−2,0),A (0,4,2√3),B (2√3,2,2√3).
1 1 1
⃗ ⃗
假设在棱B 1 C 1 上存在符合要求的点P,设C P=λC B =(2√3λ,2λ,0)(0≤λ≤1) ,
1 1 1
⃗ ⃗ ⃗ ⃗
则DP=DC +C P=(2√3λ,2λ,2√3) ,DB=(2√3,0,0) .
1 1
{⃗ ⃗
n⋅DB=0, { 2√3x=0,
设平面PBD的法向量为⃗n=(x,y,z),则 即
⃗ ⃗ 2√3λx+2λy+2√3z=0,
n⋅DP=0,
{ x=0, ⃗
即
λy+√3z=0,
取z=−λ,则y=√3,所以n=(0,√3,−λ).
第 页,共 页
8 1公众号云儿和花
:
⃗ ⃗
由(Ⅰ)得m=C A =(0,6,2√3) 是平面BDE的一个法向量,
1
2√7
因为平面PBD与平面BDE的夹角的余弦值为 ,
7
⃗ |6√3−2√3λ| |3−λ| 2√7 1
所以|cos<⃗m,n>|= = = ,即3λ2+14λ−5=0,解得λ= 或λ=−5(舍去
4√3×√λ2+3 2√λ2+3 7 3
),
故存在点P,且P为棱C B 上靠近点C 的一个三等分点,使得平面PBD与平面BDE的夹角的余弦值为
1 1 1
2√7
.
7
19.解:(Ⅰ)设椭圆E的半焦距为c(c>0).
由题意得2a=4,a=2.
c √2
因为E的离心率e= = ,所以c=√2,结合a2−c2=b2,得b=√2,
a 2
x2 y2
所以E的方程为 + =1.
4 2
(II)(i)设直线l的方程为x=my+t,A(x ,y ),B(x ,y ),
1 1 2 2
由{ x=my+t, 消去 ,得 ,
x (m2+2)y2+2mty+t2−4=0
x2+2y2−4=0
所以 , 2mt , t2−4,
Δ=(2mt) 2−4(m2+2)(t2−4)=8(2m2−t2+4)>0 y + y =− y y =
1 2 m2+2 1 2 m2+2
4t
所以x +x =m(y + y )+2t= ,
1 2 1 2 m2+2
m2 (t2−4) 2m2t2 2t2−4m2,
x x =(my +t)(my +t)=m2y y +mt(y + y )+t2= − +t2=
1 2 1 2 1 2 1 2 m2+2 m2+2 m2+2
因为以线段AB为直径的圆恒过点M(2,0),
第 页,共 页
9 1公众号云儿和花
:
所以
M
⃗
A⋅M
⃗
B=0
,即 (x
1
−2)(x
2
−2)+ y
1
y
2
=0 ,
所以 ,即2t2−4m2 4t t2−4 ,
x x −2(x +x )+4+ y y =0 −2× +4+ =0
1 2 1 2 1 2 m2+2 m2+2 m2+2
2 2
即3t2−8t+4=0,解得t= 或t=2(舍去),满足Δ>0,故t= .
3 3
(ii)由题可知m≠0.
8 4m 4 2m
结合(i)可知x +x = ,y + y =− ,所以N( ,− ),
1 2 3(m2+2) 1 2 3(m2+2) 3(m2+2) 3(m2+2)
2m
−
所以直线 的斜率
3(m2+2)
m,
ON k = =−
ON 4 2
3(m2+2)
1 1 m 1
又直线l的斜率k = ,所以k ⋅k = ⋅(− )=− ,为定值,证毕.
AB m AB ON m 2 2
第 页,共 页
10 1