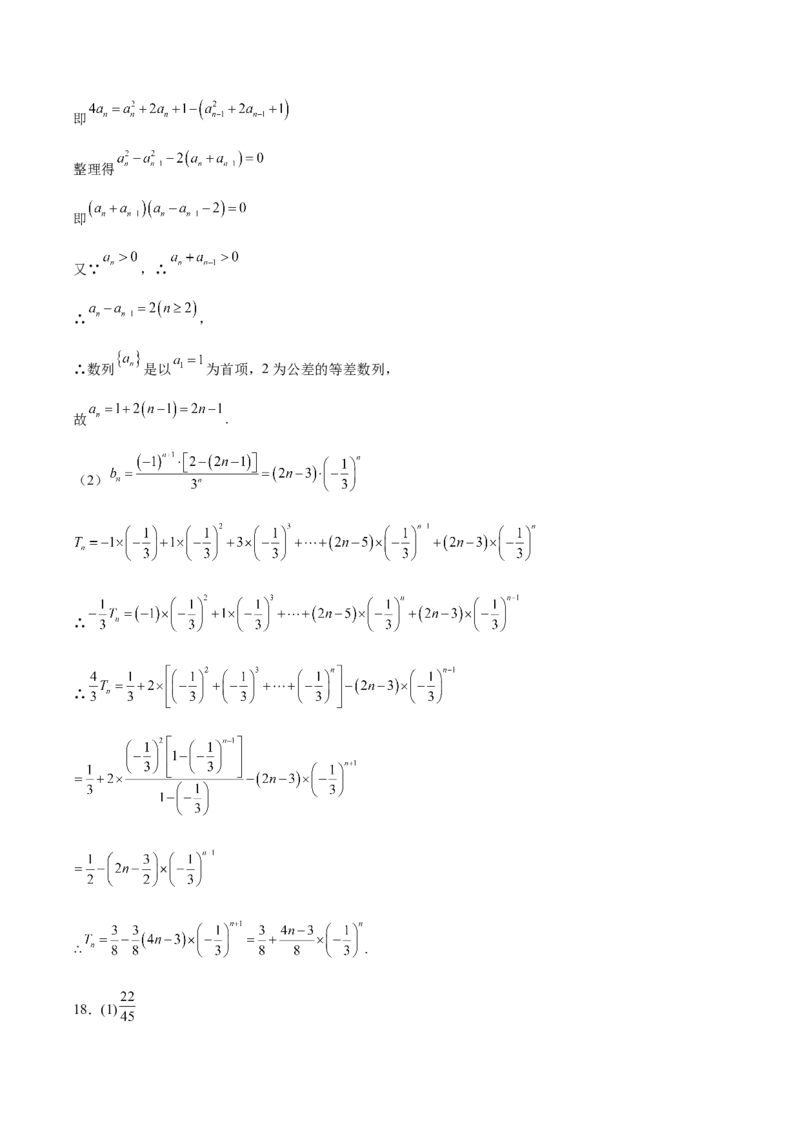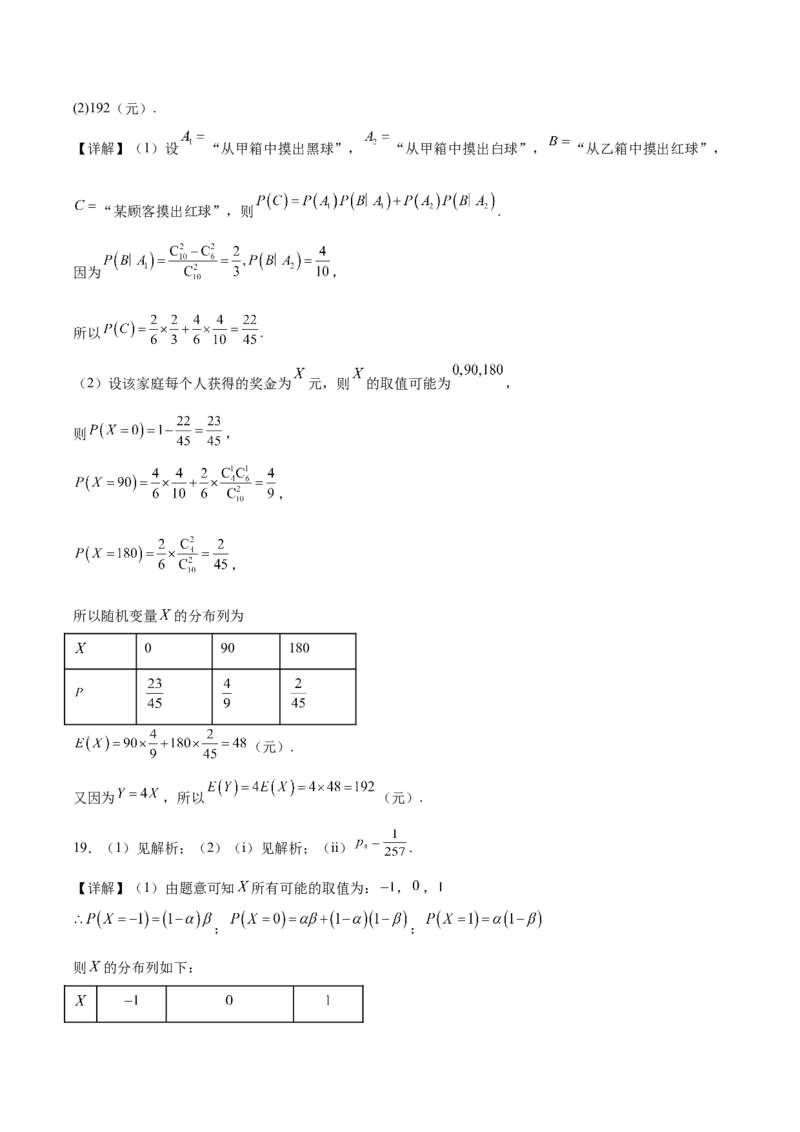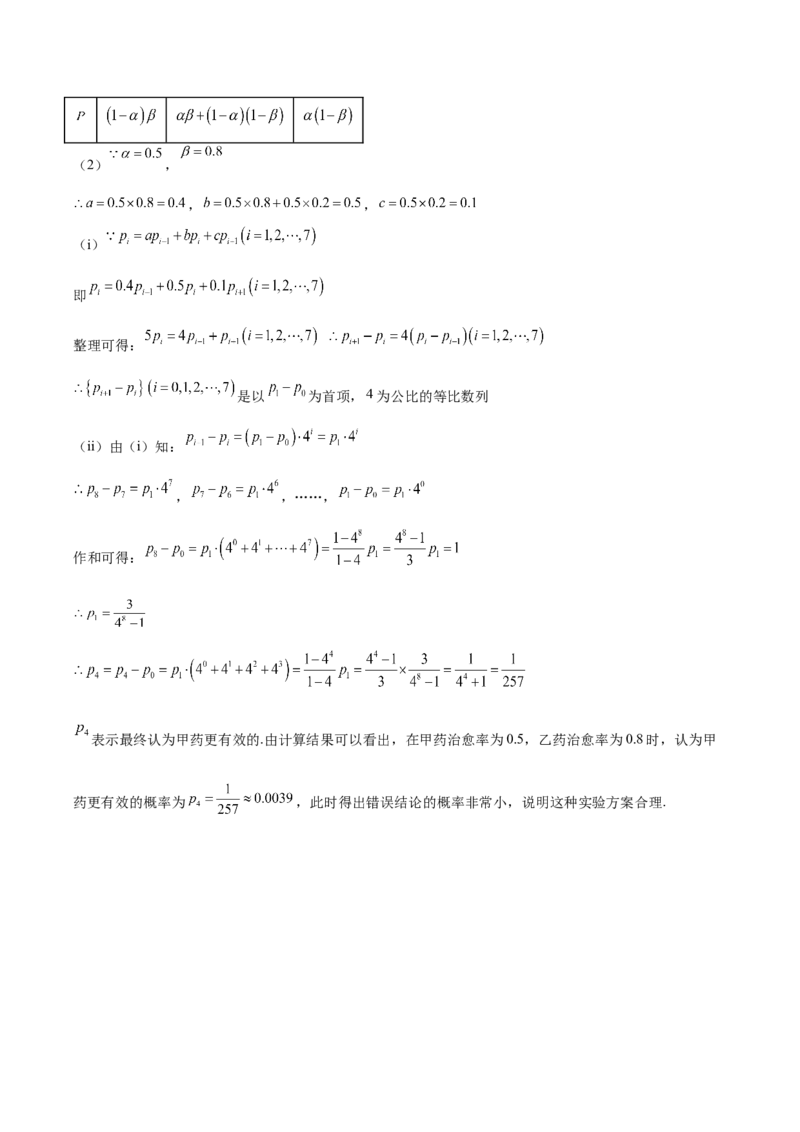文档内容
山东省潍坊第一中学2024-2025学年高二下学期第二次质量检测数学试题
一、单选题
1.某企业建立了风险分级管控和隐患排查治理的双重独立预防机制,已知两套机制失效的概率分别为
和 ,则恰有一套机制失效的概率为( )
A. B. C. D.
2.已知随机变量 服从正态分布 , ,则 ( )
A.0.2 B.0.3 C.0.7 D.0.8
3.若数列 的通项公式为 ,则 ( )
A.27 B.21 C.15 D.13
4.有10件产品,其中3件是次品,从中不放回地任取2件,若X表示取得次品的件数,则
( )
A. B. C. D.1
5.如图给出一个“直角三角形数阵”满足每一列的数成等差数列,从第三行起,每一行的数成等比数列,
且每一行的公比相等,则第8行第3列的数为( )
A. B. C. D.1
6.某次考试共有12个选择题,每个选择题的分值为5分,每个选择题四个选项且只有一个选项是正确的,
学生对12个选择题中每个题的四个选择项都没有把握,最后选择题的得分为 分, 学生对12个选择题中每个题的四个选项都能判断其中有一个选项是错误的,对其它三个选项都没有把握,选择题的得分为
分,则 的值为
A. B. C. D.
7.等比数列 的各项均为正数,且 .设 ,则数列
的前项和 ( )
A. B. C. D.
8.甲、乙两人进行一场游戏比赛,其规则如下:每一轮两人分别投掷一枚质地均匀的骰子,比较两者的
点数大小,其中点数大的得3分,点数小的得0分,点数相同时各得1分.经过三轮比赛,在甲至少有一
轮比赛得3分的条件下,乙也至少有一轮比赛得3分的概率为( )
A. B. C. D.
二、多选题
9.已知随机变量 ,且 ,则下列说法正确的是( )
A. B.
C. D.
10.已知 是等差数列, 是其前 项和,则下列命题为真命题的是( )
A.若 ,则
B.若 ,则
C.若 ,则D.若 和 都为递增数列,则
11.爆竹声声辞旧岁,银花朵朵贺新春.除夕夜里小光用3D投影为家人进行虚拟现实表演,表演分为
“燃爆竹、放烟花、辞旧岁、迎新春”4个环节.小光按照以上4个环节的先后顺序进行表演,每个环节
表演一次.假设各环节是否表演成功互不影响,若每个环节表演成功的概率均为 ,则( )
A.事件“成功表演燃爆竹环节”与事件“成功表演辞旧岁环节”互斥
B.“放烟花”、“迎新春”环节均表演成功的概率为
C.表演成功的环节个数的期望为3
D.在表演成功的环节恰为3个的条件下“迎新春”环节表演成功的概率为
三、填空题
12.古希腊数学家把数1,3,6,10,15,21,…叫做三角形数,三角形数中蕴含一定的规律性,则第
2025个三角形数与第2024个三角形数的差为 .
13.在某市 年 月的高二质量检测考试中,理科学生的数学成绩服从正态分布 .已知参加本
次考试的全市理科学生约 人.某学生在这次考试中的数学成绩是 分,那么他的数学成绩大约排在
全市第 名.
(参考数值: , ,
)
14.已知函数 满足 ,则满足
的最大正整数 的值为 .
四、解答题
15.已知数列 的前 项和 ,
(1)求数列 的通项公式;
(2)求数列 的前多少项和最大.16.随着全球经济一体化进程的不断加快,机械零件的加工质量决定了制造工厂的生存,零件加工精度逐
渐成为供应商判断制造公司产品的标准.已知某公司生产不同规格的一种产品,根据检测精度的标准,其合
格产品的质量y( )与尺寸x( )之间近似满足关系式 (b,c为大于0的常数).现随机从中
抽取6件合格产品,测得数据如下:
尺寸x( 〕 38 48 58 68 78 88
质量y( 〕 16.8 18.8 20.7 22.4 24 25.5
根据测得数据作出如下处理:令 ,得相关统计量的值如下表:
75.3 24.6 18.3 101.4
(1)根据所给统计数据,求y关于x的回归方程;
(2)若从一批该产品中抽取n件进行检测,已知检测结果的误差 满足 ,求至少需要抽取多少
件该产品,才能使误差 在(-0.1,0.1)的概率不少于0.9545?
附:①对于样本 , i)(i=1,2,…,n),其回归直线 的斜率和截距的最小二乘估计公式分
别为: , , .② ,则
17.在数列 中, , 是其前n项和,且 .
(1)求数列 的通项公式;
(2)设 ,求数列 的前n项和 .
18.某商场举行抽奖活动,准备了甲、乙两个箱子,甲箱内有2个黑球、4个白球,乙箱内有4个红球、6个黄球.每位顾客可参与一次抽奖,先从甲箱中摸出一个球,如果是黑球,就可以到乙箱中一次性地摸出两个
球;如果是白球,就只能到乙箱中摸出一个球.摸出一个红球可获得90元奖金,摸出两个红球可获得180
元奖金.
(1)求某顾客摸出红球的概率;
(2)设某家庭四人均参与了抽奖,他们获得的奖金总数为 元,求随机变量 的数学期望 .
19.为了治疗某种疾病,研制了甲、乙两种新药,希望知道哪种新药更有效,为此进行动物试验.试验方
案如下:每一轮选取两只白鼠对药效进行对比试验.对于两只白鼠,随机选一只施以甲药,另一只施以乙
药.一轮的治疗结果得出后,再安排下一轮试验.当其中一种药治愈的白鼠比另一种药治愈的白鼠多4只
时,就停止试验,并认为治愈只数多的药更有效.为了方便描述问题,约定:对于每轮试验,若施以甲药
的白鼠治愈且施以乙药的白鼠未治愈则甲药得1分,乙药得 分;若施以乙药的白鼠治愈且施以甲药的白
鼠未治愈则乙药得1分,甲药得 分;若都治愈或都未治愈则两种药均得0分.甲、乙两种药的治愈率分
别记为α和β,一轮试验中甲药的得分记为X.
(1)求 的分布列;
(2)若甲药、乙药在试验开始时都赋予4分, 表示“甲药的累计得分为 时,最终认为甲药
比乙药更有效”的概率,则 , , ,其中 ,
, .假设 , .
(i)证明: 为等比数列;
(ii)求 ,并根据 的值解释这种试验方案的合理性.题号 1 2 3 4 5 6 7 8 9 10
答案 C A A C C A B B ABD BC
题号 11
答案 BCD
12.2025
分析两项之差并归纳结果可以得到答案.
【详解】
设三角数从最开始的数为 第 个数为
归纳可知 ,所以 .
故答案为:2025.
13.
分析可得 ,计算得出 的概率,乘以 可得结果.
【详解】 考试的成绩 服从正态分布 ,所以, , ,
所以, ,则 ,
数学成绩为 分的学生大约排在全市第 名.
故答案为: .
14.12
根据递推关系可得 是公比为2的等比数列,即可求解通项,进而根据等比求和将问题转化为
,根据不等式求解即可.
【详解】 ,
所以数列 是公比为2的等比数列,所以所解不等式为:
当 时,则 ,
可解得:
的最大值为12,
当 时, 符合要求,
当 时, 不符合要求,
因此 的最大值为12,
故答案为:12
15.(1) (2) 前16项的和最大
(1)利用 时, 可求得通项公式;
(2)利用二次函数的解析式配方可得答案.
【详解】解:(1)当 时, ;当 时,
;
所以: ;
(2)因为 ;
所以前16项的和最大.
16.(1)
(2)800(1)按照公式求出 与 ,写出回归方程;(2)根据正态分布及所给数据得出不等关系 ,解出
答案.
【详解】(1) , ,所以
,即 ,整理为: ,所以y关于x的回归方程为
(2)因为 , ,所以 ,要想使误差 在
(-0.1,0.1)的概率不少于0.9545,则满足 ,解得: ,即至少需要抽取800件该产品,才
能使误差 在(-0.1,0.1)的概率不少于0.9545.
17.(1)
(2)
(1)利用 与 的关系推理得到 ,利用等差数列定义求解即得;
(2)利用错位相减法求得数列 的前n项和 即可.
【详解】(1)由 ,可得 ①,
当 时, ,解得 ,
当 时, ②,
由①-②:即
整理得
即
又∵ ,∴
∴ ,
∴数列 是以 为首项,2为公差的等差数列,
故 .
(2)
∴
∴
∴ .
18.(1)(2)192(元).
【详解】(1)设 “从甲箱中摸出黑球”, “从甲箱中摸出白球”, “从乙箱中摸出红球”,
“某顾客摸出红球”,则 .
因为 ,
所以 .
(2)设该家庭每个人获得的奖金为 元,则 的取值可能为 ,
则 ,
,
,
所以随机变量 的分布列为
0 90 180
(元).
又因为 ,所以 (元).
19.(1)见解析;(2)(i)见解析;(ii) .
【详解】(1)由题意可知 所有可能的取值为: , ,
; ;
则 的分布列如下:(2) ,
, ,
(i)
即
整理可得:
是以 为首项, 为公比的等比数列
(ii)由(i)知:
, ,……,
作和可得:
表示最终认为甲药更有效的.由计算结果可以看出,在甲药治愈率为0.5,乙药治愈率为0.8时,认为甲
药更有效的概率为 ,此时得出错误结论的概率非常小,说明这种实验方案合理.