数学-2024届高三11月大联考（新课标II卷）（辽宁专用）（全解全析及评分标准）_2023年11月_01每日更新_13号_2024届辽宁省高三11月半期大联考（辽宁专用）

2024 届高三 11 月大联考（新课标 II 卷）（辽宁专用） 数学·全解全析及评分标准 1 2 3 4 5 6 7 8 9 10 11 12 B C A B D C B D BD ABD ACD CD 一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一个选项是符合题 目要求的。 1．B 【解析】解不等式 (x2)(x1)0 ，得 1 x2 ，所以集合 A(1,2) .又 x2 33 ，所以 ylog (x2 3)log 31，所以集合B[1,)，所以A  B[1,2).故选B． 3 3 2．C 【解析】由a2 a a ，知当a 0时，数列{a }不是等比数列；反之，当数列{a }为等比数列时， n1 n n2 n n n 必有a2 a a ，所以“a2 a a (nN*)”是“数列{a }为等比数列”的必要不充分条件.故选C． n1 n n2 n1 n n2 n   5 3．A 【解析】由题意，得 f( )1，所以 2k,kZ，所以 2k,kZ.又0，所 3 6 6 5 以 ．故选A． 6 4．B 【解析】设ux(ax)，因为yeu在定义域内是增函数，所以ux(ax)在(1,2)上单调递增，所以 a 2，所以a4.故选B． 2 5．D 【解析】由题意，知sinCcosC7sin(AB)7sinC，所以cosC6sinC．又sin2Ccos2C1， 37 4 37 0C π，所以sinC  ，所以由正弦定理，得AB2RsinC (R为△ABC外接圆的半径).故 37 37 选D． 6．C【解析】如图，连接AC,PC．   因为正方形ABCD的边长为 2 ，点P在边AD上，所以设APAD，其中01，                   所以AP(ACPC) APAC APPC  APAC AP(PDDC) APAC APPD+APDC     2 |AD||AC|cos45(1)|AD||AD|0 22 2(1) 2 22 42(1)2 22，    当1，即P点与D点重合时，等号成立，故AP(ACPC)的最大值为2．故选C． 数学 全解全析及评分标准 第1页（共11页） {#{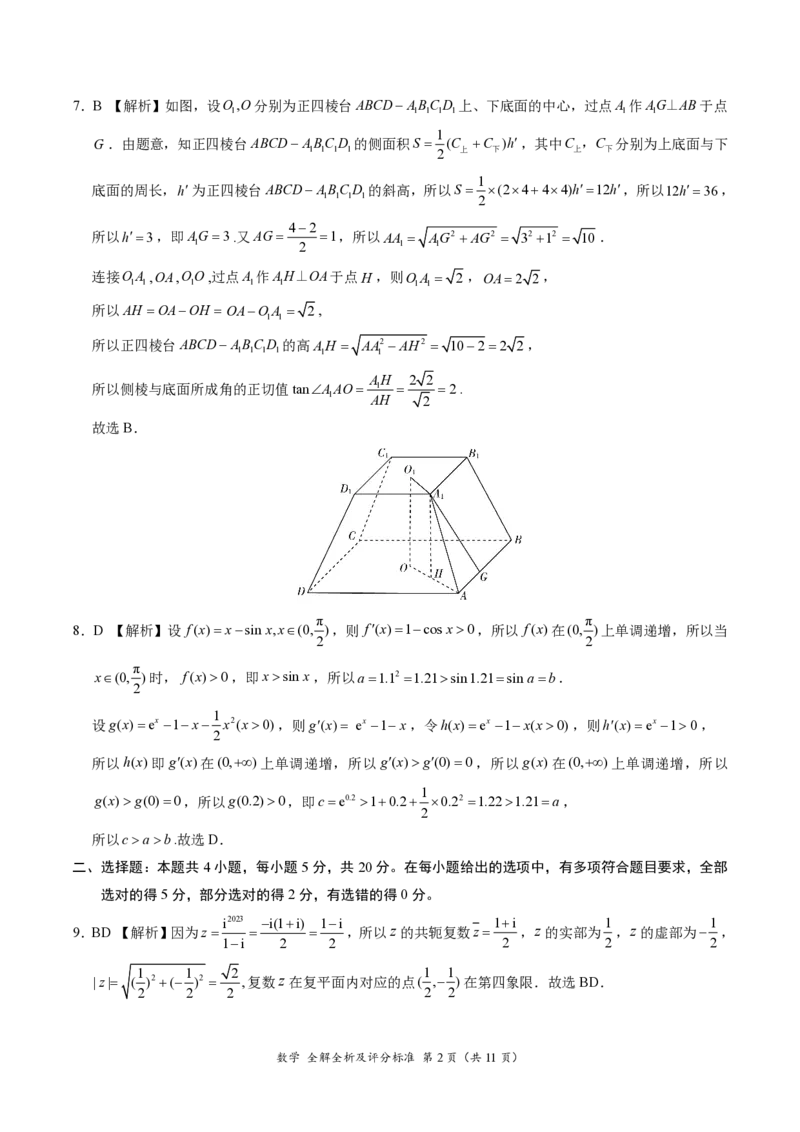QQABJYYQoggAABIAAQhCUwUCCAEQkAACCAoGwBAEMAABwRNABAA=}#}7．B 【解析】如图，设O,O分别为正四棱台ABCD ABC D 上、下底面的中心，过点A 作AG⊥AB于点 1 1 1 1 1 1 1 1 G ．由题意，知正四棱台ABCD ABC D 的侧面积S  (C C )h，其中C ，C 分别为上底面与下 1 1 1 1 2 上 下 上 下 1 底面的周长，h为正四棱台ABCD ABC D 的斜高，所以S  (2444)h12h，所以12h36， 1 1 1 1 2 42 所以h3，即AG3.又AG 1，所以AA  AG2 AG2  32 12  10 ． 1 2 1 1 连接OA ,OA,OO,过点A 作AH⊥OA于点H，则O A  2 ，OA2 2， 1 1 1 1 1 1 1 所以AH OAOH  OAOA  2, 1 1 所以正四棱台ABCD ABC D 的高AH  AA2 AH2  102 2 2， 1 1 1 1 1 1 AH 2 2 所以侧棱与底面所成角的正切值tanAAO 1  2. 1 AH 2 故选B． π π 8．D 【解析】设 f(x)xsin x,x(0, )，则 f(x)1cosx0，所以 f(x)在(0, )上单调递增，所以当 2 2 π x(0, )时， f(x)0，即xsin x，所以a1.12 1.21sin1.21sinab． 2 1 设g(x)ex 1x x2(x0)，则g'(x) ex 1x，令h(x)ex 1x(x0)，则h'(x)ex 10， 2 所以h(x)即g'(x)在(0,)上单调递增，所以g(x)g(0)0，所以g(x)在(0,)上单调递增，所以 1 g(x)g(0)0，所以g(0.2)0，即ce0.2 10.2 0.22 1.221.21a， 2 所以cab.故选D． 二、选择题：本题共4小题，每小题5分，共20分。在每小题给出的选项中，有多项符合题目要求，全部 选对的得5分，部分选对的得2分，有选错的得0分。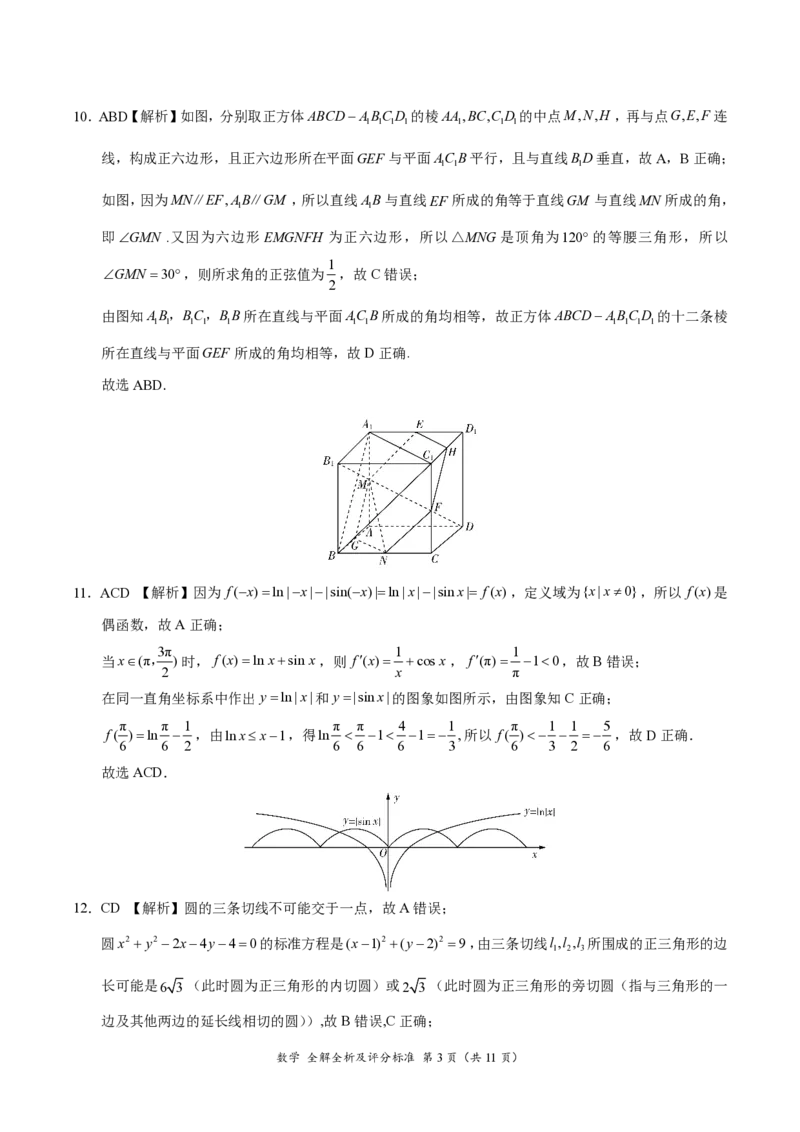 i2023 i(1i) 1i 1i 1 1 9．BD 【解析】因为z   ，所以z的共轭复数z ，z的实部为 ，z的虚部为 ， 1i 2 2 2 2 2 1 1 2 1 1 |z| ( )2 ( )2  ,复数z在复平面内对应的点( , )在第四象限．故选BD． 2 2 2 2 2 数学 全解全析及评分标准 第2页（共11页） {#{QQABJYYQoggAABIAAQhCUwUCCAEQkAACCAoGwBAEMAABwRNABAA=}#}10．ABD【解析】如图，分别取正方体ABCDABCD 的棱AA,BC,CD 的中点M,N,H ，再与点G,E,F连 1 1 1 1 1 1 1 线，构成正六边形，且正六边形所在平面GEF 与平面ACB平行，且与直线BD垂直，故A，B正确； 1 1 1 如图，因为MN∥EF,AB∥GM ，所以直线AB与直线EF 所成的角等于直线GM 与直线MN 所成的角， 1 1 即GMN .又因为六边形EMGNFH 为正六边形，所以△MNG是顶角为120 的等腰三角形，所以 1 GMN 30，则所求角的正弦值为 ，故C错误； 2 由图知AB，BC，BB所在直线与平面ACB所成的角均相等，故正方体ABCDABCD 的十二条棱 1 1 1 1 1 1 1 1 1 1 1 所在直线与平面GEF 所成的角均相等，故D正确. 故选ABD. 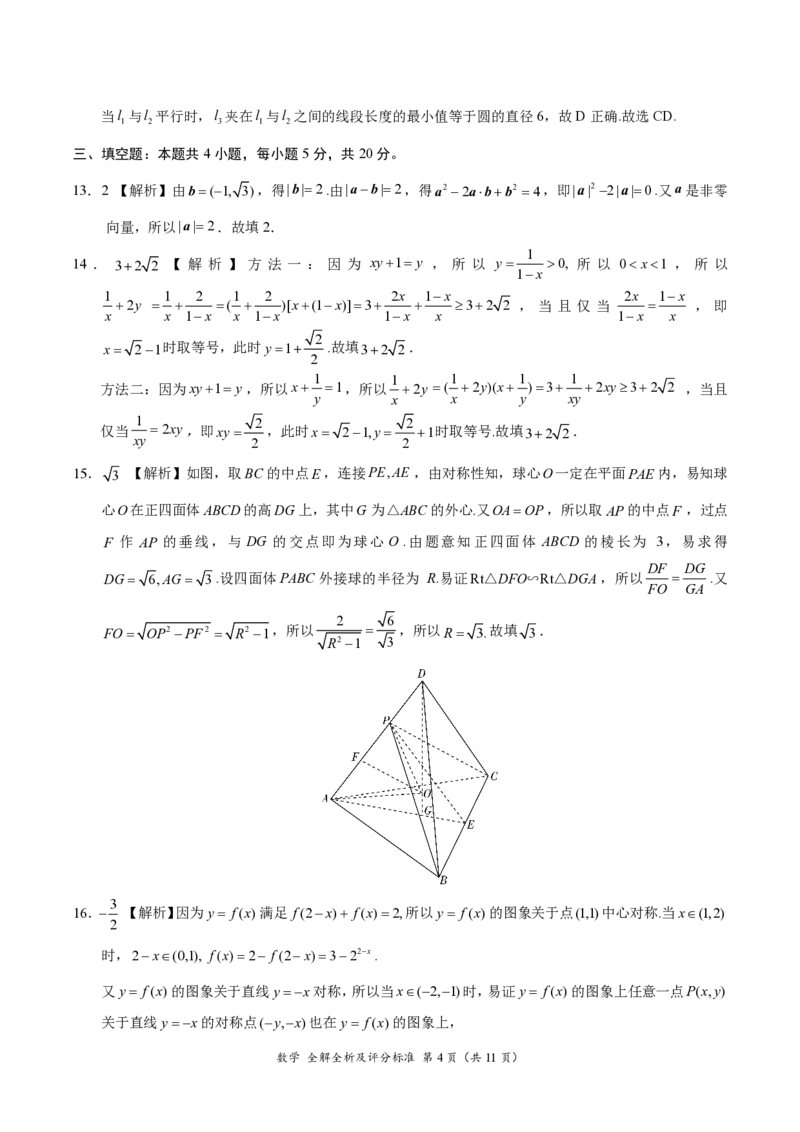11．ACD 【解析】因为 f(x)ln|x||sin(x)|ln|x||sinx| f(x)，定义域为{x|x0}，所以 f(x)是 偶函数，故A正确； 3π 1 1 当x(π， )时， f(x)ln xsin x，则 f(x) cos x， f(π) 10，故B错误； 2 x π 在同一直角坐标系中作出yln|x|和y|sinx|的图象如图所示，由图象知C正确； π π 1 π π 4 1 π 1 1 5 f( )ln  ，由lnxx1，得ln  1 1 ,所以 f( )   ，故D正确． 6 6 2 6 6 6 3 6 3 2 6 故选ACD． 12．CD 【解析】圆的三条切线不可能交于一点，故A错误； 圆x2  y2 2x4y40的标准方程是(x1)2 (y2)2 9，由三条切线l ,l ,l 所围成的正三角形的边 1 2 3 长可能是6 3（此时圆为正三角形的内切圆）或2 3（此时圆为正三角形的旁切圆（指与三角形的一 边及其他两边的延长线相切的圆））,故B错误,C正确； 数学 全解全析及评分标准 第3页（共11页） {#{QQABJYYQoggAABIAAQhCUwUCCAEQkAACCAoGwBAEMAABwRNABAA=}#}当l 与l 平行时，l 夹在l 与l 之间的线段长度的最小值等于圆的直径6，故D正确.故选CD. 1 2 3 1 2 三、填空题：本题共4小题，每小题5分，共20分。 13．2 【解析】由b(1, 3)，得|b|2.由|ab|2，得a2 2abb2 4，即|a|2 2|a|0.又a是非零 向量，所以|a|2．故填2． 1 14 ． 32 2 【 解 析 】 方 法 一 ： 因 为 xy1 y ， 所 以 y 0, 所 以 0 x1 ， 所 以 1x 1 1 2 1 2 2x 1x 2x 1x 2y   (  )[x(1x)]3  32 2 ， 当 且 仅 当  ， 即 x x 1x x 1x 1x x 1x x 2 x 21时取等号，此时y1 .故填32 2． 2 1 1 1 1 1 方法二：因为xy1 y，所以x 1，所以 2y ( 2y)(x )3 2xy32 2 ，当且 y x x y xy 1 2 2 仅当 2xy，即xy ，此时x 21,y 1时取等号.故填32 2． xy 2 2 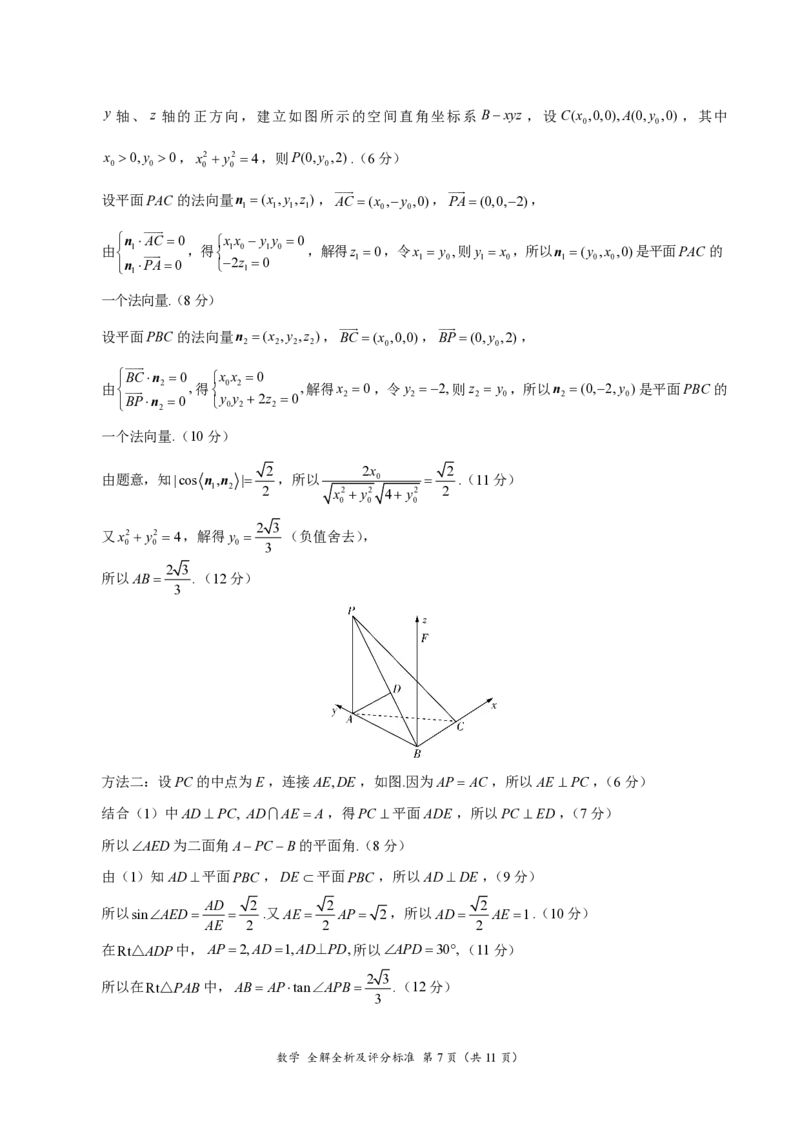15． 3 【解析】如图，取BC的中点E，连接PE,AE ，由对称性知，球心O一定在平面PAE内，易知球 心O在正四面体ABCD的高DG上，其中G 为△ABC的外心.又OAOP，所以取AP的中点F ，过点 F 作 AP 的垂线，与 DG 的交点即为球心O .由题意知正四面体 ABCD 的棱长为 3，易求得 DF DG DG 6,AG 3.设四面体PABC外接球的半径为 R.易证Rt△DFO∽Rt△DGA，所以  .又 FO GA 2 6 FO OP2 PF2  R2 1，所以  ，所以R 3.故填 3． R2 1 3 3 16． 【解析】因为y f(x)满足 f(2x) f(x)2,所以y f(x)的图象关于点(1,1)中心对称.当x(1,2) 2 时，2x(0,1), f(x)2 f(2x)322x. 又y f(x)的图象关于直线yx对称，所以当x(2,1)时，易证y f(x)的图象上任意一点P(x,y) 关于直线yx的对称点(y,x)也在y f(x)的图象上， 数学 全解全析及评分标准 第4页（共11页） {#{QQABJYYQoggAABIAAQhCUwUCCAEQkAACCAoGwBAEMAABwRNABAA=}#}所以x322y，所以ylog (x3)2, 2 3 3 所以当x(2,1)时， f(x)log (x3)2，所以 f( 23) .故填 . 2 2 2 四、解答题：本题共6小题，共70分。解答应写出文字说明、证明过程或演算步骤。 17．（10分） 【解析】（1）由a 4，a a2，知a 0， 1 n1 n n 所以lna 2lna ，（2分） n1 n lna 所以 n1 2. lna n 又lna 2ln20，（3分） 1 所以数列{lna }是等比数列．（4分） n （2） 由（1）知数列{lna }是以2ln2为首项，2为公比的等比数列， n nln2 n 所以lna 2nln2，所以b   ，（6分） n n lna 2n n 1 2 n 所以S     ①， n 2 22  2n 1 1 2 n1 n 所以 S      ②，（8分） 2 n 22 23  2n 2n1 1 1 1 1 1 n n2 ①②，得 S       1 ， 2 n 2 22 23  2n 2n1 2n1 n2 所以S 2 ．（10分） n 2n 1 1 1 1 1 n 说明：8到10分之间，若学生能用错位相减得到 S       ，可得1分. 2 n 2 22 23  2n 2n1 18．（12分） sinC sinCcosB 【解析】（1）由题意，知2sinAcosC  ，（1分） tanB sinB 所以2sinAsinBsinBcosCcosBsinC，（2分） 即2sinAsinBsin(BC)sinA.（3分） 1 由sinA0，得sinB .（4分） 2 π 5π 因为0B，所以B 或B ．（5分） 6 6 π π π π π （2）方法一：因为△ABC为锐角三角形，由（1）知B ,所以  A ， C .（6分） 6 3 2 3 2 数学 全解全析及评分标准 第5页（共11页） {#{QQABJYYQoggAABIAAQhCUwUCCAEQkAACCAoGwBAEMAABwRNABAA=}#}a2 c2 b2 3 由余弦定理的推论，得cosB  ，（7分） 2ac 2 所以a2 c2  3ac42ac，（8分） 4 所以ac ，当且仅当ac时取等号，（9分） 2 3 5 此时AC ，符合题意，（10分） 12 1 1 4 1 所以△ABC的面积S  acsinB   2 3，（11分） △ABC 2 2 2 3 2 所以△ABC面积的最大值为2 3．（12分） π π π π π 方法二：因为△ABC为锐角三角形，由（1）知B ,所以  A ， C ．（6分） 6 3 2 3 2 a b c 2 由正弦定理    4，得a4sinA,c4sinC ，（8分） sinA sinB sinC  sin 6 所以△ABC的面积 1 1 5 S  acsinB 4sinA4sinCsinB4sinAsin( A)2sinAcosA2 3sin2 A（9分） △ABC 2 2 6  sin2A 3cos2A 32sin(2A ) 32 3，（10分） 3  π 5π 当且仅当2A  ，即AC 时取等号，（11分） 3 2 12 所以△ABC面积的最大值为2 3．（12分） 说明： π 5π 第（1）问中，不写sinA0不扣分，若最后只得到B 或B 中的一个答案，扣1分. 6 6 第（2）问中若没有判断角A，C的取值范围，扣1分. 19．（12分） 【解析】（1）因为PA平面ABC，BC平面ABC，所以PABC.（1分） 因为∠ABC 90，所以BC  AB.又PA AB A，所以BC 平面PAB.（2分）  因为BC平面PBC ，所以平面PBC 平面PAB.（3分） 又ADPB, AD平面PAB，平面PAB 平面PBC PB，  所以AD平面PBC .（4分） 又PC平面PBC ，所以AD PC.（5分）    （2）方法一：过点B作BF∥AP，由题意知BC,BA,BF 两两垂直，所以以BC,BA,BF 的方向分别为x轴、 数学 全解全析及评分标准 第6页（共11页） {#{QQABJYYQoggAABIAAQhCUwUCCAEQkAACCAoGwBAEMAABwRNABAA=}#}y 轴、 z 轴的正方向，建立如图所示的空间直角坐标系 Bxyz ，设C(x ,0,0),A(0,y ,0) ，其中 0 0 x 0,y 0，x2  y2 4，则P(0,y ,2).（6分） 0 0 0 0 0   设平面PAC 的法向量n (x,y ,z )，AC (x ,y ,0)，PA(0,0,2)， 1 1 1 1 0 0   n AC 0 xx y y 0 由 n 1 1   P  A  0 ，得  1 2z 0 1 0 1 0 ，解得z 1 0，令x 1  y 0 ,则y 1  x 0 ，所以n 1 (y 0 ,x 0 ,0)是平面PAC 的 一个法向量.（8分）   设平面PBC 的法向量n (x ,y ,z )，BC (x ,0,0)，BP(0,y ,2)， 2 2 2 2 0 0   BCn 0 x x 0 由   B  P  n 2 2 0 ,得 y 0 0 y 2 2 2z 2 0 ,解得x 2 0，令y 2 2,则z 2  y 0 ，所以n 2 (0,2,y 0 )是平面PBC 的 一个法向量.（10分） 2 2x 2 由题意，知|cos n,n | ，所以 0  .（11分） 1 2 2 x2  y2 4 y2 2 0 0 0 2 3 又x2  y2 4，解得y  （负值舍去）， 0 0 0 3 2 3 所以AB .（12分） 3 方法二：设PC的中点为E，连接AE,DE，如图.因为AP AC，所以AE PC，（6分） 结合（1）中ADPC, AD AE A，得PC 平面ADE ，所以PC ED，（7分）  所以AED为二面角APCB的平面角.（8分） 由（1）知AD平面PBC ，DE平面PBC ，所以ADDE ，（9分） AD 2 2 2 所以sinAED  .又AE AP 2，所以AD AE 1.（10分） AE 2 2 2 在Rt△ADP中，AP2,AD1,AD⊥PD,所以APD30,（11分） 2 3 所以在Rt△PAB中，AB APtan∠APB .（12分） 3 数学 全解全析及评分标准 第7页（共11页） {#{QQABJYYQoggAABIAAQhCUwUCCAEQkAACCAoGwBAEMAABwRNABAA=}#}说明： 第一问： 1.指出“PABC”得1分，没有写“BC平面ABC”不扣分； 2.得到“BC 平面PAB”得1分，没有写“PA  AB A”不扣分； 3.得出“平面PBC 平面PAB”得1分，没有写“BC平面PBC ”不扣分； 4.得出“AD平面PBC ”得1分，没有写“AD平面PAB，平面PAB  平面PBC PB”不扣分； 5.得出“ADPC”得1分，没有写“PC平面PBC ”不扣分； 或者另解：因为AD平面PBA，所以BC  AD.（3分） 又ADPB, PB  BC B，所以AD平面PBC .（4分） 又PC平面PBC ，所以AD PC.（5分） 第二问： 方法一：1.建系设点得1分； 2.得到“平面PAC 的一个法向量是(y ,x ,0)”得2分； 0 0 3.得出“平面PBC 的一个法向量是(0,2,y )”得2分； 0 2x 2 4.代入得出“ 0  ”得1分； x2  y2 4 y2 2 0 0 0 2 3 5.得出“AB ”得1分. 3 方法二：1.指出“AE PC”得1分； 2.得到“PC ED”得1分； 3.指出“AED为二面角APCB的平面角”得1分； 4.得出“ADDE ”得1分； 5.得出“AD1”得1分； 6.得出“APD30”得1分； 2 3 7.得出“AB ”得1分. 3 数学 全解全析及评分标准 第8页（共11页） {#{QQABJYYQoggAABIAAQhCUwUCCAEQkAACCAoGwBAEMAABwRNABAA=}#}20．（12分） 【解析】（1）设圆C的标准方程为(xa)2 (yb)2 r2(a0,b0,r0). 由题意，知圆心O(0,0). 因为直线OC与直线l:x y40平行，所以直线OC:y x，所以ba.（1分） 因为圆O：x2  y2 2与圆C外切， 所以 a2b2 r 2，即 2ar 2 .（2分） 因为圆C与直线l:x y40相切， |aa4| 所以 r，解得r2 2，（3分） 2 把r2 2代入 2ar 2 ，得a3，（4分） 所以圆C的标准方程为(x3)2 (y3)2 8.（5分） （2）设点C关于直线l的对称点为C(m,n)， n3 1 m3 n3  m3 由CCl及CC的中点( , )在直线l上，得 ，（6分） 2 2 m3 n3   40  2 2 m7 解得 ，所以C(7,1).（7分） n1 由对称性得|PC||PC|， 所以|AP||PC||AP||PC||AC|，当且仅当A,P,C三点共线时取等号，（8分） 11 1 所以直线AC的斜率为  ，（9分） 7(1) 4 1 所以直线AC的方程为y1 (x1)，即x4y30，（10分） 4 3 3 17 所以圆心O到直线AC的距离d   ，（11分） 1242 17 10 17 所以|AB|2 2d2  .（12分） 17 说明：根据评分标准酌情给分. 21．（12分） 【解析】（1）由2(an11)c 2(an 1)c c c 两边同时除以c c ， n n1 n1 n n1 n 得2b 2b 1，（2分） n1 n 1 1 1 n 所以b b  ,所以数列{b }为等差数列，公差为 ，又b  ，所以b  ，（4分） n1 n 2 n 2 1 2 n 2 数学 全解全析及评分标准 第9页（共11页） {#{QQABJYYQoggAABIAAQhCUwUCCAEQkAACCAoGwBAEMAABwRNABAA=}#}1 4 1 1 所以  4(  )，（5分） bb n(n1) n n1 n n1 1 1 1 1 1 1 所以T 4(1      )4(1 )4．（6分） n 2 2 3  n n1 n1 n 2(an 1) （2）因为b  ，所以c  ，（7分） n 2 n n 2(an11) 2(an 1) 2nan12(n1)an 2 所以c c    ，（8分） n1 n n1 n n(n1) 令 f(a)nan1(n1)an 1(a0，且a1)，（9分） 则 f(a)n(n1)an (n1)nan1 n(n1)an1(a1)， 当a(0,1)时， f(a)0，当a(1,)时， f(a)0， 所以 f(a)在(0,1)上单调递减，在(1,)上单调递增，所以 f(a) f(1)0．（11分） 所以c c 0，即c c ，所以数列{c }为递增数列．（12分） n1 n n1 n n 说明： 第（1）问中，由2(an11)c 2(an 1)c c c 两边同时除以c c ，但没有整理出2b 2b 1， n n1 n1 n n1 n n1 n 1 也可得1分；若T 表达式写正确，但没有整理出T 4(1 )不扣分，但T 表达式整理错误要扣1分. n n n1 n 第（2）问若写出了c c 的表达式，但化简错误不得分，化简正确但未通过正确步骤分析出c c 0 n1 n n1 n 而直接得出结论，扣3分. 22．（12分） x2 【解析】（1）对 f(x)求导，得 f(x)lnx ，所以 f(1)1．（1分） x 又 f(1)0，所以曲线y f(x)在点(1, f(1))处的切线方程为yx1，所以g(x)x1．（2分） 2 令h(x) f(x)g(x)(x2)lnxx1,x0，则h(x)lnx2 ,令h(x)0,得x1，（3分） 1 1 x 1 所以当0 x1时,h(x)0, h (x)单调递减, 1 1 当x1时,h(x)0, h (x)单调递增,所以h(x)h(1)0,（4分） 1 1 1 1 所以对任意正实数x，都有 f(x)g(x)．（5分） （2）易知曲线y f(x)在点(2, f(2))处的切线方程为y(x2)ln2.(6分) 令s(x)(x2)ln2，下证当x0时， f(x)s(x)，令h (x) f(x)s(x)(x2)(lnxln2),x0， 2 当0 x2时，x20,lnxln20,所以h (x)0，即 f(x)s(x)． 2 当x2时，x20,lnxln20,所以h (x)0,即 f(x)s(x)． 2 数学 全解全析及评分标准 第10页（共11页） {#{QQABJYYQoggAABIAAQhCUwUCCAEQkAACCAoGwBAEMAABwRNABAA=}#}综上，当x0时， f(x)s(x).（7分） x2 2 易知 f(x)lnx lnx 1在(0,)上单调递增， x x 且 f(1)10, f(2)ln20, 2 由函数零点存在定理，得 f(x)在(1,2)上存在唯一零点x ,即lnx  1，x (1,2).（8分） 0 0 x 0 0 当x(0,x )时， f(x)0，当x(x ,)时， f(x)0, 0 0 所以 f(x)在(0,x )上单调递减，在(x ,)上单调递增， f(x)  f(x )(x 2)lnx .（9分） 0 0 min 0 0 0 2 2 4 又lnx  1，所以 f(x) (x 2)( 1)4(x  )0, 0 x min 0 x 0 x 0 0 0 当0 x1时， f(x)(x2)lnx0，当1 x x 时， f(x)(x2)lnx0， 0 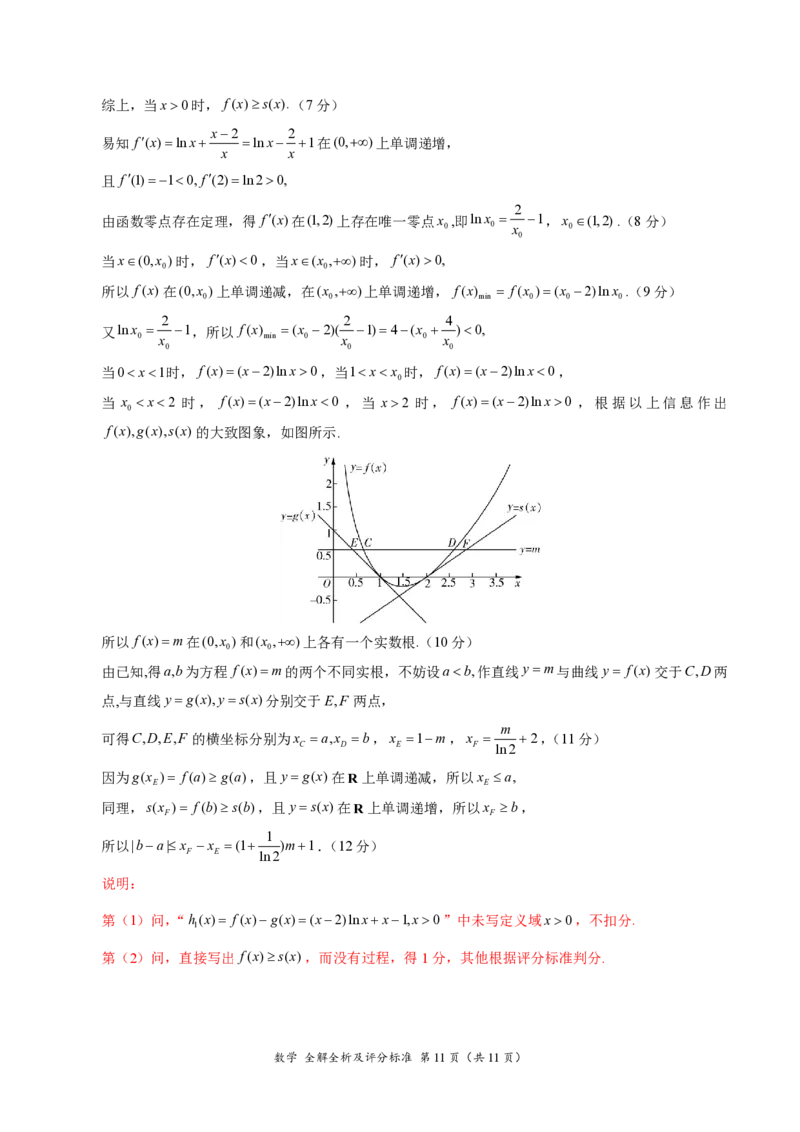当 x  x2 时， f(x)(x2)lnx0 ，当 x2 时， f(x)(x2)lnx0 ，根据以上信息作出 0 f(x),g(x),s(x)的大致图象，如图所示. 所以 f(x)m在(0,x )和(x ,)上各有一个实数根.（10分） 0 0 由已知,得a,b为方程 f(x)m的两个不同实根，不妨设ab,作直线ym与曲线y f(x)交于C,D两 点,与直线yg(x),ys(x)分别交于E,F 两点， m 可得C,D,E,F 的横坐标分别为x a,x b，x 1m，x  2，（11分） C D E F ln2 因为g(x ) f(a) g(a)，且yg(x)在R上单调递减，所以x a, E E 同理，s(x ) f(b)s(b)，且ys(x)在R上单调递增，所以x b， F F 1 所以|ba|x x (1 )m1．（12分） F E ln2 说明： 第（1）问，“h(x) f(x)g(x)(x2)lnxx1,x0”中未写定义域x0，不扣分. 1 第（2）问，直接写出 f(x)s(x)，而没有过程，得1分，其他根据评分标准判分. 数学 全解全析及评分标准 第11页（共11页） {#{QQABJYYQoggAABIAAQhCUwUCCAEQkAACCAoGwBAEMAABwRNABAA=}#}