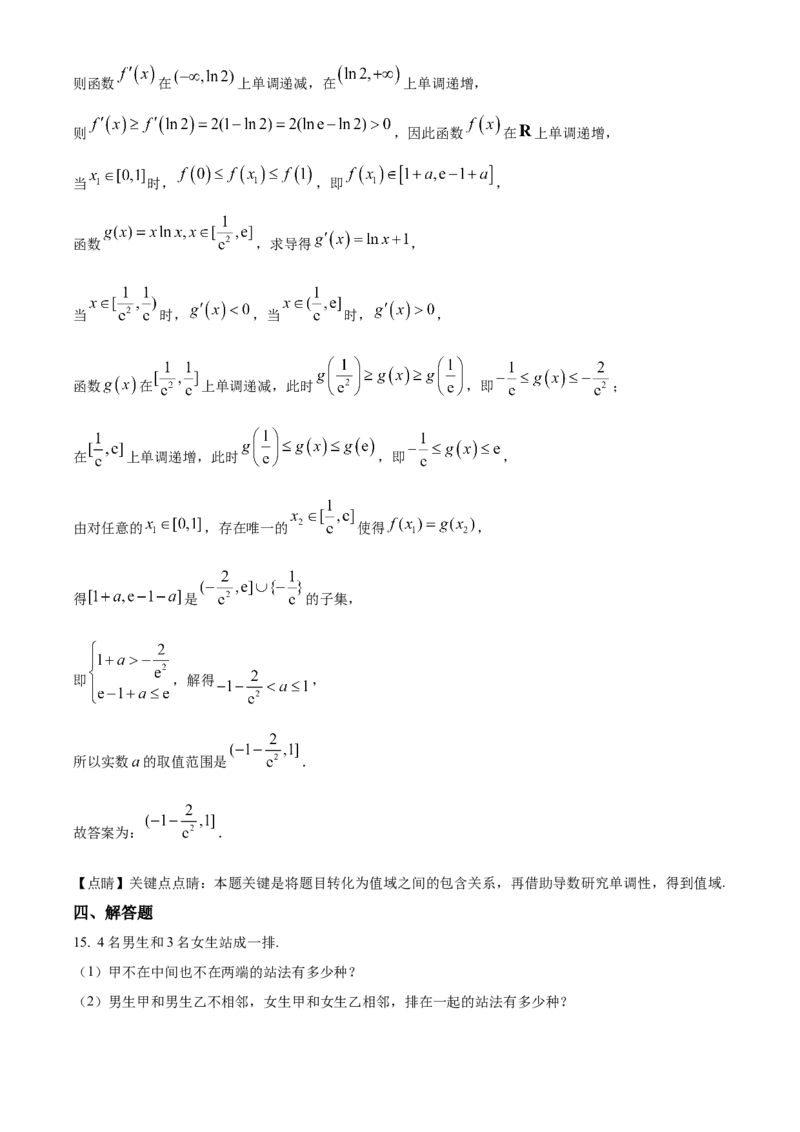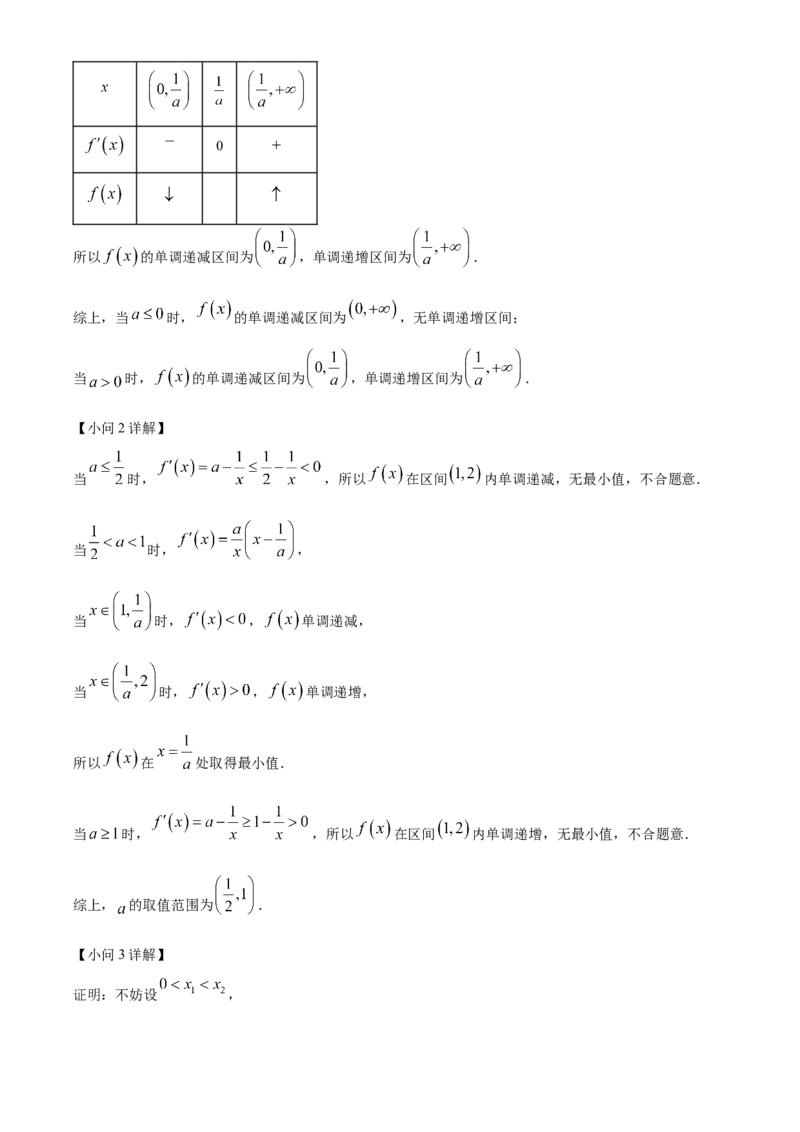文档内容
八一路校区高二数学第一次月考测试
一、单选题
1. 若函数 在 处可导,且 ,则 ( )
A. B. C. 1 D. 2
【答案】C
【解析】
【分析】由导数的概念可解.
【详解】 .
故选:C
2. 甲、乙、丙、丁、戊、己六人站成一排合影留念,则甲、乙两人中间恰好有两人的站法有( )
A. 36种 B. 72种 C. 144种 D. 288种
【答案】C
【解析】
【分析】由排列数的计算公式,结合分步乘法计数原理代入计算,即可得到结果.
【详解】第一步从6个位置中选择2个位置,满足条件的选位可以是 ,
共有3种不同 的方法;
第二步将甲、乙排到所选择的2个位置,共有 种不同的方法;
第三步将丙、丁、戊、己排到剩余的4个位置,共有 种不同的方法;
由分步计数原理可知,共有 种.
故选:C
3. 拉格朗日中值定理是微分学中的基本定理之一,定理内容是:如果函数 在闭区间 上的图象
连续不间断,在开区间 内的导数为 ,那么在区间 内至少存在一点c,使得
成立,其中c叫做 在 上的“拉格朗日中值点”.根据这个定理,可得函数 在 上的“拉格朗日中值点”的个数为( ).
A. 3 B. 2 C. 1 D. 0
【答案】B
【解析】
【分析】根据题中给出的“拉格朗日中值点”的定义分析求解即可.
【详解】函数 ,求导得: ,令 为 在 上的“拉格朗日中值点”,
则有 ,即 ,
整理得 ,解得 ,
所以函数 在 上的“拉格朗日中值点”的个数为2.
故选:B.
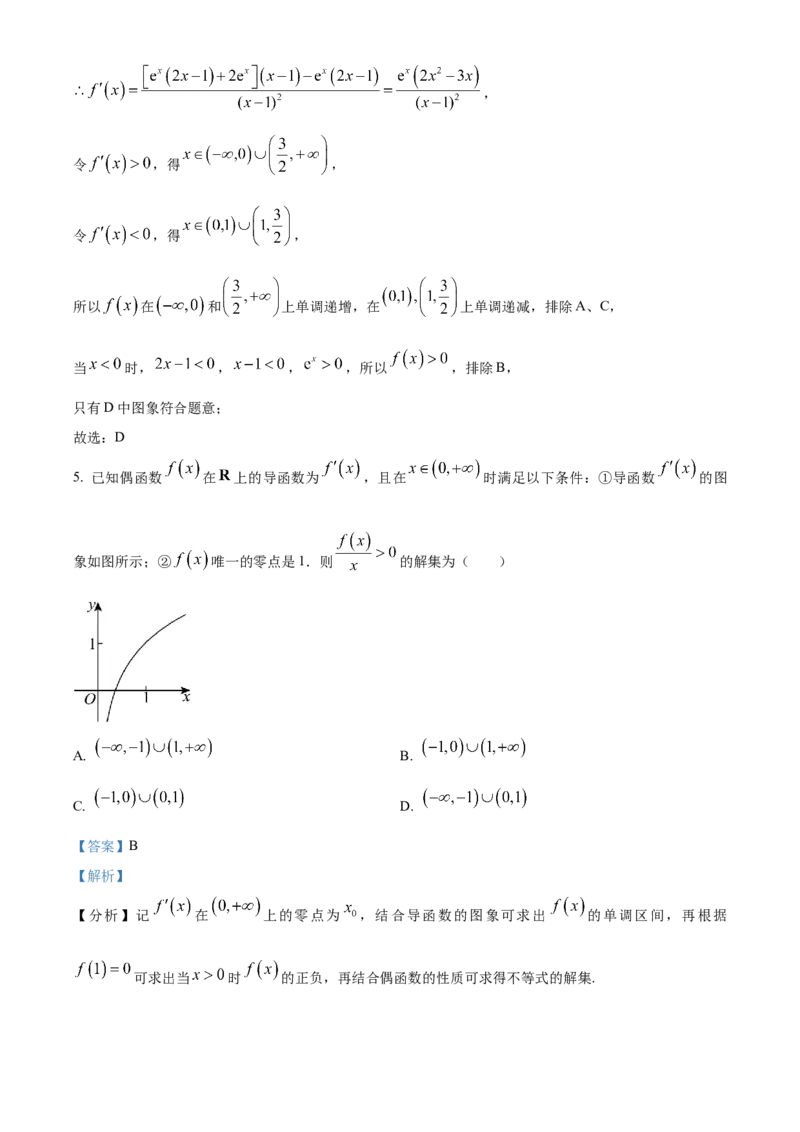
4. 函数 的大致图象是( )
A. B.
C. D.
【答案】D
【解析】
【分析】求出函数的导数,利用导数判定函数的单调性即可得出选项.
【详解】解: ,定义域为 ,,
令 ,得 ,
令 ,得 ,
所以 在 和 上单调递增,在 上单调递减,排除A、C,
当 时, , , ,所以 ,排除B,
只有D中图象符合题意;
故选:D
5. 已知偶函数 在 上的导函数为 ,且在 时满足以下条件:①导函数 的图
象如图所示;② 唯一的零点是1.则 的解集为( )
A. B.
C. D.
【答案】B
【解析】
【分析】记 在 上的零点为 ,结合导函数的图象可求出 的单调区间,再根据
可求出当 时 的正负,再结合偶函数的性质可求得不等式的解集.【详解】记 在 上的零点为 ,
由 在 上的图象,知当 时, ,当 时, ,
所以 在 上单调递减,在 上单调递增.
因为 在 唯一的零点是1,即 ,
所以当 时, ,当 时, .
又 为偶函数,所以当 时, ,当 时, ,
所以 的解集为 .
故选:B.
6. 已知函数 ,则 (
)
A. 2024 B. C. 2025 D. 2026
【答案】B
【解析】
【分析】通过求导得到 的对称中心,然后利用对称性求函数值即可.
【详解】由 ,可得 .
令 ,得 ,
又 ,所以 图象的对称中心为 ,
, , ,.
故选:B.
7. 在 上的导函数为 ,则下列不等式成立的是( )
A. B.
C. D.
【答案】A
【解析】
【分析】根据条件构造函数 ,利用导数判断其单调性,从而得到不等关系,即可判
断.
【详解】令 ,
则 ,
, ,
在 上单调递增,
,即 ,
.
故选:A.
8. 已知 对 恒成立,则实数 的取值范围是( )
A. B. C. D.
【答案】A【解析】
【分析】将不等式 进行变形,构造函数 ,根据其单调性得到 ,转化为
恒成立问题,通过求函数 在 上的最大值来确定 的取值范围.
【详解】设 ,则 .
∵ 时, , ,∴ ,故 在 上单调递增.
∵ 对 恒成立,∴当 时, ,则有 ,
当 时, 可等价变形为 .
∵ 在 上单调递增,且 , ( ),
∴由 可得 ,即 对 恒成立.
设 ,则 .
当 时, , , ,故 .
∴ 在 上单调递减,
∴当 时, .
∵ 对 恒成立,
∴ ,即实数 的取值范围是 .
故选:A.【点睛】关键点点睛:解决本题的关键是把不等式 等价变形为 ,通过
构造函数,最终问题转化为转化为 恒成立问题.
二、多选题
9. 定义在 上的函数 的导函数 的图象如图所示,则下列结论正确的是( )
A. 函数 在 上单调递减 B. 函数 在 上单调递减
C. 函数 在 处取得极小值 D. 函数 在 处取得极大值
【答案】AD
【解析】
【分析】利用函数的函数的图象,可判断函数的单增区间与单减区间,进而可得极大值点,从而可得结论.
【详解】由函数 的导函数 的图象可知,
当 时, ,所以 在 上单调递增,故B错误;
当 时, ,所以 在 上单调递减,故A正确;
所以函数 在 处取得极大值, 不是极小值点,故C错误,D正确.
故选:AD.
10. 设函数 ,则( )
A. 函数 有两个极值点
B. 函数 有两个零点
C. 直线 是曲线 的切线D. 点 是曲线 的对称中心
【答案】ABD
【解析】
【分析】求导,确定函数单调性极值,即可判断AB,由导数的几何意义可判断C,由对称中心的概念可
判断D;
【详解】
令 解得 ,令 解得 或 ,
所以 在 单调递增, 单调递减, 单调递增,
因为 ,极大值 ,且极小值 ,
所以函数有两个极值点,有两个零点,故AB正确,
令 即 , ,无解;
故C错误;
,
所以 ,即点 是曲线 的对称中心,正确;
故选:ABD
.
11 设函数 ,则( )
A. 当 时, 是 的极大值点
B. 当 时, 有三个零点
C. 存在a,使得点 为曲线 的对称中心D. 存在a,b,使得 为曲线 的对称轴
【答案】BC
【解析】
【分析】A选项,根据极值和导函数符号的关系进行分析;B选项,先分析出函数的极值点为 ,
根据零点存在定理和极值的符号判断出 在 上各有一个零点;C选项,若存在这
样的 ,使得 为 的对称中心,则 ,据此进行计算判断,亦可利用
拐点结论直接求解.
D选项,假设存在这样的 ,使得 为 的对称轴,则 为恒等式,据此计算
判断;
【详解】A选项, , 时, , 单调递减,
时 , 单调递增,
此时 在 处取到极小值,A选项错误;
B选项, ,由于 ,
故 时 ,故 在 上单调递增,
时, , 单调递减,
则 在 处取到极大值,在 处取到极小值,
由 , ,则 ,
根据零点存在定理 在 上有一个零点,
又 , ,则 ,
则 在 上各有一个零点,于是 时, 有三个零点,B选项正确;
C选项,方法一:利用对称中心的表达式化简
,若存在这样的 ,使得 为 的对称中心,
则 ,事实上,
,
于是
即 ,解得 ,即存在 使得 是 的对称中心,C选项正确.
方法二:直接利用拐点结论
任何三次函数都有对称中心,对称中心的横坐标是二阶导数的零点,
, , ,
由 ,于是该三次函数的对称中心为 ,
由题意 也是对称中心,故 ,
即存在 使得 是 的对称中心,C选项正确.
D选项,假设存在这样的 ,使得 为 的对称轴,
即存在这样的 使得 ,
即 ,
根据二项式定理,等式右边 展开式含有 的项为 ,
于是等式左右两边 的系数都不相等,原等式不可能恒成立,
于是不存在这样的 ,使得 为 的对称轴,D选项错误;
故选:BC【点睛】结论点睛:(1) 的对称轴为 ;(2) 关于 对称
;(3)任何三次函数 都有对称中心,对称中心是三
次函数的拐点,对称中心的横坐标是 的解,即 是三次函数的对称中心.
三、填空题
12. 函数 在 处有极值10,则实数 _________.
【答案】
【解析】
【分析】将函数求导,由题意得 和 ,联立求得 ,再回代检验是否符合题意即得.
【详解】由 求导得, ,
依题意, ①, ②,
联立① ,② ,解得: 或 .
当 , 时, ,
,函数 为增函数,显然不符合题意,故舍去;
当 , 时, ,
,当 时, ,此时 为减函数,
当 时, ,此时 为增函数,故 在 处有极小值为 ,符合题意.
故答案为: .
13. 若函数 在区间 上有单调递增区间,则实数 的取值范围是______.【答案】
【解析】
【分析】根据题意转化为 在 上有解,分离参数后求函数最值即可得解.
【详解】 ,由题意 在 上有解,
即 在 上有解,
根据对勾函数的性质可知, 在 上单调递增,所以在 时取最大值,
故 ,故实数 的取值范围是 .
故答案为:
14. 对于函数 ,若对任意的 ,存在唯一的 使得
,则实数 的取值范围是__________.
【答案】
【解析】
【分析】借助导数研究单调性,并求出函数在给定区间上的值域,再结合集合包含关系,列出不等式解题
即可.
【详解】函数 ,求导 ,
令 ,求导 ,
函数 在 上单调递增,当 时, ;当 时, ,则函数 在 上单调递减,在 上单调递增,
则 ,因此函数 在 上单调递增,
当 时, ,即 ,
函数 ,求导得 ,
当 时, ,当 时, ,
函数 在 上单调递减,此时 ,即 ;
在 上单调递增,此时 ,即 ,
由对任意的 ,存在唯一的 使得 ,
得 是 的子集,
即 ,解得 ,
所以实数 的取值范围是 .
故答案为: .
【点睛】关键点点睛:本题关键是将题目转化为值域之间的包含关系,再借助导数研究单调性,得到值域.
四、解答题
15. 4名男生和3名女生站成一排.
(1)甲不在中间也不在两端的站法有多少种?
(2)男生甲和男生乙不相邻,女生甲和女生乙相邻,排在一起的站法有多少种?(3)甲、乙、丙三人从左到右顺序一定的站法有多少种?
【答案】(1)2880
(2)960 (3)840
【解析】
【分析】(1)根据题意先排甲,然后剩余的进行全排列即可;
(2)利用捆绑法,将女生甲和女生乙捆绑在一起,与除去男生甲和男生乙的其他人进行全排列,然后男
生甲和乙插空即可;
(3)7个全排列后,除以甲、乙、丙的全排列数即可.
【小问1详解】
分两步,先排甲有 种,其余有 种,
所以根据分步乘法原理知共有 种排法.
【小问2详解】
分三步:
① 捆绑法,现将女生甲与女生乙捆绑在一起,有 (种);
②将女生甲和女生乙看成整体,与其他人(除去男生甲和男生乙)排列,有 (种);
③插空法,在其他人排好的基础上,将男生甲和乙插空(共有5个空位置),有 (种),
所以根据分步乘法原理可知共有 (种).
【小问3详解】
7人共有 种排法,其中甲、乙、丙三人有 种排法,
因而在 种排法中每 种对应一种符合条件的排法,
故共有 种排法
16. 已知函数 .
(1)若 ,求曲线 在点 处的切线方程;
(2)证明:当 时, .【答案】(1)
(2)证明见解析
【解析】
【分析】(1)将 代入函数解析式,对函数求导,求 确定斜率,求 确定切点坐标,
利用点斜式即可求切线方程.
(2)根据 ,确定函数 ,令 ,利用二次求导的方法
确定 的单调性,再根据 ,确定函数 的单调区间,从而求出函数 的最小值,即
,由此结论得证.
【小问1详解】
当 时, ,则 ,
得 ,又 ,所以切点为 ,所以切线方程为 ,
即 .
【小问2详解】
因为 ,所以 ,所以 ,
令 ,所以 ,
令 ,所以 ,
因为 , 时, ,所以 ,
所以 在 上单调递增,又 ,
所以当 时, ,当 时, ,所以 在 上单调递减,在 上单调递增,
所以 ,所以 ,所以 ,
即 .
17. 已知函数 ,其中 .
(1)若 的图象在 处的切线经过点 ,求a的值;
(2)讨论 的单调性.
【答案】(1)
(2)答案见解析
【解析】
【分析】(1)求导求出切线的斜率和切点坐标,由直线的点斜式方程求出切线方程,再代入经过点的坐
标可得答案;
(2)求导,分 、 、 、 讨论,可得答案.
【小问1详解】
,
因为 , ,
所以 的图象在 处的切线方程为 ,
将 代入得 ,解得 ;
【小问2详解】
,当 时, ,令 ,得 ;令 ,得 ,
所以 在 上单调递增,在 上单调递减.
当 时, ,所以 在 上单调递增.
当 时,令 ,得 或 ;令 ,得 ,
所以 在 , 上单调递增,在 上单调递减.
当 时,令 ,得 或 ;令 ,得 ,
所以 在 , 上单调递增,在 上单调递减.
综上,当 时, 在 上单调递增,在 上单调递减;
当 时, 在 , 上单调递增,在 上单调递减;
当 时, 在 上单调递增;
当 时, 在 , 上单调递增,在 上单调递减.
18. 已知函数 .
(1)求函数 的单调区间;
(2)求证:函数 的图象在x轴上方.
【答案】(1)单调递增区间为 ,单调递减区间为 ;
(2)证明见解析.
【解析】
【分析】(1)求 ,根据 正负即可求y的单调区间;
(2)求 ,根据 零点的范围求出g(x)的最小值,证明其最小值大于零即可.
【小问1详解】,
令 则 .
当 时, ,∴函数在 上单调递增;
在
当 时, ,∴函数 上单调递减.
的
即 单调递增区间是 ,单调递减区间是 ;
【小问2详解】
,
,易知 单调递增,
又 , ,
∴在 上存在一个 ,
使得: ,即: ,且 ,
当 ,有 单调递减;
当 ,有 单调递增.
∴ ,
∴ ,
∴函数 的图象在x轴上方.
【点睛】本题考查隐零点,关键是判断 单调,且 , ,由此得出在(1,2)之间存在零点 ,据此求出g(x)的最小值,证明此最小值大于零即可.
19. 已知函数 .
(1)求 的单调区间;
(2)若 在区间 内有最小值,求 的取值范围;
(3)若关于 的方程 有两个不同的解 , ,求证: .
【答案】(1)答案见解析
(2)
(3)证明见解析
【解析】
【分析】(1)求出 的导数,通过讨论 的范围,判断 的符号,得到函数 的单调区间即
可;
(2)通过讨论 的范围,判断 在区间 内单调性,从而得出 的取值范围;
(3)根据题意分析可得:若 , 是关于 的方程 的两个不同的解,通过联立方程组消去 ,
再通过换元 ,整理得到 ,结合的 单调性分析运算得到
,从而 得证.
【小问1详解】
的定义域为 , ,
当 时, ,所以 的单调递减区间为 ,无单调递增区间;
当 时, , 随 的变化情况如下表所示:0
所以 的单调递减区间为 ,单调递增区间为 .
综上,当 时, 的单调递减区间为 ,无单调递增区间;
当 时, 的单调递减区间为 ,单调递增区间为 .
【小问2详解】
当 时, ,所以 在区间 内单调递减,无最小值,不合题意.
当 时, ,
当 时, , 单调递减,
当 时, , 单调递增,
所以 在 处取得最小值.
当 时, ,所以 在区间 内单调递增,无最小值,不合题意.
综上, 的取值范围为 .
【小问3详解】
证明:不妨设 ,由题意得 消去 得 ,
设 ,代入上式得 ,
,
下证 ,
即证 .
设 ,则 ,
令 ,则 ,
所以 在区间 内单调递增,即 ,
所以 在区间 内单调递增,即 ,
所以 ,所以 ,
因为 , ,所以 .