文档内容
梅河口市第五中学 2023~2024 学年度下学期
高二数学 6 月月考试题
说明:本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷1至2页,第Ⅱ卷3至4页,共4
页。满分150分,考试时间120分钟。
第 Ⅰ 卷
(选择题,共58分)
注意事项:
1.答卷前,考生务必将自己的姓名、考号填写在答题卡上并将条形码粘贴在粘贴处。
2.回答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动,
用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写在本试卷上无
效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项
是符合题目要求的.
1.若随机变量 ,且 ,则 ( )
A.0.29 B.0.71 C.0.79 D.0.855
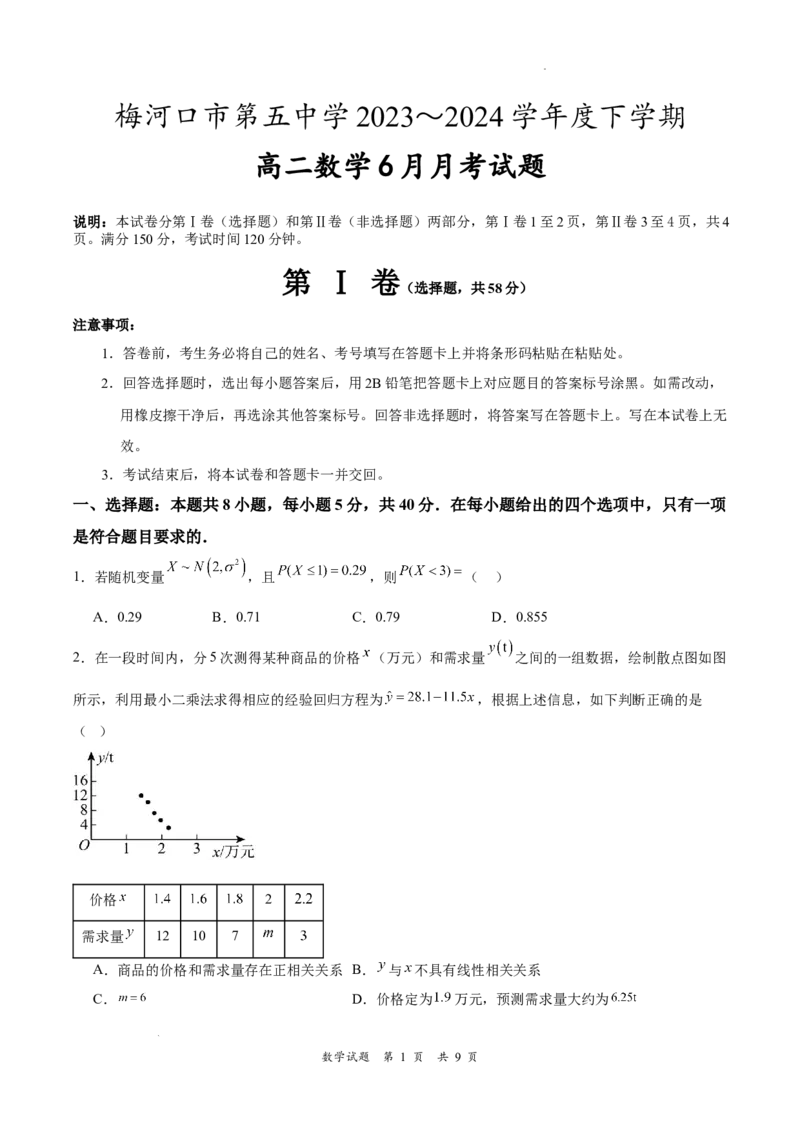
2.在一段时间内,分5次测得某种商品的价格 (万元)和需求量 之间的一组数据,绘制散点图如图
所示,利用最小二乘法求得相应的经验回归方程为 ,根据上述信息,如下判断正确的是
( )
价格 2
需求量 12 10 7
A.商品的价格和需求量存在正相关关系 B. 与 不具有线性相关关系
C. D.价格定为 万元,预测需求量大约为
数学试题 第 1 页 共 9 页
学科网(北京)股份有限公司3. 展开式中 的系数为( )
A. B.5 C.15 D.35
4.一玩具制造厂的某一配件由A、B、C三家配件制造厂提供,根据三家配件制造厂以往的制造记录分析
得到数据:制造厂A、B、C的次品率分别为 ,提供配件的份额分别为 ,设三
家制造厂的配件在玩具制造厂仓库均匀混合且不区别标记,从中随机抽取一件配件,则抽到的是次品的概
率为( )
A.0.0135 B.0.0115 C.0.0125 D.0.0145
5.质数(prime number)又称素数,一个大于1的自然数,除了1和它本身外,不能被其他自然数整除,
则这个数为质数.数学上把相差为2的两个素数叫做“孪生素数”如:3和5,5和 ,那么,如果我们
在不超过40的自然数中,随机选取两个不同的数,记事件A:这两个数都是素数.事件B:这两个数不是
孪生素数,则 ( )
A. B. C. D.
6.著名数学家欧几里得著的《几何原本》中记载:任何一个大于1的整数要么是一个素数,要么可以写成
一系列素数的积,例如 .对于 ,其中 均是素数,则从
中任选3个数,可以组成不同三位数的个数为( )
A.18 B.32 C.36 D.42
7.现将包含甲、乙在内的5名老师全都安排到3个不同的班级,每个班级必须至少有1名老师,且甲、乙
必须去同一个班级,则不同的选派方案共有( )
A.144种 B.72种 C.36种 D.18种
8.三个男生三个女生站成一排,已知其中女生甲不在两端,则有且只有两个女生相邻的概率是( )
A. B. C. D.
数学试题 第 2 页 共 9 页
学科网(北京)股份有限公司二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题
目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.下列说法正确的是( )
A.将一组数据的每一个数减去同一个数后,新数据的方差与原数据方差相同
B.线性回归直线^y=b^x+a^一定过样本点中心
C.线性相关系数 越大,两个变量的线性相关性越强
D.在残差的散点图中,残差分布的水平带状区域的宽度越窄,其模型的拟合效果越好
10.已知 的二项展开式中二项式系数之和为64,下列结论正确的是( )
A.二项展开式中各项系数之和为
B.二项展开式中二项式系数最大的项为第四项
C.二项展开式中有3个有理项
D.二项展开式中系数最大的项为
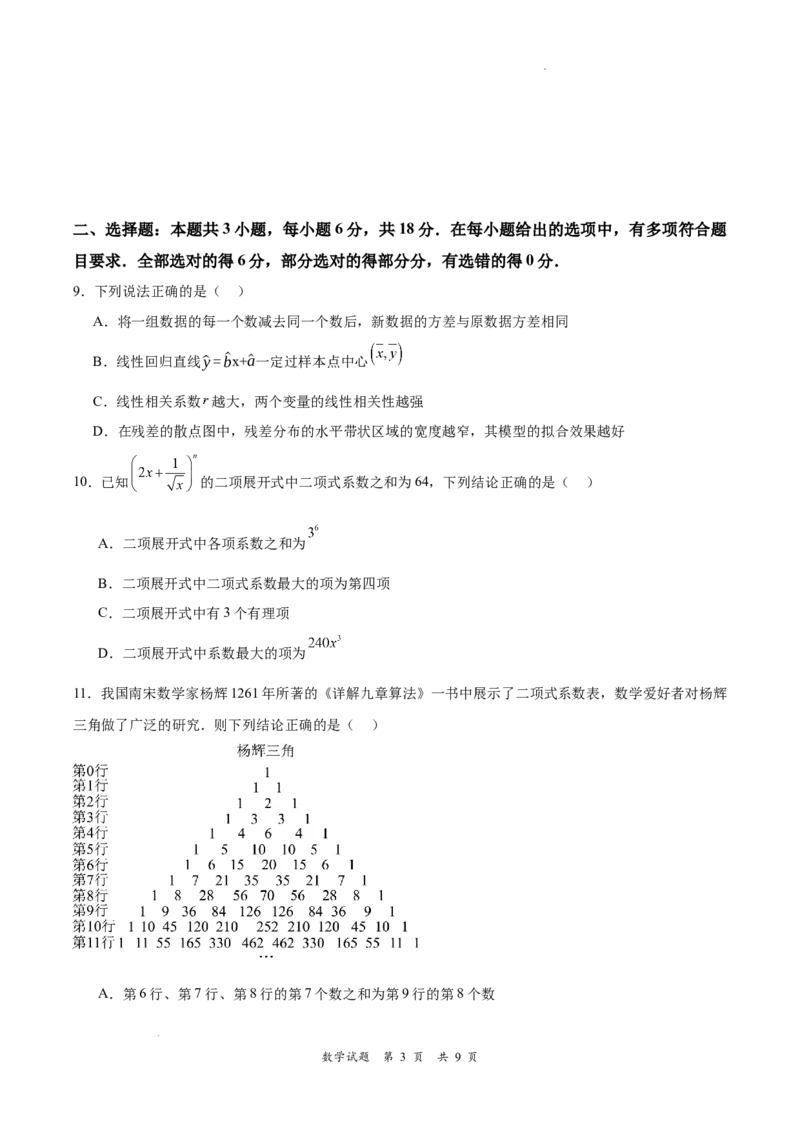
11.我国南宋数学家杨辉1261年所著的《详解九章算法》一书中展示了二项式系数表,数学爱好者对杨辉
三角做了广泛的研究.则下列结论正确的是( )
A.第6行、第7行、第8行的第7个数之和为第9行的第8个数
数学试题 第 3 页 共 9 页
学科网(北京)股份有限公司B.
C.第2020行的第1010个数最大
D.第12行中从左到右第2个数与第3个数之比为
第 Ⅱ 卷
(非选择题,共92分)
三、填空题:本题共3小题,每小题5分,共15分.
12.若 展开式中的常数项为 ,则实数 .
13.某植物园要在如图所示的5个区域种植果树,现有5种不同的果树供选择,要求相邻区域不能种同一
种果树,则共有 种不同的方法.
14.“冰天雪地也是金山银山”,2023-2024年雪季,东北各地冰雪旅游呈现出一片欣欣向荣的景象,为
东北经济发展增添了新动能.某市以“冰雪童话”为主题打造—圆形“梦幻冰雪大世界”,其中共设“森
林姑娘”“扣像墙”“古堡滑梯”等16处打卡景观.若这16处景观分别用 表示,某游客按照
箭头所示方向(不可逆行)可以任意选择一条路径走向其它景观,并且每个景观至多经过一次,那么他从
入口出发,按图中所示方向到达 有 种不同的打卡路线;若该游客按上述规则从入口出发到达
景观 的不同路线有 条,其中 ,记 ,则 (结果
用 表示).
数学试题 第 4 页 共 9 页
学科网(北京)股份有限公司四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)设(1−2x) 5=a +a x+a x2 +.....+ a x5 .
0 1 2 5
(1)求 的值;
(2)求 的值.
16.(15分)为提高学生的数学应用能力和创造力,学校打算开设“数学建模”选修课,为了解学生对“数
学建模”的兴趣度是否与性别有关,学校随机抽取该校30名高中学生进行问卷调查,其中认为感兴趣的人
数占 .
(1)根据所给数据,完成下面的 列联表,并根据列联表判断,依据小概率值 的独立性检验,分析
学生对“数学建模”选修课的兴趣度与性别是否有关?
感兴趣 不感兴趣 合计
男
12
生
女
5
生
合
30
计
(2)若感兴趣的女生中恰有4名是高三学生,现从感兴趣的女生中随机选出3名进行二次访谈,记出高三女
生的人数为 ,求 的分布列与数学期望.
附: ,其中 ;
0.10 0.05 0.01 0.005 0.001
数学试题 第 5 页 共 9 页
学科网(北京)股份有限公司2.706 3.841 6.635 7.879 10.828
17.(15分)全球新能源汽车产量呈上升趋势.以下为 年全球新能源汽车的销售量情况统计.
201
年份 2018 2020 2021 2022 2023
9
年份编号 1 2 3 4 5 6
销售量 /百万辆 2.02 2.21 3.13 6.70 10.80 14.14
若 与 的相关关系拟用线性回归模型表示,回答如下问题:
(1)求变量 与 的样本相关系数 (结果精确到0.01);
(2)求 关于 的线性回归方程,并据此预测2024年全球新能源汽车的销售量.
附:线性回归方程 ,其中 ,
样本相关系数 .
参考数据: .
数学试题 第 6 页 共 9 页
学科网(北京)股份有限公司18.(17分)梅河口市第五中学一研究性学习小组为了解梅河口市市民每年旅游消费支出费用(单位:千
元),春节期间对游览某网红景区的100名梅河口市游客进行随机问卷调查,并把数据整理成如下表所示
的频数分布表:
组别(支出费用)
频数 3 4 8 11 41 20 8 5
(1)从样本中随机抽取两位市民的支出数据,求两人旅游支出不低于10000元的概率;
(2)若市民的旅游支出费用X近似服从正态分布 , 近似为样本平均数 (同一组中的数据用该组
区间的中间值代表), 近似为样本标准差s,并已求得 ,利用所得正态分布模型解决以下问题:
①假定梅河口市常住人口为300万人,试估计梅河口市有多少市民每年旅游费用支出在15000元以上;
②若在梅河口市随机抽取3位市民,设其中旅游费用在9000元以上的人数为 ,求随机变量的 分布列和
均值.
附:若 ,则 , ,
数学试题 第 7 页 共 9 页
学科网(北京)股份有限公司19.(17分)为进一步培养高中生数学学科核心素养,提高创造性思维和解决实际问题的能力,某省举办高
中生数学建模竞赛现某市从M,N两个学校选拔学生组队参赛,M,N两个学校学生总数分别为1989人、
3012人.两校分别初选出4人、6人用于组队参赛,其中两校选拔的人中各有两人有比赛经验,按照分层
抽样从M,N两个学校初选人中共选择5名学生组队参赛,设该队5人中有参赛经验的人数为X.
(1)求随机变量X的分布列及数学期望 ;
(2)各市确定5人组队参赛,此次比赛规则是:小组内自行指定一名同学起稿建立模型,之后每轮进行两人
单独交流.假设某队决定由A起稿建立模型,A从其他四名成员中选择一人B进行交流,结束后把成果交
由B,然后B再从其他包括A在内的四个成员中选择一人进行交流 每一个环节只能是两名成员单独交
流,每个小组有20次交流机会,最后再进入评委打分环节,现该市选定甲、乙、丙、丁、戊五人参赛,其
中甲、乙两人有参赛经验.在每次交流中,甲、乙被同伴选为交流对象的概率均为 ,丙、丁、戊被同伴
选为交流对象的概率相等,比赛由甲同学起稿建立模型.
①求该组第三次交流中甲被选择的概率;
②求第n次交流中甲被选择的概率( , ).
数学试题 第 8 页 共 9 页
学科网(北京)股份有限公司数学试题 第 9 页 共 9 页
学科网(北京)股份有限公司