文档内容
广东省茂名市5 2校际联盟2024-2025学年高二下学期质量检测数学试题
一、单选题
1.已知函数 在 处可导,且 ,则 ( )
A. B.0 C.1 D.2025
2.首项为3的等差数列 满足 ,则 的公差为( )
A.1 B.2 C.3 D.4
3.已知某同学参加了当地相关部门举办的数学奥林匹克竞赛的预赛,该预赛共有3道解答题,3道全部答
对即可获得满分,已知该同学答对这3道解答题的概率依次为0.8, ,则该同学按题号顺序连续正
确解答出2道解答题但没获得满分的概率为( )
A.0.408 B.0.384 C.0.246 D.0.532
4.已知椭圆 的离心率为 ,则 的短轴长为( )
A. B.1 C.2 D.4
5. 年 月 日,冰雪同梦绽放光芒,亚洲同心共谱华章.第九届亚洲冬季运动会在黑龙江省哈尔滨
市隆重开幕,在本次滑雪比赛中,某摄影师利用雷达干涉仪记录了某名运动员整个过程中由起点起经过
秒后的位移 (单位:米)与时间 (单位:秒)的关系为 ,则该名运动员在滑雪过程中
瞬时速度为零的时刻为( )
A.1秒末 B.2秒末 C.4秒末 D.1秒末和4秒末
6.已知点 , ,若以 为圆心,5为半径的圆与线段 的垂直平分线相切,则
( )
A. B. 或 C. D. 或
7.已知数列 和数列 满足 , ,则下列数列为等差数列的是( )A. B. C. D.
8.已知正三棱锥 的三个侧面均为等腰直角三角形,过点 作一平面使得 三点在该平面的
同一侧,且 三点到该平面的距离分别为 ,则三棱锥 的侧棱长为( )
A.3 B. C. D.4
二、多选题
9.下列函数求导运算正确的是( )
A. B.
C. D.
10.在一个密闭的盒子中放有大小和形状都相同,编号分别为 的4张卡牌,现从中依次不放回摸出
两张卡牌,记事件 “第一次摸出的卡牌的编号为奇数”,事件 “摸出的两张卡牌的编号之和为
5”,事件 “摸出的两张卡牌中有编号为2的卡牌”,则( )
A. B.事件 与事件 相互独立
C. D.事件 与事件 为互斥事件
11.记 为正项数列 的前 项和, 为 的前 项积,已知 ,则( )
A. B. 可能为常数列
C. D.
三、填空题
12.已知空间向量 , ,若 ,则 .
13.已知函数 在点 处的切线斜率为 ,则曲线 在点 处的切线方程为 .
14.已知双曲线 的上焦点为 ,以 轴上一动点为圆心,半径为 的圆与 的上支交于 、
两点,则点 到 、 两点距离之和的最小值为 .
四、解答题
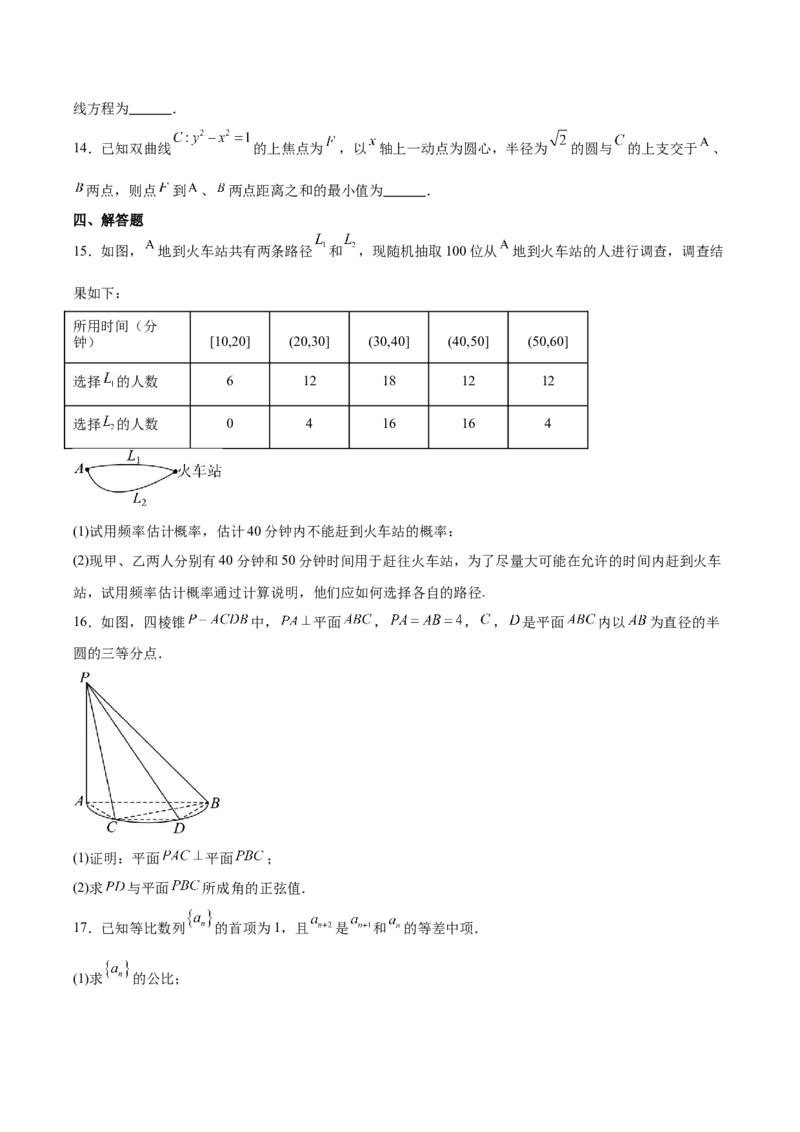
15.如图, 地到火车站共有两条路径 和 ,现随机抽取100位从 地到火车站的人进行调查,调查结
果如下:
所用时间(分
钟) [10,20] (20,30] (30,40] (40,50] (50,60]
选择 的人数 6 12 18 12 12
选择 的人数 0 4 16 16 4
(1)试用频率估计概率,估计40分钟内不能赶到火车站的概率:
(2)现甲、乙两人分别有40分钟和50分钟时间用于赶往火车站,为了尽量大可能在允许的时间内赶到火车
站,试用频率估计概率通过计算说明,他们应如何选择各自的路径.
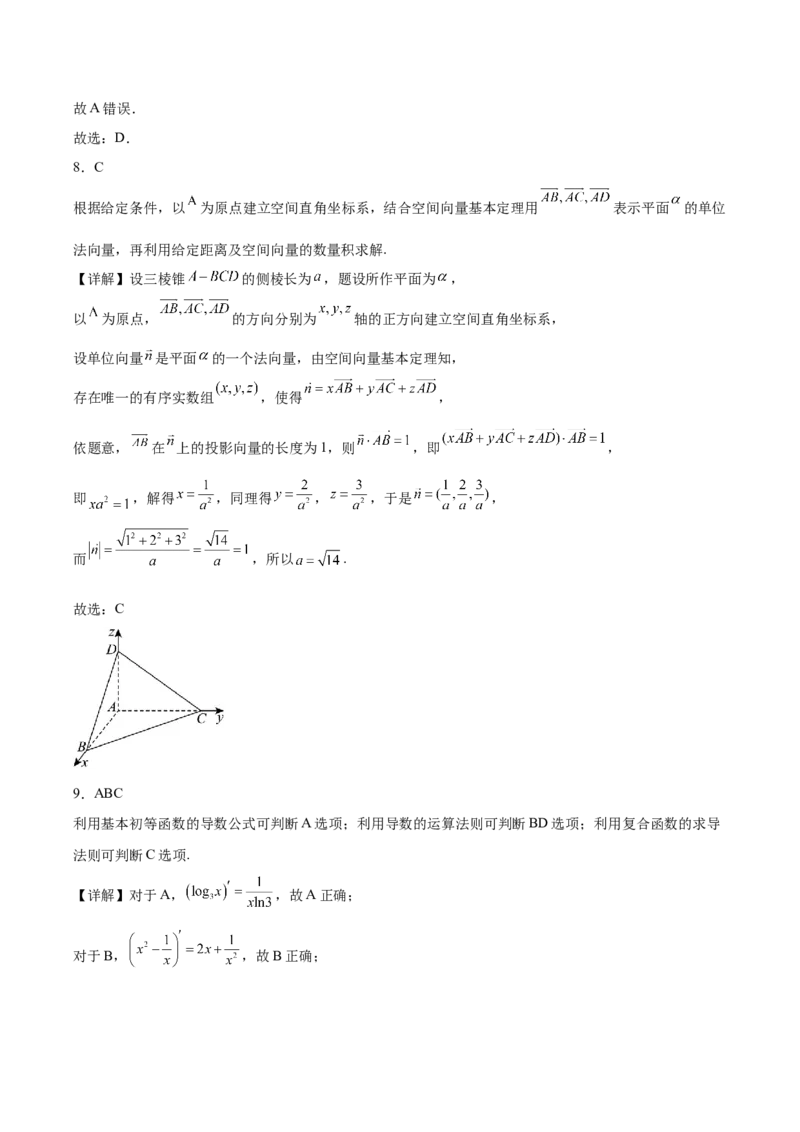
16.如图,四棱锥 中, 平面 , , , 是平面 内以 为直径的半
圆的三等分点.
(1)证明:平面 平面 ;
(2)求 与平面 所成角的正弦值.
17.已知等比数列 的首项为1,且 是 和 的等差中项.
(1)求 的公比;(2)求数列 的前 项和 .
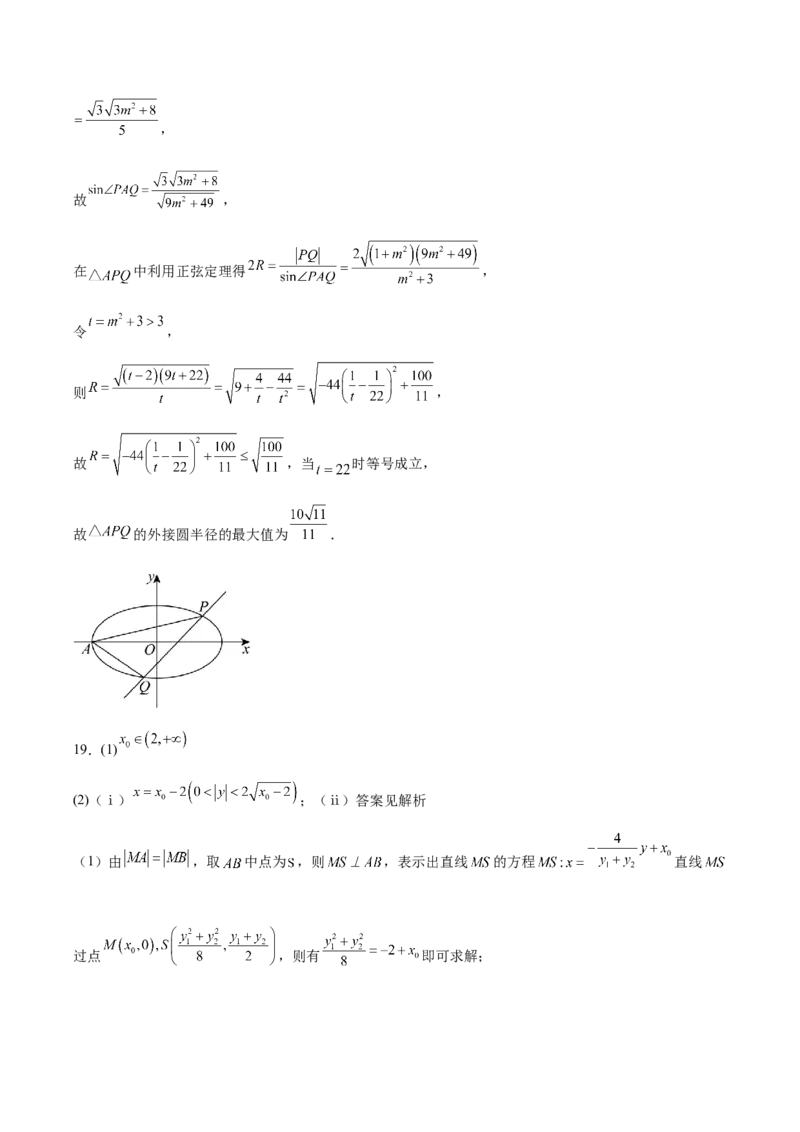
18.已知椭圆 的左顶点为 ,过点 的直线 交 于 两点.
(1)当 斜率不存在时,求 外接圆的半径;
(2)求 外接圆的半径的最大值.
19.对于在 轴上的一点 ,若以 轴为对称轴的抛物线 上存在两点 使得 ,且
不与 轴垂直,则称线段 是抛物线 的一条“ —伴随线段”.
(1)若抛物线 存在“ —伴随线段”,求 的取值范围;
(2)给定 使得抛物线 存在“ —伴随线段”.
(ⅰ)求“ —伴随线段”的中点的轨迹方程;
(ⅱ)讨论“ —伴随线段”的长度是否有最大值,若有,求出最大值(用 表示);若没有,说明理由.题号 1 2 3 4 5 6 7 8 9 10
答案 A B A B C B D C ABC BC
题号 11
答案 ABC
1.A
由导数的定义得 .
【详解】因为 ,
所以由导数的定义可知 ,
故选:A.
2.B
根据等差数列得到关于公差 的方程 ,解得 .
【详解】设等差数列 的公差为 ,由题意可得 , ,所以 ,解得
.
故选:B.
3.A
应用互斥事件概率及独立事件乘法公式计算即可.
【详解】由题意可得所求事件的概率为 .
故选:A.
4.B
依据椭圆 计算 的范围,确定焦点在 轴上,再计算离心率,建立等式关系.
【详解】依题意, ,即 ,则椭圆 的焦点在 轴上,因此 ,所以
,故椭圆 的短轴长为 .
故选:B.
5.C根据条件,利用导数的物理意义得 ,即可求解.
【详解】因为 ,所以 ,
令 ,得 ,解得 或 (舍去).
故选:C.
6.B
根据中点坐标公式和斜率公式求出线段AB的中点坐标和斜率,进而得到其垂直平分线的方程.再利用直线
与圆相切时圆心到直线的距离等于半径这一性质,结合点到直线的距离公式列出关于 的方程,最后求解
方程得到 的值.
【详解】线段 中点 , 斜率: ,
则垂直平分线 ,整理得 ,
相切即圆心到直线的距离等于半径,由点到直线的距离公式有, ,
即 ,解得 或 .
故选:B.
7.D
根据等差数列的定义逐一判断即可.
【详解】依题意,对 消去 ,得 ,等价于 ,所以
,
所以 是等差数列,故D正确,C错误;若 是等差数列,则 是等差数列,则 是等差
数列,
与 是公差为1的等差数列矛盾,故B错误;因为 ,故A错误.
故选:D.
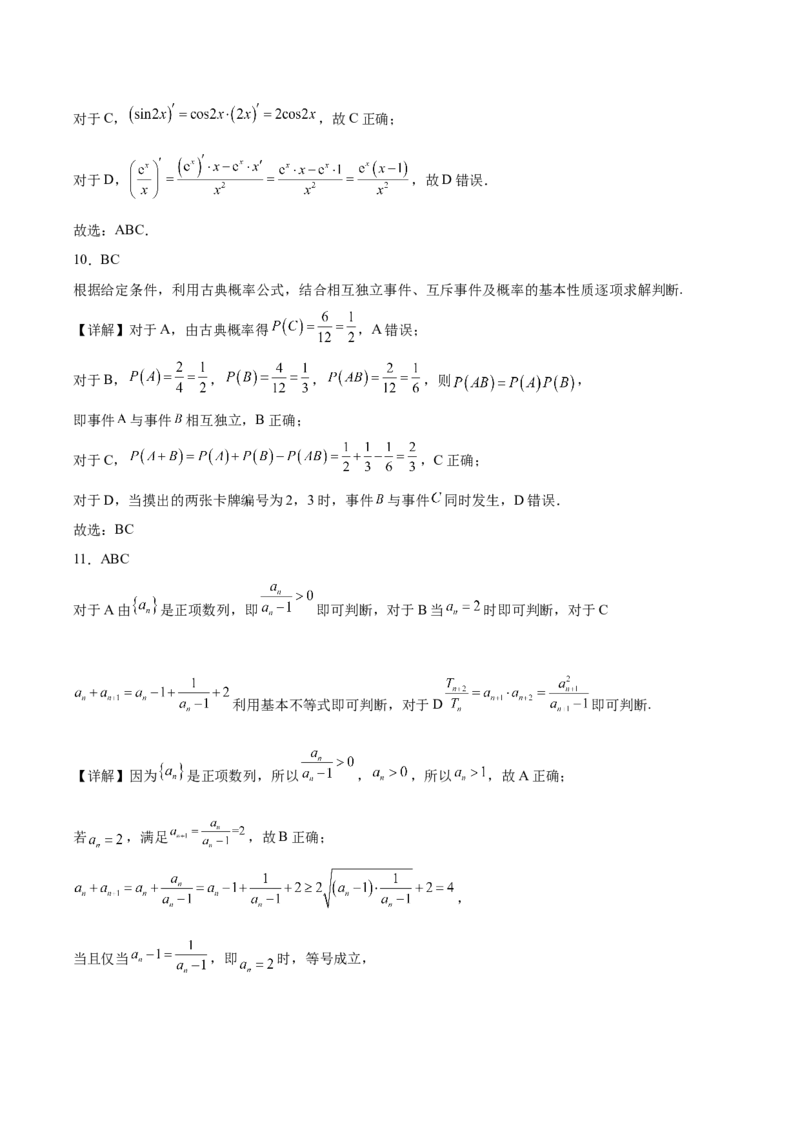
8.C
根据给定条件,以 为原点建立空间直角坐标系,结合空间向量基本定理用 表示平面 的单位
法向量,再利用给定距离及空间向量的数量积求解.
【详解】设三棱锥 的侧棱长为 ,题设所作平面为 ,
以 为原点, 的方向分别为 轴的正方向建立空间直角坐标系,
设单位向量 是平面 的一个法向量,由空间向量基本定理知,
存在唯一的有序实数组 ,使得 ,
依题意, 在 上的投影向量的长度为1,则 ,即 ,
即 ,解得 ,同理得 , ,于是 ,
而 ,所以 .
故选:C
9.ABC
利用基本初等函数的导数公式可判断A选项;利用导数的运算法则可判断BD选项;利用复合函数的求导
法则可判断C选项.
【详解】对于A, ,故A正确;
对于B, ,故B正确;对于C, ,故C正确;
对于D, ,故D错误.
故选:ABC.
10.BC
根据给定条件,利用古典概率公式,结合相互独立事件、互斥事件及概率的基本性质逐项求解判断.
【详解】对于A,由古典概率得 ,A错误;
对于B, , , ,则 ,
即事件 与事件 相互独立,B正确;
对于C, ,C正确;
对于D,当摸出的两张卡牌编号为2,3时,事件 与事件 同时发生,D错误.
故选:BC
11.ABC
对于A由 是正项数列,即 即可判断,对于B当 时即可判断,对于C
利用基本不等式即可判断,对于D 即可判断.
【详解】因为 是正项数列,所以 , ,所以 ,故A正确;
若 ,满足 ,故B正确;
,
当且仅当 ,即 时,等号成立,所以 ,
当且仅当 时,等号成立,故C正确;
,
即 ,故D错误.
故选:ABC.
12. / /
由 得 ,即可得到 的值.
【详解】因为 ,所以 ,解得 .
故答案为: .
13.
根据条件,利用导数的几可意义,即可求解.
【详解】由题意可得 ,故 ,则 ,
又 ,所以 ,
故曲线 在点 处的切线方程为 ,化简可得 ,
故答案为: .
14.
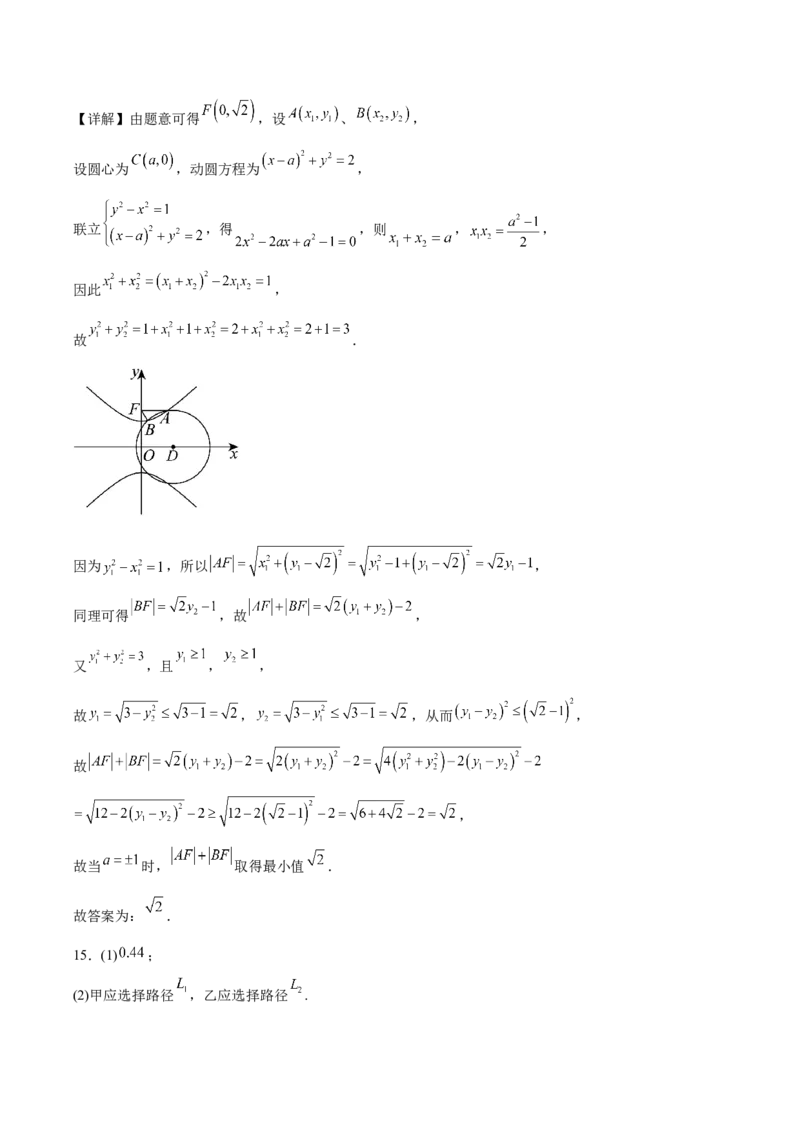
设出圆的方程与双曲线方程联立,可得 、 ,进而可得 ,利用两点间距离公式求出
,并利用不等式方法求出其最小值.【详解】由题意可得 ,设 、 ,
设圆心为 ,动圆方程为 ,
联立 ,得 ,则 , ,
因此 ,
故 .
因为 ,所以 ,
同理可得 ,故 ,
又 ,且 , ,
故 , ,从而 ,
故
,
故当 时, 取得最小值 .
故答案为: .
15.(1) ;
(2)甲应选择路径 ,乙应选择路径 .(1)根据频数计算频率即可;
(2)分别计算两个时间段的概率,比较概率的大小可得结论.
【详解】(1)调查的100人,其中40分钟内不能赶到火车站有: (人),
因此40分钟内不能赶到火车站的频率为 ,
用频率估计概率,所以40分钟内不能赶到火车站的概率为 .
(2)设 分别表示甲选择 和 时,在40分钟内赶到火车站;
分别表示乙选择 和 时,在50分钟内赶到火车站,
依题意, , ,
由 ,得甲应选择路径 ;
, ,
由 ,得乙应选择路径 ,
所以甲应选择路径 ,乙应选择路径 .
16.(1)证明见解析
(2) .
(1)先应用线面垂直判定定理得出 平面 ,再应用面面垂直判定定理证明即可;
(2)先建立空间直角坐标系,先求平面 的一个法向量,再应用线面角正弦公式计算即可.
【详解】(1)因为 平面 , 平面 ,所以 ,
因为 是平面 内以 为直径的半圆的三等分点,
所以 ,所以 ,所以 ,
因为 , 平面 , 平面 ,所以 平面 ,
又因为 平面 ,所以平面 平面PBC.
(2)以 为坐标原点,垂直于 的方向为 轴正方向, 的方向分别为 轴, 轴正方向,
建立如图所示的空间直角坐标系 ,则 , , , , ,
故 , , ,
设平面 的一个法向量为 ,
则 ,可以取 ,
设直线 与平面 所成角为 ,
所以 ,
故 与平面 所成角的正弦值为 .
17.(1)证明见解析
(2)
(1)应用等差中项列式,再计算求解公比;
(2)分公比为1或 分别应用等差数列求和公式及错位相减法计算求解.
【详解】(1)由题意可得 ,
设 的公比为 ,则 , ,
即 ,由题可知 ,也即 ,
解得 或 ,即 的公比为1或 .
(2)当公比为1时, 为常数列,且首项为1,即 ,
则 ,
则数列 的前 项和 .
当公比为 时,此时 ,则 ,
则数列 的前 项和 ,
,
两式相减可得 ,
即 ,也即 .
综上, .
18.(1)
(2)
(1)求出点 坐标,利用对称性可设外心 ,利用 建立方程关系即可得出半径;(2)设直线方程,联立方程组,求出 以及利用斜率得出 ,进而得出 ,
在 中利用正弦定理可计算外接圆半径.
【详解】(1)由题意可知直线 ,
联立 ,解得 ,
不妨设 , ,易得此时 外接圆圆心 在 轴上, ,设 ,
则 的外接圆半径 ,即 ,
解得 ,故 .
(2)当直线 与 轴重合时无法构成三角形,
则设 , , ,
联立 ,得
则 , , ,
则
,
, ,易得,
故 ,
在 中利用正弦定理得 ,
令 ,
则 ,
故 ,当 时等号成立,
故 的外接圆半径的最大值为 .
19.(1)
(2)(ⅰ) ;(ⅱ)答案见解析
(1)由 ,取 中点为 ,则 ,表示出直线 的方程 直线
过点 ,则有 即可求解;(2)(ⅰ)由 得中点 的横坐标为 ,即 的横坐标在定直线 上,
又 与直线 交点为 即可求解;(ⅱ)由两点的距离公式有
,利用基本不等式有 ,可得 ,解得
,把 看成关于 的二次函数,最后利用
二次函数的性质即可求解.
【详解】(1)由 ,取 中点为 ,则 .
设 , ,则直线 斜率的倒数为 ,
则直线 斜率的倒数为 ,设 ,
因其过点 ,代入得 ,
又 ,故则 .
(2)(ⅰ)由(1)得 ,又中点 的横坐标为 ,故点 在定直线 上;
又 与直线 交点为 ,显然中点纵坐标绝对值小于 ,
又 不与 轴垂直,故 ,故轨迹方程为 .
(ⅱ),
因 ,当且仅当 时等号成立.
又 的斜率存在且不为0,所以 ,
故 ,解得 , ,
又 可看成关于 的二次函数,且当且仅当 取最大值 ,
当 即 时,弦长有最大值 ,当且仅当 取等号;
当 时, ,则无最大值;
综上所述, 时弦长无最大值, 时弦长有最大值 .