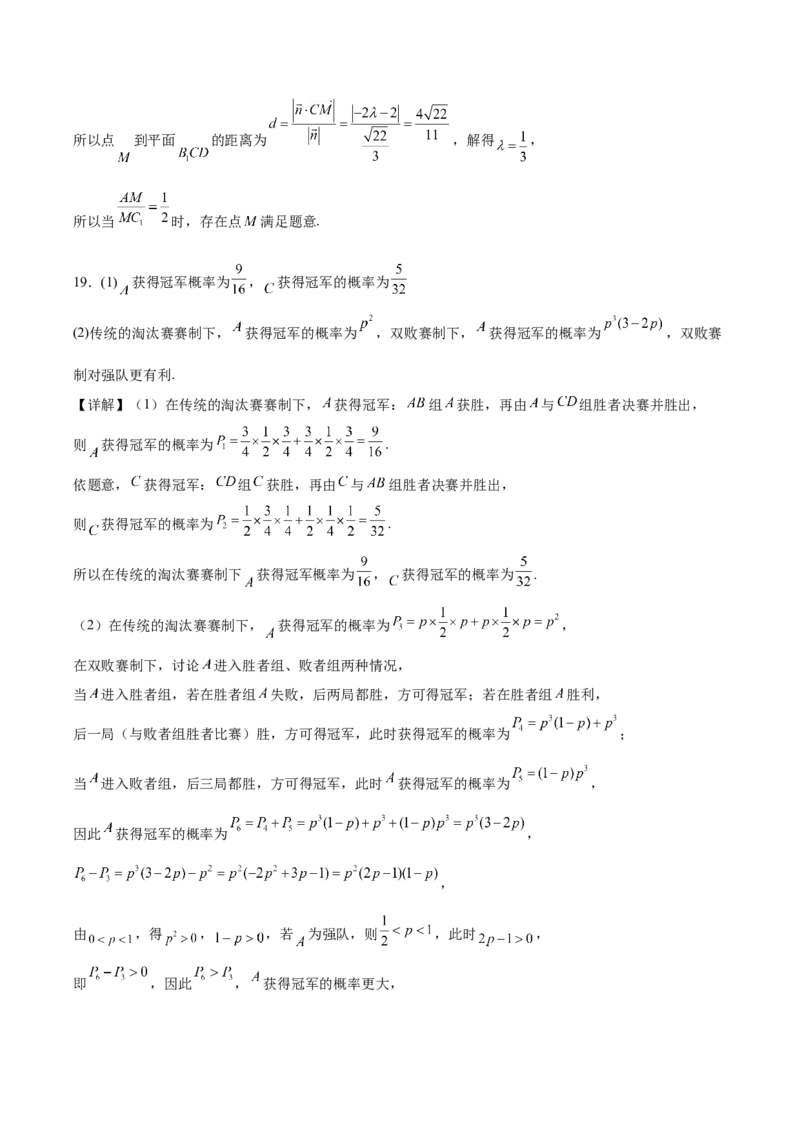文档内容
广东省茂名市信宜市2025-2026学年高二上学期11月期中
数学试题
一、单选题
1.为了了解某地区5000名小学生的体育素质情况,从中抽取了500名小学生进行测试,该地区每位小学
生被抽到的可能性为( )
A. B. C. D.
2.直线 的倾斜角为( )
A. B. C. D.
3.样本数据32、22、42、29、34、47、37、38、45、51、49、53的下四分位数(25%分位数)为( )
A.32 B.33 C.48 D.49
4.已知数据3,7,4,7, ,6的平均数是5,则这组数据的方差为( )
A.3 B. C.5 D.
5.将直线 : 绕其与 轴的交点旋转 得到直线 ,则直线 的方程是( )
A. B. C. D.
6.已知直线 : , : ,若 ,则 的值是( )
A. 或 B. C. D.
7.如图,三个自动开关 , , 正常工作的概率都是 ,且是互相独立的.若将它们接入电路中,则电
路不发生故障的概率是( )
A. B. C. D.8.已知 , , ,则事件 与 的关系是( )
A. 与 互斥不对立 B. 与 对立
C. 与 相互独立 D. 与 既互斥又独立
二、多选题
9.已知向量 , , ,则下列结论正确的是( )
A. B. C. D.
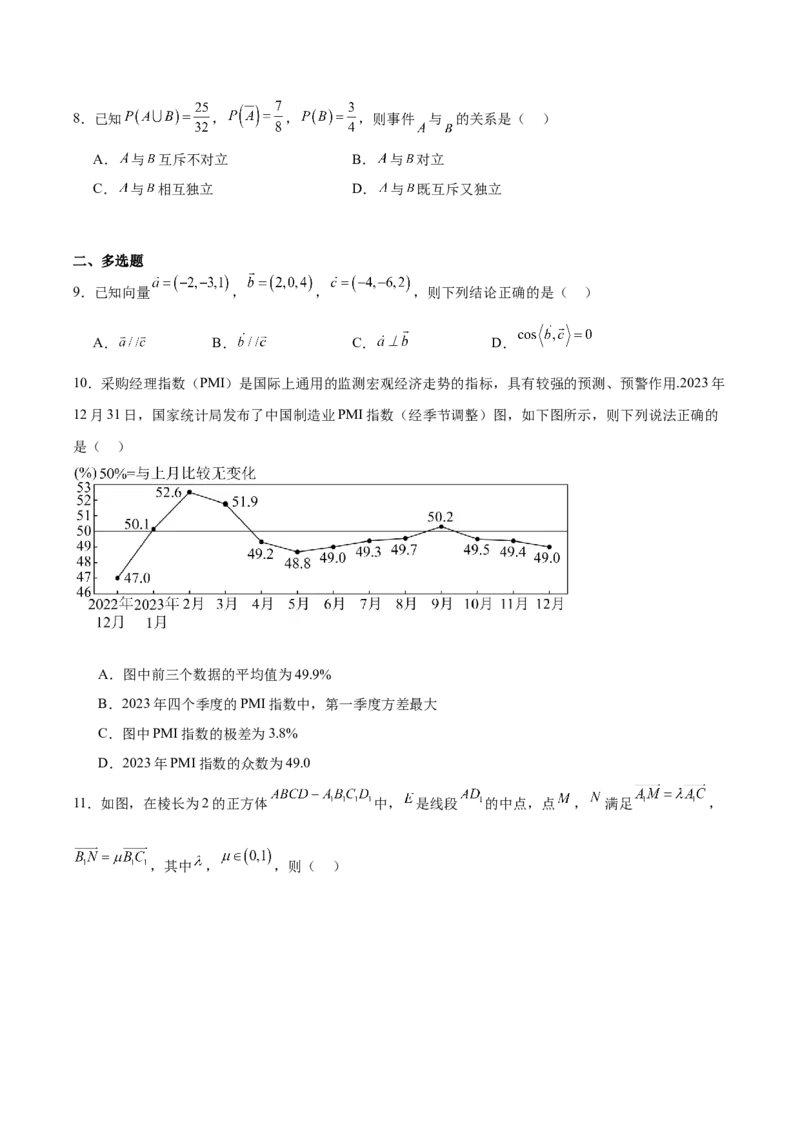
10.采购经理指数(PMI)是国际上通用的监测宏观经济走势的指标,具有较强的预测、预警作用.2023年
12月31日,国家统计局发布了中国制造业PMI指数(经季节调整)图,如下图所示,则下列说法正确的
是( )
A.图中前三个数据的平均值为49.9%
B.2023年四个季度的PMI指数中,第一季度方差最大
C.图中PMI指数的极差为3.8%
D.2023年PMI指数的众数为49.0
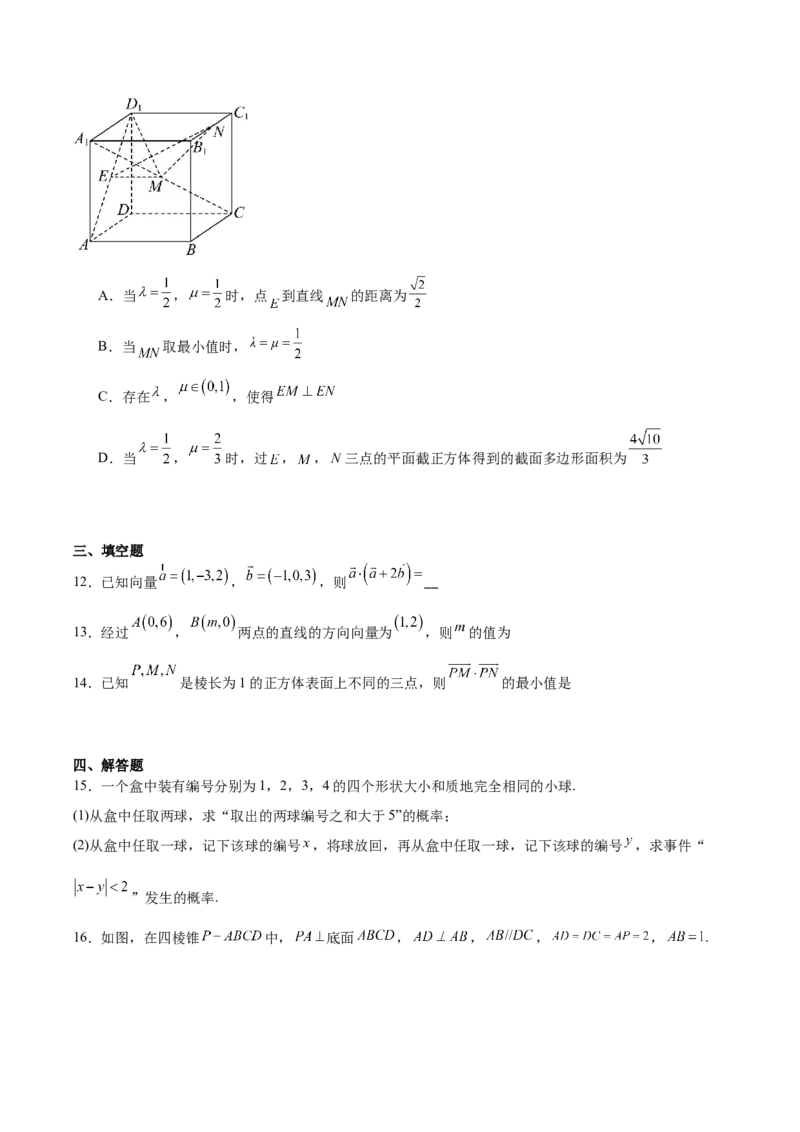
11.如图,在棱长为2的正方体 中, 是线段 的中点,点 , 满足 ,
,其中 , ,则( )A.当 , 时,点 到直线 的距离为
B.当 取最小值时,
C.存在 , ,使得
D.当 , 时,过 , , 三点的平面截正方体得到的截面多边形面积为
三、填空题
12.已知向量 , ,则
13.经过 , 两点的直线的方向向量为 ,则 的值为
14.已知 是棱长为1的正方体表面上不同的三点,则 的最小值是
四、解答题
15.一个盒中装有编号分别为1,2,3,4的四个形状大小和质地完全相同的小球.
(1)从盒中任取两球,求“取出的两球编号之和大于5”的概率;
(2)从盒中任取一球,记下该球的编号 ,将球放回,再从盒中任取一球,记下该球的编号 ,求事件“
”发生的概率.
16.如图,在四棱锥 中, 底面 , , , , .(1)求 与平面 所成角的正弦值;
(2)求证:平面 平面
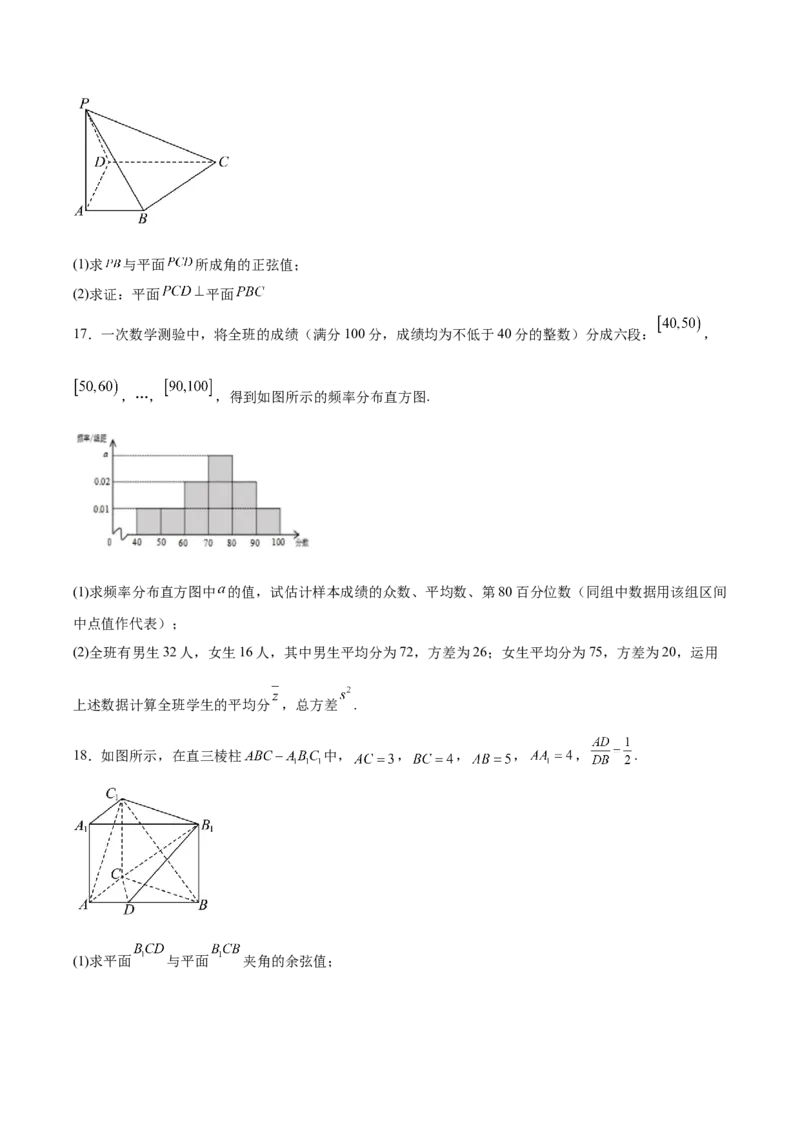
17.一次数学测验中,将全班的成绩(满分100分,成绩均为不低于40分的整数)分成六段: ,
,…, ,得到如图所示的频率分布直方图.
(1)求频率分布直方图中 的值,试估计样本成绩的众数、平均数、第80百分位数(同组中数据用该组区间
中点值作代表);
(2)全班有男生32人,女生16人,其中男生平均分为72,方差为26;女生平均分为75,方差为20,运用
上述数据计算全班学生的平均分 ,总方差 .
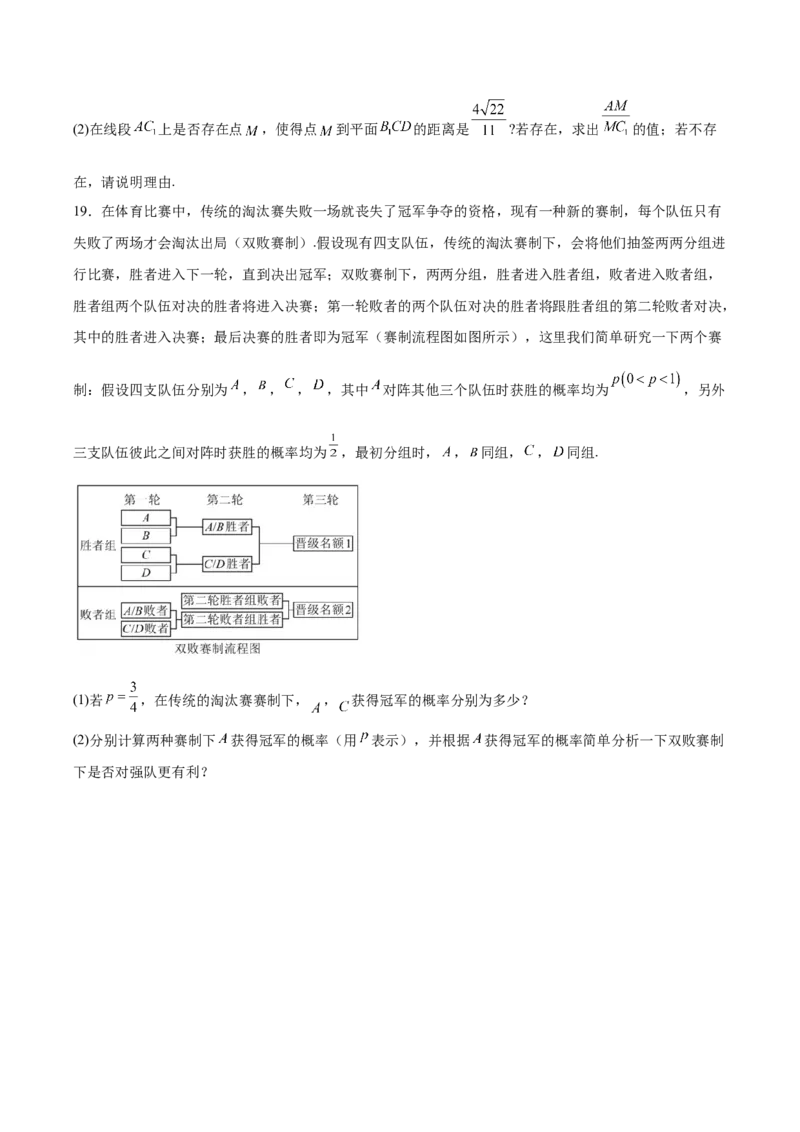
18.如图所示,在直三棱柱 中, , , , , .
(1)求平面 与平面 夹角的余弦值;(2)在线段 上是否存在点 ,使得点 到平面 的距离是 ?若存在,求出 的值;若不存
在,请说明理由.
19.在体育比赛中,传统的淘汰赛失败一场就丧失了冠军争夺的资格,现有一种新的赛制,每个队伍只有
失败了两场才会淘汰出局(双败赛制).假设现有四支队伍,传统的淘汰赛制下,会将他们抽签两两分组进
行比赛,胜者进入下一轮,直到决出冠军;双败赛制下,两两分组,胜者进入胜者组,败者进入败者组,
胜者组两个队伍对决的胜者将进入决赛;第一轮败者的两个队伍对决的胜者将跟胜者组的第二轮败者对决,
其中的胜者进入决赛;最后决赛的胜者即为冠军(赛制流程图如图所示),这里我们简单研究一下两个赛
制:假设四支队伍分别为 , , , ,其中 对阵其他三个队伍时获胜的概率均为 ,另外
三支队伍彼此之间对阵时获胜的概率均为 ,最初分组时, , 同组, , 同组.
(1)若 ,在传统的淘汰赛赛制下, , 获得冠军的概率分别为多少?
(2)分别计算两种赛制下 获得冠军的概率(用 表示),并根据 获得冠军的概率简单分析一下双败赛制
下是否对强队更有利?参考答案
1.A
【详解】该地区每位小学生被抽到的可能性为 ,
故选:A
2.B
【详解】设直线 的倾斜角为 ,且 ,
则 ,所以 .
故选:B
3.B
【详解】样本数据从小到大排列为22、29、32、34、37、38、42、45、47、49、51、53,
因为 ,所以下四分位数(25%分位数)为第三个数和第四个数的平均数 .
故选:B.
4.A
【详解】由条件可知, ,得 ,
这组数据的方差 .
故选:A
5.B
【详解】由条件可知, 与 轴的交点为 ,且斜率为 ,因为 ,所以直线 的斜率为 ,所以
直线 的方程是 ,整理为 .
故选:B
6.D
【详解】因为直线 : , : ,且 ,
所以 ,解得 ,
故选:D7.D
【详解】记“三个元件 , , 正常工作”分别为事件 , , ,则 , ,
.
不发生故障的事件为 ,
∴不发生故障的概率为 .
故选:D
8.C
【详解】由 可得 ,
因为 ,则 与 不互斥,不对立,
由 可得 ,
因为 ,所以 与 相互独立
故选:C
9.ACD
【详解】向量 , , ,
因为 ,所以 ,A选项正确;
易知不存在实数 使得 ,所以 不平行,B选项错误;
显然 ,所以 ,C选项正确;
易知 ,D选项正确;
故选:ACD.
10.ABD【详解】对于A,前三个数据为 , , ,所以前三个数据的平均值为
,故A选项正确;
对于B,从表中数据可以看出2023年四个季度的PMI指数中,第一季度的波动性最大,稳定性最差,所
以方差最大,故B选项正确;
对于C,图中PMI指数的最大值为 %,最小值为 %,故极差为 %,C选项错误;
对于D,2023年PMI指数中,49.0出现两次,其他的出现一次,故2023年PMI指数的众数为49.0,故D选
项正确.
故选:ABD
11.ABD
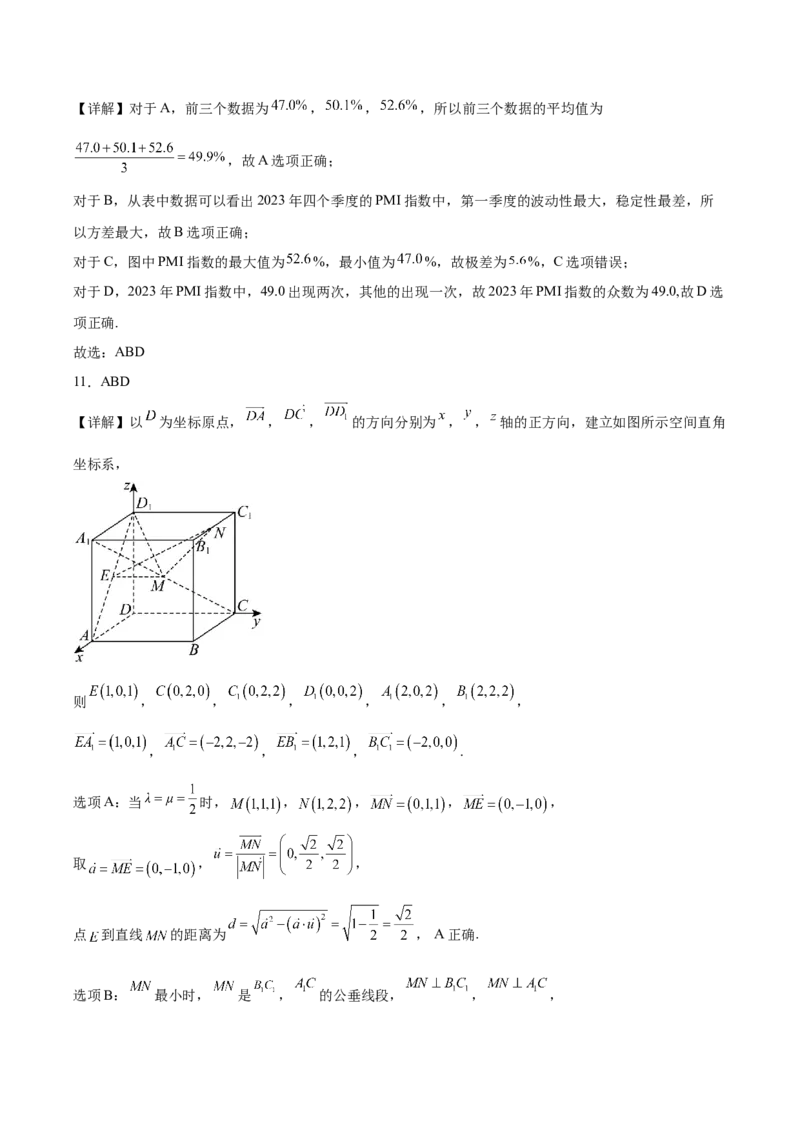
【详解】以 为坐标原点, , , 的方向分别为 , , 轴的正方向,建立如图所示空间直角
坐标系,
则 , , , , , ,
, , , .
选项A:当 时, , , , ,
取 , ,
点 到直线 的距离为 , A正确.
选项B: 最小时, 是 , 的公垂线段, , ,,
,解得 , B正确.
选项C: ,
,
若 ,则 ,即 ,
因为 , ,显然 ,所以 不成立,C错误;
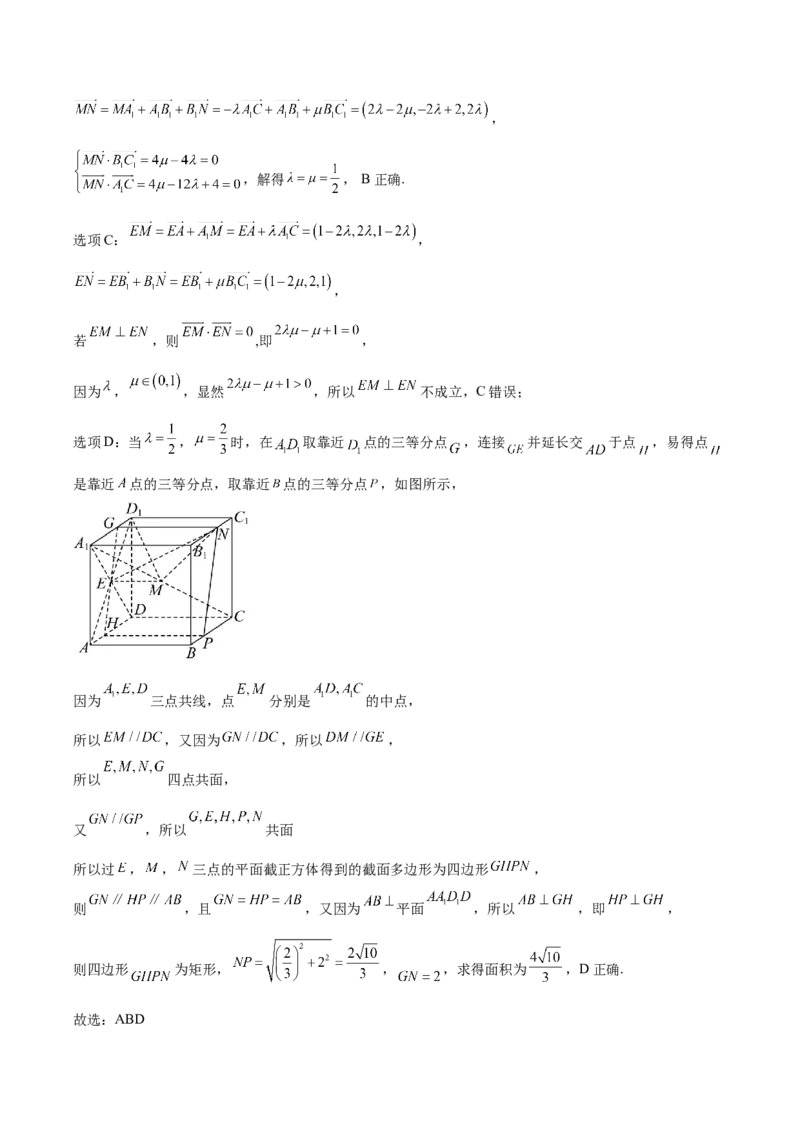
选项D:当 , 时,在 取靠近 点的三等分点 ,连接 并延长交 于点 ,易得点
是靠近 点的三等分点,取靠近 点的三等分点 ,如图所示,
因为 三点共线,点 分别是 的中点,
所以 ,又因为 ,所以 ,
所以 四点共面,
又 ,所以 共面
所以过 , , 三点的平面截正方体得到的截面多边形为四边形 ,
则 ,且 ,又因为 平面 ,所以 ,即 ,
则四边形 为矩形, , ,求得面积为 ,D正确.
故选:ABD12.24
【详解】 ,
所以 .
故答案为:
13.
【详解】由条件可知直线 的斜率为2,所以 ,得 .
故答案为:
14. /
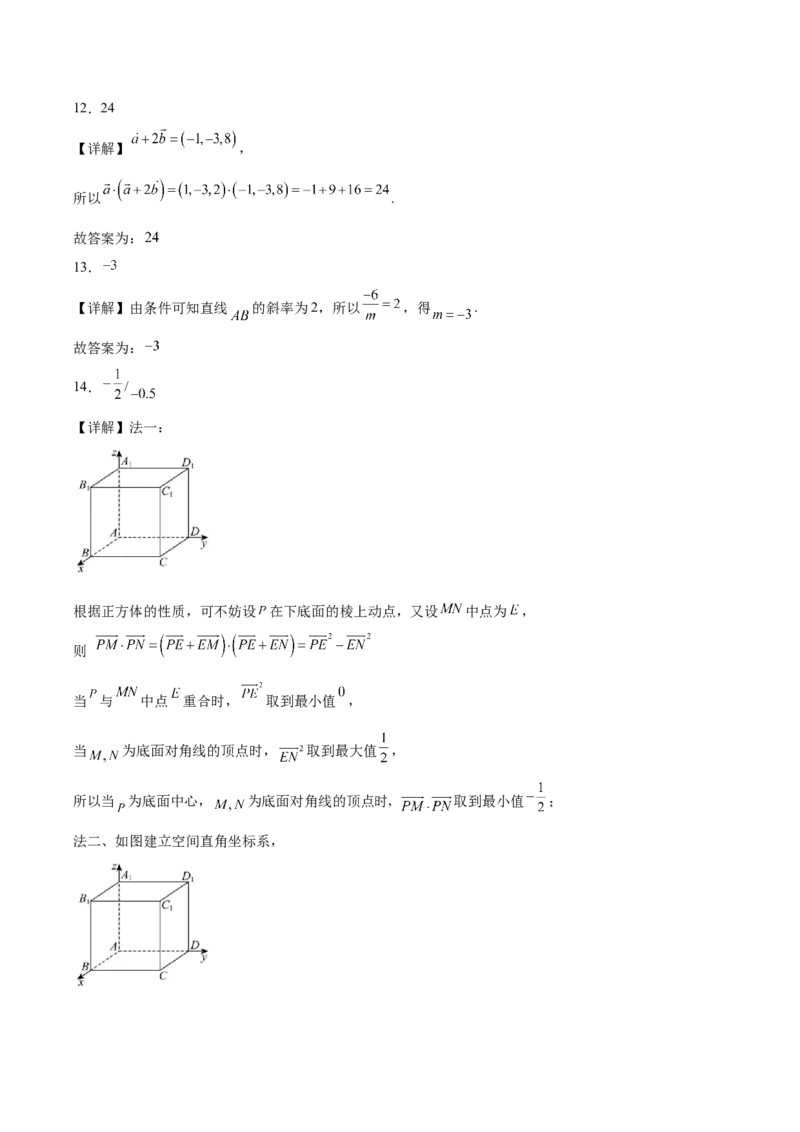
【详解】法一:
根据正方体的性质,可不妨设 在下底面的棱上动点,又设 中点为 ,
则
当 与 中点 重合时, 取到最小值 ,
当 为底面对角线的顶点时, 取到最大值 ,
所以当 为底面中心, 为底面对角线的顶点时, 取到最小值 ;
法二、如图建立空间直角坐标系,设 , , ,其中 , , .
则 , .
则
,
当 在正方体同一面上时,则当 , , 时, 取得最小值,
,
即当 为正方体一面的对角线, 为对角线中点时, 取得最小值 ;
当 、 、 不在正方体同一面上时,由对称性,不妨设 , , 不同时为0,
此时
;
因为 , , ,则 ,
所以 ,
综上, 的最小值是 .15.(1)
(2)
【详解】(1)从盒中任取两球的所有等可能基本事件有:
, , , , , ,共6个,
记取出的两球编号之和大于5的事件为 ,
则事件 包含, , 共2个等可能基本事件
所以 ;
所以取出的两球编号之和大于5的概率为 .
(2)有放回地连续抽取两球的所有等可能基本事件有:
, , , , , , , , , , , , , ,
, 共16个,
记 的事件为 ,
则事件 包含 , , , , , , , , , 共10个等可能基
本事件,
所以 ,
所以事件“ ”发生的概率为 .
16.(1)
(2)证明见解析【详解】(1)
依题意,以点 为原点, 所在直线分别为 轴、 轴、 轴,建立如图所示的 空间直
角坐标系.
则 , , , .
设平面 的一个法向量为 , ,
则 ,即
不妨令 ,可得 为平面 的一个法向量.
, ,
设 与平面 所成角为 ,则
(2)由(1)知 为平面 的一个法向量
设平面 的法向量 ,又向量 , ,
则 ,即 ,
不妨令 ,可得 为平面 的一个法向量.
因为 ,所以 .
所以平面 平面 .
17.(1) ,众数为75,平均数为72,第80百分位数为85
(2)平均分73,总方差26【详解】(1) 各组小矩形的面积之和为1,
所以
解得 .
由频率分布直方图可知:众数为75,
平均数为 .
设第80百分位数为 ,成绩在 的频率为 ,
成绩在 的频率为
所以 , ,
解得
故估计样本成绩的众数为75,平均数为72,第80百分位数为85.
(2)依题意,得两组成绩合并后的总平均数为 ,
总方差 .
故全班学生的平均分73,总方差26.
18.(1)
(2)存在,
【详解】(1)因为 , , ,所以 ,即 ,
在直三棱柱 中, 平面 ,
以 为坐标原点,直线 、 、 分别为 轴、 轴、 轴,建立如图所示的空间直角坐标系,则 , , , , , ,
所以 , ,
设平面 的法向量为 ,
则 ,令 ,得 ,则 ,
易知平面 的法向量为 ,则 ,
设平面 与平面 的夹角为 ,
所以 ,
所以平面 与平面 夹角的余弦值为 .
(2)假设线段 上存在点 ,使得点 到平面 的距离是 ,
由(1)知, ,设 , ,
所以 ,则 ,
由(1)知平面 的法向量为 , ,所以点 到平面 的距离为 ,解得 ,
所以当 时,存在点 满足题意.
19.(1) 获得冠军概率为 , 获得冠军的概率为
(2)传统的淘汰赛赛制下, 获得冠军的概率为 ,双败赛制下, 获得冠军的概率为 ,双败赛
制对强队更有利.
【详解】(1)在传统的淘汰赛赛制下, 获得冠军: 组 获胜,再由 与 组胜者决赛并胜出,
则 获得冠军的概率为 .
依题意, 获得冠军: 组 获胜,再由 与 组胜者决赛并胜出,
则 获得冠军的概率为 .
所以在传统的淘汰赛赛制下 获得冠军概率为 , 获得冠军的概率为 .
(2)在传统的淘汰赛赛制下, 获得冠军的概率为 ,
在双败赛制下,讨论 进入胜者组、败者组两种情况,
当 进入胜者组,若在胜者组 失败,后两局都胜,方可得冠军;若在胜者组 胜利,
后一局(与败者组胜者比赛)胜,方可得冠军,此时获得冠军的概率为 ;
当 进入败者组,后三局都胜,方可得冠军,此时 获得冠军的概率为 ,
因此 获得冠军的概率为 ,
,
由 ,得 , ,若 为强队,则 ,此时 ,
即 ,因此 , 获得冠军的概率更大,