数学答案_2024-2025高二（7-7月题库）_2024年12月试卷_1220安徽省“江南十校”2024年高二年级12月份阶段联考_安徽省江南十校2024-2025学年高二上学期12月联考数学试卷

2024-2025 高二数学试题 参考答案及评分细则 一、选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目 要求的. 题号 1 2 3 4 5 6 7 8 答案 C B A D B C B C 1．【答案】C     【解析】由题意ab，得1，即ab0,4,4，故选C. 2．【答案】B 【解析】m0,n0且mn时方程mx2 ny2 1表示的曲线是椭圆，故选B 3．【答案】A 【分析】根据点与直线的位置关系即可求解. 【详解】因为P(3,4)是直线axby20和a xb y20的公共点， 1 1 2 2 所以3a 4b 20，且3a 4b 20，所以两点Aa,b和Ba ,b 都在同一条直线3x4y20上， 1 1 2 2 1 1 2 2 故直线AB方程是3x4y20，故选A. 4．【答案】D      【解析】易知PD BQ ac b，设CQ 中点为E，则  2 1    1     1     BG  BE  BQBC  BQPCPB  a 2b 2c ， 3 3 3 3     1     1 1 2 所以PG  PBBG b a2b2c  a b c，故选D 3 3 3 3 5．【答案】B    2 【解析】由题意直线l的方向向量m 2,1,1 ,PQ  3,4,5，则 PQ 32 42 52 50，    PQm 64515， m  6，所以点Q2,4,6到直线l的距离为   2  2  PQm   15  2 5 2 d  PQ     50    ，故选B.  m   6  2   6．【答案】C 【解析】圆C的方程为，x2  y1 2 2，圆心为0,1，半径为 2，过点2,1作圆C的切线，设其 学科网（北京）股份有限公司k012k 1 方程为 y1 kx2，即kx y2k 10，则  2 ，解得k  1，则结合图像 k2 1 2ab5 b1 知 2 的取值范围为  1,3  ， 故选C. 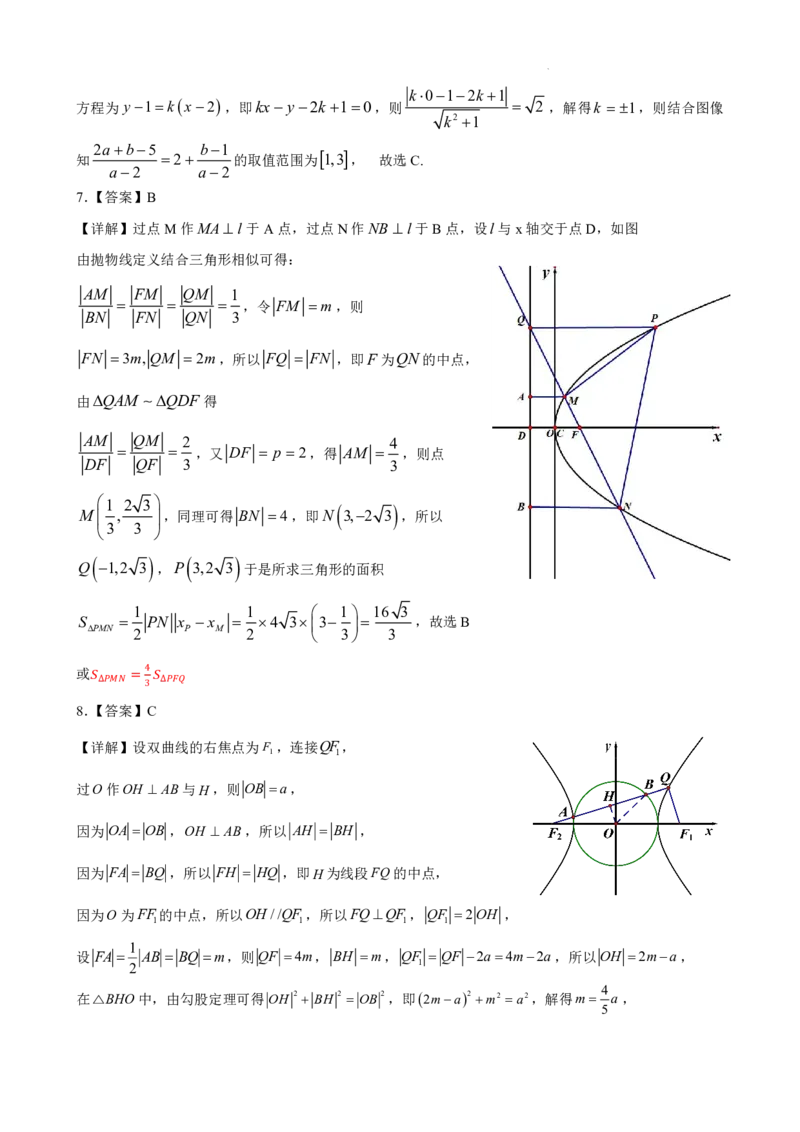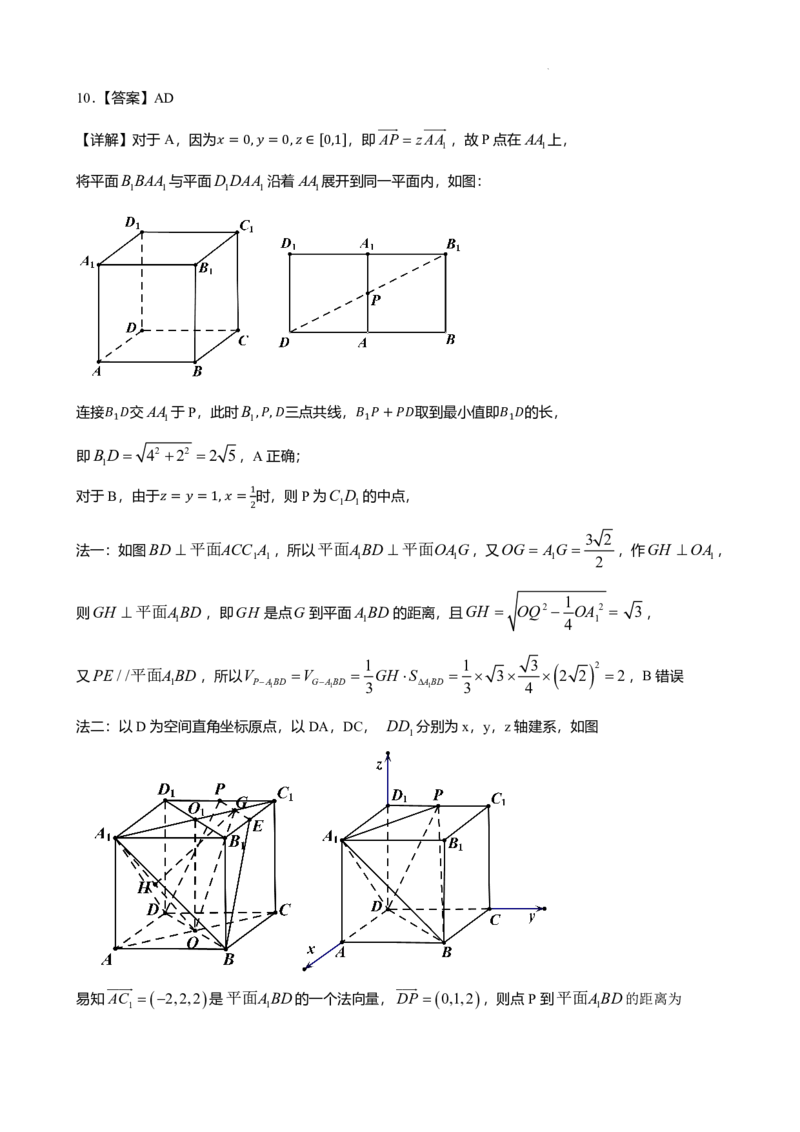a2 a2 7．【答案】B 【详解】过点M作MAl 于A点，过点N作NB l于B点，设l与x轴交于点D，如图 由抛物线定义结合三角形相似可得： AM FM QM 1    ，令 FM  m，则 BN FN QN 3 FN 3m,QM  2m，所以 FQ  FN ，即F为QN的中点， 由QAM QDF 得 AM QM 2 4   ，又 DF  p  2，得 AM  ，则点 DF QF 3 3 1 2 3   M  , ，同理可得 BN  4，即N 3,2 3 ，所以 3 3      Q 1,2 3 ，P 3,2 3 于是所求三角形的面积 1 1  1 16 3 S  PN x x  4 3 3   ，故选B PMN 2 P M 2  3 3 或 4 8． 【 ∆ 答 案 = 】3 C ∆ 【详解】设双曲线的右焦点为F ，连接QF， 1 1 过O 作OH  AB与H，则 OB a， 因为 OA  OB ，OH  AB，所以 AH  BH ， 因为 FA  BQ ，所以 FH  HQ ，即H为线段FQ的中点， 因为O为FF的中点，所以OH//QF ，所以FQQF ， QF 2OH ， 1 1 1 1 1 设 FA  AB  BQ m，则QF 4m， BH m，QF  QF 2a4m2a，所以OH 2ma， 2 1 4 在△BHO中，由勾股定理可得OH 2 BH 2  OB 2，即2ma2 m2 a2，解得m a， 5 学科网（北京）股份有限公司3 8 所以OH 2ma  a， FH 2m a，在△FHO中，由勾股定理得 OH 2  FH 2  OF 2， 5 5 2 2 3  8  73 c 73 即  a  a c2，解得c a ，所以e  . 5  5  5 a 5 故选：C. 二、多项选择题：本大题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求. 全部选对的得6分，部分选对的得部分分，有选错的得0分. 题号 9 10 11 答案 BCD AD ABD 9．【答案】BCD x y 【详解】对于A：设过点P3,2与坐标轴的正半轴相交的直线l方程为：  1，则 a b 3 2 3 2 1  1 2   ab 24 ，即直线l与坐标轴围成三角形的面积的最小值为S  ab12， a b a b 2 所以与坐标轴的正半轴围成三角形面积为16的直线有2条，另外过点P3,2与x轴正（负）半轴，与y 轴负（正）半轴围成三角形面积S0,，即面积为16的直线各有1条，故共有4条；A错误 对于B：因为 AB 5，以A，B为圆心，分别以2,3为半径作圆，则圆A与圆B相外切，它们的3条公 切线即为满足条件的直线，所以B正确； 对于C：因为 y2 4x，当x 2时， y 2 2 3，所以点Q在抛物线的外部，所以C正确， x2 y2 2b2 对于D：过双曲线  1的右焦点作垂直实轴的直线 l ，被双曲线右支截得的弦（通径）长为 5， 4 5 a 又双曲线的实轴长2a  45，所以结合对称性可知，被双曲线左右两支截得的线段长为5的直线有2条， 共有3条，所以D正确； 故选BCD 学科网（北京）股份有限公司10．【答案】AD   【详解】对于A，因为 ，即AP  zAA ，故P点在AA上， 1 1 = 0, =0, ∈ 0,1 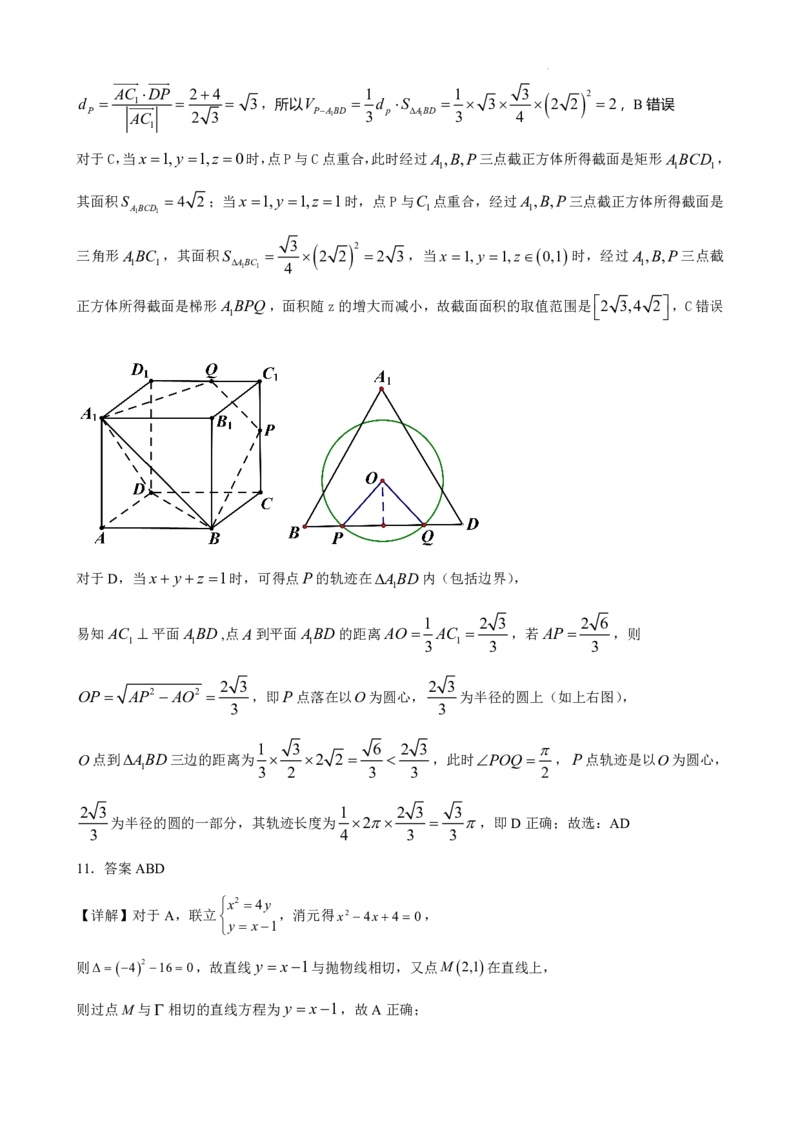将平面BBAA 与平面D DAA 沿着AA展开到同一平面内，如图： 1 1 1 1 1 连接 交AA 于P，此时B 三点共线， 取到最小值即 的长， 1 1 1 , , 1 + 1 即BD  42 22 2 5，A正确； 1 对于B，由于 时，则P为C D 的中点， 1 1 1 = =1, =2 3 2 法一：如图BD 平面ACC A ，所以平面ABD 平面OAG，又OG  AG  ，作GH OA ， 1 1 1 1 1 2 1 1 则GH 平面ABD，即GH 是点G 到平面ABD的距离，且GH  OQ2 OA2  3， 1 1 4 1 1 1 3  2 又PE //平面ABD ，所以V V  GH S   3  2 2 2，B错误 1 PA 1 BD GA 1 BD 3 A 1 BD 3 4 法二：以D为空间直角坐标原点，以DA，DC， DD 分别为x，y，z轴建系，如图 1   易知AC 2,2,2是平面ABD的一个法向量，DP  0,1,2，则点P到平面ABD的距离为 1 1 1 学科网（北京）股份有限公司  AC DP 24 1 1 3  2 d  1   3，所以V  d S   3  2 2 2，B错误 P AC 2 3 PA 1 BD 3 p A 1 BD 3 4 1 对于C，当x 1,y 1,z 0时，点P与C点重合，此时经过A,B,P三点截正方体所得截面是矩形ABCD ， 1 1 1 其面积S  4 2；当x 1,y 1,z 1时，点P与C 点重合，经过A,B,P三点截正方体所得截面是 A1BCD1 1 1 3  2 三角形 ABC ，其面积S   2 2 2 3，当x 1,y 1,z0,1时，经过A,B,P三点截 1 1 A 1 BC 1 4 1 正方体所得截面是梯形ABPQ，面积随z的增大而减小，故截面面积的取值范围是2 3,4 2，C错误 1   对于D，当x yz 1时，可得点P的轨迹在ABD内（包括边界）， 1 1 2 3 2 6 易知AC 平面ABD,点A到平面ABD的距离AO  AC  ，若AP ，则 1 1 1 3 1 3 3 2 3 2 3 OP  AP2  AO2  ，即P点落在以O为圆心， 为半径的圆上（如上右图）， 3 3 1 3 6 2 3  O点到ABD三边的距离为  2 2   ，此时POQ  ，P点轨迹是以O为圆心， 1 3 2 3 3 2 2 3 1 2 3 3 为半径的圆的一部分，其轨迹长度为 2  ，即D正确；故选：AD 3 4 3 3 11．答案ABD x2 4y 【详解】对于A，联立 ，消元得x2 4x40， y  x1 则Δ 42 160，故直线 y  x1与抛物线相切，又点M2,1在直线上， 则过点M与相切的直线方程为 y  x1，故A正确； 学科网（北京）股份有限公司对于B，由题意，设A(x ,y ),B(x ,y )，则 0 0 0 0 y 1 y 1  1 1  4 k k  0  0 y 1   y 1 ， MA MB x 2 x 2 0 x 2 x 2 0 x 24 0 0 0 0 0 4 4 注意到x 2 4y ,，于是k k y 1 y 1 1为定值，B选项正确. 0 0 MA MB 0 x 24 0 4y 4 0 0 对于C，依题知，直线AB的斜率存在且不为零，设直线AB的方程为mx2ny11， x2 4y x224x24 y1 联立 ，得4ny12 4m4nx2 y1 14m x2 2 0， mx2ny11 即4n   x y   2 1   2 4m4n   x y   2 1   14m0，设Ax 1 ,y 1 ,Bx 2 ,y 2 ，则 y 1 y 1 k  1 ,k  2 是方程4nk24m4nk14m0的两个根，由韦达定理知 1 x 2 2 x 2 1 2 14m 1  1 kk  1解得nm ，此时直线AB的方程为mx2m  y11即 1 2 4n 4  4 y 3 mxy1  0，恒过定点2,3，故C错误； 4 4 x2 x 2 x2 对于D， 设A(x, 1 ),B(x , 2 )，以A为切点的切线l 方程为 y 1 k  xx ， 1 4 2 4 PA 4 1  x2 y 1 kxx  则  4 1  x2 4kx4kx  x2  0 ，令 16k2 4  4kx x2   4k 2x 2 0得 1 1 1 1 1  x2 4y x x x2 k  1 ，所以切线l 方程为 y  1 x 1 ，同理可得以M为切点的切线l 方程为： y  x1，以B PA PQ 2 2 4 x x 2 为 切 点 的 切 线 l 方 程 为 y  2 x 2 ， 联 立 l 与 l 的 方 程 可 得 BQ PQ PA 2 4  x x2 y  1 x 1 x x2 x x x  2 4  1 x 1  x1 x  1 1，即点P的横坐标为 1 1，由题意x  1 1，则 2 4 2 2 2 2  y  x1 x2 x x 2 1 1 切线BQ的斜率k  2  1 ，又直线AM的斜率 4 x 2 ，即k k ， BQ 2 4 k   1 AM BQ AM x 2 4 1 所以AM //BQ，即D正确，故选ABD 学科网（北京）股份有限公司三、填空题：本大题共3小题，每小题5分，共15分。把答案填在题中的横线上。 5 1 12. （0， ） 13. 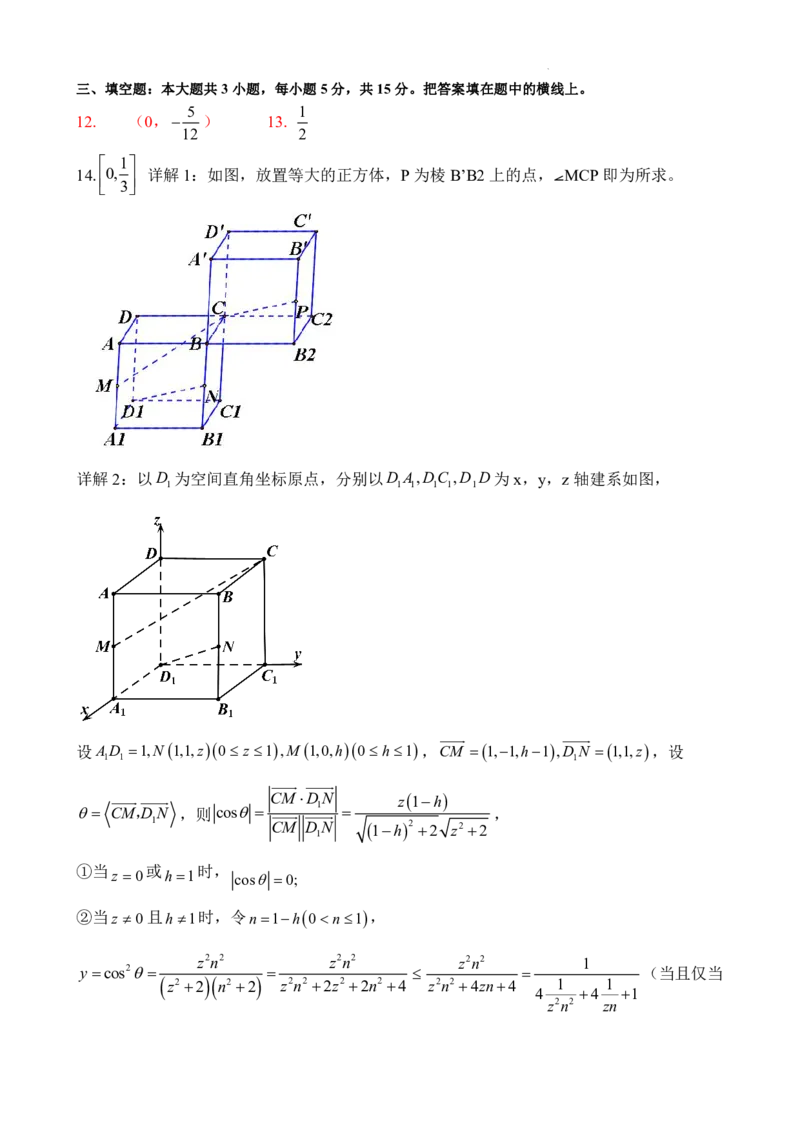12 2  1 14. 0,  详解1：如图，放置等大的正方体，P为棱B’B2 上的点， MCP即为所求。  3 ⦟ 详解2：以D 为空间直角坐标原点，分别以D A,DC ,D D为x，y，z轴建系如图， 1 1 1 1 1 1   设AD 1,N 1,1,z0 z 1,M 1,0,h0 h 1，CM 1,1,h1,D N 1,1,z，设 1 1 1    CM DN z1h  CM，D N ，则 cos    1   ， 1 CM DN 1h2 2 z2 2 1 ①当 或 时， z  0 h 1 cos 0; ②当z  0且h 1时，令n 1h0 n1， z2n2 z2n2 z2n2 1 ycos2    （当且仅当  z2 2  n2 2  z2n2 2z2 2n2 4 z2n2 4zn4 1 1 4 4 1 z2n2 zn 学科网（北京）股份有限公司1 1 n z取等号），令t  ,t 1，函数4t24t1在 1,为增函数，故9.故cos2 ， zn 9 1 所以0 cos  . 3 1 综上：0 cos  . 3 四、解答题：本题共 5小题，共 77分.解答应写出文字说明、证明过程或演算步骤. 62 1 15.解：（1）易求A,B中点坐标为T  5,4 ，k  2，故AB中垂线为y4  x5 ， AB 46 2 1 3 即 y  x ，与 y 2x联立解得圆心C点坐标为 1,2 ， 2 2 圆的半径r   16 2  22 2 5，故圆C:  x1 2  y2 2 25…………………5分 (2)设P,Q中点坐标为N ，CN  PQ，故N 点在CD为直径的圆上，设CD中点M ，以CD为 2 2  5  3 5 直 径 的 圆 M 的 方 程 ：  x4  x1  y1  y2 0 ， 即 x   y   ， 故  2  2 2    OPOQ  2ON  34 10 ， 当 且 仅 当 O,M,N 三 点 共 线 时 取 等 号 ， 故   OPOQ  34 10..………………………………13分 max    另解：①当直线PQ的斜率不存在时，PQ中点坐标T  4,2 ， OPOQ  2OT  4 5 ； ②当直线PQ的斜率存在时，设直线PQ：y1k  x4 代入 x1 2  y2 2 25整理得：     k2 1 x2  8k2 2k 2 x4k2 8k 230 8k2 2k 2 4k2 6k 2 设P  x ,y  ,Q  x ,y ，则x x  ，y  y  1 1 2 2 1 2 k2 1 1 2 k2 1  2  2     8k2 2k 2  4k2 6k 2 8 10k4 2k3 11k2 2k 1 2 OPOQ    2  2 k2 1 k2 1    8 k2 1 10k2 2k 1  2k9    810  ，因为求 OPOQ 的最大值，可令t 2k90，  k2 1 2  k2 1 t9 k  代入上式可得： 2 学科网（北京）股份有限公司        2  t   4t   4  OPOQ 8 10 810  810      t9  2 1    t2 18t85  t18 85   t    2    4   2 859 810  444 85  34 10 ，当且仅当t  85 ，即k  时取等号.  2 8518 2   易求4 5  34 10 ，故 OPOQ  34 10. 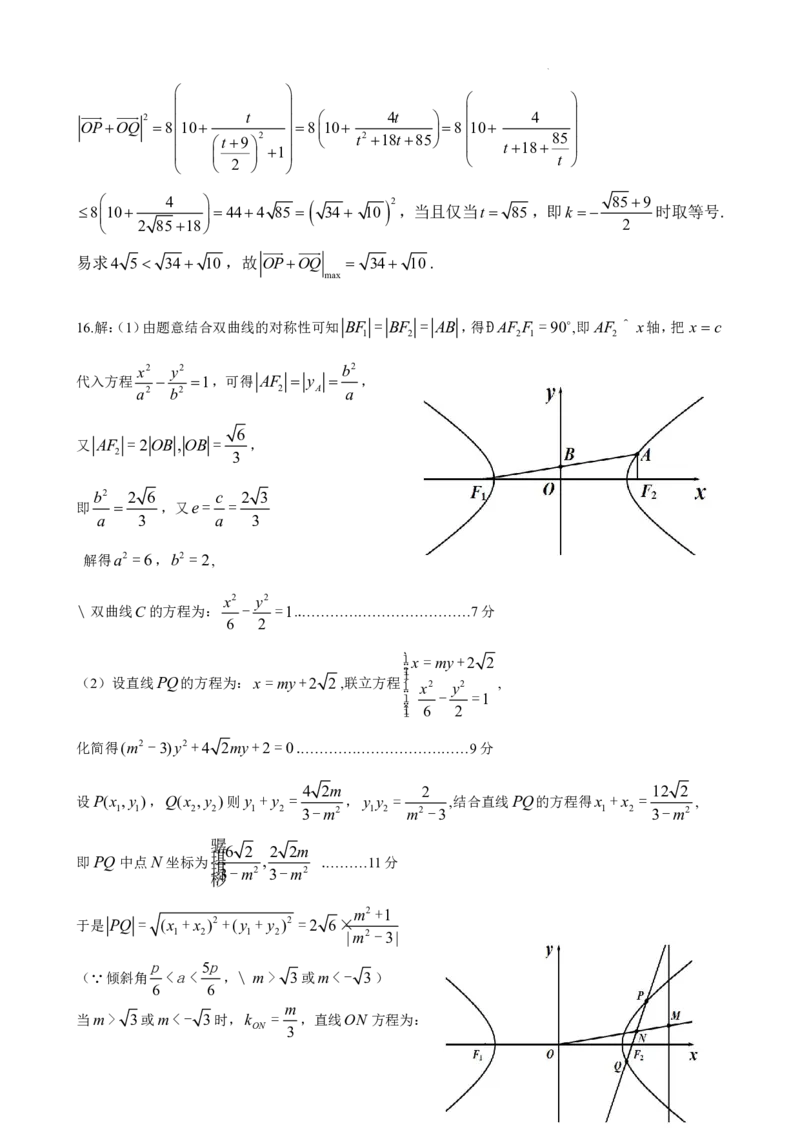max 16.解：（1）由题意结合双曲线的对称性可知 BF = BF = AB ，得ÐAF F =90,即AF ^ x轴，把 x c 1 2 2 1 2 x2 y2 b2 代入方程  1，可得 AF  y  ， a2 b2 2 A a 6 又 AF =2OB ,OB = ， 2 3 b2 2 6 c 2 3 即  ，又e= = a 3 a 3 解得a2 =6，b2 =2, x2 y2 \ 双曲线C的方程为： - =1..………………………………7分 6 2 ì x=my+2 2 ï ï （2）设直线PQ的方程为：x= my+2 2,联立方程í x2 y2 , ï - =1 ïî 6 2 化简得(m2 -3)y2 +4 2my+2=0.………………………………9分 4 2m 2 12 2 设P(x ,y )，Q(x ,y )则 y + y = ， y y = ,结合直线PQ的方程得x +x = , 1 1 2 2 1 2 3-m2 1 2 m2 -3 1 2 3-m2 骣 琪6 2 2 2m 即PQ 中点N 坐标为 琪 , .………11分 桫3-m2 3-m2 m2 +1 于是 PQ = (x +x )2 +(y + y )2 =2 6× 1 2 1 2 |m2 -3| p 5p （倾斜角 3或m<- 3） 6 6 m 当m> 3或m<- 3时，k = ，直线ON 方程为： ON 3 学科网（北京）股份有限公司y = m 3 x，令x = 3 2 2 得M 骣 琪 琪 桫 3 2 2 , 2 2 m ，此时 MF 2 2 =ç 骣 琪 桫 2 2- 2 3 2÷ 2 + 骣 琪 琪 桫2 2 m 2 = m2 2 +1 ,于是 PQ 2 48(m2+1) PQ2 48(4-t) 4 1 1 4 = ，令t =3-m2Î ( 0,3 ]，则 = = 48( - )= 48 ( -1)³ 0 ， MF 2 (3-m2)2 MF 2 t2 t2 t t t 2 2 骣 1 1 PQ2 1 4 16 PQ 4 由 ³ 知，琪 琪 =48创 （ -1）= ，故 的最小值为 3..……………15分 t 3 桫MF 2 3 3 3 MF 3 2 min 2 17．【解析】（1）取F为PD三等分点，且PD3DF，过F作FK∥CD， 2 则FK  CD AE，所以AEKF为平行四边形，所以AF∥EK， 3 又AF 面PEC ，EK 面PEC， 所以AF //平面PEC，证毕； …………………………………………………………6分 （2）由题意平面PAD 底面ABCD,平面PAD底面ABCD  AD CD  AD，所以CD面PAD， 所以直线CF 与平面PAD所成角的平面角为CFD， CD 3 在RtCDF 中，由tanCFD   ，得DF  4． ……………………………………………8分 FD 2 设AD中点为O，设BC中点为Q，分别以OA,OQ,OP为x，y，z轴建立空间直角坐标系，         则A3,0,0,B3,6,0C 3,6,0,F 1,0,2 3 ，AF  4,0,2 3 ,CF  2,6,2 3 ，……10分  设平面AFC的一个法向量为mx,y,z，   mAF 4x2 3z0    由   ，取x 3，可得m 3, 3,2 ， …………………12分 mCF 2x6y2 3z0    易求平面 ABC法向量n0,0,1，设平面ABC与平面AFC夹角为 0, ，则  2 学科网（北京）股份有限公司    mn 2 10 cos cos m,n      ， …………………14分 m  n 334 5 10 故平面ABC与平面AFC夹角的余弦值为 ． …………………15分 5 （其他做法，请参照给分）   c 1 e   a 2   18.解：（1）依题意可得： a2 b2 c2 ，解得：a 2,c1,b 3  9  1   4 1 a2 b2 x2 y2 故椭圆E :  1………………………………………………………4分 1 4 3 （2）若AB斜率不存在或为0，有对称性知：AP BQ 若AB斜率存在且不为0，设AB中点为Tx ,y ，Ax ,y ,Bx ,y ，则 0 0 1 1 2 2 x2 y2 x2 y2 1  1 1① 2  2 1②①②得： 16 12 16 12  x x  x x   y  y  y  y  y y y 3 3 1 2 1 2  1 2 1 2 0， 1 2  0  即k k  ， …………6分 16 12 x x x 4 AB OT 4 1 2 0 3 3 设PQ中点为T'，同理可得：k k  ，即k k  ，故T 与T'重合. PQ OT' 4 AB OT' 4 PT QT,AT  BT，AP AT PT  BT QT BQ，得证.…………10分 （3）由（2）知：APBQ，同理PC DH，AQAP+PQ=BQ+PQ=PB，同理CH  DP， 3 即证： PA  PB  PC  PD ，设直线AB: y k  x1  2 代入 x2  y2 1整理得： 34k2  x2 8k   3 k  x4   3 k   2 480…………12分 16 12 2  2  2 3  4 k 48 12k8k2 2  设Ax ,y ,Bx ,y ，则x x  ，x x  3 3 4 4 3 4 34k2 3 4 34k2 学科网（北京）股份有限公司PA PB  1k2 1x 1k2 1x =  1k2  1 x x x x   1k2  36 ………15分 3 4 3 4 3 4 34k2 因为直线l ,l 的倾斜角互补，则l 的斜率为k ，同理可得 1 2 2   36 PC  PD  1k 2 = PA  PB ，得证.………17分 34 k 2 x 1tcos  x2 y2 另解：设直线AB: 3 代入  1整理得： y  tsin 16 12  2  14sin2  t2  24cos48sin t1320…………12分 132 132 t t  ， PA  PB  t t  ， 1 2 14sin2 1 2 14sin2 132 132 用代得： PD  PC   ，…………15分 14sin2 14sin2 所以 PA  PB  PC  PD ，得证..………17分         19.解：（1）ACCB，OCOAOBOC ，     1    1OC OAOB，故OC  OA OB.………4分 1 1  AC （2）设 A,B;C ,即 ，因为A,B,C是共线的三个不同点，故0. CB        BA 1 1 所以 AC   ABAC  1AC AB  BA  1 ，即 B,C:A 1 . ， ， AC   1 同理 B,A;D  ，所以B,C;AB,A;D1..………9分  （3）设A,B;D,B,C;E,C,A;F，因为A,B和D三点共线，A,B;D，参照  1    （1）证明可得：MD  MA MB① 1 1  x  又因为M,C,D三点共线，所以存在xR，使得MD MC，代入①式可得： 1     MAMBxMC 0② 同理，利用B,C;E,C,A;F，可以找到实数 y和z ，使得     yMAMBMC 0③ 学科网（北京）股份有限公司    MAzMBMC 0④      联立②③消去MB，联立②④消去MA，可得：1yMAxMC 0，       zMBx1MC 0，又因为MA，MB和MC 中任意两个向量互不共线，故有 1 1 1 1y  xz  x10，由此推出x ,y  ,z  ，    1，即A,B;DB,C;EC,A;F1.得证..………17分 学科网（北京）股份有限公司