数学答案_2024-2025高二（7-7月题库）_2024年11月试卷_1123四川省南充市嘉陵一中2024-2025学年高二上学期第二次月考（11月）

高二数学期中答案学生版
参考答案：
题号 1 2 3 4 5 6 7 8 9 10
答案 B B B C C C C C BC ABD
题号 11
答案 ABD
12．2
13．,1 

 1,
2 4
14． 6  , 
5 5
15．（1）2xy50（2）直线l 的方程为：x2y40或x2y40
2
【详解】试题分析：（1）由直线l 与l垂直，可设直线l 的方程为：2xyc0，将点1,3 代入方程解得c5，
1 1
从而可得直线l 的方程；(2)由直线l 与l平行，可设直线l 的方程x2yc0，由直线l 与两坐标轴围成的三角形
1 2 2 2
的面积为4，解得c4可得直线l 的方程.
2
试题解析：（1）设直线l 的方程为：2xyc0
1
直线l 过点（1，-3），213c0
1
解得c5
直线l 的方程为：2xy50．
1
(2)设直线l 的方程为：x2yc0
2
c
令 ，得y ；令y0，得xc
2
毀1ᷯ c
则s  c 4，得c4
2 2
直线l 的方程为：x2y40或x2y40．
2
16．(1)30
(2)众数为55；第80百分位数为66
8
(3)
15
【分析】（1）先根据频率分布直方图求出频率，再根据频数的计算方法可得答案；
（2）最高矩形中点横坐标即为众数；根据百分位数的定义可求得样本的第80百分位数；
（3）计算抽取的人中，位于[20,30)的有2人，记为a,b，数学成绩位于[30,40)的有4人，记为A,B,C,D，列举出
所有的基本事件，并确定所求事件所包含的基本事件，利用古典概型的概率公式即可求解.
答案第1页，共6页【详解】（1）由频率分布直方图知，年龄在区间[40,70)上的频率为：0.0200.0300.025100.75
所以40名读书者中年龄分布在区间上的人数为：400.7530
（2）由频率分布直方图可知，40名读书者年龄的众数约为55；
年龄在区间[20,60)上的频率为：0.0050.0100.0200.030100.650.8
年龄在区间[20,70)上的频率为：0.0050.0100.0200.0300.025100.90.8，
故第80百分位数位于 之间，设为x，
所以0.65x600.0  2 ᷯ 5 hᷯ 0.8，解得x66，
所以这40名读书者年龄的第80百分位数约为66.
（3）由频率分布直方图知：年龄在区间[20,30)上的读书者有400.005102人，
分别记为a,b，年龄在区间[30,40)上的读书者有400.010104人，分别记为A,B,C,D，
从上述6人中选出2人，则有
a,b,a,A,a,B,a,C,a,D,b,A,b,B,b,C,b,D,A,B,A,C,A,DB,C,B,D,C,D，共15种情况；
其中恰有1人在[30,40)的情况有a,A,a,B,a,C,a,D,b,A,b,B,b,C,b,D，共8种情况；
8
所以恰有1人在[30,40)的概率为 .
15
17．(1)(x3)2(y4)2 4
(2)xy10或7xy70
【分析】（1）设点M(x,y),A(x,y )，根据题意得到A(2x6,2y8)，代入圆x2y2 16，即可求解；
1 1
2k4
（2）根据题意，设直线l:yk(x1)，求得圆心M(3,4)到直线l的距离为d  ，得到
k21
1
S  d2 4d2 d 4d2 ，结合基本不等式，求得最小值，进而求得直线的方程.
CPQ 2
【详解】（1）解：设点M(x,y),A(x,y )，由点B的坐标为6,8，且M 是线段AB的中点，
1 1
 x 6
x 1

 2
则 ，可得x 2x6,y 2y8，即A(2x6,2y8)，
 y y 1 8 1 1
 2
因为点A在圆x2y2 16上运动，所以点A点坐标满足圆的方程x2y2 16，
即(2x6)2(2y8)2 16 ，整理得(x3)2(y4)2 4 ，
所以点M 的轨迹方程为(x3)2(y4)2 4 .
答案第2页，共6页（2）解：过点定点 的直线l与曲线C交于P,Q两点，则直线l的斜率一定存在且不为0，
设直线l:yk(x1)，hᷯ即kx  y  k  0，
2k4
则圆心M(3,4)到直线l的距离为d  ，
k21
1 d2(4d2)
又因为S  d2 4d2 d 4d2  2，
CPQ 2 2
当且仅当d  4d2 时，即d  2时，等号成立，
2k4
所以d  2时，S
△CPQ
取得最大值2，此时d   2，解得k 1或k 7，
k21
所以S 取得最大值2，此时直线l的方程为xy10或7xy70.
△CPQ
18【分析】（1）根据线面垂直的性质定理，结合线面垂直的判定定理进行证明即可；
（2）根据线面的垂直关系，建立空间直角坐标系，利用空间向量平面间夹角公式进行求解即可；
（3）利用空间向量线面角夹角公式进行求解即可.
【详解】（1）因为PD平面ABCD,AB 平面ABCD，
所以PD AB，
又因为AB∥CD,ADC 90，
所以ADAB，而ADPD D,AD,PD 平面PAD，
所以AB平面PAD；
（2）因为PD平面ABCD,AD,CD平面ABCD，
所以PDCD,PD AD，而CD AD，
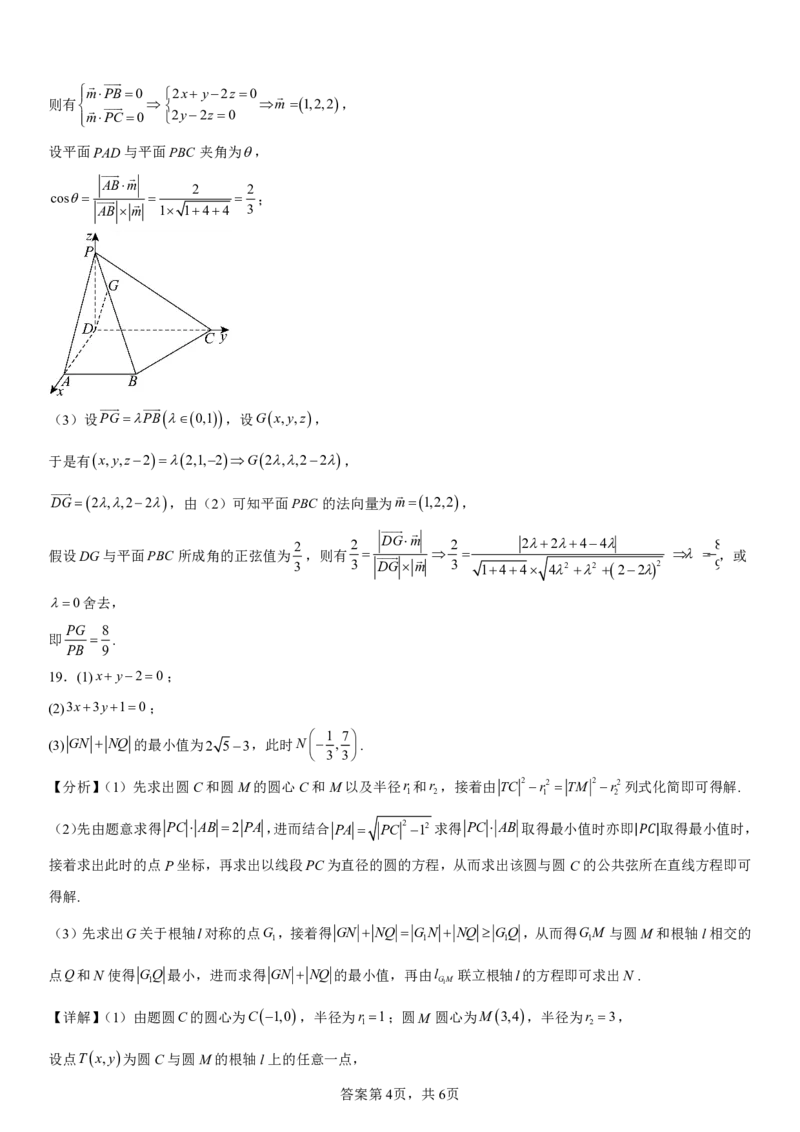
于是建立如图所示的空间直角坐标系，
D0,0,0,P0,0,2,A2,0,0,B2,1,0,C0,2,0，
由（1）可知：AB平面PAD，

所以平面PAD的法向量为AB0,1,0，
 
设平面PBC 的法向量为 ，PB2,1,2,PC  0,2,2，
毀 hh
答案第3页，共6页 
 mPB0 2x y2z0 
则有 m    P  C  0    2y2z0 m 1,2,2，
设平面PAD与平面PBC 夹角为，
 
ABm
2 2
cos     ；
AB  m 1 144 3
 
（3）设PGPB 0,1 ，设Gx,y,z，
于是有x,y,z22,1,2G2,,22，
 
DG 2,,22，由（2）可知平面PBC 的法向量为m1,2,2，
 
2 2 DGm 2 2244 8
假设DG与平面PBC 所成角的正弦值为 ，则有        ，或
3 3 DG m 3 144 42 2 222 9
0舍去，
PG 8
即  .
PB 9
19．(1)xy20；
(2)3x3y10；
 1 7
(3)GN  NQ 的最小值为2 53，此时N , .
 3 3
【分析】（1）先求出圆C和圆M的圆心C和M以及半径r和r ，接着由TC 2r2  TM 2r2列式化简即可得解.
1 2 1 2
（2）先由题意求得 PC  AB 2 PA ，进而结合 PA  PC 212 求得 PC  AB 取得最小值时亦即 取得最小值时，

接着求出此时的点P坐标，再求出以线段PC为直径的圆的方程，从而求出该圆与圆C的公共弦所在直线方程即可
得解.
（3）先求出G关于根轴l对称的点G ，接着得GN  NQ  GN  NQ  GQ ，从而得GM 与圆M和根轴l相交的
1 1 1 1
点Q和N使得 GQ 最小，进而求得 GN  NQ 的最小值，再由l 联立根轴l的方程即可求出N.
1 G1M
【详解】（1）由题圆C的圆心为C1,0，半径为r 1；圆M 圆心为M3,4，半径为r 3，
1 2
设点Tx,y为圆C与圆M的根轴l上的任意一点，
答案第4页，共6页则由题可得TC 2r2  TM 2r2，即x12 y212 x32y4232，
1 2
整理得xy20，即圆C与圆M的根轴l为直线xy20.
（2）由题意可知PC  AB且 PB  PA ，PACA,PBCB，
设PC与AB相交于点H，
则S  1 PC HA  1 PC HB  1 PC  HA  HB  1 PC AB ，
四边形PACB
2 2 2 2
1 1 1 1
又S  PA CA  PB CB  PA  PB  PA，
四边形PACB
2 2 2 2
所以 PC  AB 2 PA ，所以 PC  AB 取得最小值时即为 PA 取得最小值时，
又 PA  PC 212 ，所以 PC  AB 取得最小值时亦即 取得最小值时，

102 3 2
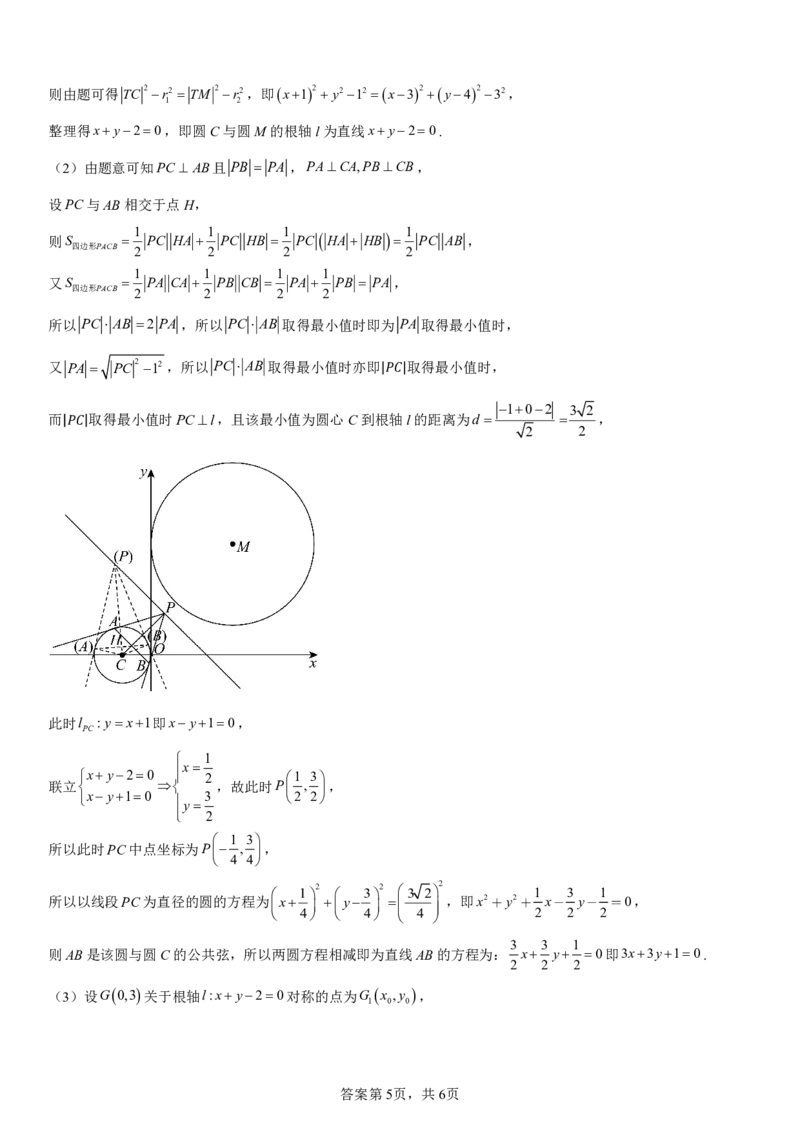
而 取得最小值时PCl，且该最小值为圆心C到根轴l的距离为d   ，
2 2

此时l :yx1即xy10，
PC
 1
x
xy20   2 1 3
联立  ，故此时P , ，
xy10  y 3 2 2
 2
 1 3
所以此时PC中点坐标为P , ，
 4 4
 1 2  3 2  3 2 2 1 3 1
所以以线段PC为直径的圆的方程为 x  y      ，即x2+y2+ x- y- =0，
 4  4  4  2 2 2
3 3 1
则AB是该圆与圆C的公共弦，所以两圆方程相减即为直线AB的方程为： x y 0即3x3y10.
2 2 2
（3）设G0,3关于根轴l:x y20对称的点为G x ,y ，
1 0 0
答案第5页，共6页y 3
0 1
 x 0 x 1
则 0   0 ，故G 1,2，
x
0
0

y
0
3
2 0
y
0
2 1

2 2
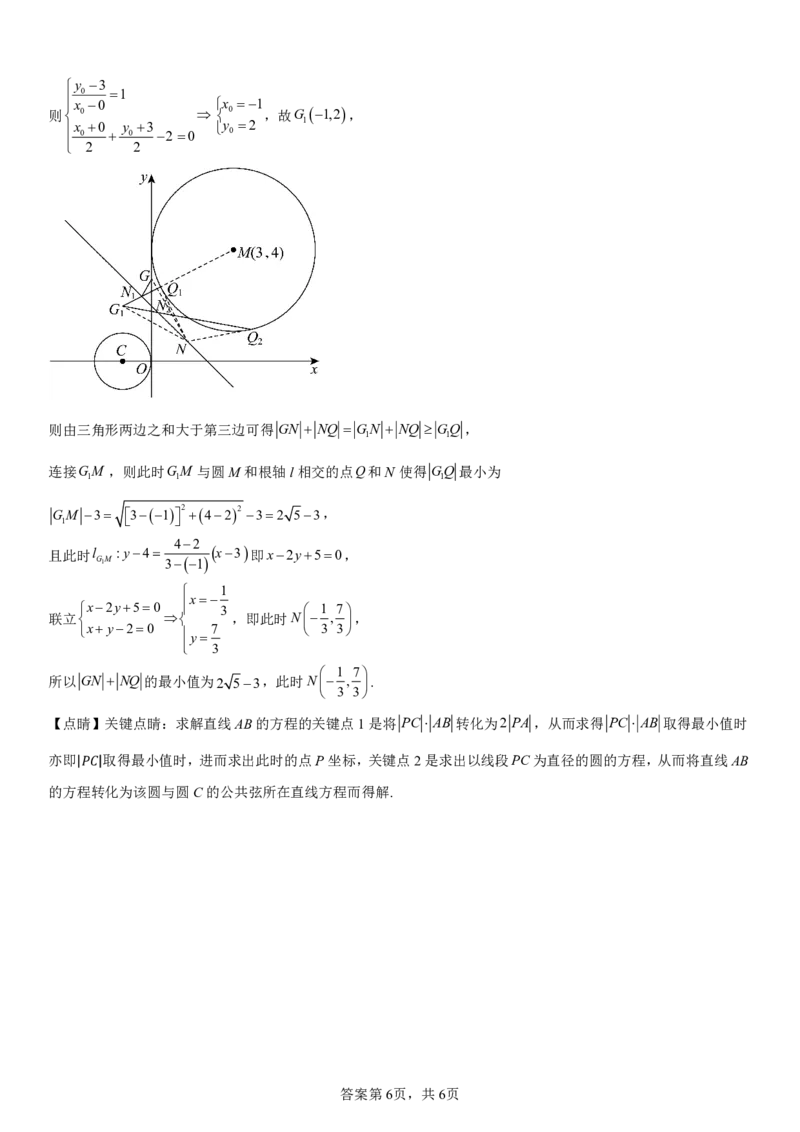
则由三角形两边之和大于第三边可得 GN  NQ  GN  NQ  GQ ，
1 1
连接GM ，则此时GM 与圆M和根轴l相交的点Q和N 使得 GQ 最小为
1 1 1
G 1 M 3  31  2 422 32 53，
42
且此时l :y4 x3 即x2y50，
G1M 31
 1
x
x2y50   3  1 7
联立  ，即此时N , ，
xy20  y 7  3 3
 3
 1 7
所以 GN  NQ 的最小值为2 53，此时N , .
 3 3
【点睛】关键点睛：求解直线AB的方程的关键点1是将 PC  AB 转化为2 PA ，从而求得 PC  AB 取得最小值时
亦即 取得最小值时，进而求出此时的点P坐标，关键点2是求出以线段PC为直径的圆的方程，从而将直线AB
的方程转化为该圆与圆C的公共弦所在直线方程而得解.
答案第6页，共6页