数学答案_2024-2025高二（7-7月题库）_2024年12月试卷_1205浙江省六校联盟2024-2025学年高二期中联考_浙江省六校联盟2024-2025学年高二上学期期中联考数学试题

保密★考试结束前
六校联盟2024学年第一学期期中联考
(2024.11)
高二数学参考答案及评分标准
一、选择题(本题共8小题，每小题5分，共40分。每小题列出的四个备选项中只有一个是符合题目要求
的，不选、多选、错选均不得分)
题号 1 2 3 4 5 6 7 8
答案 B D D C C D B A
二、选择题(本题共3小题，每小题6分，共18分。每小题列出的四个备选项中至少有一个是符合题目要
求的。全部选对的得6分，部分选对得部分分，有选错的得0分)
题号 9 10 11
答案 AC ACD ABC
三、填空题(本题共3小题，每小题5分，共15分)
12. 14 (5分)
13. 24 (5分)
14. x2y2 3 (5分)
四、解答题(本题共5小题；其中第15小题13分，第16小题15分，第17小题15分，第18小题17分，第19
小题17分；共77分)
15.(13分)
(1)连ON ，MN ONOM …………(2分)
1 1 2 1 1 2
OM  OA a，ON  OC OB b c …………(3分)
2 2 3 3 3 3
1 1 2
MN  a b c …………(1分)
2 3 3
1 1 2 2 1 1 2 2
(2) MN  a b c，所以 MN   a b c …………(2分)
2 3 3 2 3 3
1 2 1 2 4 2 1 2 4
 a  b  c  ab ac bc …………(1分)
4 9 9 3 3 9
因为是正四面体，OA4，
2 2 2
所以a b c 16，abacbc8 …………(3分)
2 116 40 76 2 19
MN    .所以 MN  …………(1分)
9 9 9 3
16.(15分)
(1)设Px,y，因为 PB 2 PA
所以 x22y2 2 x12y2 …………(2分)
平方化解可得x24xy2 0，即x22y2 4 …………(4分)
六校联盟期中联考【高二数学】答案及评分标准(第1页,共5页)
{#{QQABCYaEoggAAAAAAAgCAwFyCEKQkgACCSgOAFAEoAAASRNABAA=}#}(2)已知直线l:ykx1与圆C 交于P，Q两点，设Px,y ,Qx ,y 
1 1 1 2 2
ykx1

联立 ，得(1k2)x22k4x10 …………(2分)
 x22 y2 4

Δ4k22 4  k21  0

 2k4  3 
所以

x
1
x
2

1k2
，得k


4
,

…………(2分)
 1
  x 1 x 2  1k2
OPOQx x y y   1k2 x x kx x 1
2k24k
23 …………(3分)
1 2 1 2 1 2 1 2 1k2
1 3 1
解得k  或-1，因为k  ，所以k  …………(2分)
3 4 3
17.(15分)
(1)在四棱锥中P-ABCD，平面PAD⊥平面ABCD，AB⊥AD，
AB平面ABCD，平面PAD∩平面ABCD=AD，
所以AB⊥平面PAD， …………(3分)
又AB平面PAB，所以平面PAB⊥平面PAD. …………(2分)
(2)如图以A为原点，以AB所在直线为x轴，以AD所在直线为y轴建立如图所示直角空间坐标系
A-xyz， …………(1分)
由AB=AP=2，CD= 2 ，PAD=120°，ADC=45°，
则B(2,0,0)，P(0,-1, 3)，设AD=t，则D(0,t,0)，C(1,t-1,0)， …………(2分)
所以CP  1,t, 3 ，CD1,1,0
①设平面PCD的法向量为nx,y,z，由nCP，nCD，得：
xty 3z0  1t
 ，可取n1,1,  …………(2分)
xy0  3 
 
则有：sin cos n,BP ，BP 2,1, 3 ，
33 211t
即： 
44 1t2
413 11
3
化简得：7t230t270
六校联盟期中联考【高二数学】答案及评分标准(第2页,共5页)
{#{QQABCYaEoggAAAAAAAgCAwFyCEKQkgACCSgOAFAEoAAASRNABAA=}#}9
解得t=3或t  舍，
7
所以AD=3 …………(2分)
 4   5 3
因为平面PCD的法向量n  1,1, 3   ，同理可求得平面PBC的法向量n 1    2,1, 3    ……(1分)
nn 29 55
设二面角B-PC-D的夹角大小为，则 cos 1 
n n 220
1
29 55
所以二面角B-PC-D的夹角的余弦值为 …………(2分)
220
18.(17分)
(1)依题意有c=1，a=2，解得b2=a2-c2=3， …………(2分)
x2 y2
所以椭圆的方程为  1. …………(1分)
4 3
1
(2)①设l ：x=my+1(m≠0)，A(x ,y )，B(x ,y )，则l ：x y1m0， …………(1分)
AB 1 1 2 2 CD
m
联立   xmy1 ，故  3m24  y26my90 ， 4m240 ， y y  6m ，
3x24y2 12 1 2 3m24
8
x x my y 2 …………(1分)
1 2 1 2 3m24
m21
由弦长公式可得： AB  1m2 y y 12
2 1 3m24
m21
同理可得： CD 12 ，
4m23
 m21 2
1
所以S = AB CD 72 …………(2分)
四边形ABCD 2  3m24  34m2
72 72 288
令tm21t1，则S    …………(2分)
 1  1 72 1 1 2 49 49
t2 t 
t

2



4
288
当m2=1，S的最小值是 …………(1分)
49
6m 8
②∵y y  ，x x my y 2 …………(1分)
1 2 3m24 1 2 1 2 3m24
 4 3m  1  4m2 3m 
∴M 3m24 , 3m24   ，由 m 代替m，得N  34m2 , 34m2    ， …………(1分)
六校联盟期中联考【高二数学】答案及评分标准(第3页,共5页)
{#{QQABCYaEoggAAAAAAAgCAwFyCEKQkgACCSgOAFAEoAAASRNABAA=}#}4 4m2 4 4 
当
3m24

34m2
，即m2=1时，l
MN
：x
7
，过点K
7
,0

. …………(1分)
4 4m2 7m
当  ，即m2≠1时，K  ，
3m24 34m2 MN 4  m21 
l MN ：y 3m 3 2 m 4  4  m 7 2 m 1     x 3m2 4 4     m2 1,m0 
4 
当y=0，经验证直线MN过点K ,0. …………(3分)
7 
4 
综上，直线MN恒过点K ,0. …………(1分)
7 
19.(17分)
(1)d(A,B) 11 21 5 …………(2分)
OAOB 12 3 10
cos(A,B)cosOA,OB  
OA OB 5 2 10
3 10 103 10
eA,B1cosA,B1  …………(3分)
10 10
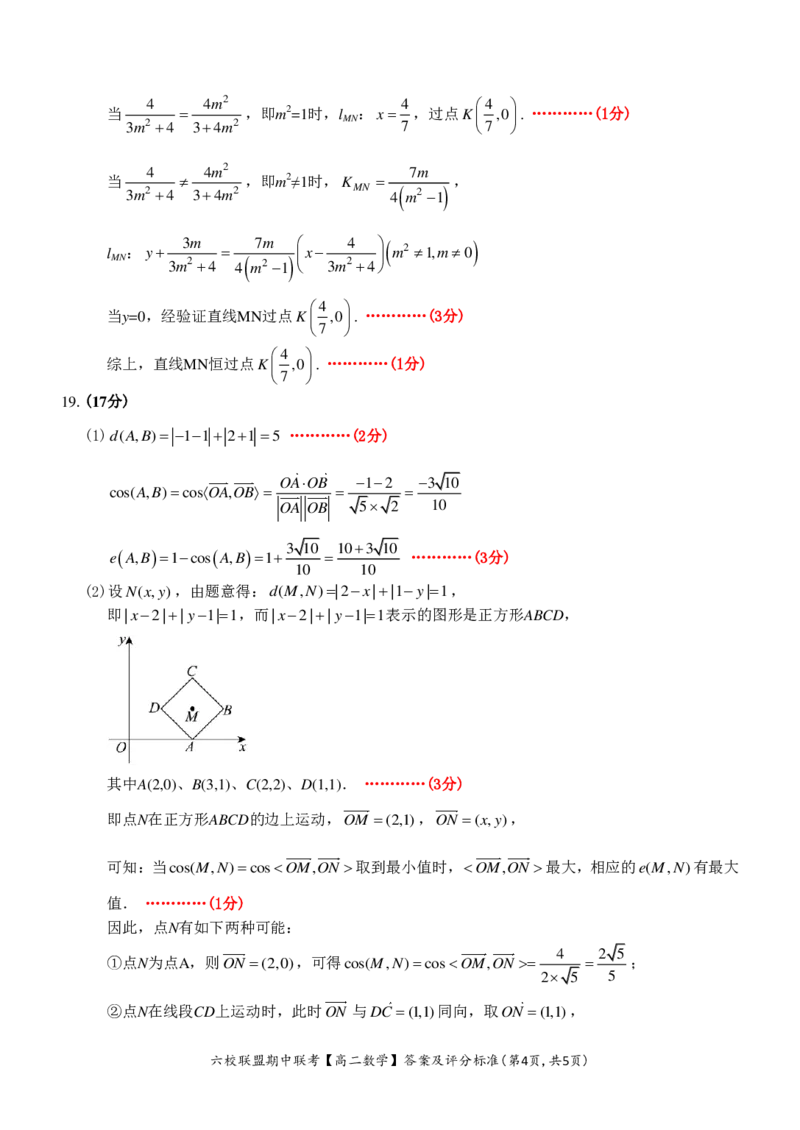
(2)设N(x,y)，由题意得：d(M,N)|2x||1y|1，
即|x2||y1|1，而|x2||y1|1表示的图形是正方形ABCD，
其中A(2,0)、B(3,1)、C(2,2)、D(1,1)． …………(3分)
即点N在正方形ABCD的边上运动，OM (2,1)，ON (x,y)，
可知：当cos(M,N)cosOM,ON 取到最小值时，OM,ON 最大，相应的e(M,N)有最大
值． …………(1分)
因此，点N有如下两种可能：
4 2 5
①点N为点A，则ON (2,0)，可得cos(M,N)cosOM,ON   ；
2 5 5
②点N在线段CD上运动时，此时ON 与DC(1,1)同向，取ON (1,1)，
六校联盟期中联考【高二数学】答案及评分标准(第4页,共5页)
{#{QQABCYaEoggAAAAAAAgCAwFyCEKQkgACCSgOAFAEoAAASRNABAA=}#}3 3 10
则cos(M,N)cosOM,ON   ．
5 2 10
3 10 2 5 2 5
因为  ，所以e(M,N)的最大值为1 ． …………(3分)
10 5 5
1k
(3)易知D(O,P)  ，设P(x,kxk1)，则d(O,P)h(x)|x||kxk1|
min
k21
当k=0时，d(O,P)h(x)|x||1|，则d(O,P) =1，D(O,P) =1，满足题意； …………(2分)
min min
k1
当k≠0时，d(O,P)h(x) x  kxk1  x  k  x ，
k
 k1
由分段函数性质可知d(O,P) min min  h(0),h  k     ，
|1k| k1 k1 1k
又h(0)|1k| 且h   恒成立，当且仅当k=1时等号成立．
k21  k  k k21
综上，满足条件的直线有且只有两条，l:y=1和y=x． …………(3分)
六校联盟期中联考【高二数学】答案及评分标准(第5页,共5页)
{#{QQABCYaEoggAAAAAAAgCAwFyCEKQkgACCSgOAFAEoAAASRNABAA=}#}