数学答案_2024-2025高二（7-7月题库）_2024年11月试卷_1123云南省玉溪市一中2024-2025学年高二上学期期中考试_云南省玉溪市一中2024-2025学年高二上学期期中考试数学试题PDF版含答案

答案
一．选择题。
1 2 3 4 5 6 7 8 9 10 11
C C D A B B A D AC BD ABD
二．填空题
12. 1 13. 13 14. x2  y2  7 ；7
3 2
三．解答题。
15.解;（1）圆心为C （2.0），半径为r  2
1 1
设切线的斜率为k ，则切线的方程为 y 3 k(x4)即：kx y 4k 3 0
所以圆心（2.0）到切线的距离等于半径2
32k 5
即：  2 k  所以切线方程为：5x12y 16  0 或x  4
k2 1 12
（2）C（-2，0），r 8设M（x,y），动圆的半径为r
2 2
所以 MC  2 r，MC 8r  MC  MC 10  4
1 2 1 2
所以M 点的轨迹是以C ,C 为焦点的椭圆
1 2
x2 y2
所以a 5，c  2,b  21，所以轨迹方程为  1.
25 21
2π π 2π
16.解：（1）由函数图象可得A2,T 2(  )π, π,2,即 f x2sin2x，
3 6 
π π π
根据图象可得 2  2kπ,kZ，解得 2kπ,kZ，
6 2 6
π π π
图为|| ，所以 ，所以 f(x)2sin(2x )；
2 6 6
 π  π π π 7π
（2） f x2sin2x ,x

0,

,2x 

,

 6  2 6 6 6 
 π
关于x的方程 f xm0在x 0, 上有两个不同的实数解，
 
 2
则 与ym的图象有两个交点，结合函数图像可知m1,2 .
=  
实数m的取值范围为1,2
.
17.解：因为 3asinCbcacosC ，
由正弦定理可得 3sinAsinCsinBsinCsinAcosC ，
即 3sinAsinCsinAcosC sinCsinAC ，
所以 3sinAsinC sinCsinCcosA ， 
因为 sinC 0 ，所以 3sinA1cosA ，所以 2sinA 1 ，
 6

又因为 0 A ，所以 A .
3
(2)
   
bc sinB-sinC sin（AC）-sinC
2
 
sin(
3
C)sinC
  3cosC-sinC
2sin（C-
3
）
    
a sinA 3 3 3 3
2
 2  
因为 A ,BC  ,0B ,0C ，
3 3 2 2
    
所以 C , C  ，
6 2 6 3 6
  1 1 bc  3 3
所以 sin(C ) ,  ，所以    ，  
3  2 2 a  3 3 
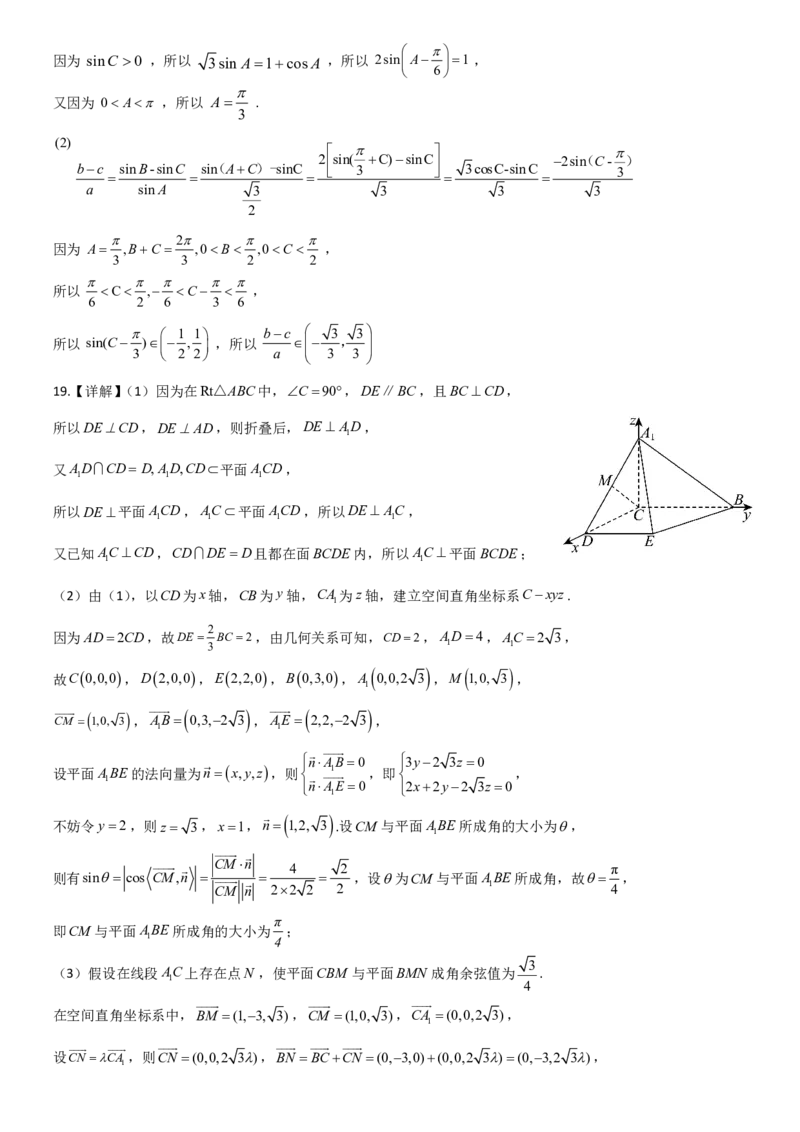
19.【详解】（1）因为在Rt△ABC中，C90，DE∥BC，且BCCD，
所以DECD，DEAD，则折叠后，DE AD，
1
又ADCD D, AD,CD平面ACD，
1 1 1
所以DE平面ACD，AC平面ACD，所以DE AC，
1 1 1 1
又已知ACCD，CDDE D且都在面BCDE内，所以AC 平面BCDE；
1 1
（2）由（1），以CD为x轴，CB为y轴，CA为z轴，建立空间直角坐标系Cxyz.
1
2
因为AD2CD，故DE BC2，由几何关系可知，CD2，AD4，AC2 3，
3 1 1
故C0,0,0，D2,0,0，E2,2,0，B0,3,0，A  0,0,2 3  ，M  1,0, 3  ，
1
C  M    1,0, 3 ，  A  B    0,3,2 3  ，  A  E    2,2,2 3  ，
1 1
r  n    A  B  0  3y2 3z0
设平面A 1 BE的法向量为nx,y,z，则   1  ，即 ，
nAE 0 2x2y2 3z0
1
  
不妨令y2，则z 3，x1，n 1,2, 3 .设CM 与平面ABE所成角的大小为，
1
 
  CMn 4 2 π
则有sin cos CM,n  C  M  n   22 2  2 ，设为CM 与平面A 1 BE所成角，故 4 ，
π
即CM 与平面ABE所成角的大小为 ；
1 4
3
（3）假设在线段AC上存在点N ，使平面CBM 与平面BMN 成角余弦值为 .
1
4
  
在空间直角坐标系中，BM (1,3, 3)，CM (1,0, 3)，CA (0,0,2 3)，
1
     
设CN CA ，则CN (0,0,2 3)，BN BCCN (0,3,0)(0,0,2 3)(0,3,2 3)，
1 
  n BM 0  x 3y  3z 0
设平面BMN 的法向量为n x ,y ,z ，则有 2  ，即 2 2 2 ，
2 2 2 2 n BN 0 3y 2 3z 0
2 2 2
  
不妨令z  3，则y 2，x 63，所以n  63,2, 3 ，
2 2 2 2
 
  n BM 0  x 3y  3z 0
设平面CBM 的法向量为n x ,y ,z ，则有 3  ，即 3 3 3 ，
3 3 3 3 n CM 0 x  3z 0
3 3 3
  
不妨令z  3，则x 3，y 0，所以n  3,0, 3 ，
3 3 3 3
3
若平面CBM 与平面BMN 成角余弦值为 .
4
 
则满足cos n  ,n   n  2    n  3  9183  3 ，
2 3 n n 2 3 9(21)2423 4
2 3
1    1
化简得22310，解得1或 ，即CN CA 或CN  CA ，
2 1 2 1
3
故在线段AC上存在这样的点N ，使平面CBM 与平面BMN 成角余弦值为 . 此时CN的长度为 3 或2 3.
1
4
x2 y2
19.（1）椭圆方程为  1
4 3
（2）根据题意得中点弦的斜率存在，且M 在椭圆内，
设A(x ,y)，B(x ,y )，
1 1 2 2
x2 y2 x2 y2
所以 1  1 1， 2  2 1，
4 3 4 3
(x x )(x x ) (y  y )(y  y )
两式作差，得 1 2 1 2  1 2 1 2 0，
4 3
x x 1 y y
由于M 是BC的中点，故 1 2  , 1 2 1，
2 2 2
x x y  y y y
所以 1 2  1 2 1 2 0，
4 3 x x
1 2
1 2 3
所以  k 0，所以k  ，
4 3 BC BC 8
3 1
所以中点弦的方程为y1 (x )，
8 2
所求的直线方程6x16y190．
（3）当直线l的斜率为0时，显然不满足条件k k 1，
PM PN
当直线l的倾斜角不为0时，
设直线l的方程为：xmy1， ， ，
xmy1   1,  1   2,  2
由 ，可得  3m24  y26my90，
3x24y2 12
由题意Δ36m24  3m24  9144m21440，
6m 9
则y  y  ，y y  ，
1 2 3m24 1 2 3m24y y y y 2my y 3y  y 
由k k  1  2  1  2  1 2 1 2
PM PN x 2 x 2 my 3 my 3 m2y y 3my  y 9
1 2 1 2 1 2 1 2
9 6m
2m 3
3m24 3m24
 m，
9 6m
m2 3m 9
3m24 3m24
由k k 1，即m1，
PM PN
故存在满足条件的直线，直线l的方程为：xy10.