p D. p >p 或p 0,
1 2 3 1 1 1
nn-1
故S =na +
n 1
nn-1
d=na +
2 1
×2a =a n2,
2 1 1
故 S = a n,故 S - S = a 即 S
n 1 n n-1 1 n
为等差数列,
故“2a +a =a”是“ S 为等差数列”的充分条件.
1 2 3 n
若 S n 为等差数列,设其公差为d 1 ,则 S n = a 1 +n-1 d , 1
故S n = a 1 -d 1 +nd 1 2,
故a n =S n -S n-1 = a 1 -d 1 +nd 1 2- a 1 -2d 1 +nd 1 2
=d 12 a 1 -3d 1 +2nd 1 ,其中n≥2.
因为a n 为等差数列,故a 1 也应该符合上式,故a 1 =d 12 a 1 -d 1 ,
·322·故d = a ,故S =n2a ,故a =22a -a =3a ,
1 1 n 1 2 1 1 1
a =32a -22a =5a ,故2a +a =5a =a ,
3 1 1 1 1 2 1 3
故“2a +a =a”是“ S
1 2 3 n
为等差数列”的必要条件.
综上,“2a +a =a”是“ S
1 2 3 n
为等差数列”的充要条件,
故选:C.
x2 y2
8.双曲线 - =1(a,b>0)的左右焦点分别为F,F,P是双曲线右支上一点,点F 关于∠FPF 平分线
a2 b2 1 2 1 1 2
1
的对称点也在此双曲线上,且cos∠FPF= ,则双曲线的离心率为 ( )
1 2 9
21 21
A. B. C. 2 D. 3
4 3
答案 B
【分析】如图,由题意可知PF 1 =PQ 且P,F 2 ,Q三点共线,设PF 1 =m,PF 2 =n,根据双曲线的定义求得
QF 1 =4a,m=3a,n=a,在△PFQ、△FPF 中分别利用余弦定理计算即可求解. 1 1 2
解析 如图,设F 关于∠FPF 平分线的对称点为Q,则该角平分线为线段FQ的垂直平分线,
1 1 2 1
所以PF 1 =PQ ,且P,F 2 ,Q三点共线,设PF 1 =m,PF 2 =n,
则PQ =m,m-n=2a⇒QF 2 =PQ -n=m-n=2a,所以QF 1 =2a+QF 2 =4a,
在△PFQ中,由余弦定理,得cos∠FPF= PF 1
1 1 2
2+PQ 2-QF 1 2
2PF 1 PQ
m2+m2-(4a)2 = ,
2m2
1 m2+m2-(4a)2 1
又cos∠FPF= ,所以 = ,解得m=3a,所以n=a,
1 2 9 2m2 9
在△FPF 中,由余弦定理,得cos∠FPF= PF 1
1 2 1 2
2+PF 2 2-F 1 F 2 2
2PF 1 PF 2
9a2+a2-4c2 1 = = ,
2⋅3a2 9
c 21
整理,得3c2=7a2,由e>1,解得e= = .
a 3
21
即双曲线的离心率为.
3
故选:B
二、选择题:本题共3小题,每小题6分,共18分。在每小题给出的选项中, 有多项符合题目要求。全部选对
的得6分,部分选对的得3分,有选错的得0分。
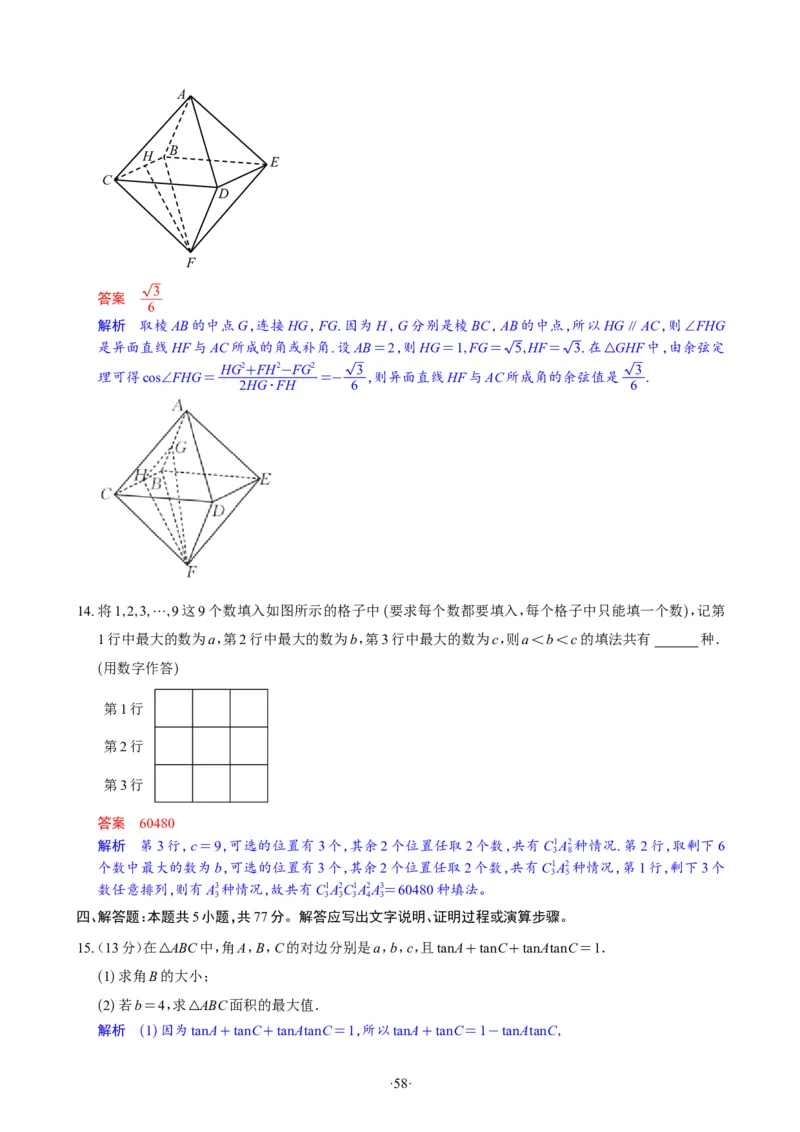
9.如图,八面体的每个面都是正三角形,并且4个顶点A,B,C,D在同一个平面内,如果四边形ABCD是边
长为2的正方形,则 ( )
·323·π 1
A.异面直线AE与DF所成角大小为 B.二面角A-EB-C的平面角的余弦值为
3 3
8π
C.此八面体一定存在外接球 D.此八面体的内切球表面积为
3
答案 ACD
【分析】建立空间直角坐标系,运用坐标法计算异面直线所成角及二面角可判断A项、B项,由|OE|=
|OF|=|OA|=|OB|=|OC|=|OD|可判断C项,运用等体积法求得内切球的半径,进而可求得内切球的
表面积即可判断D项.
解析 连接AC、BD交于点O,连接OE、OF,
因为四边形ABCD为正方形,则AC⊥BD,
又因为八面体的每个面都是正三角形,所以E、O、F三点共线,且EF⊥面ABCD,
所以以O为原点,分别以OB、OC、OE为x轴、y轴、z轴建立空间直角坐标系O-xyz,如图所示,
则O(0,0,0),A(0,- 2,0),B( 2,0,0),C(0, 2,0),D(- 2,0,0),E(0,0, 2),F(0,0,- 2),
对于A项,AE=(0, 2, 2),DF=( 2,0, 2),
设异面直线AE与DF所成角为θ,
则cosθ=cosAE,DF
AE⋅DF
=
AE
DF
2 1
= = ,
2×2 2
π π
所以θ= ,即异面直线AE与DF所成角大小为 ,故A项正确;
3 3
对于B项,BE=(- 2,0, 2),BA=(- 2,- 2,0),BC=(- 2, 2,0),
设面ABE的一个法向量为n=(x ,y ,z ),
1 1 1
则 n n ⋅ ⋅B B A E = = 0 0 ⇒ - - 2 2 x x 1 1 + - 2 2 z y 1 1 = = 0 0 ,取x 1 =1,则y 1 =-1,z 1 =1,则n =(1,-1,1),
设面BEC的一个法向量为m=(x ,y ,z ),
2 2 2
则 n n ⋅ ⋅ B B E C = = 0 0 ⇒ - - 2 2 x x 2 2 + + 2 2 z y 2 2 = = 0 0 ,取x 2 =1,则y 2 =1,z 2 =1,则m =(1,1,1),
·324·
n⋅m
所以cosn,m=
n m
1-1+1 1
= = ,
3× 3 3
又因为面ABE与BEC所成的二面角的平面角为钝角,
1
所以二面角A-EB-C的平面角的余弦值为- ,故B项错误;
3
对于C项,因为|OE|=|OF|=|OA|=|OB|=|OC|=|OD|= 2,
所以O为此八面体外接球的球心,
即此八面体一定存在外接球,故C项正确;
对于D项,设内切球的半径为r,
1 1 8 2
则八面体的体积为V=2V =2× S ⋅EO=2× ×2×2× 2= ,
E-ABCD 3 ABCD 3 3
1 1 1 π 8 3
又八面体的体积为V=8V =8V =8× S ⋅r=8× × ×22×sin ×r= r,
E-ABO O-ABE 3 EAB 3 2 3 3
8 3 8 2 6
所以 r= ,解得r= ,
3 3 3
6
所以内切球的表面积为4πr2=4π×
3
2 8π
= ,故D项正确.
3
故选:ACD.
π
10.函数f(x)=2cos(ωx+φ)ω>0,|φ|<
2
5π
相邻两个最高点之间的距离为π, ,0
12
为f(x)的对称中心,
π
将函数f(x)的图象向左平移 后得到函数y=g(x)的图象,则 ( )
12
5π
A. g(x)在0,
12
上存在极值点
1 π
B.方程g(x)= x-
2 3
4π
所有根的和为
3
π
C.若g(x+m)为偶函数,则正数m的最小值为
12
λ
D.若g x
2
π π
在 ,
3 2
4
上无零点,则正数λ的取值范围为0,
3
16
∪ 5,
3
答案 AC
【分析】根据给定条件,求出函数f(x)及g(x)的解析式,结合余弦函数的图象、性质逐项分析判断得解.
2π 5π
解析 依题意, =π,解得ω=2,由f
ω 12
5π π
=0,得2× +φ=kπ+ ,k∈Z,
12 2
π π π
而|φ|< ,则k=0,φ=- ,f(x)=2cos2x-
2 3 3
π
,g(x)=2cos 2x+
12
π
-
3
π
=2cos2x-
6
,
5π
对于A,当x∈0,
12
π π 2π
时,2x- ∈- ,
6 6 3
π
,显然当2x- =0时,函数g(x)取得极大值,A正确;
6
π
对于B,由g
3
π
=0,得函数y=g(x)的图象关于点 ,0
3
1 π
对称,直线y= x-
2 3
π
过点 ,0
3
,
1 π
因此直线y= x-
2 3
π
与y=g(x)的图象交点关于点 ,0
3
对称,共有2n+1,n∈N个交点,
1 π
即方程g(x)= x-
2 3
2n+1 2n+1 4π
共有2n+1个根,所有根的和为 π,不存在n使得 π= ,B错
3 3 3
误;
π
对于C,函数g(x+m)=2cos2x+2m-
6
π
是偶函数,则2m- =k π,k ∈Z,
6 1 1
k π π π
m= 1 + ,k ∈Z,因此当k =0时,正数m取得最小值 ,C正确;
2 12 1 1 12
λ
对于D,函数g x
2
π
=2cosλx-
6
π π
,当x∈ ,
3 2
π πλ π πλ π
时,λx- ∈ - , -
6 3 6 2 6
,
λ
由g x
2
π π
在 ,
3 2
πλ π πλ π
上无零点,得 - , -
3 6 2 6
π π
⊆ kπ- ,kπ+
2 2
,k∈Z,
·325·πλ π π 4
3 - 6 ≥kπ- 2 λ≥3k-1 2k+ 3 >3k-1
则 ,k∈Z,解得 4 ,k∈Z,显然 ,k∈Z,
πλ π π λ≤2k+ 4
- ≤kπ+ 3 2k+ >0
2 6 2 3
2 7 4
即- 0时,当x<-2,q x <0,当x>-2,q x >0,所以m x 在-∞,-2 上单调递减,在-2,+∞
上单调递增,
又因为x→-∞时,m x
1
→-1<0,m
m
1
=m +1
m
1 1
em-1=mem>0,所以可得mx 先减后增,不符
合题意;
当m<0时,当x<-2,q x >0,当x>-2,q x <0,所以m x 在-∞,-2 上单调递增,在-2,+∞
上单调递减,
所以当x=-2时,m x 有极大值也是最大值m x =-me-2-1≤0,即m≥-e-2,则m∈-e2,0 ;
综上得存在m∈-e2,0 时,hx
π
是“ 旋转函数”,故D正确.
4
故选:BCD.
·326·【点睛】方法点睛:(1)导函数中常用的两种常用的转化方法:一是利用导数研究含参函数的单调性,常化
为不等式恒成立问题.注意分类讨论与数形结合思想的应用;二是函数的零点、不等式证明常转化为函
数的单调性、极(最)值问题处理;(2)利用导数解决含参函数的单调性问题时,一般将其转化为不等式恒
成立问题,解题过程中要注意分类讨论和数形结合思想的应用;(3)证明不等式,构造一个适当的函数,
利用它的单调性进行解题,是一种常用技巧.许多问题,如果运用这种思想去解决,往往能获得简洁明快
的思路,有着非凡的功效.
第II卷(非选择题)
三、填空题:本题共3小题,每小题5分,共15分.
12.有甲乙两生从“物理、化学、生物、政治、历史、地理和技术”七门科目中选三门作为高考选考科目,学生甲
物理和化学两门必选,并在另外的五门中任选一门;学生乙必选政治学科,但一定不选物理、化学,则甲乙
两人有且只有一门选科相同的选科方法总数有 种.(用数字作答)
答案 18
【分析】分学生甲选择政治和不选择政治讨论,结合计数原理求解即可.
解析 若学生甲在另外五门中选择政治,由于学生乙一定不选物理、化学,
所以无论学生乙如何选,甲乙两人一定有且只有一门选科相同,此时有C2=6种;
4
若学生甲在另外五门中不选择政治,此时甲有C1=4种选法,
4
甲乙两人有且只有一门选科相同,则乙有C1C1=3种选法,
1 3
此时共有4×3=12种选法;
综上,甲乙两人有且只有一门选科相同的选科方法总数有12+6=18种,
故答案为:18
13.P是圆C:x2+(y-2)2=1上一动点,A2,0 ,Q为AP的中点,O为坐标原点,则OQ 的最大值为 .
1
答案 2+
2
【分析】写出圆C的参数方程,进而可得点Q坐标,结合两点间距离公式转化为求三角函数的最值即可.
解析 如图所示,
x=cosθ
因为圆C:x2+(y-2)2=1的参数方程为
,
y=2+sinθ
2+cosθ 2+sinθ
所以设点P(cosθ,2+sinθ),则AP的中点Q ,
2 2
,
2+cosθ
所以|OQ|=
2
2 2+sinθ
+
2
2 9+4(sinθ+cosθ) 1 π
= = 9+4 2sinθ+
4 2 4
,
π
当sinθ+
4
1 2 2+1 1
=1时,|OQ|取得最大值为 9+4 2= = 2+ .
2 2 2
1
故答案为: 2+ .
2
·327·14.已知函数 fx 满足 fx = f1-x ,f x 为 fx 的导函数,gx = f x
1 n
+ ,x∈R.若a =g 3 n 2024 ,
则数列a n 的前2023项和为 .
2023
答案
3
【分析】由fx =f1-x ,可得f x =-f 1-x ,从而得gx +g1-x
2
= ,然后利用倒序相加法从
3
而可求解.
解析 由题意知fx =f1-x ,所以f x =-f 1-x ,即f x +f 1-x =0,
又因为gx =f x
1
+ ,所以gx
3
+g1-x =f x +f 1-x
2 2
+ = ,
3 3
1
所以a +a +a +⋯+a =g
1 2 3 2023 2024
2
+g
2024
3
+g
2024
2023
+⋯+g
2024
①,
2023
a +a +a +⋯+a =g
1 2 3 2023 2024
2022
+g
2024
2021
+g
2024
1
+⋯+g
2024
②,
2
2023×
3 2023
将①②两式相加可得:a +a +a +⋯+a = = .
1 2 3 2023 2 3
2023
故答案为: .
3
【点睛】关键点点睛:本题主要是对fx =f1-x 求导后得f x =-f 1-x ,主要能够找到gx +
g1-x
2
= 的关系,再根据倒序相加法从而可求解.
3
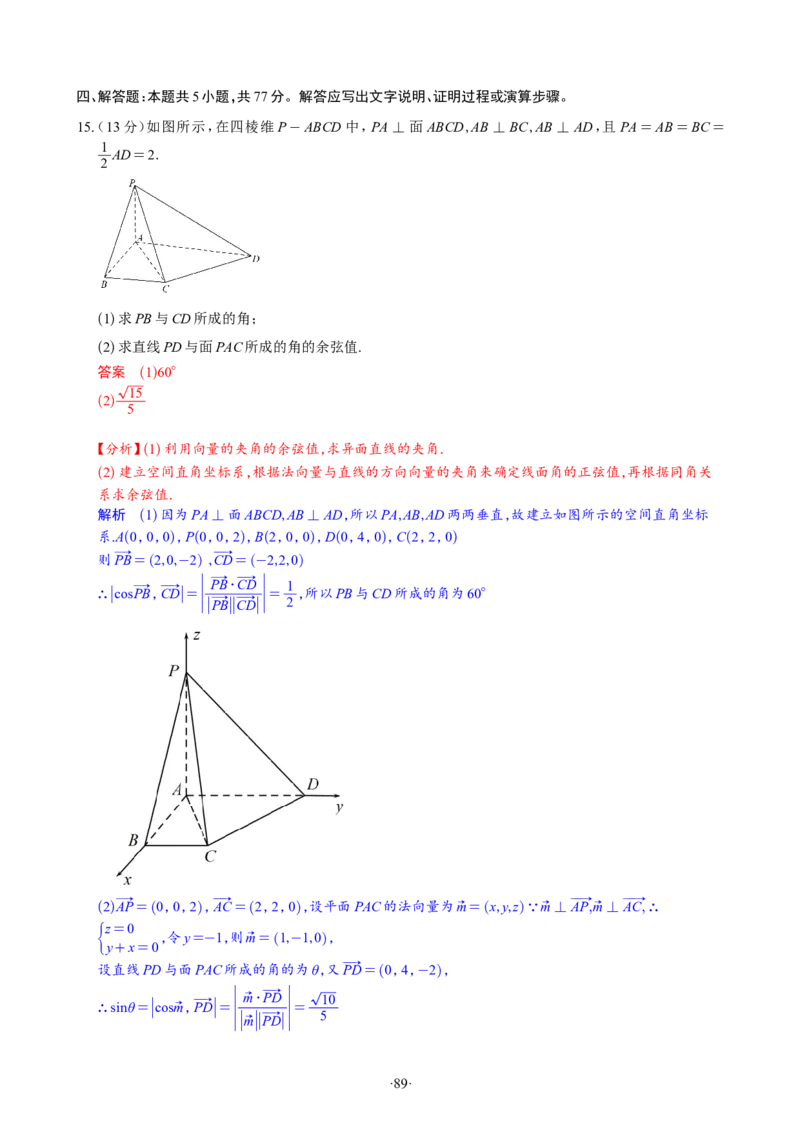
四、解答题:本题共5小题,共77分。解答应写出文字说明、证明过程或演算步骤。
15(. 13分)某校为了解本校学生课间进行体育活动的情况,随机抽取了120名男生和120名女生,通过调查
得到以下数据:120名女生中有20人课间经常进行体育活动,120名男生中有40人课间经常进行体育
活动.
(1)完成如下列联表(单位:人),并判断能否有99.5%的把握认为学生课间经常进行体育活动与性别有关
联.
课间进行体育活动情况
性别 合计
不经常 经常
男
女
合计
(2)以样本的频率作为概率的值,在全校的学生中任取3人,记其中课间经常进行体育活动的人数为X,
求X的分布列与数学期望.
n(ad-bc)2
附:χ2=
a+b c+d a+c b+d
,其中n=a+b+c+d.
α 0.100 0.050 0.010 0.005 0.001
x 2.706 3.841 6.635 7.879 10.828
α
答案 (1)列联表见解析,有关联;
(2)分布列见解析,EX
3
= .
4
·328·【分析】(1)根据已知补全2×2列联表,根据独立性检验,计算χ2的值,与x 对比即可得出答案;
0.005
1
(2)根据已知得出在全校学生中随机抽取1人,其课间经常进行体育活动的概率为 ,则随机变量X的
4
1
所有可能取值为0,1,2,3,且X∼B3,
4
,计算出对应的概率,再结合期望公式求解即可.
解析 (1)补全2×2列联表如下:
课间进行体育活动情况
性别 合计
不经常 经常
男 80 40 120
女 100 20 120
合计 180 60 240
提出零假设H :学生课间经常进行体育活动与性别相互独立,即课间是否经常进行体育活动与性别无
0
关,
240×(80×20-40×100)2 80
依题意,χ2= = ≈8.889>7.879=x ,
120×120×180×60 9 0.005
根据小概率值α=0.005的独立性检验,推断H 不成立,即有99.5%的把握认为学生课间经常进行体育
0
活动与性别有关联;
60 1
(2)由题意得,学生课间经常进行体育活动的频率为 = ,所以在全校学生中随机抽取1人,其课间
240 4
1
经常进行体育活动的概率为 ,
4
1
而随机变量X的所有可能取值为0,1,2,3,则由题意得X∼B3,
4
,
所以PX=k 1 =Ck 3 4 k 1 1- 4 3-k ,k=0,1,2,3,
PX=0 1 =C0× 3 4 0 1 ×1- 4 3 27 = , 64
PX=1 1 =C1× 3 4 1 1 ×1- 4 2 27 = , 64
PX=2 1 =C2× 3 4 2 1 ×1- 4 1 9 = , 64
PX=3 1 =C3× 3 4 3 1 ×1- 4 0 1 = , 64
X的分布列如下:
X 0 1 2 3
27 27 9 1
P
64 64 64 64
所以X的数学期望EX
1 3
=3× = .
4 4
16(. 15分)记△ABC的内角A,B,C所对的边分别是a,b,c,且满足2sinC=3sinA-B .
(1)证明:tanA=5tanB;
5
(2)若△ABC的面积为 c2,求tanC;
12
答案 (1)证明见解析
3
(2)tanC=
2
·329·【分析】(1)根据两角和、差的正弦公式化简后可证tanA=5tanB.
5
(2)根据正弦定理可将面积转化为角的三角函数关系式,化简后可得tanAtanB= tanA+tanB
6
,结合
(1)中结果可求tanC.
解析 (1)由2sinC=3sinA-B 得2sinA+B =3sinA-B ,
则2sinAcosB+2cosAsinB=3sinAcosB-3cosAsinB,
得sinAcosB=5cosAsinB,若cosA=0,则cosB=0,
则A,B均为直角,与题设矛盾,故cosA≠0,故cosB≠0,
故cosAcosB≠0,故tanA=5tanB.
1 5
(2)S = absinC= c2,
△ABC 2 12
5 5 5
所以sinAsinBsinC= sin2C,则sinAsinB= sinC= sinA+B
6 6 6
,
5 5
sinAsinB= sinAcosB+ cosAsinB,
6 6
5
从而tanAtanB= tanA+tanB
6
,
又tanA=5tanB,从而tanB=1,tanA=5,
所以tanC=-tanA+B
tanA+tanB 3
=- = .
1-tanAtanB 2
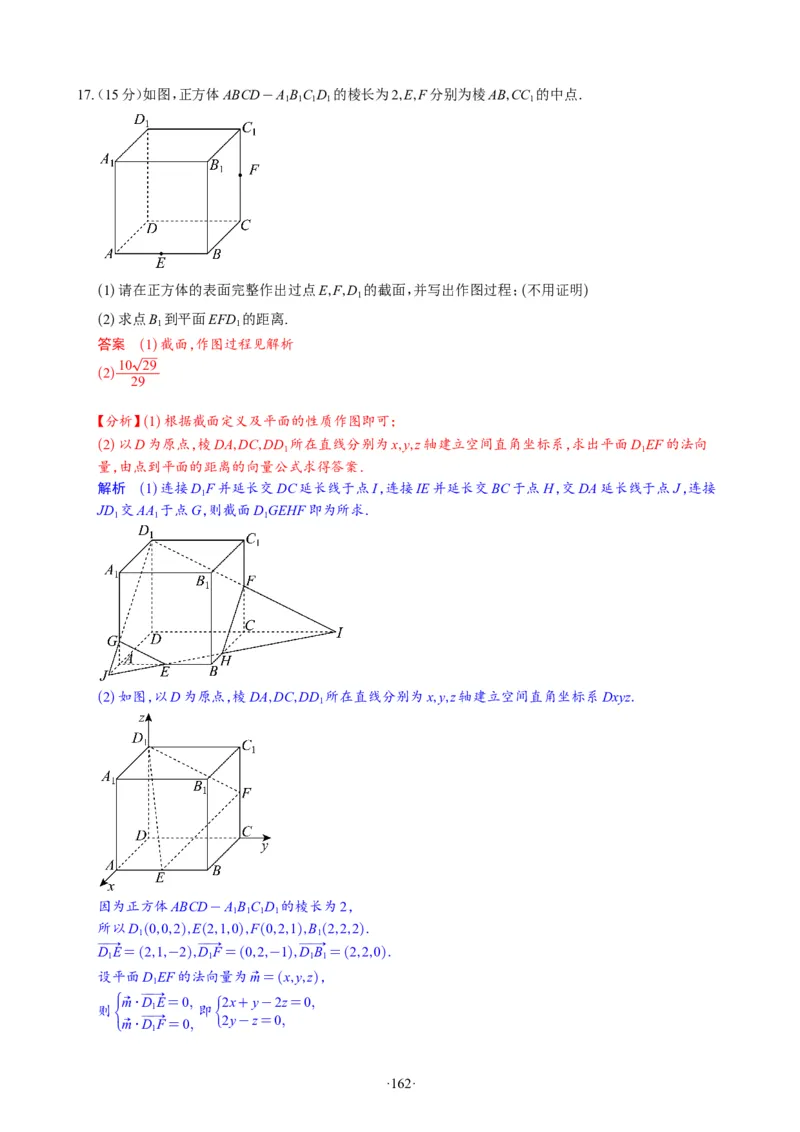
17(. 15分)在三棱锥D-ABC中,AC=3,DC=2 2,∠DCA=45°,CB⊥AB,BC=BD= 6.
(1)证明:平面ADC⊥平面ABC;
33
(2)点E为棱DC上,若BC与平面EAB所成角的正弦值为 ,求DE的长;
11
答案 (1)证明见解析
(2)DE= 2
【分析】(1)如图过D作DH⊥AC,由相似三角形的判定定理与性质求得BH= 2,根据勾股定理的逆定
理可得DH⊥BH,结合面面垂直的判定定理即可证明;
(2)建立如图空间直角坐标系O-xyz,设DE=λDC(0≤λ≤1),根据空间向量的线性运算表示出DE、
AE的坐标,利用空间向量法求线面角建立关于λ的方程,解之即可求解.
解析 (1)过D作DH⊥AC,垂足为H,由AC=3,DC=2 2,∠DCA=45°,
得DH=CH=2,∵CB⊥AB,得AB= AC2-BC2= 3,
AC BC AC AB
由 = ,得△ABC~△BHC,所以 = ,
BC HC BC BH
即AC⋅BH=AB⋅BC,所以BH= 2;
在△BDH中,BH2+DH2=DB2,所以DH⊥BH,
又DH⊥AC,AC∩BH=H,AC,BH⊂平面ABC,
所以DH⊥平面ABC,DH⊂平面ADC,
所以平面ADC⊥平面ABC;
(2)如图以H为原点,HB为x轴,HC为y轴,HD为z轴建立空间直角坐标系O-xyz;
·330·得A0,-1,0 ,B 2,0,0 ,C0,2,0 ,D0,0,2 ,
设DE=λDC,0≤λ≤1,∴DE=0,2λ,-2λ ,
AE=AD+λDE=0,1,2 +0,2λ,-2λ =0,1+2λ,2-2λ
,AB= 2,1,0 ,
设平面ABE的一个法向量为m=x,y,z ,
m⋅AB=0 2x+y=0 则 m ⋅A E =0 ⇒ 1+2λ y+2-2λ ,令x=1,则y=- 2,z= 1+2λ , z=0 2(1-λ)
1+2λ
则m= 1,- 2,
21-λ
,BC=- 2,2,0 ,
设直线BC与平面EAB所成角为θ,则sinθ=cosBC,m
BC⋅m
=
BC⋅
m
-3 2
=
1+2λ 6⋅ 3+
21-λ
=
2
33
,
11
1+2λ
∴
21-λ
2 1+2λ
=8,
21-λ
1
=2 2,∵0≤λ≤1,∴λ= ,
2
所以DE= 2;
x2 y2 1
18(. 17分)已知椭圆 + =1(a>b>0)的长轴长为4,离心率为 ,左顶点为C,过右焦点F作直线与
a2 b2 2
椭圆分别交于A,B两点(异于左右顶点),连接AC,CB.
(1)证明:AC与AF不可能垂直;
(2)求|AB|2+|BC|2+|CA|2的最小值;
答案 (1)证明见解析
999
(2)
32
【分析】(1)求出椭圆方程,设出点A坐标,结合AC⋅AF=0求解即可.
(2)设直线AB方程,联立直线AB方程与椭圆方程,结合韦达定理可表示|AB|2+|BC|2+|CA|2,运用换元法
1
进而将问题转化为求关于 的二次函数的最小值.
m
2a=4
解析 (1)由题意知, c 1 ⇒ c=1 ,
e= = a=2
a 2
x2 y2
又因为b2=a2-c2=3,所以椭圆方程为 + =1,则F1,0
4 3
,C-2,0 ,
证明:设Ax 1 ,y 1
x2 y2
,-2-1),则h0 =0,根据极值点的定义可求得a=1;进而利用导数证明当a
=1时hx ≤0对任意x∈-1,+∞ 恒成立即可;
1
(3)由(2)可得fsin -1
k
1 2n 1
≤sin ,进而 fsin -1
k k
k=n+1
1 1 1
≤sin +sin +⋯+sin .利用导
n+1 n+2 2n
π
数证明不等式sinx-1.
由条件知hx ≤0恒成立,
因为h0 =0,又hx 的图像在定义域上是连续不间断的,
所以x=0是hx 的一个极大值点,则h 0 =0.
又h x
1
=-sinx+ -a,所以h 0
1+x
=1-a=0,得a=1;
下证当a=1时,hx ≤0对任意x∈-1,+∞ 恒成立,
令φx =ln1+x -x,则φ x
1 -x
= -1= ,
1+x 1+x
由φ x >0⇒-10,
知函数φx 在-1,0 单调递增,在0,+∞ 上单调递减,
∴φx ≤φ0 =0,即ln1+x -x≤0,而cosx-1≤0,
所以当x∈0,+∞ 时,hx =cosx-1 + ln1+x -x ≤0.
综上,若fx ≤ax+1恒成立,则a=1.
(3)由(2)可知fx
1
≤x+1,∴fsin -1
k
1
≤sin .
k
2n 1
∴ fsin -1
k
k=n+1
1
=fsin -1
n+1
1
+fsin -1
n+2
1
+⋯+fsin -1
2n
1 1
≤sin +sin +
n+1 n+2
1
⋯+sin ,
2n
π
先证sinx0,函数u(x)单调递增,且u(1)=0,则u(x)0,所以复数z在复平面内对应的点在第三象限.故选C.
2i 2
3.命题“∀x<-1,log x2>0”的否定为 ( )
2
A.∀x<-1,log x2≤0 B.∀x≥-1,log x2>0
2 2
C.∃x≥-1,log x2>0 D.∃x<-1,log x2≤0
2 2
答案 D
解析 全称量词命题的否定为存在量词命题,所以“∀x<-1,log x2>0”的否定为“∃x<-1,log x2≤0”.
2 2
故选D.
x2 y2
4.若双曲线 - =1(a>0,b>0)的实轴长为2,离心率为 3,则双曲线的左焦点F到一条渐近线的距
a2 b2
离为 ( )
A. 2 B.2 2 C.1 D.2
答案 A
c
解析 设双曲线的焦距为2c,由题,a=1,e= = 3,得c= 3,故b2=c2-a2=2,所以F- 3,0
a
,不妨
2×- 3
取渐近线y= 2x,则左焦点F到渐近线y= 2x的距离为
= 2.故选A.
2+1
5.已知上底面半径为 2,下底面半径为2 2的圆台存在内切球(与上、下底面及侧面都相切的球),则该圆
台的体积为 ( )
14 6π 56π
A.14 6π B.56π C. D.
3 3
答案 D
解析 由题可得圆台的母线长为3 2,所以高h= (3 2)2-(2 2- 2)2=4,所以该圆台的体积V=
·335·1
×4×2π+8π+ 2π×8π
3
56π
= ,故选D.
3
6.已知实数m,n满足1>m>n>0,设a=mlnn,b=nlnm,c=nlnn,则 ( )
A.a=b>c B.a>b>c C.c>a>b D.c>a=b
答案 D
解析 因为1>m>n>0,所以lnm>lnn,又y=nx为减函数,所以nlnma=b,故选D.
2π
7.在△ABC中,D为边BC上一点,∠DAC= ,AD=4,AB=2BD,且△ADC的面积为4 3,则sin∠ABD
3
= ( )
15- 3 15+ 3 5- 3 5+ 3
A. B. C. D.
8 8 4 4
答案 A
1 1 3
解析 S = ×AD×AC×sin∠DAC= ×4×AC× =4 3,解得AC=4,所以△ADC为等腰三
△ADC 2 2 2
π 5π AB BD 2BD
角形,∠ADC= ,故∠ADB= ⋅△ABD中,由正弦定理得 = ,即 =
6 6 sin∠ADB sin∠BAD 1
2
BD 1 5π 15
,得sin∠BAD= .因为∠ADB= ,所以∠BAD为锐角,故cos∠BAD= ,故sin∠ABD
sin∠BAD 4 6 4
=sin∠ADC-∠BAD
π
=sin -∠BAD
6
1 3 15- 3
= cos∠BAD- sin∠BAD= .故选A.
2 2 8
8.已知等差数列a n
2n2 2m2
的前n项和为S ,若m≠n,且a +a = ,a +a = ,则S = ( ) n 1 m m 1 n n m+n
A.(m+n)2 B.-(m+n)2 C.m2-n2 D.n2-m2
答案 B
解析 由题, ma 1 +a m =n2=S , na 1 +a n
2 m
mm-1 =m2=S ,所以a m+
2 n 1
nn-1 d=n2①,a n+
2 1
d
2
=m2②,两式作差得a 1m-n
m2-n2-m+n m+n-1
+ 2 d=n2-m2,化简得a 1 + 2 d=-m+n ,即a 1
m+n
m+n
+
m+n-1
d=-(m+n)2,所以S =-(m+n)2,故选B. 2 m+n
二、选择题:本题共3小题,每小题6分,共18分。在每小题给出的选项中, 有多项符合题目要求。全部选对
的得6分,部分选对的得3分,有选错的得0分。
9.下列说法正确的是 ( )
A.若随机变量X∼B2,0.2 ,则PX=2 =0.2
B.若经验回归方程y=bx+a中的b>0,则变量x与y正相关
C.若随机变量ξ∼N0,σ2
1
,且Pξ<-
2
1
=p,则P0<ξ<
2
1
= -p
2
D.若事件A与B为互斥事件,则A的对立事件与B的对立事件一定互斥
答案 BC
解析 P(X=2)=C2(0.2)2=0.04,A错误;若经验回归方程y=bx+a中斜率b>0,则变量x与y正相
2
1 1
关,B正确;易得正态曲线关于直线x=0对称,故P(x>0)= ,又Pξ>
2 2
1
=Pξ<-
2
=p,所以
·336·1
P0<ξ<
2
1
= -p,C正确;掷一枚骰子,设事件A:出现的点数为1,事件B:出现的点数为2,则A
2
与B互斥,但A与B不互斥,D错误.故选BC.
10.已知函数fx
x
=2sinxcos2 ,则以下结论正确的是 ( )
2
A.π为fx 的一个周期 B. fx
π 3π
在- ,
2 2
上有2个零点
C. fx
π
在x=- 3 处取得极小值 D.对∀x 1 ,x 2 ∈R, fx 2 -fx 1 ≤ 3
答案 BC
解析 fx+π =2sinx+π
x+π
cos2
2
x
=-2sinxsin2 ≠fx
2
,A错误;令fx =0,得sinx=0或
x π 3π
cos =0,当x∈- ,
2 2 2
时,解得x=0或x=π,故fx
π 3π
在- ,
2 2
上有2个零点,B正确;fx =
x
2sinxcos2 =sinx+sinxcosx,f x
2
=2cos2x+cosx-1,令f x
1
=0,得cosx=-1或cosx= ,且当x∈
2
π
-π,-
3
时,f x <0,fx
π
单调递减,当x∈- ,0
3
时,f x >0,fx 单调递增,所以fx 在x=
π
- 处取得极小值,C正确;可知fx
3
π
的极大值为f2kπ+
3
3 3
= ,k∈Z,这个极大值即为函数的最
4
大值,fx
π
的极小值为f2kπ- 3
3 3
=- ,k∈Z,这个极小值即为函数的最小值,故∀x ,x ∈R, 4 1 2
fx 2 -fx 1
3 3
≤ ,D错误.故选BC. 2
11.已知定义在R上的函数y=f2x+2
1
为奇函数,且对∀x∈R,都有fx+
2
3
=f -x
2
,定义在R上
的函数f x 为fx 的导函数,则以下结论一定正确的是 ( )
A. fx+2
7
为奇函数 B. f
2
1
=f
2
1
C. f
2
3
=-f
2
D. f x 为偶函数
答案 ACD
解析 因为f2x+2 为奇函数,所以f-2x+2 =-f2x+2 ,所以f-x+2 =-fx+2 ,故
fx+2
1
为奇函数,A正确;又fx+
2
3
=f -x
2
,故fx+1 =f1-x ,所以fx =f2-x =
-fx+2 ,故fx+4 =fx ,所以fx
7
是以4为周期的周期函数,所以f
2
1
=f-
2
,且不能确定
1
f
2
1
=f-
2
一定成立,故B错误;因为fx+1 =f1-x ,所以f x+1 =-f 1-x
1
,所以f
2
3
=-f
2
,C正确;因为f-x+2 =-fx+2 ,所以f -x+2 =f x+2 ,故f -x =f x+4 ,又f
x =f x+4 ,所以f -x =f x ,所以f x 为偶函数,D正确,故选ACD.
第II卷(非选择题)
三、填空题:本题共3小题,每小题5分,共15分.
1
12.小明上学要经过两个有红绿灯的路口,已知小明在第一个路口遇到红灯的概率为 ,若他在第一个路口
4
3
遇到红灯,第二个路口没有遇到红灯的概率为 ,在第一个路口没有遇到红灯,第二个路口遇到红灯的
4
1
概率为 ,则小明在第二个路口遇到红灯的概率为 .
4
1
答案
4
解析 记“小明在第一个路口遇到红灯”为事件A,“小明在第二个路口遇到红灯”为事件B,则P B A
·337·3
= ,P B
4
A
1
= ,又PA
4
3
= ,PA
4
1
= ,所以PB
4
=PA P B A
+PA P B
A
1 1 3
= × + ×
4 4 4
1 1
= .
4 4
π
13.已知α,β∈0,
2
,若P=sinαsin2β+cosαcosβ,则P的最大值为 .
5
答案
4
解析 P= sin22β+cos2βsinα+φ
cosβ 1
,其中tanφ= = ,所以sinα+φ
sin2β 2sinβ
的最大值为1,设t=
5 5 5
sin22β+cos2β= -4cos4β+5cos2β,当cos2β= 时,t取得最大值 ,所以P的最大值为 .
8 4 4
14.已知抛物线C:x2=2py(p>0)的焦点为F,直线l与抛物线C相切于点P(异于坐标原点O),与x轴交于
点Q,若PF =2,FQ
=1,则p= ;向量FP与PQ的夹角为 .
5π
答案 1;
6
p
解析 由题得F0,
2
t2
,设Pt,
2p
x2 x t
,由x2=2py得y= ,求导得y= ,所以直线l的斜率k= ,则直
2p p p
t2 t
线l的方程为y- = x-t
2p p
t
,易得Q ,0
2
,所以PF
t2 p
= + =2,FQ
2p 2
t2 p2
= + =1,解得p
4 4
= 1,t =± 3.当 t = 3 时,FP = 3,1
3 3
,PQ = - ,-
2 2
,则 cosFP,PQ
FP⋅PQ
=
FP
PQ
=
3
- FP,PQ
2
∈0,π
5π 5
,故向量FP与PQ的夹角为 ,当t=- 3时,同理可得夹角为 π.(第一空2
6 6
分,第二空3分)
四、解答题:本题共5小题,共77分。解答应写出文字说明、证明过程或演算步骤。
15.(13分)已知函数fx
1
=ax+ .
ex
(1)讨论fx 的单调性;
(2)若直线y=1与曲线y=fx 相切,求a的值.
解析 (1)fx 的定义域为R,f x
1
=a- ,
ex
当a≤0时,f x <0,fx 单调递减;
当a>0时,令f x =0,得x=-lna,
当x∈-∞,-lna 时,f x <0,fx 单调递减;
当x∈-lna,+∞ 时,f x >0,fx 单调递增.
综上,当a≤0时,fx 在R上单调递减;
当a>0时,fx 在-∞,-lna 上单调递减;在-lna,+∞ 上单调递增.
(2)由题,f x
1
=a- ex ,设切点为 x 0 ,fx 0 ,则f x 0
1
=a- =0, ex0
易知a>0,故x =-lna.
0
又fx 0
1
=1,即ax + =1,将x =-lna代入,得a-alna-1=0. 0 ex0 0
设hx =x-xlnx-1(x>0),则h x =-lnx.
当x∈0,1 时h x >0,hx 单调递增;
当x∈1,+∞ 时h x <0,hx 单调递减.
所以hx ≤h1 =0,所以a=1.
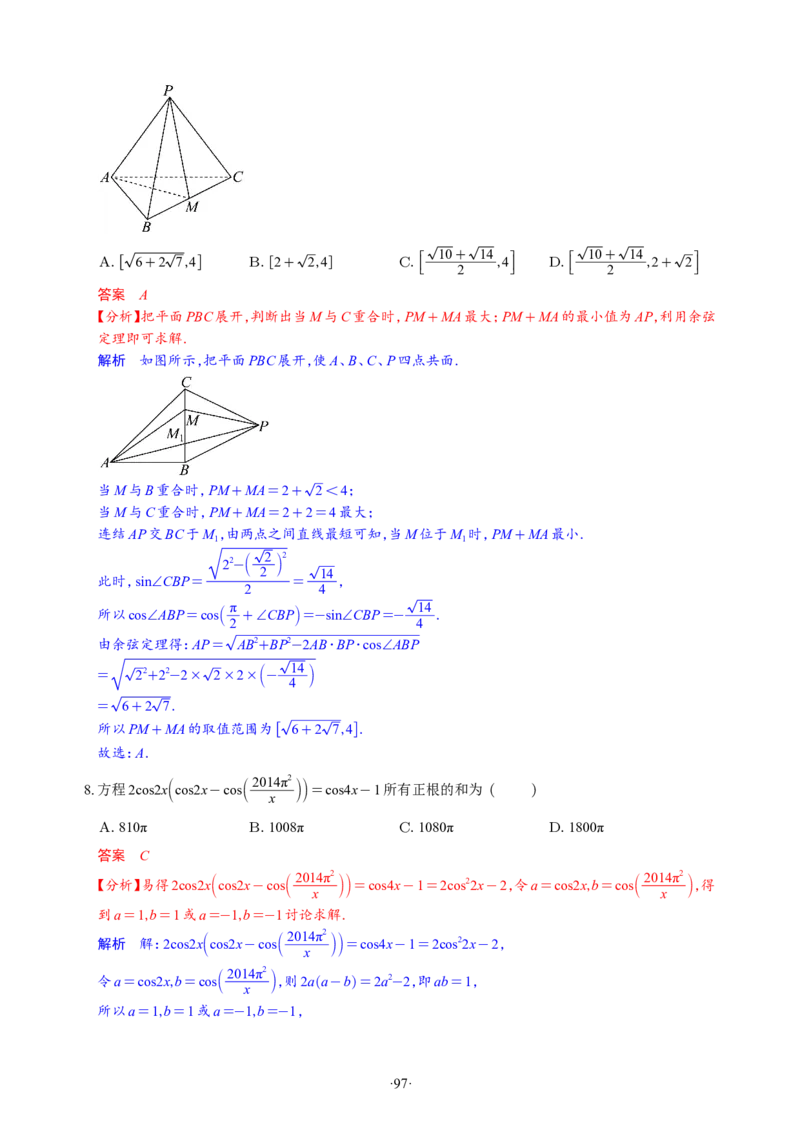
·338·π
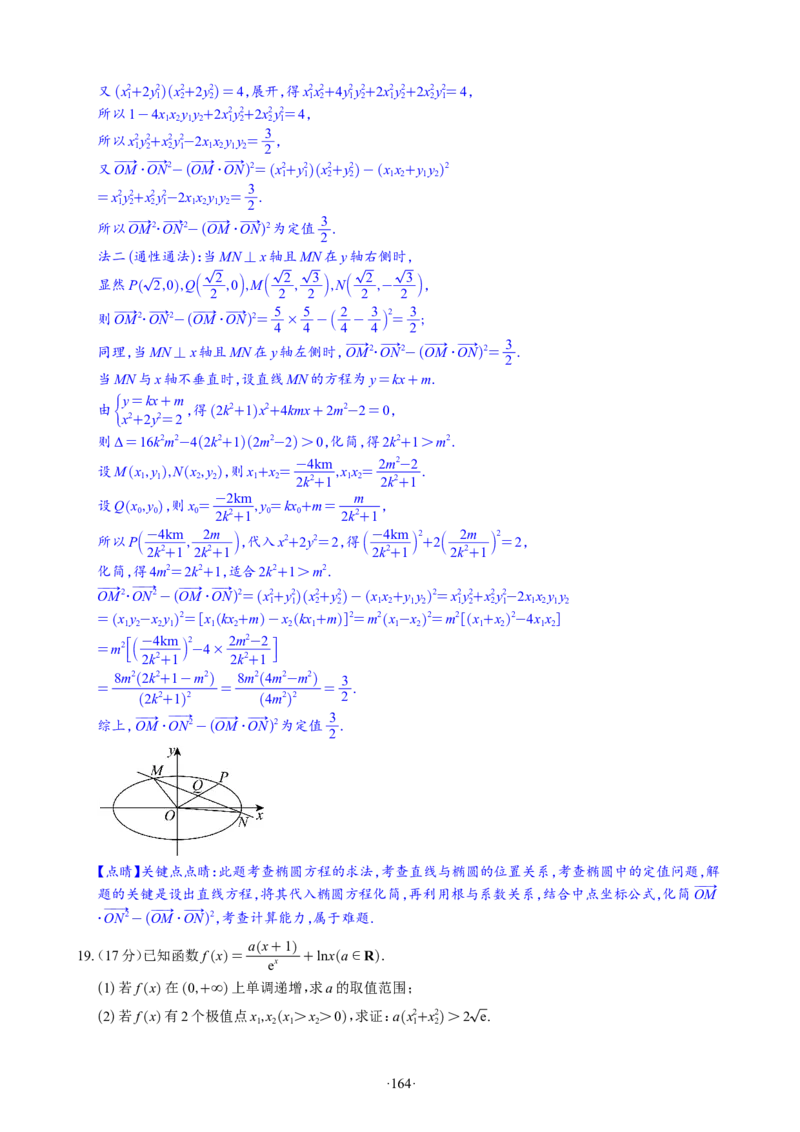
16.(15分)如图,在三棱台ABC-A B C 中,AB=AC=2A B =2AA =4 2,∠A AB=∠A AC= ,∠BAC
1 1 1 1 1 1 1 1 3
π
= .
2
(1)证明:A A⊥B C ;
1 1 1
(2)求直线BB 与平面A ACC 所成角的正弦值.
1 1 1
解析 (1)证明:取BC中点D,连接A B,A C,A D,AD.
1 1 1
因为AB=AC,所以AD⊥BC.
π
因为∠A 1 AB=∠A 1 AC= 3 ,AB=AC,且A 1 A是公共边,所以△A 1 AB≌△A 1 ACSAS ,
所以A B=A C,
1 1
所以A D⊥BC.
1
因为AD∩A D=D,AD,A D⊂平面A AD,所以BC⊥平面A AD.
1 1 1 1
又因为A A⊂平面A AD,
1 1
所以A A⊥BC.
1
又BC∥B C ,
1 1
所以A A⊥B C
1 1 1
(2)解:如图,过点A 作AD的垂线,垂足为O,过点O作OF垂直于AB,垂足为F,连接A F.不难得出,
1 1
π
AB⊥A O,OF∩A O=O,则AB⊥平面A OF.又A F⊂平面A OF,则AB⊥A F.由∠A AF= ,
1 1 1 1 1 1 1 3
π
∠BAC= ,可得AF=OF= 2,AO=A O=2,OD=2,BD=4.
2 1
过点O作BC的平行线,交AB于点E,由(1)得OE,OD,OA 三条直线两两垂直,分别以OE,OD,OA 为
1 1
x,y,z轴建立空间直角坐标系,则A0,-2,0 ,C-4,2,0 ,A 10,0,2 ,B4,2,0 ,B 12,2,2
,AA 1 =0,2,2 ,
AC=-4,4,0
,BB 1 =BA+AA 1 +A 1 B 1 =-2,0,2 .
设平面A 1 ACC 1 的一个法向量为m=x,y,z ,
则 m ⋅A A 1 =0, 即 2y+2z=0,
m⋅AC=0, -4x+4y=0.
令x=1,得y=1,z=-1,所以m=1,1,-1 .
又直线BB 1 的一个方向向量n=-2,0,2 ,
·339·
所以cosm,n
m⋅n
= m ⋅n
-4 6
= =- , 3×2 2 3
6
所以直线BB 与平面A ACC 所成角的正弦值为 .
1 1 1 3
17.(15分)某数学兴趣小组模拟“刮刮乐”彩票游戏,每张彩票的刮奖区印有从10个数字1,2,3,⋯,10中
随机抽取的3个不同数字,刮开涂层即可兑奖,中奖规则为:若3个数的积为3的倍数且不为5的倍数
时,中三等奖;若3个数的积为5的倍数且不为3的倍数时,中二等奖;若3个数的积既为3的倍数,又为
4的倍数,且为7的倍数时,中一等奖;其他情况不中奖.
(1)随机抽取一张彩票,求这张彩票中奖的概率;
(2)假设每张彩票售价为aa∈N* 元,且三、二、一等奖的奖金分别为5元,10元,50元,从出售该彩票
可获利的角度考虑,求a的最小值.
解析 (1)获得三等奖的概率P= C 3 3+C 3 2C 5 1+C 2 1C 2 1+1+C 3 1C 4 2
3
13 = ;
C3 40
10
C1C2+C2C1 5
获得二等奖的概率P= 2 5 2 5 = ;
2 C3 24
10
C1C1C1+C1C1C1 1
获得一等奖的概率P= 1 2 2 1 1 4 = .
1 C3 15
10
79
所以随机抽取一张彩票,这张彩票中奖的概率P=P+P+P= .
1 2 3 120
(2)一张彩票的奖金ξ的取值可能为0,5,10,50元,其分布列为:
ξ 0 5 10 50
2 13 5 1
P
5 40 24 15
所以ξ的期望Eξ
2 13 5 1 169
=0× +5× +10× +50× = .
5 40 24 15 24
若盈利,需a>Eξ
169
= ,
24
因为a∈N*,故a的最小值为8.
x2 y2
18.(17分)已知椭圆C: + =1的右焦点为F,A为椭圆上一点,O为坐标原点,直线OA与椭圆交于另
4 3
一点B,直线AF与椭圆交于另一点D(点B、D不重合).
3
(1)设直线AD,BD的斜率分别为k ,k ,证明:k ⋅k =- ;
AD BD AD BD 4
(2)点P为直线x=4上一点,记PA,PF,PD的斜率分别为k ,k ,k ,若k +2k +k =4,求点P的坐标.
1 2 3 1 2 3
解析 (1)证明:设Dx 0 ,y 0 ,Ax 1 ,y 1 ,则B-x 1 ,-y 1 ,
y -y y +y y2-y2
则k ⋅k = 0 1 × 0 1 = 0 1.
AD BD x -x x +x x2-x2
0 1 0 1 0 1
x2 y2 x2 y2
又 1 + 1 =1, 0 + 0 =1,
4 3 4 3
x2-x2 y2-y2
两式作差得: 0 1 + 0 1 =0,
4 3
y2-y2 3
即 0 1 =- ,
x2-x2 4
0 1
3
所以k ⋅k =- ,得证.
AD BD 4
·340·(2)解:由题,A不与长轴两端点重合,设P4,m ,m≠0,直线AF:x=ty+1,
与椭圆方程联立,并消去x得3t2+4
y2+6ty-9=0.
设Ax 1 ,y 1 ,Dx 2 ,y 2
-6t -9
,则y +y = ,y y = , 1 2 3t2+4 1 2 3t2+4
m-0 m
所以k = = ,
2 4-1 3
k +k = m-y 1 + m-y 2 = 4-x 2
1 3 4-x 4-x 1 2
m-y 1 +4-x 1 m-y 2
4-x 1 4-x 2
.
又x =ty +1,x =ty +1,代入上式化简得
1 1 2 2
6m-3+tm k +k =
1 3
y 1 +y 2 +2ty y 1 2
9-3ty 1 +y 2
3+tm
6m+
=
+t2y y 1 2
×6t 18t
-
3t2+4 3t2+4 2mt2+2m 2m = = ,
18t2 9t2 3t2+3 3 9+ -
3t2+4 3t2+4
4m
所以k +2k +k = =4.故m=3,
1 2 3 3
所以点P的坐标为4,3 .
19.(17分)在数列a n 中,若存在常数t,使得a n+1 =a 1 a 2 a 3 ⋯a n +tn∈N* 恒成立,则称数列a n 为“Ht 数
列”.
1
(1)若c n =1+ n ,试判断数列c n 是否为“Ht 数列”,请说明理由;
(2)若数列a n 为“Ht 数列”,且a 1 =2,数列b n
n
为等比数列,且a2 i =a n+1 +log 2 b n -t,求数列b n
i=1
的
通项公式;
(3)若正项数列a n 为“Ht 数列”,且a >1,t>0,证明:lna 1,t>0,则a =a +t>a >1,故a =a a +t>a a >1,
1 2 1 1 3 1 2 1 2
以此类推,可得对∀n∈N*,a >1,
n
所以fa n b>0)的焦距为2,且ab= 6,则C的离心率为 ( )
a2 b2
1 1 2 3
A. B. C. D.
2 3 2 3
答案 D
c 3
解析 根据题意有半焦距c=1,故a2=b2+c2=b2+1,且ab= 6,故a= 3,C的离心率e= = .
a 3
4.乒乓球被誉为我国的“国球”,一个标准尺寸乒乓球的直径是40mm,其表面积约为 ( )
A.3000mm2 B.4000mm2 C.5000mm2 D.6000mm2
答案 C
解析 标准乒乓球的半径R=20mm,故表面积S=4πR2≈5000mm2.
5.已知函数fx =x3-ax2+x+1没有极值点,则a的取值范围是 ( )
A. - 3, 3 B. - 3, 3 C. -∞,- 3 D. 3,+∞
答案 B
解析 f x =3x2-2ax+1,若fx 没有极值点,则方程f x =0至多只有一个解,
即Δ=4a2-12≤0,故a的取值范围是- 3, 3 .
6.已知α,β∈0,π
cos2β
,且sinα= ,cosα=sinβtanβ,则 ( )
sinβ
π π
A.α=β B.α+β=π C.α-β= D. β-α=
2 2
答案 A
cos2β
解析 由sinα= ,可得cos2β=sinαsinβ,由cosα=sinβtanβ,可得cosαcosβ=sin2β,故cosαcosβ+
sinβ
·343·sinαsinβ=cosα-β =sin2β+cos2β=1,故当α,β∈0,π 时,α=β.
6
7.已知一组样本数据x ,x ,⋯,x 的方差为10,且(-1)ix=-1.5.设y=x+(-1)i(i=1,2,⋯,6),则样本数
1 2 6 i i i
i=1
据y ,y ,⋯,y 的方差为 ( )
1 2 6
A.9.5 B.10.5 C.9.75 D.10.25
答案 B
1 6
解析 设样本数据x ,x ,⋯,x 的平均数为x,则 x-x
1 2 6 6 i
i=1
2=10,设样本数据y ,y ,⋯,y 的平均数为y,
1 2 6
因为y i =x i +(-1)i i=1,2,⋯,6
1 6
,所以y=x,所以 y-y 6 i
i=1
1 6
2= x+(-1)i-x 6 i
i=1
2=10+
1 6
(-1)i x-x
3 i
i=1
1 6
+1=11+ (-1)ix=10.5.
3 i
i=1
8.甲、乙、丙三名同学报名参加数学、物理、化学、生物兴趣小组.-已知每人参加两个兴趣小组,三人不能同
时参加同一个兴趣小组,每个兴趣小组至少有一人参加,则不同的报名参加方式共有 ( )
A.45种 B.81种 C.90种 D.162种
答案 C
解析 方法1:根据题意可知有2个兴趣小组各有2个人报名,有2个兴趣小组各有1个人报名,则共有
C2种;若有2个同学所报名的2个兴趣小组完全相同,则剩下的1个同学所报名参加的2个兴趣小组都
4
只有1个人报名,则有C2种;若三人中只有一人所报名的2个兴趣小组各有2人报名,则另两人每人各报
3
名一个有2人报名的兴趣小组和一个仅有1人报名的兴趣小组,则有C1⋅A2⋅A2=12种,故一共有C2
3 2 2 4
C2+C1⋅A2⋅A2
3 3 2 2
=90种.
方法2:甲乙完全相同的报名参加方式有C2C2=6种,甲、乙只有一个兴趣小组相同的报名参加方式有C2
4 2 4
C1C1C1=48种,甲、乙完全不同的报名参加方式有C2C2=36种,所以他们不同的报名参加方式共有6+
2 2 2 4 4
48+36=90种.
二、选择题:本题共3小题,每小题6分,共18分。在每小题给出的选项中, 有多项符合题目要求。全部选对
的得6分,部分选对的得3分,有选错的得0分。
9.已知函数fx
π
=2cosx-
6
+1,则 ( )
A. fx 的最小正周期是2π B. fx 的值域是-1,3
C. y=fx
π
的图像关于点 ,1
3
对称 D. y=fx
π
的图像关于直线x= 对称
6
答案 ABD(选对部分得3分)
解析 fx
π
=2cosx-
6
+1,故fx 的最小正周期是2π,值域为-1,3
π
,A,B正确;因为f
3
≠1,
故fx
π
不关于点 ,1
3
π
对称,C错误;因为x= 是fx
6
的极大值点,故fx
π
关于直线x= 对称,D
6
正确.
10.已知点A4,1
x2 y2
,F,F 分别为双曲线C: - =1的左、右焦点,P为C的右支上一点,则 ( ) 1 2 2 7
A. PA +PF 1 <6 2 B. PA +PF 2 ≥3 2
C. PA -PF 1 ≤- 2 D. PA -PF 2 >- 2
·344·答案 BCD(选对部分得3分)
解析 当P的横坐标为无穷大时,PA +PF 1 也为无穷大,故A错误;由双曲线的定义可知PF 1 -PF 2
=2a=2 2,故PA +PF 2 =PA +PF 1 -2 2≥AF 1 -2 2=3 2,故B正确;PA -PF 1 =PA -
PF 2 -2 2≤AF 2
7
-2 2=- 2,故C正确;C的一条渐近线的斜率为 ,大于直线AF 的斜率,所以 2 2
当P在x轴上方时,A,P,F 2 不可能共线,故由三角形三边关系可知PA -PF 2 >-AF 2 =- 2,故D正
确.
11.在△ABC中,AB=AC=5,BC= 50,边AB,AC在平面α上的射影长分别为3,4,则边BC在α上的射影
长可能为 ( )
A.7 B.6 C.1 D.0
答案 AC(选对部分得3分)
解析 不妨设点A在α上,因为AB=AC=5,且边AB,AC在平面α上的射影长分别为3,4,所以点B,C
到α的距离分别为4,3.当B,C在α同一侧时,BC在α上的射影长为 ( 50)2-(4-3)2=7;当B,C在α
不同侧时,BC在α上的射影长为 ( 50)2-(4+3)2=1.
第II卷(非选择题)
三、填空题:本题共3小题,每小题5分,共15分.
12.已知向量a=k,2
,b=1,1
,若b⊥b-a
,则k= ,a+b = .
答案 0, 10(第一空3分,第二空2分)
解析 因为向量a=k,2
,b=1,1
,所以b-a=1-k,-1
,当b⊥b-a
时,b⋅b-a =0,即1-k
-1=0,故k=0,所以a+b=1,3
,a+b = 12+32= 10.
13.记S n 为等差数列a n 的前n项和,若a =3,S =25,则S = . 2 5 7
答案 49
解析 因为S =5a =25,则a =5,又因为a =3,故a =2a -a =7,所以
5 3 3 2 4 3 2
S =7a =49.
7 4
14.已知a>0且a≠1,函数 f x
2ax
= -x在0,+∞
ax-1
的最大值为-3,则 f x 在-∞,0 的最小值为
.
答案 方法1:因为 fx + f-x
2ax 2a-x 2ax 2
= + = + =2,所以y= fx
ax-1 a-x-1 ax-1 1-ax
的图像关于点
0,1 对称,故若fx 在0,+∞ 的最大值为-3,则fx 在-∞,0 的最小值为5.
2ax 2
解析 方法2:由条件得,当x>0时, -x≤-3,且等号成立,即2+ -x≤-3,
ax-1 ax-1
2
∴ -x≤-5,∴f-x
ax-1
2a-x 2
= +x=- -x
a-x-1 ax-1
≥5,且等号成立,∴fx 在-∞,0 的最小值
为5.
四、解答题:本题共5小题,共77分。解答应写出文字说明、证明过程或演算步骤。
15.(13分)
记△ABC的内角A,B,C的对边分别为a,b,c,已知2b=c.
(1)若cosB=sinC,求tan2B;
·345·3
(2)若cosA= ,a= 2,求△ABC的面积.
4
解析 (1)因为2b=c,由正弦定理可得:
2sinB=sinC,
因为cosB=sinC,
所以2sinB=cosB,
sinB 1
故tanB= = .
cosB 2
2tanB 4
所以tan2B= = .
1-tan2B 3
(2)由余弦定理可知a2=b2+c2-2bccosA,
即2=b2+4b2-3b2=2b2,
故b=1,c=2.
7
又sinA= 1-cos2A= ,
4
1 1 7 7
所以S = bcsinA= ×1×2× = .
△ABC 2 2 4 4
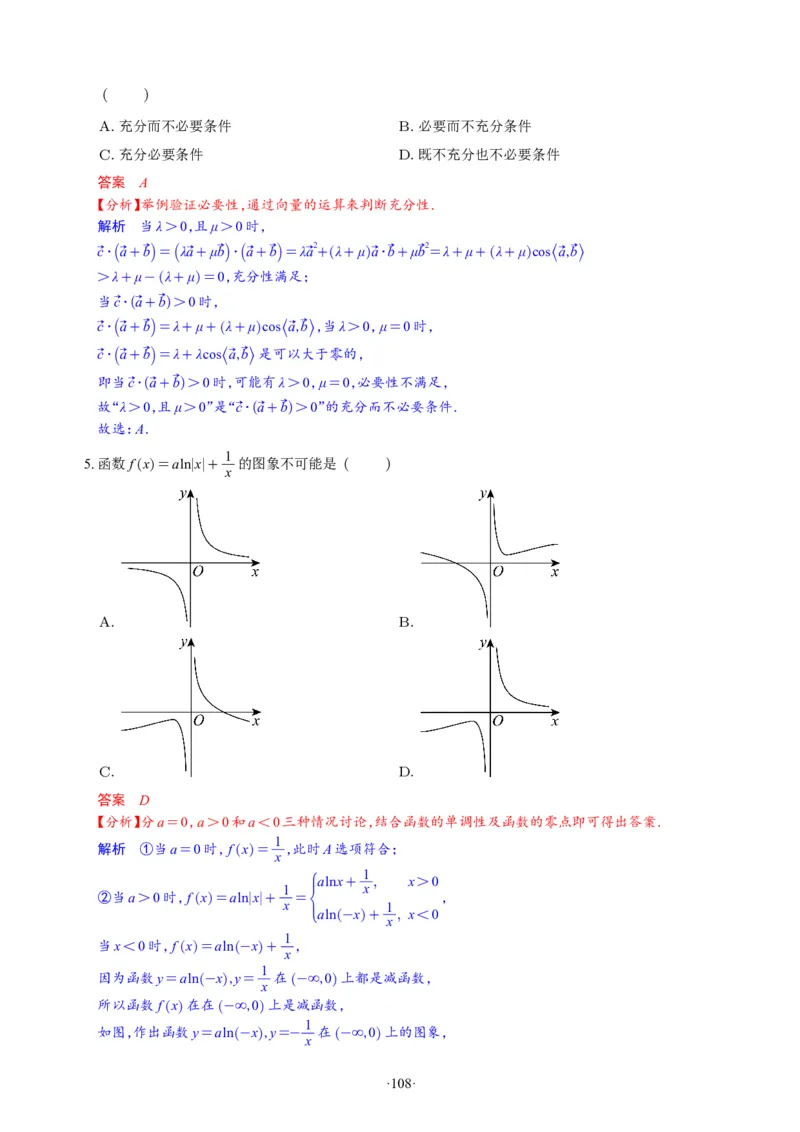
16.(15分)
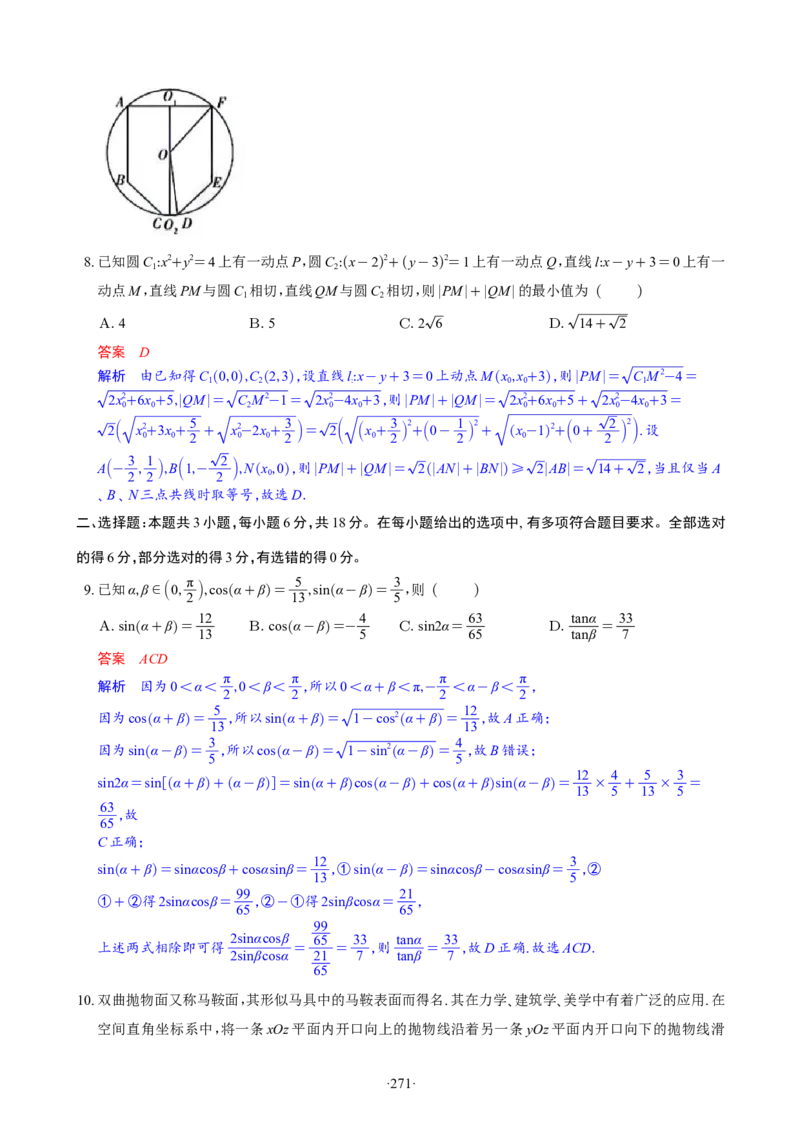
如图,在四棱锥P-ABCD中,底面ABCD是正方形,E,F分别为PB,PC的中点,G为线段AC上一点,且
CG=3AG.
(1)证明:EG∥平面BDF;
(2)若PD⊥平面ABCD,且AD=2PD,求二面角B-EG-D的正弦值.
解析 (1)记O为AC,BD的交点,连接CE交BF于点K,连接OK,
因为E,F分别为PB,PC的中点,则K为△BCP的重心,故CK=2EK.
CK OC
又因为四边形ABCD是正方形,故O为AC的中点,且由于3AG=CG,故OC=2OG, = =2,
EK OG
所以OK∥EG.
又因为OK⊂平面BDF,且EG⊄平面BDF,
所以EG∥平面BDF.
(2)以D为坐标原点,DA为x轴,DC为y轴,DP为z轴建立坐标系,
设AD =4,DP =2,则G3,1,0 ,B4,4,0 ,E2,2,1 ,
所以GB=1,3,0
,DG=3,1,0
,GE=-1,1,1 ,
·346·
平面BEG与平面DEG的法向量分别为m=x 1 ,y 1 ,z 1
,n=x 2 ,y 2 ,z 2 ,则
-
x 1 +
x 1 +
3y
y
1
1
=
+
0
z 1 =0
,
3
-
x
x
2
2
+
+
y
y
2
2
=
+
0
z 2 =0
,
不妨取x 1 =3,x 2 =1,则m=3,-1,4
,n=1,-3,4 ,
所以cosm,n
m⋅n
= m⋅ n
3+3+16 11
= = , 9+1+16× 1+9+16 13
11
所以二面角B-EG-D的正弦值为 1-
13
2 4 3
= .
13
17.(15分)
已知某客运轮渡最大载客质量为4000kg,且乘客的体重(单位:kg)服从正态分布N60,100 .
(1)记X为任意两名乘客中体重超过70kg的人数,求X的分布列及数学期望(所有结果均精确到0.001);
(2)设随机变量X ii=1,2,⋯,n 相互独立,且服从正态分布Nμ,σ2
n
X -nμ
i
,记ξ= i=1 ,则当n≥20时,
nσ
可认为ξ服从标准正态分布N0,1 .若保证该轮渡不超载的概率不低于97.7%,求最多可运载多少名乘
客.
附:若随机变量η服从正态分布Nμ,σ2 ,则P(μ-σ<η<μ+σ)=0.6826;若ξ服从标准正态分布
N0,1 ,则P(ξ<2)=0.977;0.15872≈0.0252,0.84132≈0.7078,0.1587×0.8413≈0.1335.
解析 (1)设乘客的体重为η,则η∼N60,100 ,其中μ=60,σ=10,
因为P(μ-σ<η<μ+σ)=0.6826,即P(50<η<70)=0.6826,
故P(η>70)=1-0.6826 ÷2=0.1587,
所以PX=0 =C0×0.84132≈0.708, 2
PX=1 =C1×0.1587×0.8413≈0.267, 2
PX=2 =C0×0.15872≈0.025, 2
所以X的分布列为:
X 0 1 2
P 0.708 0.267 0.025
方法1:所以EX ≈0×0.708+1×0.267+2×0.025=0.317.
方法2:因为X∼B2,0.1587 ,故EX =np≈0.317.
注:考生把≈写成=,不影响得分.
(2)设X i 为第ii=1,2,⋯ 位乘客的体重,则X∼Nμ,σ2 i ,其中μ=60,σ=10,
n
所以PX ≤4000
i
i=1
n
X -60n
i 4000-60n
=P i=1 ≤
10 n 10 n
≥0.977.
n
X -60n
i
4000-60n
因为 i=1 ~N(0,1).故有 ≥2,
10 n 10 n
得3n+ n-200≤0,即 n-8 3 n+25 ≤0,故 n≤8,n≤64,
所以若保证该轮渡不超载的概率不低于97.7%,最多可运载64名乘客.
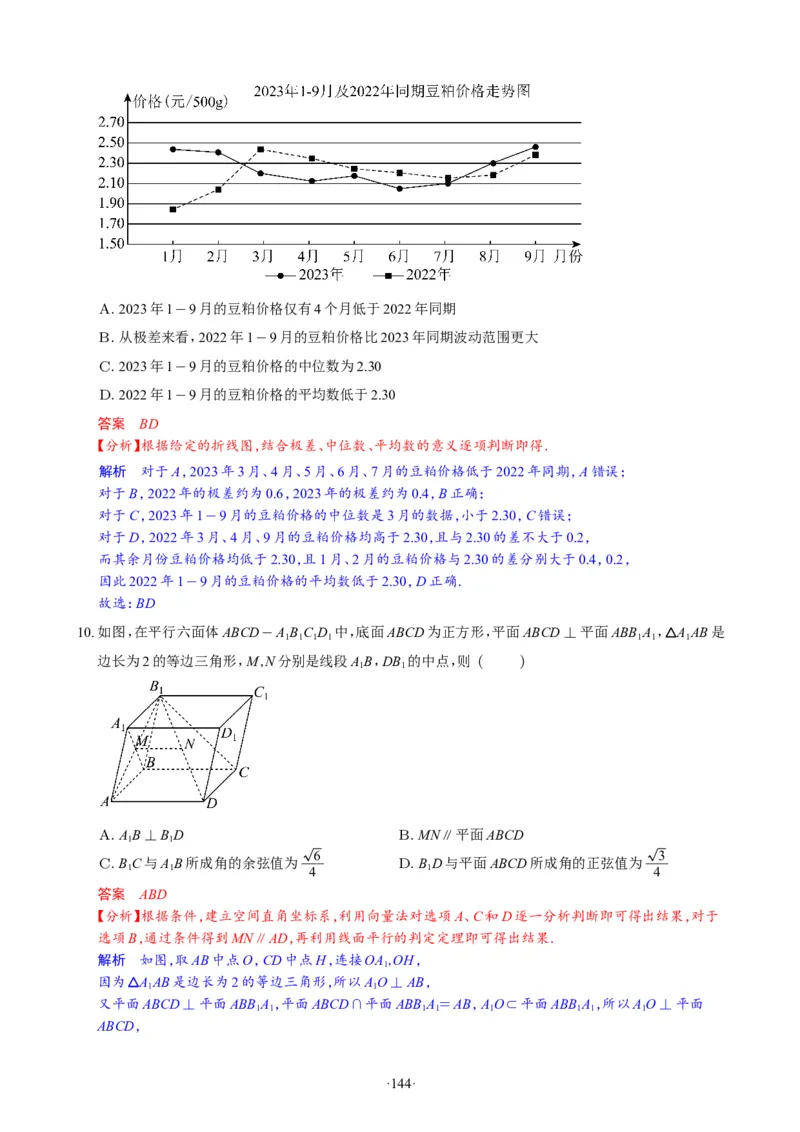
18.(17分)已知抛物线C:y2=4x的焦点为F,△PQR各顶点均在C上,且PF+QF+RF=0.
(1)证明:F是△PQR的重心;
·347·(2)△PQR能否是等边三角形?并说明理由;
21
(3)若P,Q均在第一象限,且直线PQ的斜率为 ,求△PQR面积.
3
解析 (1)设线段PQ的中点为M,由PF+QF+RF=0可知FP+FQ=2FM =RF,设QR的中点为N,
同理可知2FN=PF,
所以△PQR两条中线RM,PN相交于F,故F是△PQR的重心.
(2)方法1:根据题意有F1,0 .
设Px 1 ,y 1 ,Qx 2 ,y 2 ,Rx 3 ,y 3
,则PF=1-x 1 ,-y 1
,QF=1-x 2 ,-y 2
,RF=1-x 3 ,-y 3 ,
由PF+QF+RF=0可得,x +x +x =3,且y +y +y =0.
1 2 3 1 2 3
又由抛物线的几何性质可知PF =x 1 +1,QF =x 2 +1,RF =x +1. 3
若△PQR是等边三角形,则由(1)可知PF =QF =RF .
由PF =QF ,得x =x ,又因为P,Q不重合,故可知y =-y ≠0, 1 2 1 2
所以y 3 =-y 1 +y 2
3
=0,x =0,x =x = . 3 1 2 2
故PF =QF
5
=x 1 +1= 2 ,R0,0 ,RF =1,这与PF =QF =RF 矛盾.
综上,△PQR不可能是等边三角形.
方法2:根据题意有F1,0 .
设Px 1 ,y 1 ,Qx 2 ,y 2 ,Rx 3 ,y 3 ,由抛物线的几何性质可知PF =x 1 +1,QF =x 2 +1,RF =x +1. 3
若△PQR是等边三角形,则由(1)可知PF =QF =RF .
所以x +1=x +1=x +1,故x =x =x ,y2=y2=y2,
1 2 3 1 2 3 1 2 3
因此y ,y ,y 中至少两个相等,P,Q,R中至少有两个点重合,这与P,Q,R互不重合矛盾,故△PQR不可能
1 2 2
是等边三角形.
21
(3)方法1:设直线PQ的方程为y=kx+b,其中k= ,且因为P,Q在第一象限,
3
易知b>0,与C的方程联立有k2x2+2kb-2
x+b2=0,其中Δ>0,可知kb<1,
22-kb
结合(2)中所设点坐标可知x +x =
1 2
b2
,x x = .
k2 1 2 k2
由(2)可知x 3 =3-x 1 +x 2
3k2+2kb-4
= , k2
且y =-y -y =-2 x -2 x ,代入y2=4x 有:
3 1 2 1 2 3 3
x 1 +x 2 +2 x 1 x 2 =x 3 =3-x 1 +x 2
42-kb
,故
2b
+ -3=0, k2 k
8-3k2 1 8-3k2 21
整理化简有kb= = ,b= = ,
2 2 2k 14
PQ = 1+k2 x 1 -x 2
4 1+k2 1-kb k+b
= ,点F到直线PQ的距离d= k2
k+b
= , 1+k2 1+k2
dPQ
所以S =
△PQF
2k+b
=
2
1-kb 17 42
= .
k2 98
由(1)可知2FM =RF,故RM =3FM
51 42
,S =3S = . △PQR △PQF 98
21
方法2:由条件可设PQ的方程为y= x+b.把此方程与y2=4x联立,化简得7x2+2 21b-12
3
x+
3b2=0.
∴Δ=(2 21b-12)2-4×7×3b2=483- 21b
21
>0,∴b< .
7
12-2 21b
根据(2)有x 1 +x 2 = 7 ,∴x 3 =3-x 1 +x 2
9+2 21b
= , 7
·348·21
y 1 +y 2 = 3 x 1 +x 2
4 21
+2b= 7 ,∴y 3 =-y 1 +y 2
4 21
=- . 7
21
由y2=4x 解得b= .
3 3 14
12 21 21
∴x = ,直线PQ的方程为y= x+ .
3 7 3 14
∴PQ
21
= 1+ 3
2
x 1 -x 2
30 Δ 30 6 2
= ⋅ = × . 3 7 3 7
3 17 21
点R到直线PQ的距离d= × ,
30 14
1
所以△PQR的面积为 PQ
2
51 42
⋅d= .
98
19.(17分)
已知函数fx
x-b
=2aea -lnx-1.
(1)若a=-log 2 e,b=0,求fx 的极值;
(2)若a,b∈0,1 ,设x 1 =1,x n+1 =fx n .证明:
(i)x 0,gx
1
单调递增,当x> 时,g x
ln2
<0,gx 单调递减,
又因为g1 =g2 =0,故当00,fx
x
单调递增,当x>2时,f x
gx
=
<0,fx
x
单调递减.
故x=1是fx 的极小值点,fx 的极小值为f1
1
=- -1=-log e-1, ln2 2
x=2是fx 的极大值点,fx 的极大值为f2
1 1
=- -ln2-1=- log e-ln2-1. 2ln2 2 2
方法2:当a=-log 2 e,b=0时,fx
2 1
=- ⋅ ln2 2
x
-lnx-1,
所以f x 1 =
2
x-1 1 2x-2x - = .
x x⋅2x
设gx =2x-2x,则g x =2-2xln2在0,+∞ 单调递减.由于g 1 =21-ln2 >0,g 2 =
21-ln4 <0,故存在唯一x 0 ∈1,2 ,使得g x 0 =0.
当00,gx 单调递增;当x>x 0 时,g x <0,gx 单调递减.
因为g1 =g2 =f 1 =f 2 =0,所以当02时,gx <0,f x <0,fx
单调递减;当10,f x >0,fx 单调递增.
故x=1是fx 的极小值点,fx 的极小值为f1
1
=- -1=-log e-1, ln2 2
x=2是fx 的极大值点,fx 的极大值为f2
1 1
=- -ln2-1=- log e-ln2-1. 2ln2 2 2
(2)(i)设φx =fx
x-b
-λx=2ea -lnx-1-λx,
则当a>0时,φ x
x-b 1
=2ea - -λ在0,+∞
x
单调递增.
·349·令λ=1,当x∈1,+∞ 时,因为a,b∈0,1 ,故φ x ≥φ 1
1-b 1-1
=2ea -2>2ea -2>0,φx 单调递增,
故当x∈1,+∞ 时,φx ≥φ1 =2ae 1 a -b -2>2ae 1 a -1 -1 .
设hx =xe 1 x -1 -1,则h x 1 1 =1- ex-1,当02ha >2h1 =0.
所以x 1 =1,x 2 -x 1 =φx 1 >0,x 2 >x 1 =1;x 3 -x 2 =φx 2 >0,x 3 >x 2 >1;⋯;x n+1 -x n =φx n >0,x >x > n+1 n
1n=2,3,⋯ ,故对于任意n∈N*,x 0时,ex ≥ -1
x
+1,故ex≥x+1,当x=0时取等.故当x
∈1,+∞ 时,φ x ≥φ 1
1-b 1
=2ea -1-λ>2 -b+1
a
2
-1-λ= -2b+1
a
2
-λ,令λ= -2b+
a
1,则φ x >0,φx 在1,+∞ 单调递增.
由(i)可知1≤x n λx n+1 -x n ,x n+1 -x n ≥x 2 -x 1 λn-1=2ae 1 a -b -1 λn-1.
1-b 1
因为ea -1>a -b+1 a -1=a1-b ,故x n+1 -x n >2a1-b λn-1.
所以x n+2 -x n =x n+2 -x n+1 +x n+1 -x n >2a1-b λ+1 λn-1=4a1-b
1
-b+1 a λn-1,
且由a,b∈0,1 可知,4a1-b
1
-b+1
a
>41-b
2 1 1
>0,λ= -2b+1> ,λn-1≥ .
a a an-1
综上,有x n -x n+2 <4b-1
4b-1
λn-1≤
. an-1
·350·