文档内容
2024 学年第一学期丽水五校高中发展共同体期中联考
高二年级数学学科参考答案
命题:遂昌中学 彭志凯
龙泉中学 张傲伦
审稿:庆元中学 吴丽贞
1 2 3 4 5 6 7 8 9 10 11
D B D C A D A B BC BD ACD
1
12. y =− 13.
16
高二数学学科 试题 第1页(共4页)
6
5−1
14.
2
四.解答题(共5小题)
15.【解析】
4x+3y−2=0 x=2
解:(1)由 ,求得 ,
x+2y+2=0 y=-2
可得两直线l :4x+3y−2=0和l :x+2y+2=0的交点为
1 2
( 2 , - 2 ) ................3分
当直线 l 与直线3x+y−2=0平行,设 l 的方程为3x+ y+m=0,
把点(2,-2)代入求得 m = - 4 ,
可得l的方程为3x+y-4=0................6分
(2)当l的斜率不存在时,直线l的方程为 x = 2 ,满足点 A ( 4 ,1 ) 到直线l的距离为2....8分
当l的斜率存在时,设直限 l 的方程为y+2=k(x−2),即kx−y−2k−2=0,
则点A到直线 l
|4k−1−2k−2| 5
的距离为 =2,求得k = ,...11分
k2 +1 12
5 5
故l的方程为 x− y− −2=0,即5x−12y−34=0.
12 6
综上,直线l的方程为x=2或5x−12y−34=0................13分
16.【解析】
(1) 点D为BC的中点,
1
OD= (OB+OC),
2
2 1 2 1 1 2 1 1 2 1 1
2AE=EDOE= OA+ OD= OA+ (OB+OC)= OA+ OB+ OC = a+ b+ c .
3 3 3 3 2 3 6 6 3 6 6...7分
(2)
高二数学学科 试题 第2页(共4页)
A B = O B − O A ,由(1)得 O E A B = (
2
3
O A +
1
6
O B +
1
6
O C ) ( O B − O A )
=
1
2
O A O B +
1
6
O B
2
+
1
6
O C O B −
2
3
O A
2
−
1
6
O C O A
1 1 1 1 1 2 1 1
= 22 + 22+ 22 − 22 − 22 =−1.......15分
2 2 6 6 2 3 6 2
17.【解析】
(1)设圆的方程为x2 + y2 +Dx+Ey+F =0,可得
D
2
−
+
D
D
2
+
2
=
E
3 E
−
+
+
E
2
F
F
=
=
− 5
− 1 3 解得
D
E
F
=
=
=
−
−
7
4
4
圆的方程为 x 2 + y 2 − 4 x − 4 y + 7 = 0 ,即圆 C 的标准方程为 ( x − 2 ) 2 + ( y − 2 ) 2 = 1 ;......6分
(2)如图所示,圆(x−2)2 +(y−2)2 =1关于 x 轴的对称方程是 ( x − 2 ) 2 + ( y + 2 ) 2 = 1 ,
设m的方程为 y − 3 = k ( x + 3 ) ,即 k x − y + 3 k + 3 = 0 ,由于对称圆心 ( 2 , − 2 ) 到 m 的距离为圆的半径1,
则
| 2 k + 2
k
+
2
3
+
k
1
+ 3 |
= 1 ,
从而可得 k
1
= −
3
4
, k
2
= −
4
3
,故光线 m 所在直线的方程是 3 x + 4 y − 3 = 0 或 4 x + 3 y + 3 = 0 .....15分
18.【解析】
(1)设 P D 中点为 F ,连接EF, F C .
E,F 分别为PA,PD中点,
且 ,
且 ,
即四边形BCEF为平行四边形,
B E / / C F ,
EF //AD
又BE 平面PCD,CF 平面PCD
BE//平面PCD....5分
(2) 取AD中点记为O,连结PO,BO,
由等腰三角形PAD得:PO⊥ AD,
E F =
1
2
A D
EF //BC EF =BC高二数学学科 试题 第3页(共4页)
B O // C D , C D ⊥ A D , B O ⊥ A D ,且 P O B O = O ,
AD⊥平面POB,
PB平面POB P B ⊥ A D .....10分
(3)由(2)得,POB为平面PAD与平面ABCD所成二面角的平面角
,
设 A D = 4 , 则 P O = 2 , O B = 2 , P B = 2 3 则
,
P O B = 1 2 0 ,
即平面 P A D 与平面 A B C D 所成二面角的平面角为120
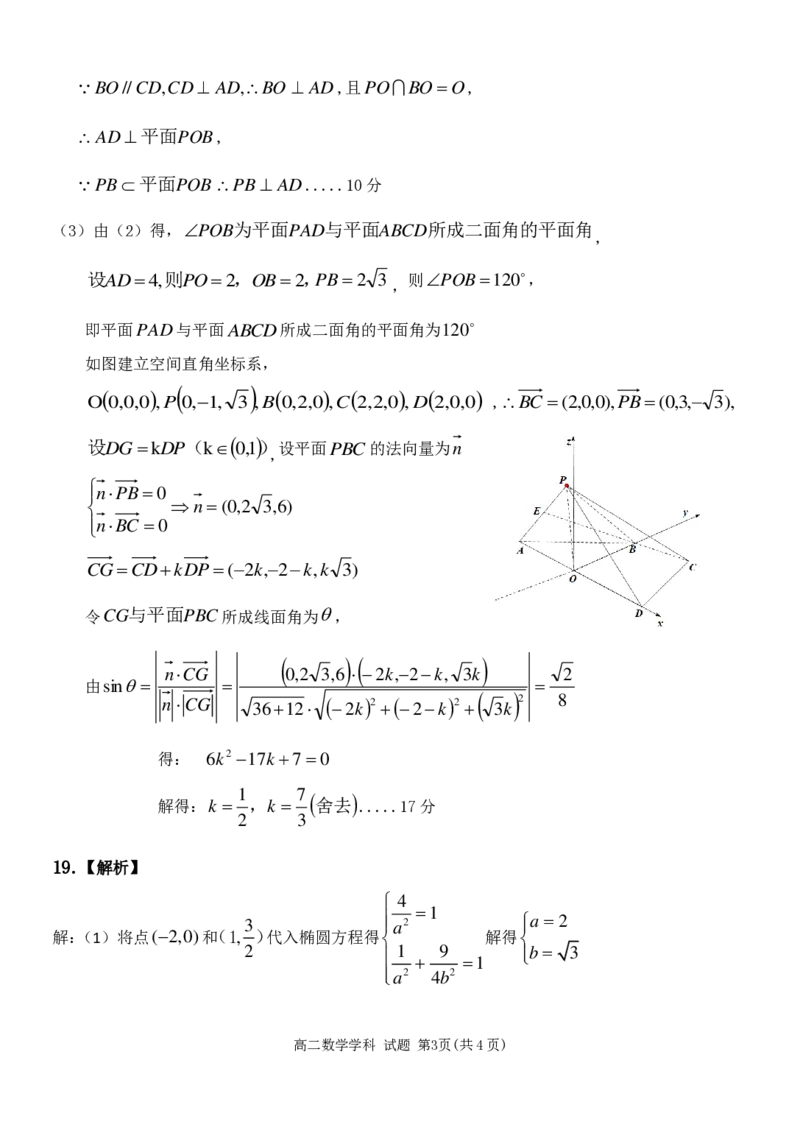
如图建立空间直角坐标系,
O
(
0 , 0 , 0
)
, P
(
0 , − 1 , 3
),
B
(
0 , 2 , 0
)
, C
(
2 , 2 , 0
)
, D
(
2 , 0 , 0
)
, B C = ( 2 ,0 ,0 ) , P B = ( 0 ,3 , − 3 ) ,
设 D G = k D P ( k ( 0 ,1 )) 设平面PBC的法向量为
,
n
n
n
P
B
B
C
=
=
0
0
n = ( 0 , 2 3 , 6 )
C G = C D + k D P = ( − 2 k , − 2 − k , k 3 )
令CG与平面PBC所成线面角为,
由 s in =
n
n
C
C
G
G
=
3 6 +
(0
1
,
2
2
3 ,6
( −
)
2
(
−
) k 2
2 k
+
,
(
−
−
2
2
−
−
k
k
,
) 2
3
+
k
)(
3 k )2
=
8
2
得: 6 k 2 − 1 7 k + 7 = 0
解得: k =
1
2
, k =
7
3
(
舍 去
)
.....17分
19.【解析】
解:(1)将点 ( − 2 , 0 )
4
=1
3 a2 a = 2
和(1, )代入椭圆方程得 解得
2
1 9 b = 3
+ =1
a2 4b2则椭圆
高二数学学科 试题 第4页(共4页)
C 的标准方程为
x
4
2
+
y
3
2
= 1 ;....4分
(2)△PBF 周长
1
L 为 4 a = 8 ,....5分
面积 S
P B F 1
=
1
2
F
1
F
2
y
P
− y
B
= y
P
− y
B
,....6分
设 P B 所在直线方程为 x = n y + 1 ,与椭圆方程
x
4
2
+
y
3
2
= 1 联立得
( 3 n 2 + 4 ) y 2 + 6 n y − 9 = 0
y
y
P
P
+
y
y
B
B
=
=
−
−
3
3
n
6 n
2 n +
9
2 + 4
4
y
P
− y
B
=
=
=
1
3
2
3
( y
n
n
P
n
2
2
+
2
+
+
+
4
1
y
B
1
1 2
+
) 2 −
n
4
1
2
y
+
P
1
y
B
....8分
令 t = n 2 + 1 1
S
P B F 1
=
3
1
t
2
+
1
t
3 ( t = 1 时取最大值),即△ P B F
1
9
内切圆面积的最大值为 .....10分
16
(3)证明:设 P ( x
0
,y ),
0
A ( x
1
,y ),
1
B ( x
2
, y
2
) ,
因为点 P 在椭圆上,
x2 y2
所以 0 + 0 =1,
4 3
即3x2 +4y2 =12.
0 0
由(1)得F(−1,0),F (1,0),
1 2设直线
高二数学学科 试题 第5页(共4页)
P A 的方程为x=my−1, m =
x
0y
+
0
1
,
x=my−1
联立x2 y2 ,消去x并整理得
+ =1
4 3
( 3 m 2 + 4 ) y 2 − 6 m y − 9 = 0 ,
此时△ 0 ,
由韦达定理得 y
0
y
1
=
3 m
−
2
9
+ 4
=
3 (
x
0y
−
+
0
9
1
) 2 + 4
,
同理得 y
0
y
2
=
3 (
x
0y
−
−
0
9
1
) 2 + 4
,
所以
S
3
S
−
2
S
2
+
S
2
S 1−
S
1
= S
S
P
A
F B1
F B1
+ S
S
P
B
F F1
F F1
2
2
=
1
21
2
|
|
P
A
F
F
1
1
|
|
|
|
F
F
1
1
B
B
|
|
s
s
in
in
P
A
F
F
1
1
B
B
+
1
21
2
|
|
P
B
F
F
2
2
|
|
|
|
F
F
1
1
F
F
2
2
|
|
s
s
in
in
P
B
F
F
2
2
F
F
1
1
=
|
|
P
A
F
F
1
1
|
|
+
|
|
P
B
F
F
2
2
|
|
=
−
y
0y
1
+
−
y
0y
2
= − y
0
(
1
y
1
+
1
y
2
) ....14分
=
y 20 [ 3 (
x
0y
+
0
1
) 2 + 4
9
+ 3 (
x
0y
−
0
1
) 2 + 4 ]
=
3 ( x
0
+ 1 ) 2 + 3 (
9
x
0
− 1 ) 2 + 8 y 20
=
6 x 20 + 8
9
y 20 + 6
=
2 4 +
9
6
=
1 0
3
.
故
S
3
S
−
2
S
2
+
S
2
S
1−
S
1
为定值. ....17分