数学答案_2024-2025高二（7-7月题库）_2024年12月试卷_1227四川省绵阳市南山中学2024-2025学年高二上学期12月月考_四川省绵阳市南山中学2024-2025学年高二上学期12月月考数学试题PDF版含答案

绵阳南山中学 2024 年春季高 2023 级 12 月月考
数学试题参考答案
一、选择题
题 号 1 2 3 4 5 6 7 8 9 10 11
选 项 B B B A C D B D ABD BCD AB
二、填空题
12. ， 13. 14.
1 6 8
三、解0答
2
题
4 2 81
15.（1）设“甲胜且编号的和为6”为事件A．
甲编号为x，乙编号为y，x,y表示一个基本事件，
则两人摸球结果包括
(
1,2
),(
1,3
),(
1,5
),,(
2,1
),(
2,2
),(
5,4
),(
5,5
)
共25个基本事件；
A包括的基本事件有1,5,2,4,3,3,4,2,5,1共5个．
花
5 1 1
∴P(A)  ．甲胜且编号的和为6的事件发生的概和率为 ．
25 5 5
儿
（2）这种游戏不公平． 云
：
设“甲胜”为事件B，“乙胜”为事件C号 ．甲胜即两个编号的和为偶数所包含基本事件数为以下
众
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
13个： 1,1 , 1,3 , 1,5 , 公2,2 , 2,4 , 3,1 , 3,3 , 3,5 , 4,2 , 4,4 , 5,1 , 5,3 , 5,5 ．
13 13 12
所以甲胜的概率为P(B) ， 乙胜的概率为P(C)1  ，
25 25 25
∵P(B) P(C)，∴这种游戏规则不公平．
16.（1）圆C:x2y52 9的圆心C0,5，半径为3，
设圆C 的圆心坐标为a,b，半径为r，
1
a12


b 3
2
r2
 a0
 
所以a2b22 r2 ，解得b0，
 
a2b52 r32 r2

所以圆C 的方程为x2y2 4.
1
（2）若直线l斜率不存在，此时l：x1，
x1
 ，解得y 3，
x2 y2 4
第 1 页 共 6 页 
此时弦长为 3  3 2 3 ，符合题意，
若直线l直线斜率存在，设l：y2kx1，
因为弦长为2 3，所以圆心C 0,0到直线l的距离d  r2  3 2 1，
1
k2 3
因为l:kxyk20，所以d  1，解得k  ，
k21 4
3
所以直线l的方程为y2 x1，即3x4y50，
4
综上：直线l的方程为x1或3x4y50.
17.（1）由频率分布直方图可得100.0100.0152a0.0250.0051，解得a0.030.
70,80的频率为10a0.3， 80,90的频率为100.0250.25，
90,100的频率为100.0050.05，按分层抽样方法抽取12人的成绩，
花
0.05
则12人中成绩不低于90分的人数为12
和
1.
0.30.250.05
儿
（2）该校学生首轮数学竞赛成绩的平均数为云：
：
10450.010550.015650.01号5750.030850.025950.00571.
众
 40,70的频率为100.01 公 00.0150.0150.4，
 40,80的频率为0.4100.0300.7 ，
设中位数为x,则x 70,80，
则0.40.030x700.5，解得x73.33，
故该校学生首轮数学竞赛成绩的平均数约为71分，中位数约为73.33分.
（3）设A“至少有一位同学复赛获一等奖”，
则PA1P  A  1  1 3   1 2  13 ,
 5  3 15
13
故至少有一位同学复赛获一等奖的概率为 .
15
18.（1）取BD中点O，连接PO，
1
P是BM的中点，PO//MD，且PO MD，
2
在线段CD上取点F ，使DF 3FC，连接OF，QF，
第 2 页 共 6 页1 1
，QF //AD，且QF  AD MD ，
4 2
AQ P = O/ 3 / Q Q C F,POQF ，四边形POFQ为平行四边形，PQ//OF，
又PQ平面BCD,OF 平面BCD，PQ//平面BCD.
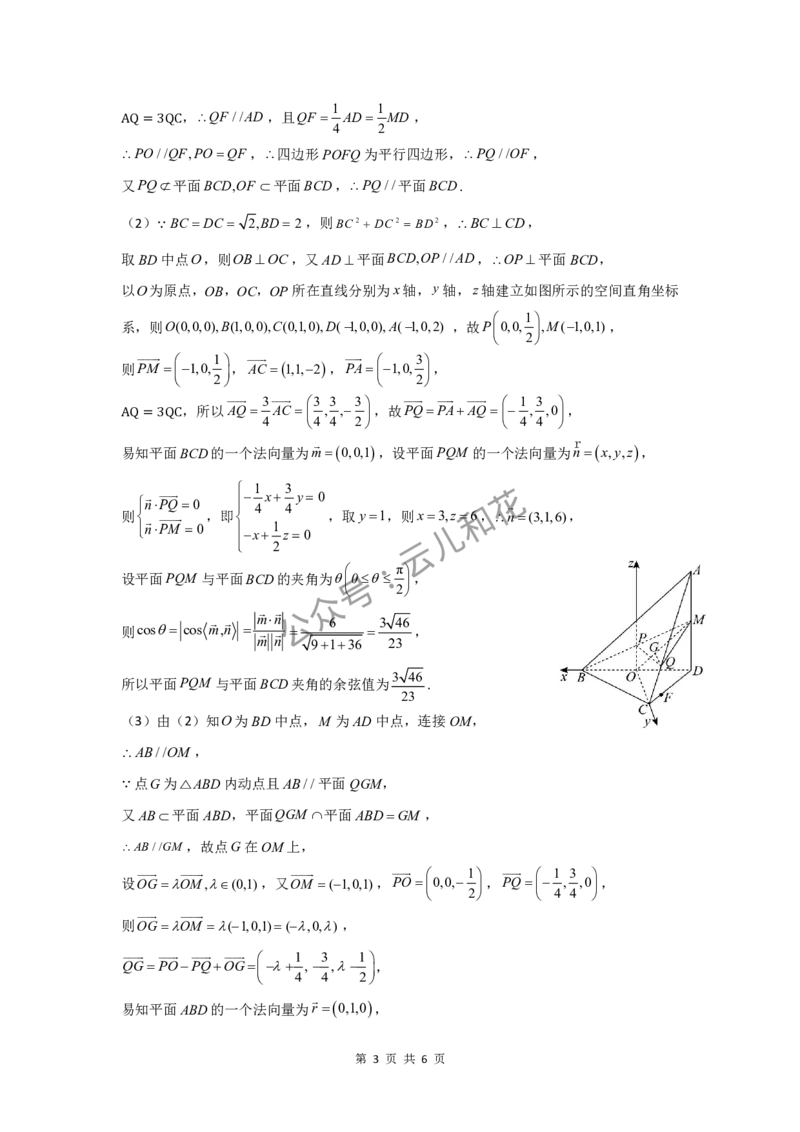
（2）BC DC  2,BD 2，则BC2  DC2  BD2，BCCD，
取BD中点O，则OBOC，又AD平面BCD,OP//AD，OP平面BCD，
以O为原点，OB，OC，OP所在直线分别为x轴，y轴，z轴建立如图所示的空间直角坐标
 1
系，则O(0,0,0),B(1,0,0),C(0,1,0),D(1,0,0),A(1,0,2) ，故P0,0, ,M(1,0,1)，
 2
  1    3
则PM 1,0, ，AC 1,1,2，PA1,0, ，
 2  2
 3 3 3 3     1 3 
，所以AQ AC  , , ，故PQPAAQ  , ,0，
4 4 4 2  4 4 
A 易 Q 知 = 平 3 面 QC BCD的一个法向量为m  0,0,1，设平面PQM 的一个法向量为n r x,y,z，
    1 x 3 y 0 花
 nPQ0   4 4 和 
则   ，即 ，取y1，则x3,z6，n(3,1,6)，
nPM 0 x 1 z 0 儿
 2 云
：
 π
设平面PQM 与平面BCD的夹角为号0 ，
 2
众
 公
  mn 6 3 46
则cos cos m,n      ，
m n 9136 23
3 46
所以平面PQM 与平面BCD夹角的余弦值为 .
23
（3）由（2）知O为BD中点，M 为AD中点，连接OM，
AB//OM ，
点G为△ABD内动点且AB//平面QGM，
又AB平面ABD，平面QGM 平面ABDGM ，
AB//GM ，故点G在OM上，
     1   1 3 
设OG OM,(0,1)，又OM (1,0,1)，PO0,0, ，PQ , ,0，
 2  4 4 
 
则OG OM (1,0,1) (,0,) ，
     1 3 1
QG POPQOG ,  , ，
 4 4 2

易知平面ABD的一个法向量为r 0,1,0，
第 3 页 共 6 页 π
设QG与平面ABD所成角为0 ，则最大时，sin最大，
 2
  3
  QGr 4
sin cos QG,r    
QG r  1 2 3 2  1 2
     
 4 4  2
3 3
4 4
  , (0,1)
，
22 3  7 2   3  2  19
2 8  8 32
3
所以当 时，sin最大，此时最大，即当点G位于△ABD中位线OM 靠近O的八等分
8
点的第3个点处时，QG与平面ABD所成角最大.
19.由题意可知，“特征三角形”是等腰三角形，且腰长为a，底边长为2c，
那么相似比就是两个“特征三角形”的长半轴长之比或者是焦距之比，
从而特征三角形相似的两椭圆的离心率是相等的.
由椭圆 x2  y2 1的离心率为e 2 ， 花
2 2 和
  x2 儿 2
可知过点 2, 2 ，且与椭圆  y2 1相似的椭圆方程的离心率也为e ，
云
2 2
：
x2 y2   4 2
可设所求椭圆为  1，代点 号2, 2 得：   1，
a2 b2 a2 b2
众
b2 a2c2 公1 1
再由  1e2 1  ，所以a2 2b2，
a2 a2 2 2
x2 y2
联立上两式解得：a2 8,b2 4，所以所求椭圆方程为：  1.
8 4
（2）①由椭圆C 与椭圆C 的相似比为
3
，可知两椭圆的长半轴之比也为
3
，短半轴之比
2 1
x2 y2 x2 y2
也为 3 ，再由椭圆C :  1，所以椭圆C :  1，
1 4 3 2 12 9
x2 y2
当直线m的斜率不存在时，又与椭圆C :  1相切，则切线方程为x2，
1 4 3
x2 y2    
取直线x2，可得与椭圆C :  1的交点坐标为A 2, 6 ,B 2, 6 ,
2 12 9
此时有 AB 2 6，
再当直线m的斜率存在时，可设直线m的方程为y kxn，
则与椭圆C :
x2

y2
1联立消y得：3x24kxn2 12，
1 4 3
整理得：  34k2 x28knx4n2120，
第 4 页 共 6 页由直线m与椭圆C 相切，可得：8kn24  34k2 4n212  0，整理得n2 34k2，
1
再由直线m的方程为y kxn，与椭圆C :
x2

y2
1联立消y得：3x24kxn2 36，
2 12 9
整理得  34k2 x28knx4n2360，
由8kn24  34k2 4n236  48  n2912k2 ，
再把n2 34k2代入得：48
 34k2912k2
96
 34k2
0，
8kn 4n236
可设交点Ax
1
,y
1
,Bx
2
,y
2
，则有 x 1 x 2  34k2 , x 1 x 2  3 4k2 ，
所以 AB  1k2 x x  1k2 x x 24x x
1 2 1 2 1 2
 8kn  2 4n2 36 3n2 2736 k2
 1k2   4 4 1k 2
34k2  3 4k2  34k22
912k22736k花2 18 24k 2
再把n2 34k2代入得： AB 4 1k2
 34k2和2
4 1 k2
 34k22
儿
云
1 34k2

1
：
1k2 4 4 1 ，
4 6 4 6 号2 6 1
34k2 34k2 34k2
众
公
1  1 
由于k2 0，所以
34k2


0,
3  
，即 AB  2 6,4 2

，
综上可得： AB 2 6,4 2；
 
②假设直线l存在；
当l的斜率不存在时，l:x1，
x1 x1
x1  x1 
由 解得 3，由 解得
33
，
3x24y2 12 y 3x24y2 36 y
 2  2
 33  33  3  3
所以P

1, 

,S

1, 

,Q1, ,R1, ，
 2   2   2  2

 
  333   333
所以PS  0, 33 ,RS 0, ,QS 0, ，
   
 2   2 
     333     7 3321
所以5PS2RS 5 0, 33 20,  0,6 333 ,7QS 0, ，
   
 2   2 
第 5 页 共 6 页  
显然5PS2RS 7QS ；
当l的斜率存在时，l:ykx1k0，设Qx,y ,Rx ,y ,Px ,y ,Sx ,y ，
1 1 2 2 3 3 4 4
ykx1
联立 ，可得  34k2 x28k2x4k2120，
3x24y2 12
8k2 4k212
所以x x  , xx  ，
1 2 34k2 1 2 34k2
ykx1
联立 ，可得  34k2 x28k2x4k2360，
3x24y2 36
8k2 4k236
所以x x  , x x  ，
3 4 34k2 3 4 34k2
x x x x 4k2
所以 1 2  3 4  ，即QR,PS中点的横坐标相同，
2 2 34k2
又因为P,Q,R,S四点共线，所以QR的中点即为PS的中点，
   PS  QR PS  QR
因为5PS2RS 7QS，所以5 PS 2 7 ，
花
2 2
和
所以5 PS 9QR ， 儿
云
：  8k2  2 4k212
因为 QR  1k2  x x2 4xx号 1k2     4 
1 2
众
1 2

34k2
 
34k2

公
144144k2 12
 1k2
 1k2   ，
 34k22 34k2
 8k2  2 4k2 36
PS  1k2 x x 24x x  1k2  4  
3 4 3 4

34k2
 
34k2

432528k2 4
 1k2 2733k2
 1k2   ，
 34k22 34k2
4
 1k2 2733k2
12
 1k2
所以 ，
5 9
34k2 34k2
3
所以 5 2733k2 27 1k2 5 911k2 9 33k2 ，解得k  ，符合条件，
4
所以存在直线l:3x4y30满足条件.
第 6 页 共 6 页