数学答案_2024-2025高二（7-7月题库）_2025年01月试卷_0103湖北省腾云联盟2024-2025学年高二上学期12月联考_湖北省腾云联盟2024-2025学年高二上学期12月联考数学试卷（PDF版，含答案）

参考答案：
一单选题：
1 2 3 4 5 6 7 8
C B A C D D A B
二．多项选择题：
9 10 11
BCD ABD ACD
三填空题：
12.25 13. 14.-1
2 65
四解答题： 5
     
15.【解析】（1）记ABa,ADb,AA c，
1
因为平行六面体ABCDABCD 的各条棱长均为2，
1 1 1 1
AABAADBAD60，
1 1
r r r
     
所以 a  b  c 2，abacbc 22cos60 2 ，.............................................2
...................................................................................................................4
3
1  =  −5   −  
..............................................................................................6
3 2 2 34
（   2 1   ）  记=  A  B  (   − a  , 5  A    D  −     b  ) ,  A  = A  5 c  ，
1
因为平行六面体ABCDABCD 的各条棱长均为2，
1 1 1 1
AABAADBAD60，
1 1
r r r
     
所以 a  b  c 2，abacbc 22cos60 2 ，
         
因为AC  ABBCCC  ABADAA abc，
1 1 1
         
AB ABAA ac, BD ADABba，..................................................8
1 1
所以
                
    2 2
AC AB abc  ac a abacacbcc 4222240，.........11
1 1
 
同理AC BD0，则AC  AB,AC BD，
1 1 1 1
又ABBDB,AB,BD平面ABD，所以AC 平面ABD..........................13
1 1 1 1 1
16 （1）首先根据圆的弦长公式设圆心到直线距离为d,
可得 ,所以 ...........................................................................2
2 2
若直线
M
斜
N
率
=
不
2
存
R
在
−
时
d
，
=
直
2
线方
30
程为x=d2= 此时
6
d=2不满足题意。.................................................3
{#{QQABaQQAggCIAAIAABgCEwUCCEGQkhAAASgOBAAIsAAByBFABAA=}#}所以直线斜率存在，设直线方程为y-3=k(x-2)
圆心到直线距离为 ,
2−2k
所以即得直线斜率d= k 2 +1= ...6...............................................................................................6
所学直线方程为 k=−2± 3 或 .........................7
(2)设圆心到直线 yA=B( 的 − 距 2 离 + 为 3)x ， + 圆 7 心 − 到 2 直 3 线CyD= 的 (− 距 2 离 − 为 3),x+7+2 3
.................  ..1.................................................  ..2.................................10
2 2 2
1 +  2 =   =,8 ............................................................................12
2 2
四   边形=2ABC3D6的−面  1积为   =2 36−  2
1 2 2 2 2
又因为 S=     ，=“2 =(”36成−立  当1 且)(3仅6当−  2 )=时2 ，36即−36×8+(  1  2)
2
所以 2 ；...2......................................................................................................................15
1 +  2 ≥2  1  2  1 =  2  1  2 ≤4
(没验证等号成立的条件扣1分)
≤ 64
17.(1)首先F(1,0),得c=1，设A( ),B( )..........................................................................1
当直线l过F时，直线方程  1为,  1：  2,  2 .......................................................2
3
y= 3 (x−1)
与椭圆联立方程： 得
3
y= 3 (x−1)
2 2

2 2
+  =1
2 2 2 2 2 2 2
,且 (a +3b，).x.....−...2...a...x...+....a....−....3..a....b.....=....0...........................5
2
2a 4 2 2
解1得+  2 =a 2 +3b 2 =13 a −b =1
所以椭a圆=方2,b程=为：3 ...........................................................................6
2 2

（2）M(-2,0)设直线4l+方3程=为1 ,A( ),B( )
y+ 3=k(x+2)  1,  1  2,  2
与椭圆联立方程： 得
y+ 3=k(x+2)
2 2

4 + 3 =1
2 2 2 2
(3+4k )x +(16k −8..3...k..).x...+....1..6..k.....−....1..6.....3..k...=....0...................9
2 2
−16k +8 3k 16k −16 3k
∆>0,  1+  2 = 3+4k 2 ,  1  2 = 3+4k 2
..................12
1  2 1 1  1+  2+4
1+  2 =  1+2+  2+2 =2  − 3(  1+2+  2+2)=2  − 3  1  2+2(  1+  2)+4
将韦达定理代入计算，即得 −16k2+8 3k ............15
3+4k2 +4
1+  2 =2  − 316k2−16 3k −16k2+8 3k =− 3
3+4k2 +2( 3+4k2 )+4
{#{QQABaQQAggCIAAIAABgCEwUCCEGQkhAAASgOBAAIsAAByBFABAA=}#}18（1）根据题目意思，在四棱锥 中，有 // ,因为 平面 , 平面 ，
⧸
所以 //平面 ，  −           ⊂      ⊂   
又因为   平  面   且平面 平面 = ，所以 // ，
又因为   ⊂平面    , 平  面   ∩ ，       
⧸
所以 //  平  面⊂  ..  ..  ...  ....  ..⊂...........  ..  ..  ...  ...............................................................................4
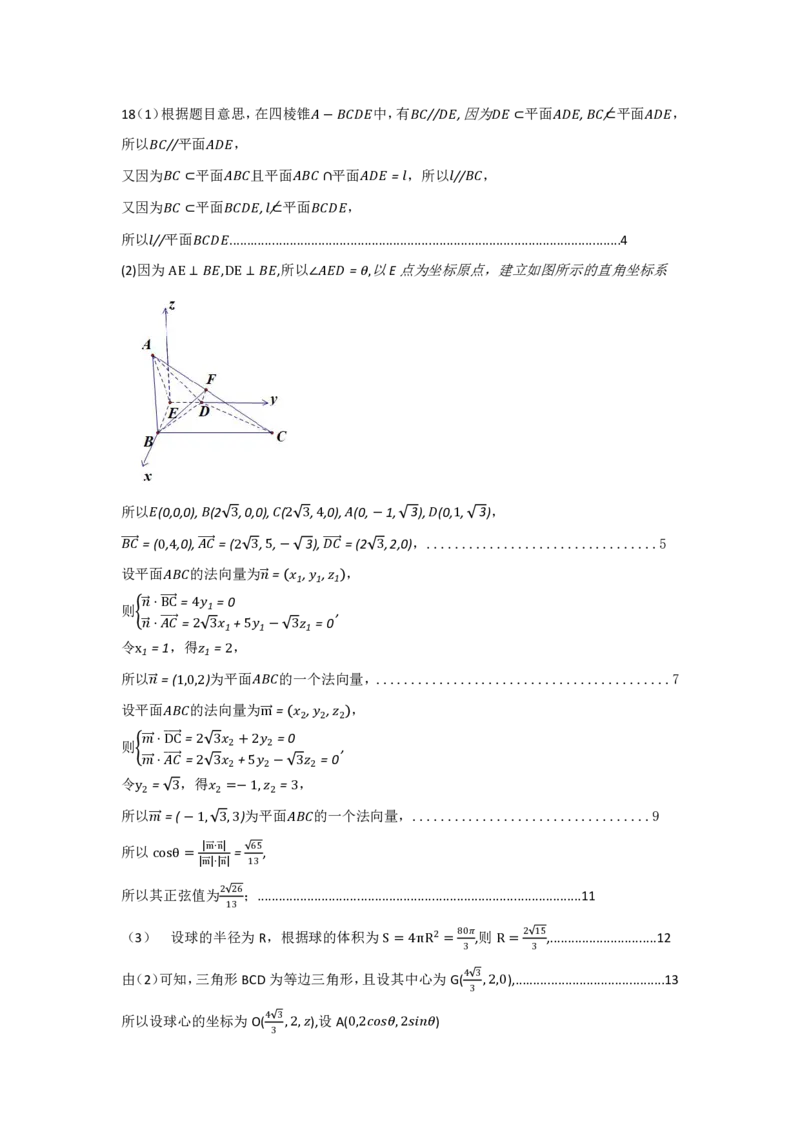
(2)因  为     , ,所以 = 以E点为坐标原点，建立如图所示的直角坐标系
AE⊥   DE⊥   ∠     ,
所以 (0,0,0), (2 ,0,0), ( , ,0), (0, 1, 3), (0, , 3)，
=  ( , ,0),  =(3 ,  , 2 33)4,  =(2 −,2,0)，.  ...1.............................5
  设  平面04 的  法  向量2 为3 5=− , ,     ， 3
1 1 1
则   =  1 =0       ,
= + =0
  ⋅BC 4  1 1 1
令 1   = ⋅  1  ，  得 2 13 =  ， 5  − 3 
所以x =(  )为平2 面 的一个法向量，..........................................7
设平面   1,0的,2法向量为    = , , ，
则
= m =0  2  2  2
,
= + =0
⋅DC 2 3  2+2  2
令   = ⋅     ，得 2 3  2 5  2− = 3 ，  2
所以y2 =3(  2 =−)为1,平  2面 3 的一个法向量，..................................9
所以   −1, 3,3 = ,   
|m⋅n| 65
cosθ=|m|⋅|n| 13
所以其正弦值为 ；...........................................................................................11
2 26
13
（3） 设球的半径为R，根据球的体积为 ,则 ,..............................12
2 80  2 15
S=4πR = 3 R= 3
由（2）可知，三角形BCD为等边三角形，且设其中心为G( ),..........................................13
4 3
3 ,2,0
所以设球心的坐标为O( ),设A( )
4 3
3 ,2,  0,2     ,2    
{#{QQABaQQAggCIAAIAABgCEwUCCEGQkhAAASgOBAAIsAAByBFABAA=}#}2 15
=   =
即： , 3 ...........................................16
2 3 16 2 2 3 2 20
z= 3 3 +(2−2     ) +( 3 −2     ) = 3
解方程即得 ................................................................................................................17
π
θ= 3
19.(1)①根据椭圆的光学性质，若经过左顶点反射，路程为 ,则 ；
1
2(a−c)=6c e= 4
若经过右顶点反射，路程为2(a+c)=6c，则 ；
1
e= 2
若经过的反射点不过左右顶点时，路程为4a=6c，则 ；
2
e= 3
所以椭圆的离心率可以为 ， ， ..................................................3
1 1 2
②设Q(4,t)( ), 4 2 3 ,
t≠0 M(x1,y1),N(x2,y2)
根据题目已知条件可知椭圆方程为 .......................................................................4
2
2
4 +  =1
则 , ,
6 2
QA1:x= ty−2QA2:x= ty+2
分别与椭圆联立： 6 得到 ................................................................5
x= ty−2 6 
2 2  1 =  2 +9
4 +  =1
2 得到 ..............................................................6
x= ty+2 −2 
2 2  2 =  2 +1
4 +  =1
...................................................8
1
1 2   1   2       1   2  2 (  2 +9)(  2 +1)
1 2 2
令2 = 2         =     =(  −  1)(  −  2)= (  +3)
2
则m= t +3>3
,
1 (  +6)(  −2) 1 2 1 1 1
2
2 =  =−12(  ) +4  +1,(0<  <3)
当且仅当 ,即m=6， 时， 取最大值 ..............................................10
1 1 1  1 4
（2）设直  线 = M 6∈ N ( 的 0, 方3) 程为 t=± 3  2 3
根据双曲线的光学性质可知x=my+的5内心为I为 与 的交点，
∆M  1     
联立  1   1  消去y得到 .................................................................................11
9 − 16 =1 9(y2−y1)
2   2  x= x1y2−x2y1
9 − 16 =1
又因为 代入计算即得 ......................................................13
9
下证 x1 =m 的 y 内 1+ 心 5 在 ,x 直 2 = 线 m x y = 1 3 + 上 5 ， x= 5
∆M  1  2
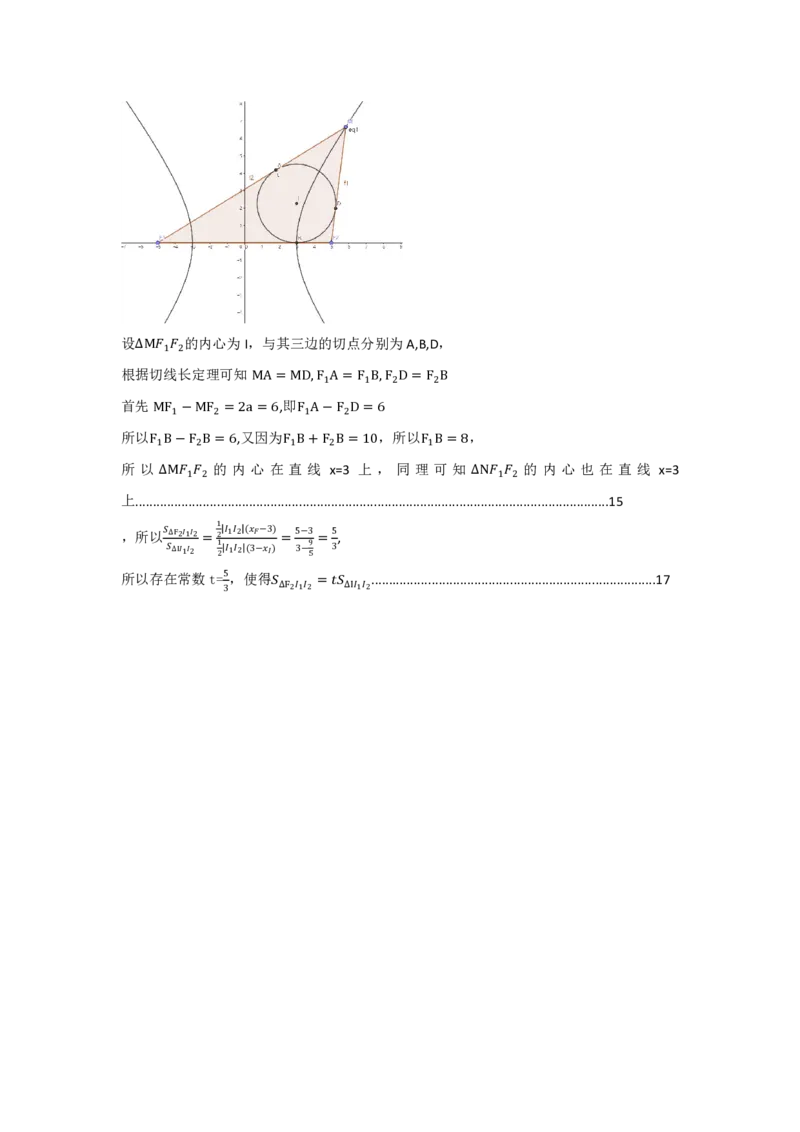
{#{QQABaQQAggCIAAIAABgCEwUCCEGQkhAAASgOBAAIsAAByBFABAA=}#}设 的内心为I，与其三边的切点分别为A,B,D，
根据∆M切  线1  长2 定理可知
首先 MA=,即MD,F1A= F1B,F2D= F2B
所以MF1−MF2 =,2又a因=为6 F1A−F2D= 6，所以 ，
所 以F1B−F2B的=6内 心 在F直1B线+F2 x=B3=上10， 同 理F1可B=知8 的 内 心 也 在 直 线 x=3
上.......∆...M...  .. 1 ..  .. 2 ............................................................................∆..N...  .. 1 ..  .. 2 ...........................15
，所以 ,
1
∆F2  1  2 2  1  2(   −3) 5−3 5
1 9
∆I  1  2 = 2  1  2(3−   ) = 3−5 =3
所以存在常数t= ，使得 ................................................................................17
5
3  ∆F2  1  2 =   ∆I  1  2
{#{QQABaQQAggCIAAIAABgCEwUCCEGQkhAAASgOBAAIsAAByBFABAA=}#}