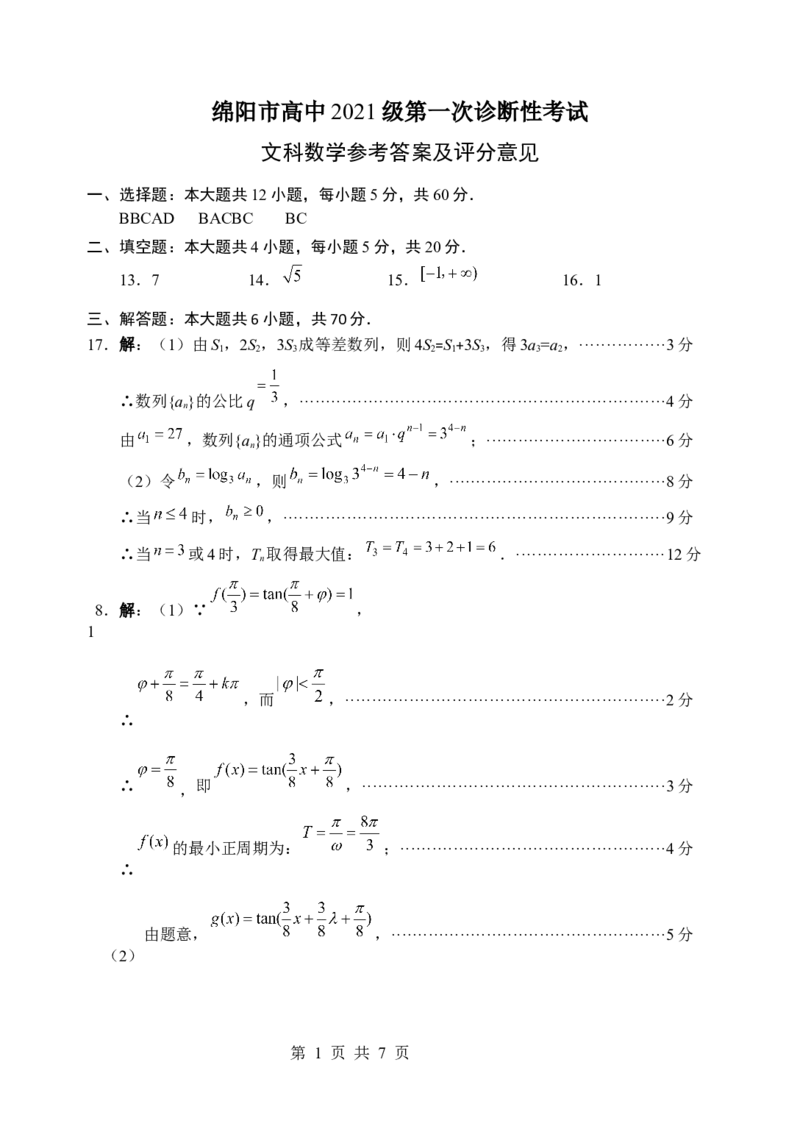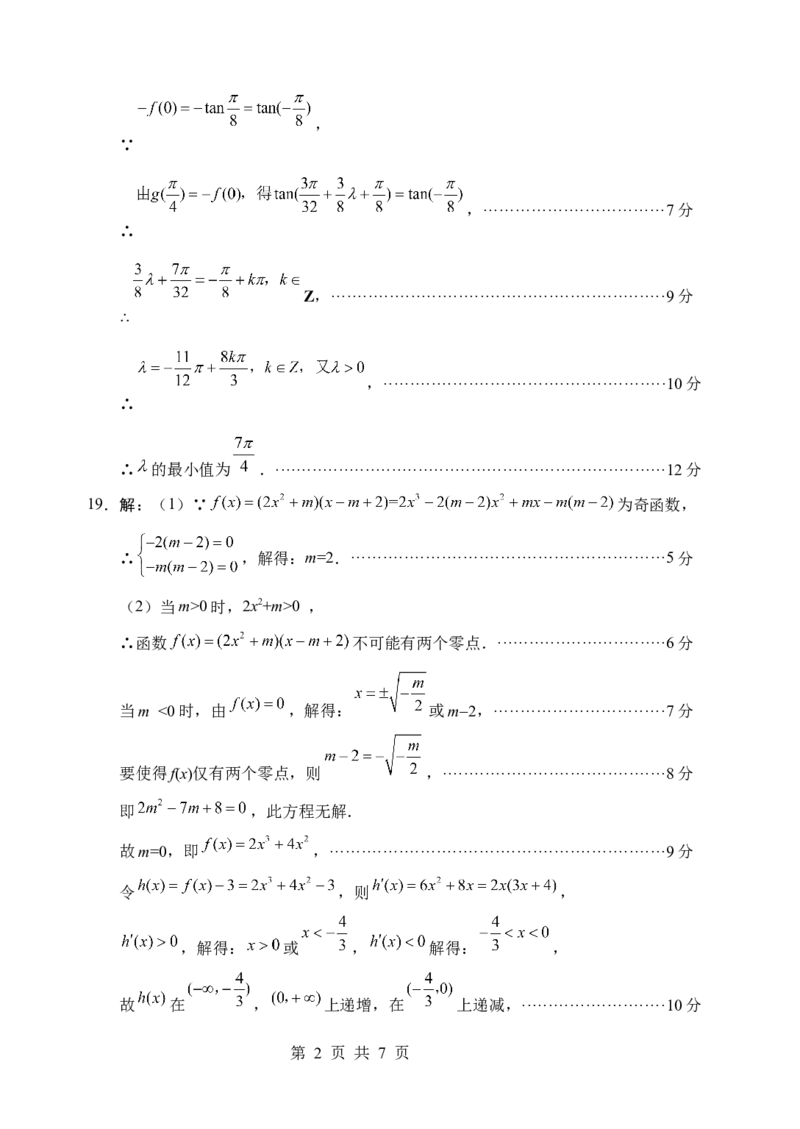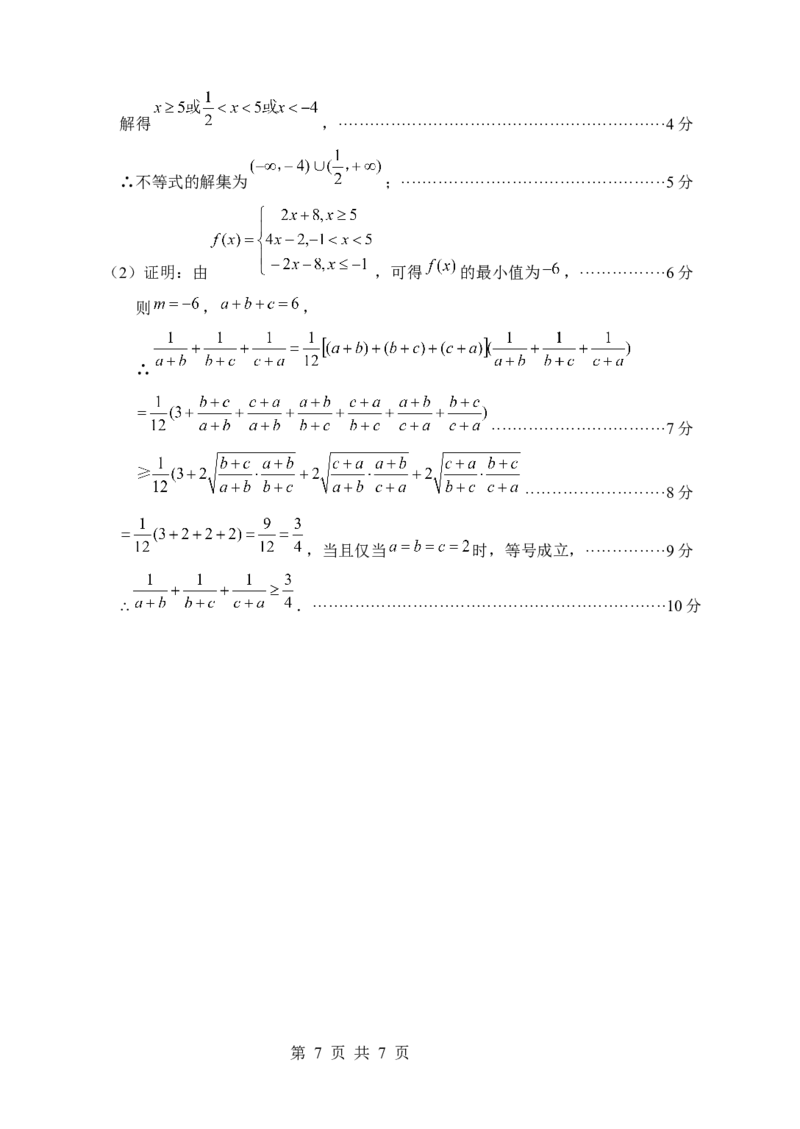文科数学答案_2023年11月_01每日更新_02号_2024届四川省绵阳市高三上学期第一次诊断性考试_2024届四川省绵阳市高三上学期第一次诊断性考试文科数学

绵阳市高中2021级第一次诊断性考试 文科数学参考答案及评分意见 一、选择题：本大题共12小题，每小题5分，共60分． BBCAD BACBC BC 二、填空题：本大题共4小题，每小题5分，共20分． 13．7 14． 15． 16．1 三、解答题：本大题共6小题，共70分． 17．解：（1）由S，2S，3S 成等差数列，则4S=S+3S，得3a=a，················3分 1 2 3 2 1 3 3 2 ∴数列{a}的公比q ，·····································································4分 n 由 ，数列{a}的通项公式 ；··································6分 n （2）令 ，则 ，·········································8分 ∴当 时， ，········································································9分 ∴当 或4时，T 取得最大值： ．····························12分 n 8．解：（1）∵ ， 1 ，而 ，····························································2分 ∴ ∴ ， 即 ，·························································3分 的最小正周期为： ；··················································4分 ∴ 由题意， ，····················································5分 （2） 第 1 页 共 7 页， ∵ ，··································7分 ∴ Z，·······························································9分 ∴ ，·····················································10分 ∴ ∴ 的最小值为 ．··········································································12分 19．解：（1）∵ 为奇函数， ∴ ，解得：m=2．···························································5分 （2）当m>0时，2x2+m>0 ， ∴函数 不可能有两个零点．································6分 当m <0时，由 ，解得： 或m2，································7分 要使得f(x)仅有两个零点，则 ，··········································8分 即 ，此方程无解． 故m=0，即 ，·······························································9分 令 ，则 ， ，解得： 或 ， 解得： ， 故 在 ， 上递增，在 上递减，···························10分 第 2 页 共 7 页又 ， 故函数 仅有一个零点．·························································12分 20．解：（1）∵cos(CB)sinA=cos(CA)sinB (cosCcosB+sinCsinB)sinA=(cosCcosA+sinCsinA)sinB··································2分 ∴ ∴cosCcosBsinA=cosCcosAsinB································································3分 又∵△ABC为斜三角形，则cosC≠0， ∴cosBsinA=cosAsinB，·········································································5分 ∴sin(AB)=0，又A，B为△ABC的内角， ∴A=B；····························································································6分 （2）在△ABC中，由（1）知，a=b， ，则 ，···············································7分 由正弦定理 又 ，即 ， ， ∴ ∴ ==sin2Bsin22B，··································································9分 ∴ =sin2Bsin22B=sin2B4cos2Bsin2B=sin2B4(1sin2B)sin2B，··············10分 令sin2B=t，令f(t)=t4(1t)t=4t23t，·······················································11分 2B<1，即0＜t<1， 又因为0＜sin ∴当t= 时，f(t)取最小值，且f(t) = ， min 综上所述： 的最小值为 ．···················································12分 第 3 页 共 7 页21．解：（1）方法一： ，························································1分 因为 在 上单调递增， ∴ 恒成立， 故：当 时， 恒成立．·····················································3分 设 ，则 ， 则 ， 易知 ，所以 ， 故令 得到： ；令 得到： ． ∴ 在 上递减；在 上递增．·············································5分 故：当 时， ． ∴实数a的取值范围： ．···························································6分 方法二： ， 因为 在 上单调递增，所以 恒成立， 等价于： 在 上恒成立，········································2分 设 ，则 ， ， 当 时， ， ∴ 在 上递减， ，符合题意．····························3分 当 时，易知 在 上递减，在 上递增，在 上递减， 因为 ， 故只需满足 （由 易得），符合题意．·················4分 当 时，易知 在(1，a)上递减，在(a，2)上递增，在 上递减， 第 4 页 共 7 页因为 ，故只需满足 ，即 ， 当 时，易知 在(1，2)上递增，在 上递减，························5分 ，不符合题意． 综上：实数a的取值范围： ．·····················································6分 （2） 的极值点个数等价于 的变号零点个数， 令 ，则等价于 的变号零点个数，···························7分 当 时， ；当 时， ， 由（1）可知 ， ， 当 时，易知 在 上递减，故 有唯一变号零点1；·······8分 当 时，易知 在 上递减，在 上递增，在 上递减， 因为 ， ，故 有唯一变号零点1； 当 且 时，易知 在 上递减，在(a，2)上递增，在 上递 减，·······································································································9分 ， ， 若 ，即 时，有唯一变号零点1；···································10分 若 ，即 且 时， 有三个变号零点1， ， ， 且 。 当 时，易知 在 上递减， 在(1，2)上递增，在 上递减，·····················································11分 由于 ， ， 有唯一变号零点 ，且 . 综上：当 且 时， 有三个极值点； 当 或 时， 有唯一极值点．·············································12分 第 5 页 共 7 页22．解：（1）曲线C 的参数方程为C ： （t为参数）， 1 1 由 得C 的普通方程为： ；······································2分 1 曲线C 的参数方程为C ： （ 为参数）， 2 2 所以C 的普通方程为： ；············································4分 2 （2）曲线C 的极坐标方程为： ，···············5分 1 ∴ ，·················································································6分 由 得： ， ∴射线： 与曲线C 交于A ，·····································7分 1 曲线C 的极坐标方程为 ， 2 由 得： ， ∴射线： 与曲线C 交于B ，····································9分 2 则 = = ．······················10分 23．解：（1） ···································1分 ∴ ，································2分 第 6 页 共 7 页解得 ，······························································4分 ∴不等式的解集为 ；··················································5分 （2）证明：由 ，可得 的最小值为 ，················6分 则 ， ， ∴ ·································7分 ··························8分 ，当且仅当 时，等号成立，···············9分 ∴ ．···································································10分 第 7 页 共 7 页