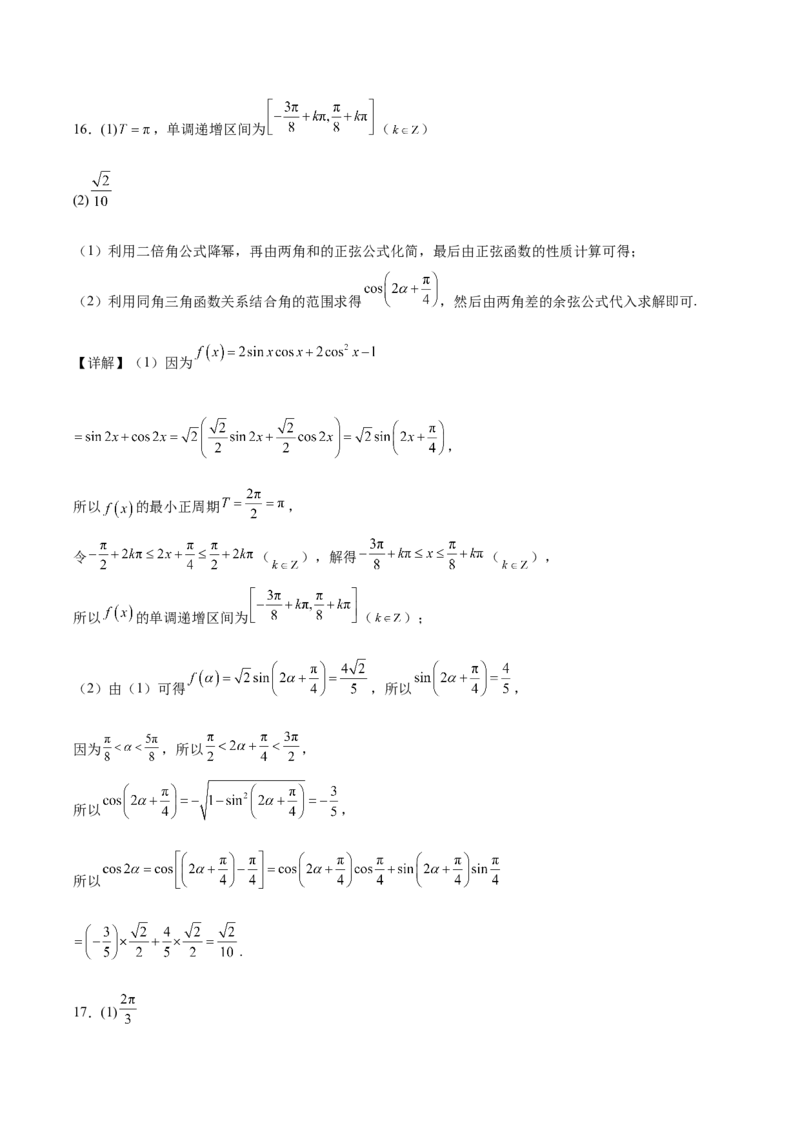文档内容
山西省晋城市部分学校2024-2025学年高一下学期期中考试
数学试题
一、单选题
1.已知集合 ,则 ( )
A. B.
C. D.
2.已知复数 ,则 的虚部为( )
A. B.2 C. D.
3.已知 , ,则与 同方向的单位向量为( )
A. B. C. D.
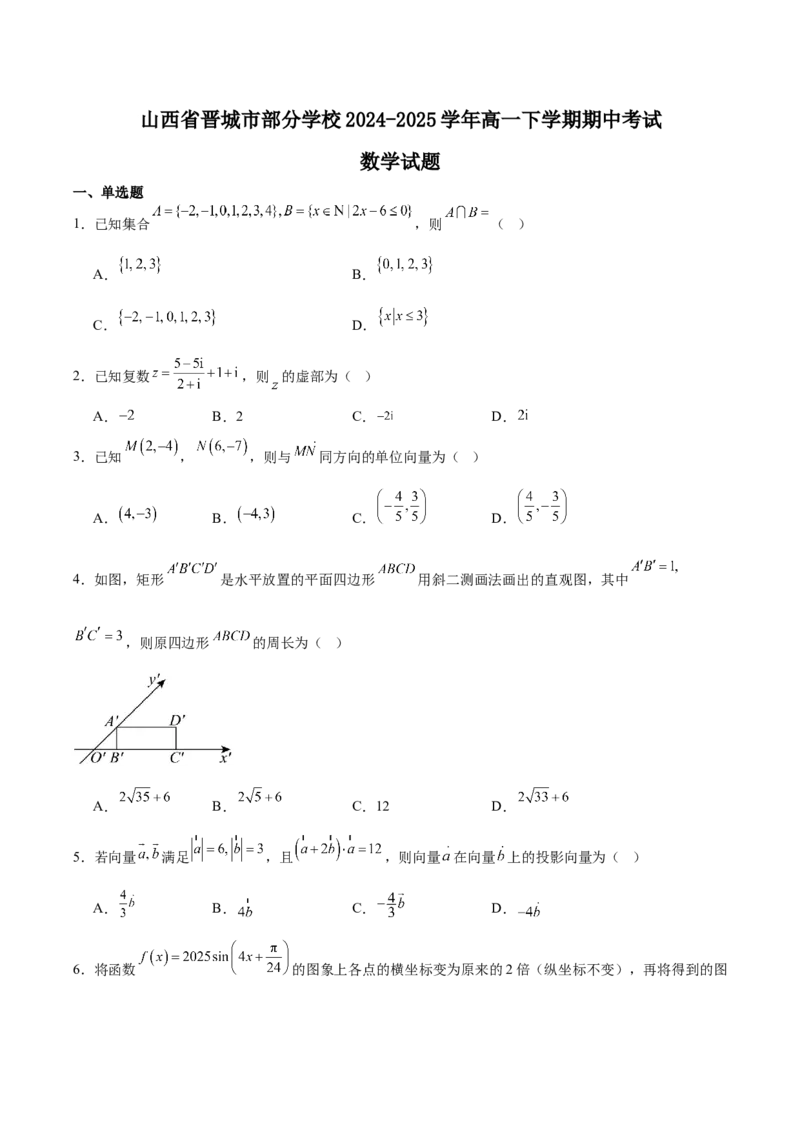
4.如图,矩形 是水平放置的平面四边形 用斜二测画法画出的直观图,其中
,则原四边形 的周长为( )
A. B. C.12 D.
5.若向量 满足 ,且 ,则向量 在向量 上的投影向量为( )
A. B. C. D.
6.将函数 的图象上各点的横坐标变为原来的2倍(纵坐标不变),再将得到的图象向右平移 个单位长度,所得图象的解析式为( )
A. B.
C. D.
7.在平行四边形 中, ,点 满足 ,点 是 的中点,则
( )
A. B. C. D.
8.已知函数 的定义域为 , 为偶函数,若对任意的 ,都有
,则关于 的不等式 的解集为( )
A. B. C. D.
二、多选题
9.下列说法正确的是( )
A.有一个面是多边形,其余各面都是三角形的几何体叫做棱锥
B.棱柱至少有五个面
C.棱台的侧棱延长后必交于一点
D.以直角梯形的一腰为轴旋转所形成的旋转体是圆台
10.已知复数 满足 ,则下列说法正确的是( )
A. B.
C. D. 是关于 的方程 的一个根11.如图,在边长为2的正方形 中,点 是 的中点,点 满足
,则下列说法正确的是( )
A.若 ,则
B.若 ,则 为定值
C.若点 在线段 上,则 为定值
D.若 ,则 的最大值为
三、填空题
12.某圆锥的侧面展开图是半径为4,圆心角为 的扇形,则该圆锥的底面直径为 .
13.已知 ,复数 在复平面内对应的点位于第四象限,则实数 的取值范围是 .
14.已知 的内角 的对边分别为 ,且 ,则 ;若
的外接圆的圆心是 ,则 的最大值为 .
四、解答题
15.已知向量 .
(1)设 ,求 的值;
(2)若 ,求 的值.16.已知函数 .
(1)求 的最小正周期和单调递增区间;
(2)若 且 ,求 的值.
17.在 中,内角 的对边分别为 ,且 .
(1)求角 的大小;
(2)若点 是线段 上的一点,且 ,求 的值.
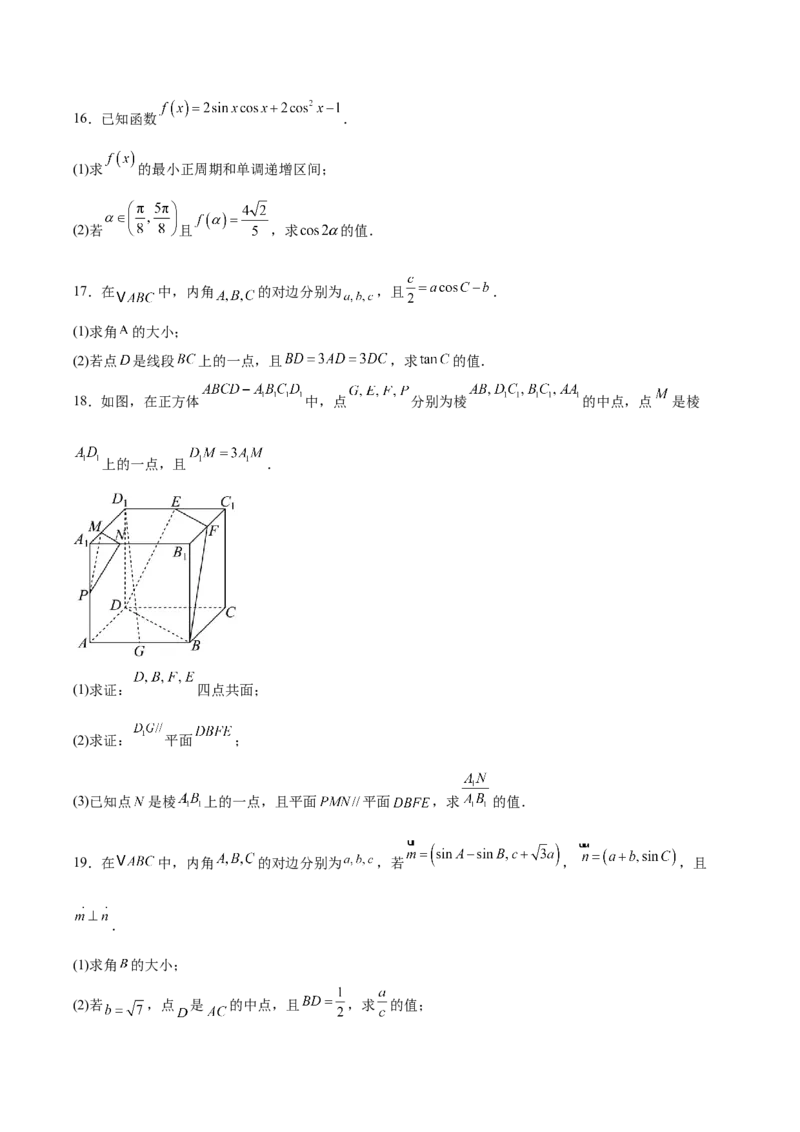
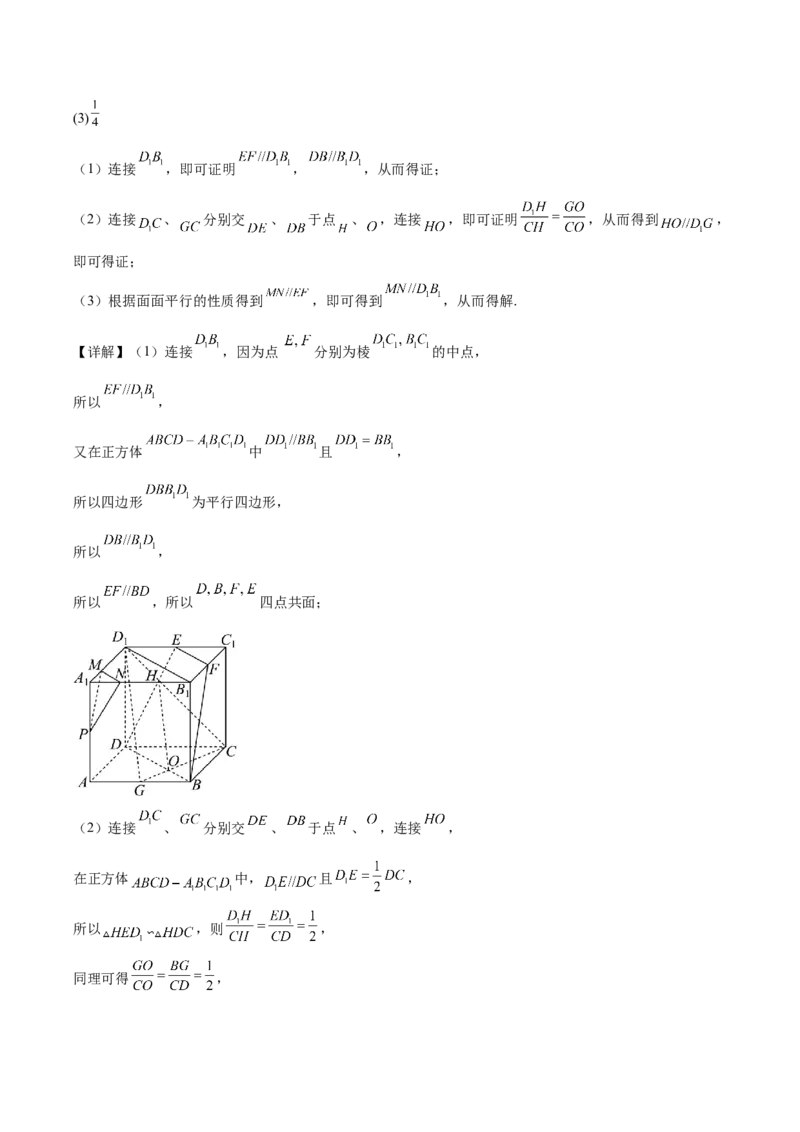
18.如图,在正方体 中,点 分别为棱 的中点,点 是棱
上的一点,且 .
(1)求证: 四点共面;
(2)求证: 平面 ;
(3)已知点 是棱 上的一点,且平面 平面 ,求 的值.
19.在 中,内角 的对边分别为 ,若 , ,且
.
(1)求角 的大小;
(2)若 ,点 是 的中点,且 ,求 的值;(3)已知 的面积为 ,且 所在平面内的点 满足 ,求
的值.题号 1 2 3 4 5 6 7 8 9 10
答案 B A D C C D B C BC ABD
题号 11
答案 BCD
1.B
根据题意,求得 ,结合集合交集的概念与运算,即可求解.
【详解】由集合 ,
又由集合 ,所以 .
故选:B.
2.A
先利用复数的除法运算和加法运算化简,再根据虚部的定义即可得出.
【详解】 ,
则 的虚部为 .
故选:A
3.D
求出向量 的坐标,即可得出与 同方向的单位向量为 .
【详解】由题意可得 ,则 ,
所以与 同方向的单位向量为 .
故选:D.
4.C
由题意,结合斜二测画法将直观图还原为原图,进而求解.
【详解】由题意知, ,
将直观图还原为原图,如图,则 ,
所以 ,
所以原四边形 的周长为12.
故选:C
5.C
根据数量积的运算律求出 ,再由投影向量的定义计算可得.
【详解】因为 ,且 ,
所以 ,解得 ,
所以向量 在向量 上的投影向量 .
故选:C
6.D
根据三角函数的变换规则计算可得.
【详解】将函数 的图象上各点的横坐标变为原来的2倍(纵坐标不变)得到
,
将 的图象向右平移 个单位长度得到 .
故选:D
7.B用 、 作为基底表示出 、 ,再由数量积的运算律及定义计算可得.
【详解】因为 且点 是 的中点,
所以 ,
又 ,
所以
.
故选:B
8.C
首先可得 关于 对称且 在 上单调递增,则关于 的不等式 等价
于 ,再分 、 两种情况讨论,结合指数函数的性质解得即可;
【详解】因为 为偶函数,所以 关于 对称,
又对任意的 ,都有 ,
所以 在 上单调递增,则在 上单调递减,
则关于 的不等式 等价于 ,即 ,当 时,不等式可化为 ,即 ,
因为 ,所以不等式无解;
当 时,不等式可化为 ,即 ,即 ,
所以 ,解得 ;
综上可得关于 的不等式 的解集为 ;
故选:C
9.BC
根据空间几何体的结构特征,结合选项依次判断即可.
【详解】A:若其余各面三角形没有公共顶点(如下图),则几何体不是棱锥,故A错误;
B:面最少的就是三棱柱,共有五个面,故B正确;
C:由棱台的结构特征知,棱台的侧棱延长后必交于一点,故C正确;
D:在直角梯形中 ,如下图所示:
以直角梯形的直角边 所在的直线为轴旋转所得的旋转体是圆台,
若以直角梯形的腰 所在的直线为轴旋转所得的旋转体不是圆台,故D错误.
故选:BC
10.ABD
化简复数 ,利用共轭复数的定义以及复数的模的定义可判断AB;利用复数的乘法运算法则计算即可判断C ;因 是 的根,并将 因式分解即可判断D.
【详解】由题意可得, ,
则 , ,故A正确;B正确;
,
则 ,故C错误;
由C选项可知, 是 的根,
又 ,则 是 的一个根,故D正确.
故选:ABD
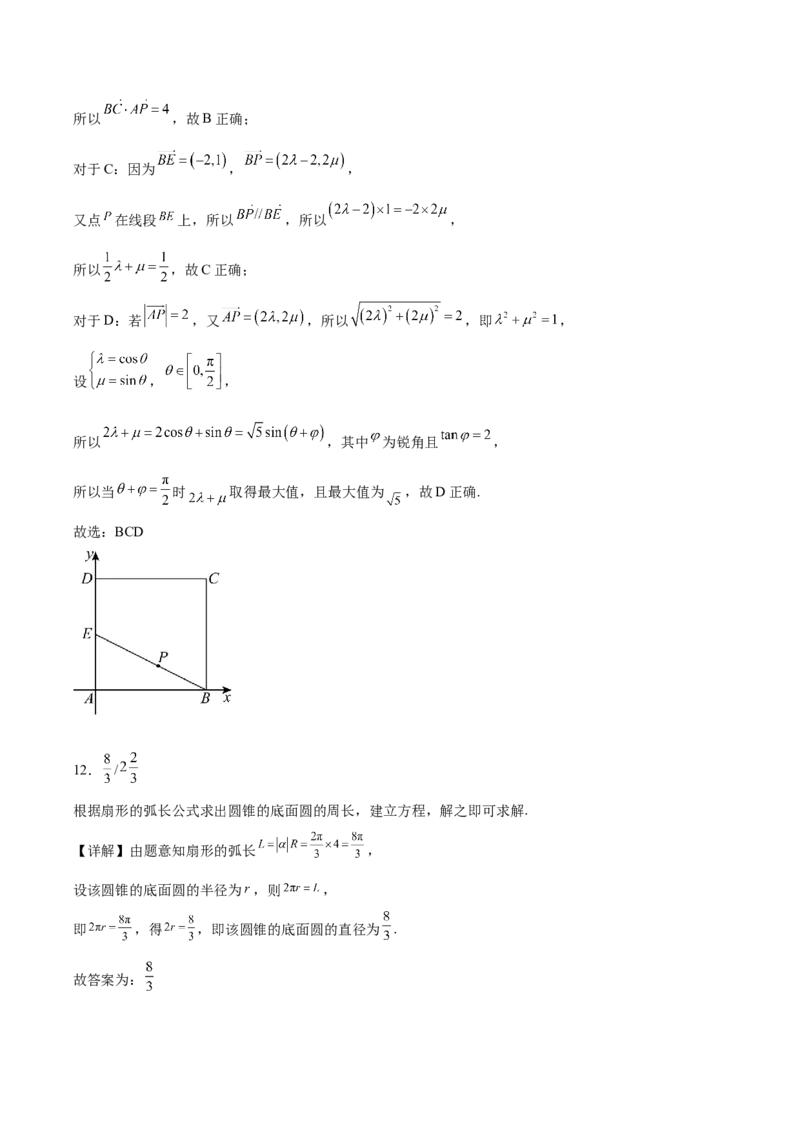
11.BCD
建立如图所示平面直角坐标系,利用坐标法判断A、B,由 及向量共线的坐标表示判断C,根据向
量模的坐标表示得到 ,设 , ,利用辅助角公式计算D.
【详解】如图建立平面直角坐标系,则 , , , , ,
所以 , ,因为
所以 ,即 ;
对于A:若 ,则 ,所以 , ,所以 ,故A错误;
对于B:当 时, ,所以 ,又 ,所以 ,故B正确;
对于C:因为 , ,
又点 在线段 上,所以 ,所以 ,
所以 ,故C正确;
对于D:若 ,又 ,所以 ,即 ,
设 , ,
所以 ,其中 为锐角且 ,
所以当 时 取得最大值,且最大值为 ,故D正确.
故选:BCD
12. /
根据扇形的弧长公式求出圆锥的底面圆的周长,建立方程,解之即可求解.
【详解】由题意知扇形的弧长 ,
设该圆锥的底面圆的半径为 ,则 ,
即 ,得 ,即该圆锥的底面圆的直径为 .
故答案为:13.
根据复数的乘、除法运算可得 ,结合复数的几何意义建立不等式组,解之即可求解.
【详解】 ,
所以 在复平面内对应的点的坐标为 ,位于第四象限,
则 ,解得 ,
即实数 的取值范围为 .
故答案为:
14.
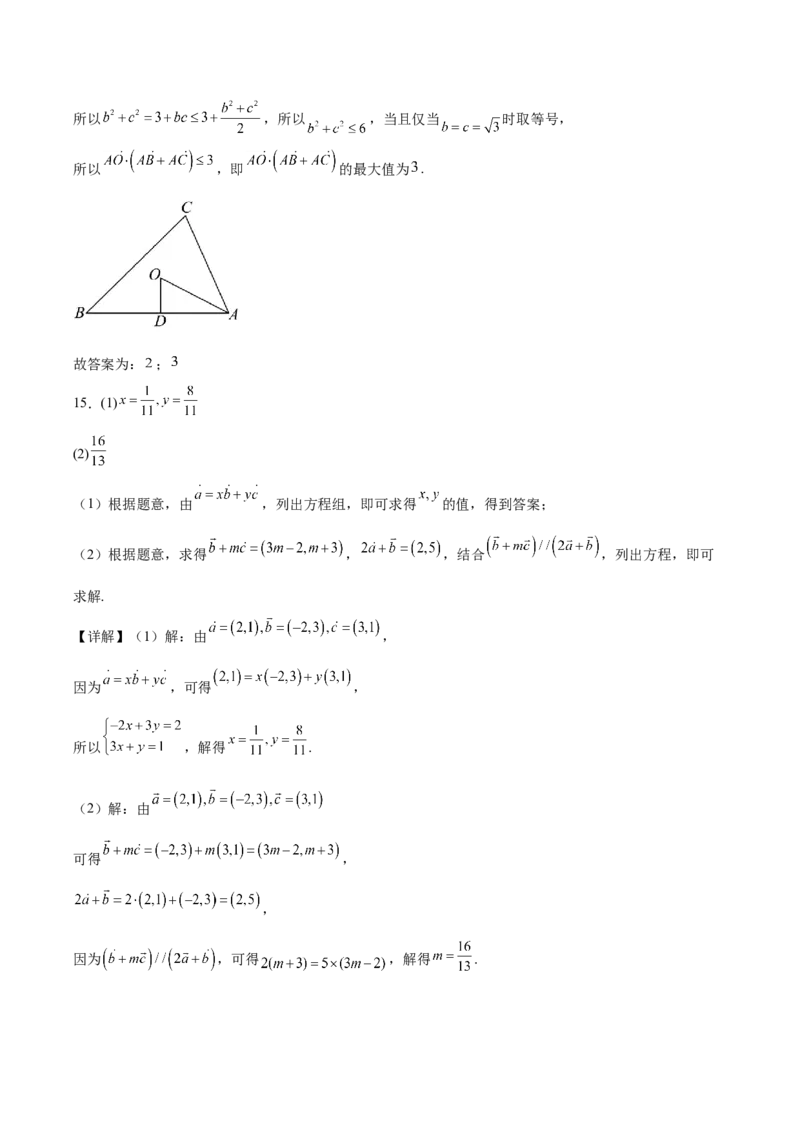
空1:由正弦定理边化角即可求解;空2:取 的中点 ,连接 ,则 ,则 ,从
而得到 ,再由余弦定理及基本不等式求出 的最大值,即可得解.
【详解】由正弦定理得 ,则 , ,
所以 ;
取 的中点 ,连接 ,则 ,
所以 ,
同理可得 ,
所以 ,
由余弦定理 ,即 ,所以 ,所以 ,当且仅当 时取等号,
所以 ,即 的最大值为 .
故答案为: ;
15.(1)
(2)
(1)根据题意,由 ,列出方程组,即可求得 的值,得到答案;
(2)根据题意,求得 , ,结合 ,列出方程,即可
求解.
【详解】(1)解:由 ,
因为 ,可得 ,
所以 ,解得 .
(2)解:由
可得 ,
,
因为 ,可得 ,解得 .16.(1) ,单调递增区间为 ( )
(2)
(1)利用二倍角公式降幂,再由两角和的正弦公式化简,最后由正弦函数的性质计算可得;
(2)利用同角三角函数关系结合角的范围求得 ,然后由两角差的余弦公式代入求解即可.
【详解】(1)因为
,
所以 的最小正周期 ,
令 ( ),解得 ( ),
所以 的单调递增区间为 ( );
(2)由(1)可得 ,所以 ,
因为 ,所以 ,
所以 ,
所以
.
17.(1)(2)
(1)利用正弦定理将边化角,再由两角和的正弦公式计算可得;
(2)设 ,则 , ,在 中利用正弦定理得到关于 的方程,利用和
差角公式化简可得.
【详解】(1)因为 ,
由正弦定理可得 ,
所以 ,
即 ,
又 ,所以 ,所以 ,又 ,所以 ;
(2)设 ,又 ,所以 ,
则 , ,
在 中,由正弦定理 ,又 ,
所以 ,即 ,
所以 ,即 ,
所以 ,即 .
18.(1)证明见解析
(2)证明见解析(3)
(1)连接 ,即可证明 , ,从而得证;
(2)连接 、 分别交 、 于点 、 ,连接 ,即可证明 ,从而得到 ,
即可得证;
(3)根据面面平行的性质得到 ,即可得到 ,从而得解.
【详解】(1)连接 ,因为点 分别为棱 的中点,
所以 ,
又在正方体 中 且 ,
所以四边形 为平行四边形,
所以 ,
所以 ,所以 四点共面;
(2)连接 、 分别交 、 于点 、 ,连接 ,
在正方体 中, 且 ,
所以 ,则 ,
同理可得 ,所以 ,所以 ,
又 平面 , 平面 ,所以 平面 ;
(3)因为平面 平面 ,
平面 平面 ,平面 平面 ,
所以 ,
又 ,所以 ,因为 ,所以 .
19.(1)
(2) 或
(3) 或
(1)依题意可得 ,根据数量积的坐标表示及利用正弦定理将角化边,再结合余弦定理计算可得;
(2)依题意可得 ,将两边平方结合数量积的运算律以及余弦定理得到方程组,即可求出
、 ,从而得解;
(3)由面积公式求出 ,再分点 与点 在直线 的异侧与同侧两种情况讨论,设 ,利用正
弦定理表示出线段的长度,再计算可得.
【详解】(1)因为 , ,且 ,
所以 ,
由正弦定理可得 ,
即 ,
由余弦定理 ,又 ,所以 ;(2)因为点 是 的中点,所以 ,
所以 ,
所以 ,即 ,
由余弦定理 ,即 ,
解得 或 ,所以 或 ;
(3)因为 的面积为 ,所以 ,所以 ,
若点 与点 在直线 的异侧,设 ,
则 , , ,
在 中由正弦定理 ,所以 , ;
在 中由正弦定理 ,所以 ,
;
所以;
若点 与点 在直线 的同侧,设 ,
则 , , ,
在 中由正弦定理 ,所以 , ;
在 中由正弦定理 ,所以 ,
;
所以
;
综上可得 的值为 或 .