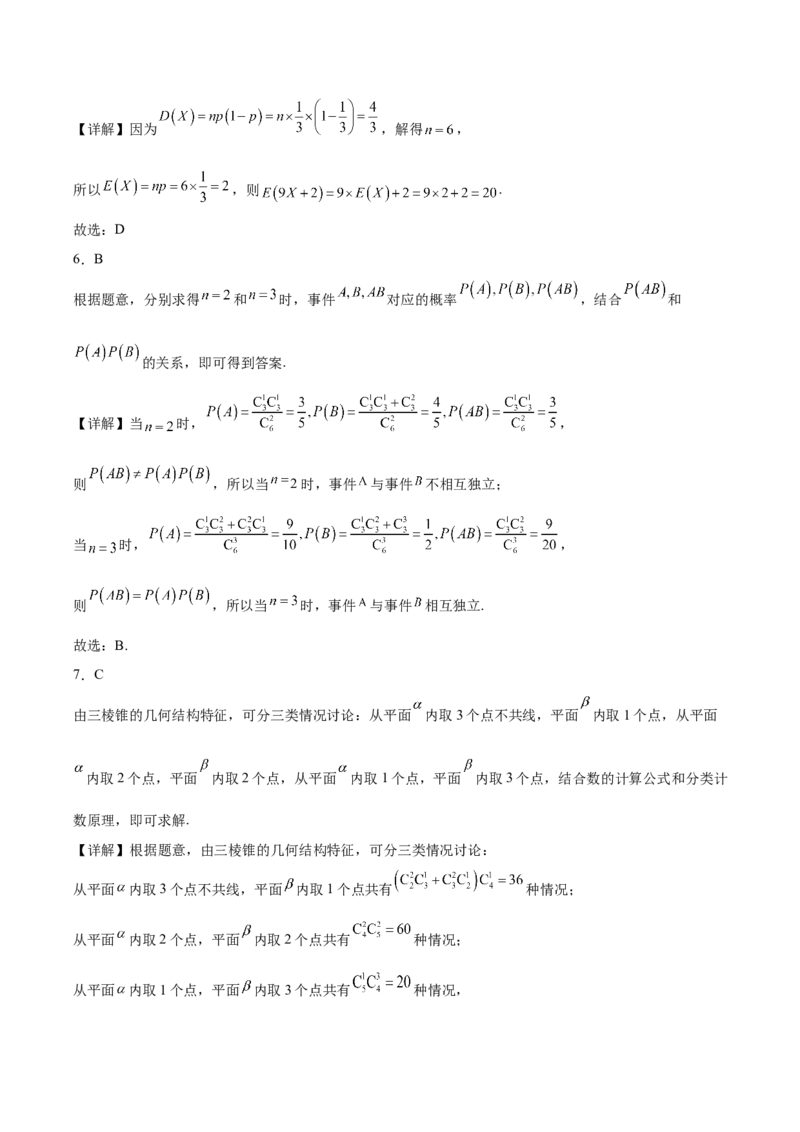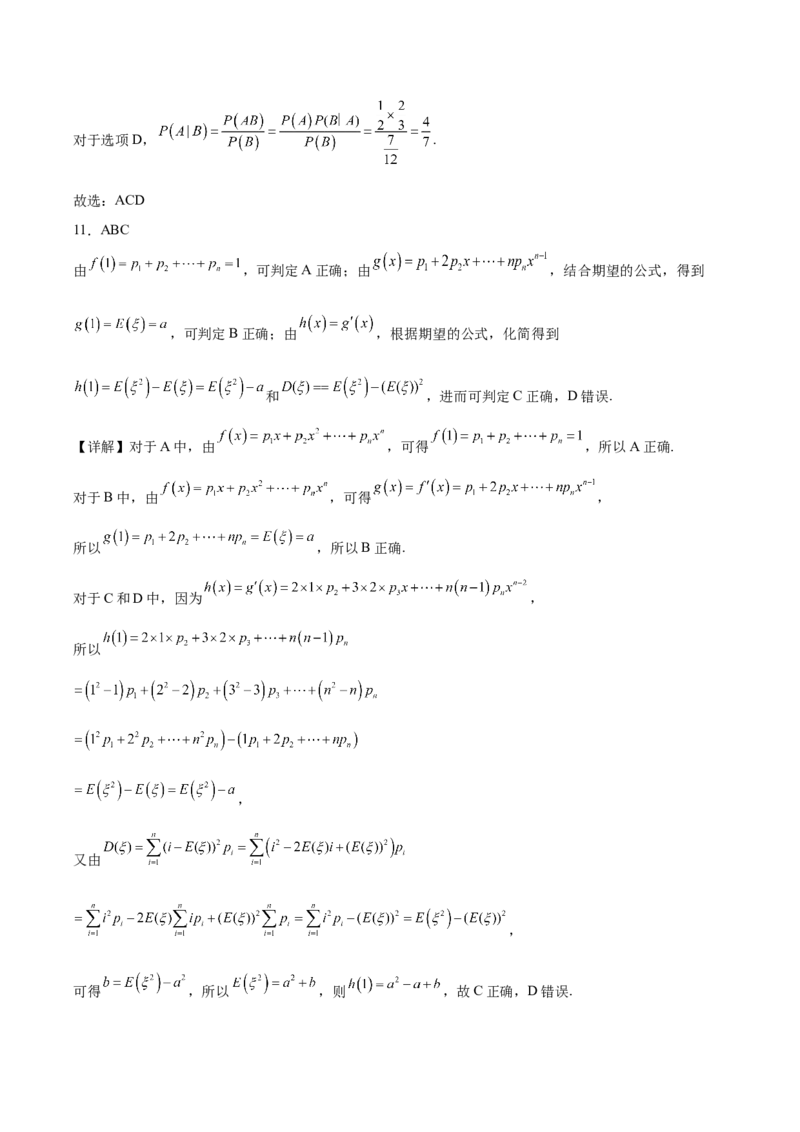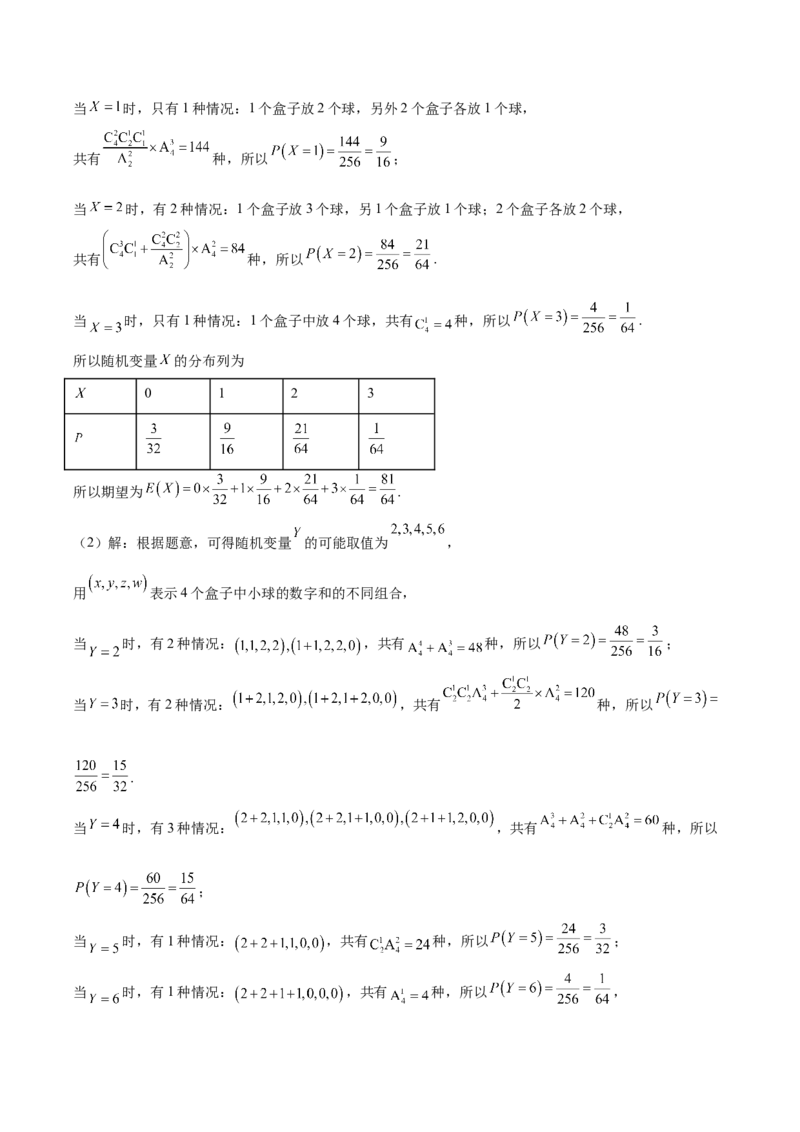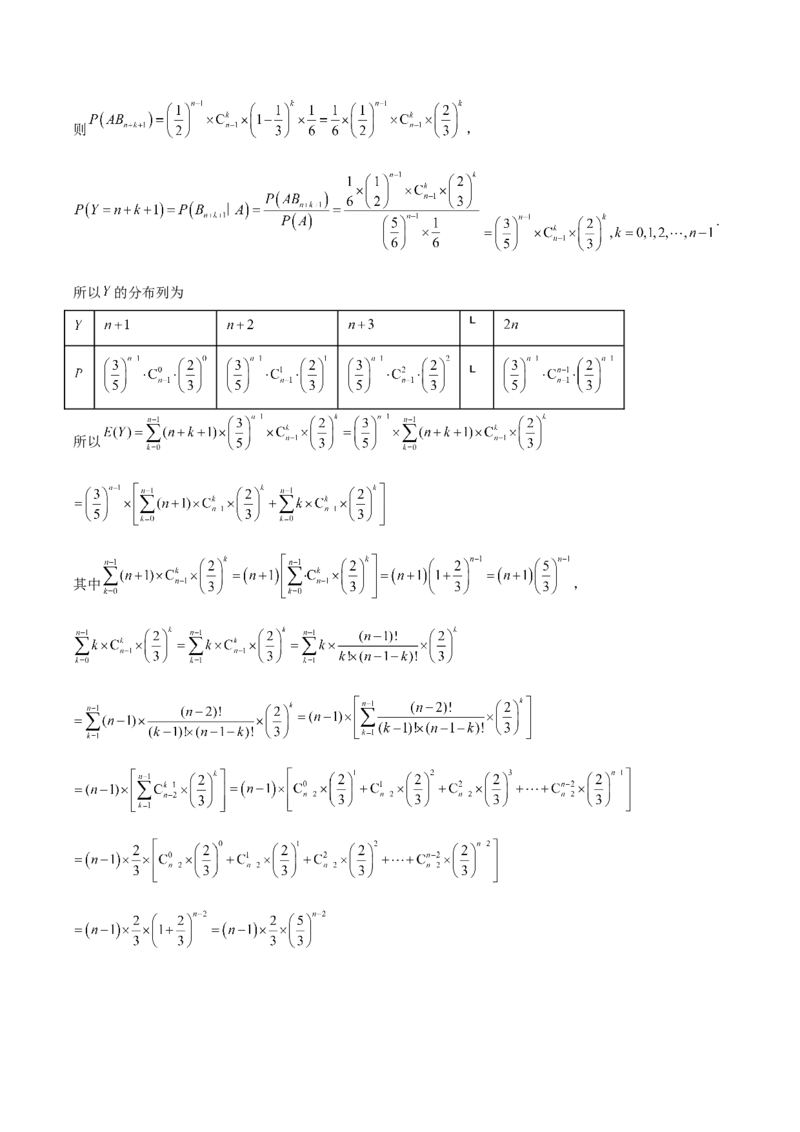文档内容
山西省部分学校2024-2025学年高二下学期期中测评考试
数学试题
一、单选题
1.若 ,则 ( )
A.4 B.7 C.3或7 D.4或7
2.为维护市场秩序,保护消费者权益,在“五一”假期来临之际,物价部门对某商品在各商场的售价
(元)及其一天的销售量 (件)进行调查,得到了若干对数据 ,经过分析,计算,得到 关于
的经验回归方程为 ,则样本点 的残差为( )
A. B. C.1 D.2
3.已知随机变量 服从正态分布 ,且 ,则 ( )
A.1 B.2 C.3 D.4
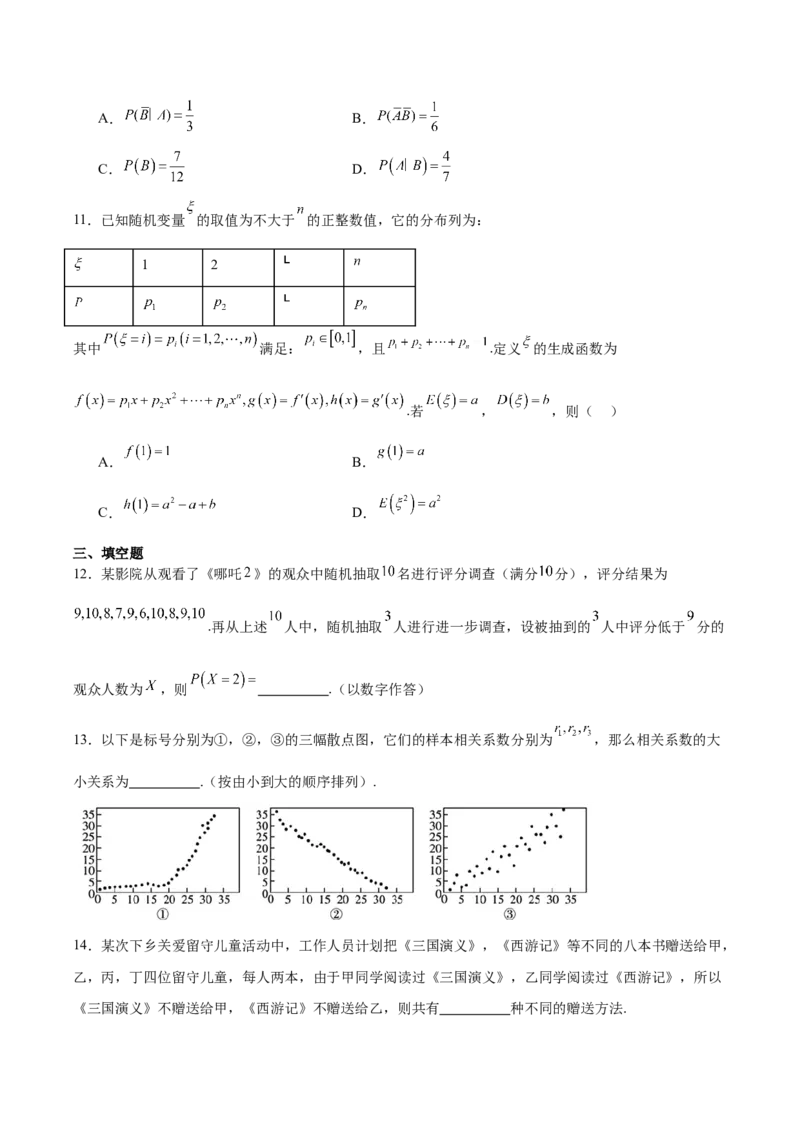
4.下图为根据某组成对数据绘制的散点图,根据最小二乘法得到了经验回归直线1(实线)与经验回归曲
线2(虚线)如图,并分别计算了两模型的决定系数 ,则( )
A. B.
C. D.
5.已知随机变量 服从二项分布 ,且 ,则 ( )
A.10 B.16 C.18 D.20
6.一口袋中有3个红球和3个白球,从中不放回地取出 个,设事件 :取出的 个球既有红球又有白球,
事件 :取出的 个球最多有一个红球,则( )A.当 时事件 与事件 相互独立,当 时事件 与事件 相互独立
B.当 时事件 与事件 不相互独立,当 时事件 与事件 相互独立
C.当 时事件 与事件 相互独立,当 时事件 与事件 不相互独立
D.当 时事件 与事件 不相互独立,当 时事件 与事件 不相互独立
7.已知平面 平面 ,平面 内有 共5个点,其中有且仅有 三点共线,平面 内有
共4个点,任意三点不共线,则以这9个点为顶点的三棱锥最多有( )
A.80个 B.86个 C.116个 D.136个
8. 展开式中二项式系数构成杨辉三角,人们在研究
展开式时,发现各项系数也可以构成一个类似的三角形,并把
它称为“广义杨辉三角”,如图所示,则 ( )
A. B. C. D.
9.可用于推断两个分类变量之间是否有关联的是( )
A.散点图 B.等高堆积条形图
C.列联表 D. 独立性检验
二、多选题
10.为了增强学生国防意识,某校组织学生进行了一次打靶射击活动.小王同学先后射击两次,第一次命中
靶心的概率为 ,若第一次命中靶心,则第二次命中靶心的概率为 ,若第一次没有命中靶心,则第二次
命中靶心的概率为 ,记第一枪命中靶心为事件 ,第二枪命中靰心为事件 ,则( )A. B.
C. D.
11.已知随机变量 的取值为不大于 的正整数值,它的分布列为:
1 2
其中 满足: ,且 .定义 的生成函数为
.若 , ,则( )
A. B.
C. D.
三、填空题
12.某影院从观看了《哪吒 》的观众中随机抽取 名进行评分调查(满分 分),评分结果为
.再从上述 人中,随机抽取 人进行进一步调查,设被抽到的 人中评分低于 分的
观众人数为 ,则 .(以数字作答)
13.以下是标号分别为①,②,③的三幅散点图,它们的样本相关系数分别为 ,那么相关系数的大
小关系为 .(按由小到大的顺序排列).
14.某次下乡关爱留守儿童活动中,工作人员计划把《三国演义》,《西游记》等不同的八本书赠送给甲,
乙,丙,丁四位留守儿童,每人两本,由于甲同学阅读过《三国演义》,乙同学阅读过《西游记》,所以
《三国演义》不赠送给甲,《西游记》不赠送给乙,则共有 种不同的赠送方法.四、解答题
15.某次考试中,数学成绩可划分为“优秀”、“良好”、“一般”三个等级,一班与二班各等级学生人
数如下表:
优秀 良好 一般
一班 9 13 23
二班 15 14 16
(1)一班、二班数学成绩的优秀率分别是多少?
(2)填写如下列联表,依据小概率值 的 独立性检验,能否推断两班学生的数学成绩优秀率有差异?
优秀 其他 合计
一班
二班
合计
附:
0.100 0.050 0.010
2.706 3.841 6.635
16.已知 ,若 的展开式中二项式系数和为 .
(1)求 ;
(2)求 被15除的余数.
17.标记数字1,2的小球各2个,将这4个不同的小球依次随机地放入4个不同的盒子中.
(1)记空盒子的个数为 ,求 的分布列及数学期望 ;
(2)记4个盒子中小球的数字和分别为 (空盒子中,小球的数字和为0),记 中的最大值为 ,求 的分布列及数学期望 .
18.下表为我国2015年至2023年城镇人口 (单位:亿)的数据,其中年份代码 分别对应年份
,并计算得 与 的样本相关系数
年份代码 1 2 3 4 5 6 7 8 9
城镇人口 亿 7.67 7.93 8.19 8.43 8.64 8.84 9.02 9.14 9.21
(1)求 关于 的回归方程 (系数精确到0.01);
(2)预测2025年我国乡村人口为4.53亿人,城镇居民平均消费水平为4.26万元,农村居民平均消费水平为
2.24万元,试预测2025年我国居民平均消费水平(精确到0.01);
(3)若变量 和 的 对观测数据为 ,
则称 为样本协方差,其中 .
基于我国2015年至2023年城镇人口 (单位:亿)的数据,求协方差 (精确到0.01);
①
一般地,如何通过协方差 的取值判断随机变量 和 是否正负相关?协方差 的大
②
小一定能度量出 和 的线性相关程度吗?样本相关系数相比协方差 有何优点?
附:样本相关系数 .
回归方程 中斜率和截距的最小二乘估计公式分别为:
19.近年来国产芯片技术日趋成熟,其中有一项工艺称为“二次曝光技术”,即在同一块晶片上先进行一
次曝光,清洗,然后再进行一次曝光.只有两次曝光都成功,该晶片方可成功制作成1块芯片.假设第一次曝光的成功率为 ,第二次曝光的成功率为 ,每次曝光过程相互独立.现要制作1块芯片,依次对 块晶片
进行曝光,操作要求如下:
若对第 块晶片进行第一次曝光失败,则不继续对该晶片进行第二次曝光,并认为对该
①
晶片的制作失败,接着对第 块晶片进行曝光;
若对第 块晶片进行第一次曝光成功,则继续对该晶片进行第二次曝光,若第二次曝光
②
失败,则也认为对该晶片的制作失败,接着对第 块晶片进行曝光;若第二次曝光成功,即成功制作出
1块芯片,则不再对后续的晶片进行曝光;
若对这 块晶片都曝光完毕,无论是否成功制作出1块芯片,则停止制作.
③(1)当 时,求成功制作出至少1块芯片的概率;
(2)用这 块晶片制作1块芯片,记随机变量 为曝光的晶片个数,求 的分布列和数学期望 ;
(3)若一块晶片第一次曝光失败,则记该芯片曝光1次;若一块晶片第一次曝光成功,无论第二次曝光成功
还是失败,都记该芯片共曝光2次.在曝光完这 块晶片,并成功制作出1块芯片的条件下,记随机变量
为这 块晶片曝光的总次数,求 的数学期望 .题号 1 2 3 4 5 6 7 8 9 10
答案 C A A C D B C B BCD ACD
题号 11
答案 ABC
1.C
根据组合数公式的性质计算可得.
【详解】因为 ,所以 或 ,解得 或 .
故选:C
2.A
根据题意,令 时,求得 ,结合残差的概念,即可求得样本点的残差,得到答案.
【详解】由 关于 的回归方程为 ,且样本点 ,
当 时,可得 ,所以残差为 .
故选:A.
3.A
根据正态分布的对称性即可求解.
【详解】因为 ,
由正态分布关于均值对称可得 ,解得 .
故选: .
4.C
根据决定系数 越大,拟合效果越好,结合图象即可判断
【详解】由图可知,模型2拟合效果更好,故 .
故选: .
5.D
应用二项分布的方差 ,计算求得 ,结合二项分布的期望计算可得结果.【详解】因为 ,解得 ,
所以 ,则 .
故选:D
6.B
根据题意,分别求得 和 时,事件 对应的概率 ,结合 和
的关系,即可得到答案.
【详解】当 时, ,
则 ,所以当 2时,事件 与事件 不相互独立;
当 时, ,
则 ,所以当 时,事件 与事件 相互独立.
故选:B.
7.C
由三棱锥的几何结构特征,可分三类情况讨论:从平面 内取3个点不共线,平面 内取1个点,从平面
内取2个点,平面 内取2个点,从平面 内取1个点,平面 内取3个点,结合数的计算公式和分类计
数原理,即可求解.
【详解】根据题意,由三棱锥的几何结构特征,可分三类情况讨论:
从平面 内取3个点不共线,平面 内取1个点共有 种情况;
从平面 内取2个点,平面 内取2个点共有 种情况;
从平面 内取1个点,平面 内取3个点共有 种情况,所以从这9个点为顶点的三棱锥最多有 个三棱锥.
故选:C.
8.B
根据已知新定义结合二项式展开式计算求解即可.
【详解】由题意可得 ,
根据二项式定理可得 ,
所以 是 的展开式中 项的系数,
又二项展开式 的通项为 ,
令 得 ,
所以 .
故选:B.
9.BCD
根据散点图,等高堆积条形图,列联表和 独立性检验的概念,即可得到答案.
【详解】散点图适用于推断两个定量变量之间是否有相关关系,
其中等高堆积条形图,列联表, 独立性检验适用于推断两个分类变量之间是否有关联.
故选:BCD.
10.ACD
利用条件概率公式计算各选项中的概率值,逐一验证每个选项的正确性,即可得出结果.
【详解】由已知可得 ,
对于选项A, ;
对于选项B, ;
对于选项C, ;对于选项D, .
故选:ACD
11.ABC
由 ,可判定A正确;由 ,结合期望的公式,得到
,可判定B正确;由 ,根据期望的公式,化简得到
和 ,进而可判定C正确,D错误.
【详解】对于A中,由 ,可得 ,所以A正确.
对于B中,由 ,可得 ,
所以 ,所以B正确.
对于C和D中,因为 ,
所以
,
又由
,
可得 ,所以 ,则 ,故C正确,D错误.故选:ABC.
12. /
这道题考查的是古典概型和组合数的综合应用.
【详解】 人中评分低于 分的有 人,“ ”表示事件“抽到 人低于 分, 人高于等于 分”,所
以 .
故答案为: .
13.
根据给定的散点图,结合相关性强弱及正负相关求得大小关系.
【详解】图①散点线性相关关系较弱, 接近于0;
图②散点数据负相关,且线性相关程度很强, 接近于 ;
图③散点数据正相关,且线性相关程度较强, 接近于1,
所以相关系数的大小关系为 .
故答案为:
14.
根据题意,先求得每人两本的安排方法的种数,再分别求得《三国演义》赠送给甲、《西游记》赠送给乙、
《三国演义》赠送给甲,同时《西游记》赠送给乙的种数,进而得到答案.
【详解】八本书赠送给四位留守儿童,每人两本共有 种安排方法,
其中《三国演义》赠送给甲的情况有 种;
《西游记》赠送给乙情况有 种;
《三国演义》赠送给甲,同时《西游记》赠送给乙的情况有 种,
所以符合题意的安排方法有 种.故答案为: .
15.(1) ;
(2)表格见解析,认为两班学生的数学成绩优秀率没有差异.
(1)由统计表中数据直接计算可得;
(2)根据已知完善表格,根据公式计算 ,然后查表可知.
【详解】(1)一班共有 人,其数学成绩的优秀率是 ;
二班共有 人,其数学成绩的优秀率是 .
(2)
优秀 其他 合计
一班 9 36 45
二班 15 30 45
合计 24 66 90
可得 ,
依据小概率值 的 独立性检验,认为两班学生的数学成绩优秀率没有差异.
16.(1)
(2)
(1)根据题意,得到 ,解得 ,结合二项展开式的性质,即可求解;
(2)令 ,得到 ;令 ,得到 ,根据二项式 的展开式的
通项特征,得到 ,再由 ,结合二项展
开式的性质,即可得到答案.
【详解】(1)解:由 的展开式中二项式系数和为 ,可得 ,解得 ,
所以 的展开式中 项为: ,所以 .(2)解:令 ,可得 ,
令 ,可得 ,
由 的展开式的通项为 ,
可得 为正数, 为负数,
所以 ,
又由
,
即 能被15整除,
所以 被15除的余数为 .
17.(1)分布列见解析,
(2)分布列见解析,
(1)根据题意,得到随机变量 的可能取值为 ,利用排列数和组合数的计算公式,分别求得相应
的概率,得出随机变量 的分布列,利用期望的公式,求得数学期望;
(2)根据题意,得到随机变量 的可能取值为 ,用 表示4个盒子中小球的数字和的不
同组合,求得相应的概率,得出随机变量 的分布列,利用期望的公式,求得其数学期望;
【详解】(1)解:由题意知,4个小球放入4个盒子中,共有为 种不同的放法,
所以随机变量 的可能取值为 .
当 时,只有1种情况:每个盒子各放1个球,共 种,
所以 ;当 时,只有1种情况:1个盒子放2个球,另外2个盒子各放1个球,
共有 种,所以 ;
当 时,有2种情况:1个盒子放3个球,另1个盒子放1个球;2个盒子各放2个球,
共有 种,所以 .
当 时,只有1种情况:1个盒子中放4个球,共有 种,所以 .
所以随机变量 的分布列为
0 1 2 3
所以期望为 .
(2)解:根据题意,可得随机变量 的可能取值为 ,
用 表示4个盒子中小球的数字和的不同组合,
当 时,有2种情况: ,共有 种,所以 ;
当 时,有2种情况: ,共有 种,所以
.
当 时,有3种情况: ,共有 种,所以
;
当 时,有1种情况: ,共有 种,所以 ;
当 时,有1种情况: ,共有 种,所以 ,所以随机变量 的分布列为
2 3 4 5 6
所以期望为 .
18.(1)
(2) 万元.
(3) ; 答案见解析
① ②
(1)根据表格中的数据,结合平均数,相关系数和回归系数的公式,可得求得 和 的值,即可得到 关
于 的回归方程;
(2)由2025年对应的年份代码为 ,结合(1)中的回归直线方程,即可作出预测;
(3) 由(1)知 ,得到 ,进而求得 的值;
①
根据协方差与样本相关系数同号,得到协方差 的大小与 和 的度量单位有关,不宜直接用
②
它度量成对样本数据线性相关程度的大小;进而得到答案.
【详解】(1)解:由表格中的数据,可得 ,且
.
又由 ,可得 ,
则 ,
所以 关于 的回归方程为 .
(2)解:2025年对应的年份代码为 ,预测2025年我国城镇人口为 亿人,
预测2025年我国居民平均消费水平为 万元.
(3)解: 由题 ,由(1): ,
①
则 ,
所以 .
注意到协方差与样本相关系数同号,
②可得如果协方差为正,说明两个随机变量具有正相关关系;
如果协方差为负,说明两个随机变量具有负相关关系.
协方差 的大小与 和 的度量单位有关,
所以不宜直接用它度量成对样本数据线性相关程度的大小;
如本题中城镇人口 的单位为“亿”,如果将其单位由亿改为万,
则 的大小将变为原来的10000倍,
但单位的改变并不会导致年份代码 与城镇人口 之间相关程度的改变,
样本相关系数相比协方差 ,消除了度量单位的影响,其大小一定能度量出 和 的线性相关程
度.
19.(1)
(2)分布列见解析,
(3)
(1)根据题意,得到成功的概率为 ,失败的概率为 ,结合对立事件的概率计算公式,即可求得成功制
作出1块芯片的概率;(2)根据题意,得到随机变量 的可能取值为 ,结合当 时,概率为
,当 时,概率为 ,列出随机变量 的分布列,求得
再利用乘公比错位相减法求和,即可得到答案;
(3)法一:记事件 “曝光完这 块晶片,并成功制作出1块芯片”,记事件 “曝光的总次数为
次”,根据题意,得到 的可能取值为 ,利用条件概率和独立重复试验的概率的计算公式,
求得相应的概率,列出分布列,求得期望的表达式,结合组合数的计算公式,进行化简,即可得到答案;
法二:考虑前 块晶片中任意某块的曝光情况,记晶片的曝光次数为随机变量 ,事件 “这块晶片
曝光失败”,事件 “这块晶片的曝光次数为 次”,根据条件概率的计算公式,求得
,得到 ,进而得到前 块晶片曝光的总次数的数学期望.
【详解】(1)解:由题意得,用1块晶片制作,成功的概率为 ,失败的概率为 ,
当 时,要成功制作出至少1块芯片,概率为 .
(2)解:由题意,随机变量 的可能取值为 ,
当 时,可得其概率为 ,
当 时,可得其概率为 ,
所以 的分布列为
1 2 3可得期望为
令 ,
则 ,
两式相减,可得
,
所以 .
(3)解:法一:记事件 “曝光完这 块晶片,并成功制作出1块芯片”,记事件 “曝光的总次数
为 次”,可得 ,
对于前 块晶片,每块晶片都至少曝光1次,第 块晶片曝光2次,
另外,对于前 块晶片,有几块晶片进行了第二次曝光,则总曝光次数就多几次,
并且第1到 块晶片,无论曝光几次,每次曝光都是失败的,
而第 块晶片的2次曝光都成功.若前 块晶片中,
则有 块晶片进行了第二次曝光,所以 ,
所以 的可能取值为 ,则 ,
.
所以 的分布列为
所以
其中 ,所以
法二:考虑前 块晶片中任意某块的曝光情况,
由题意,这块晶片无论曝光几次,都是失败的,记这块晶片的曝光次数为随机变量 ,
记事件 “这块晶片曝光失败”,事件 “这块晶片的曝光次数为 次”.
由第(1)小问可知 .
所以 ,
故这块晶片曝光次数的数学期望为 ,
所以前 块晶片曝光的总次数的数学期望为 ,