精选 2024.1~2 新高考新结构联考卷 29 套
试卷版
目录
安徽省2024届“耀正优＋”高三名校期末测试数学试题 1
河北省金太阳联考2024届高三上学期摸底考试数学试题 5
江西省上饶市六校2024届高三第一次联合考试（2月）数学试卷 9
江西省九师联盟2024届高三上学期1月质量检测试数学试题 13
河南省金太阳联考2023-2024学年高三上学期2月期末检测数学试题 17
辽宁省辽东十一所重点高中联合教研体2024届高三高考适应性考试模拟数学试题 22
河北省衡中同卷2023-2024学年高三1月考试数学试题 26
福建省名校联盟全国优质校2024届高三大联考数学试卷 30
浙江省名校协作体2024届高三下学期开学适应性考试数学试题 34
2024年2月第二届“鱼塘杯”高考适应性练习数学试题 38
湖北省新高考联考协作体2023-2024学年高三下学期2月收心考试数学试卷 42
安徽省部分学校2023-2024学年高三下学期春季阶段性检测数学试题 46
甘肃省九师联盟2024届高三下学期2月开学考试数学试题 50
广东省衡水金卷2024届高三年级2月份大联考数学试题 54
江西省重点中学协作体2024届高三第一次联考数学试卷 57
江西省上进联盟2023-2024学年高三下学期一轮总复习（开学考）验收考试数学试卷 61
重庆市缙云教育联盟2024届高三下学期2月月度质量检测数学试题 65
湖南省名校教育联盟2024届高三下学期入学摸底考试数学试题 68
广东省、福建省、甘肃省2023-2024学年高三下学期开学考试金太阳联考数学试题 71
山东省齐鲁名校联盟2024届高三下学期开学质量检测数学试题 75
浙江省名校协作体2023-2024学年高三下学期开学联考数学试题 79
湖南省、贵州省2023-2024学年高三下学期2月开学金太阳联考数学试题 82
河北省2024届高三年级大数据应用调研联合测评(V)数学试题 86
安徽省1号卷A10联盟2024届高三开年考数学试题 90
黑龙江省“六校联盟”2023-2024学年高三下学期联合性适应测试数学试题 94
安徽省六校教育研究会2023-2024学年高三下学期下学期第二次素养测试(2月)数学试题 98
浙江省新阵地教育联盟2024届高三下学期第三次联考(开学考试)数学试题 102
河北省百师联盟2024届高三下学期开学摸底联考数学试题 106
江西省名校教研联盟2024届高三下学期2月开学考试数学试卷 109安徽省 2024 届“耀正优＋”高三名校期末测试
数学试题
第I卷(选择题)
一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求
的。
1.已知集合U=1,2,3,4,5 ,A=2,3 ,B=xx=2k,k∈Z ，则B∩∁ A= ( ) U
A. 4 B. 2,4 C. 1,2 D. 1,3,5
1
2.复数i-
i
3
的虚部是 ( ) .
A.-8 B.-8i C.8 D.8i
3.已知向量a=0,-2
，b=1,t
1
，若向量b在向量a上的投影向量为- a，则a⋅b= ( )
2
5 11
A.-2 B.- C.2 D.
2 2
π
4.在△ABC中，“C= ”是“sin2A+sin2B=1”的 ( )
2
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
5.过点0,-2 与圆x2+y2-4x-1=0相切的两条直线的夹角为α，则cosα= ( )
1 15 1 10
A. B. C.- D.
4 4 4 4
6.A，B，C，D，E五人站成一排，如果A，B必须相邻，那么排法种数为 ( )
A.24 B.120 C.48 D.60
1 7.若系列椭圆C :a x2+y2=1(0<a <1，n∈N*)的离心率e =
n n n n 2
n ，则a = ( )
n
1
A.1-
4
n 1
B.1-
2
n 1
C. 1-
2
n 1
D. 1-
4
n
8.已知等差数列a n (公差不为0)和等差数列b n 的前n项和分别为S 、T ，如果关于x的实系数方程 n n
1003x2-S 1003 x+T 1003 =0有实数解，那么以下1003个方程x2-a i x+b i =0i=1,2,⋯1003 中，有实数解
的方程至少有 ( ) 个.
A.499 B.500 C.501 D.502
二、选择题：本题共3小题，每小题6分，共18分。在每小题给出的选项中, 有多项符合题目要求。全部选对
的得6分，部分选对的得3分，有选错的得0分。
9.已知一组数据：12,31,24,33,22,35,45,25,16，若去掉12和45，则剩下的数据与原数据相比，下列结论正
·1·确的是 ( )
A.中位数不变 B.平均数不变 C.方差不变 D.第40百分位数不变
x2 y2
10.双曲线C： - =1a>0,b>0
a2 b2
，左、右顶点分别为A，B，O为坐标原点，如图，已知动直线l与双曲
线C左、右两支分别交于P，Q两点,与其两条渐近线分别交于R，S两点,则下列命题正确的是 ( )
A.存在直线l，使得AP∥OR
B.l在运动的过程中，始终有PR =SQ
C.若直线l的方程为y=kx+2，存在k，使得S 取到最大值
△ORB
2
D.若直线l的方程为y=- x-a
2
，RS=2SB，则双曲线C的离心率为 3
11.如图所示，有一个棱长为4的正四面体P-ABC容器，D是PB的中点，E是CD上的动点，则下列说法正
确的是 ( )
π
A.直线AE与PB所成的角为
2
B.△ABE的周长最小值为4+ 34
6
C.如果在这个容器中放入1个小球(全部进入)，则小球半径的最大值为
3
2 6-2
D.如果在这个容器中放入4个完全相同的小球(全部进入)，则小球半径的最大值为
5
第II卷(非选择题)
三、填空题：本题共3小题，每小题5分，共15分．
12.小于300的所有末尾是1的三位数的和等于 ．
13.已知函数fx =lnx+1
ax
- ，若fx
x+1
≥0恒成立，则a= .
p
14.已知抛物线C:y2=2px(p>0)，点P为抛物线上的动点，点A4- ,0
2
与点P的距离AP 的最小值为2，
·2·则p= .
四、解答题：本题共5小题，共77分。解答应写出文字说明、证明过程或演算步骤。
15（. 13分）在△ABC中，A,B,C的对边分别为a,b,c，已知b= 2,c=4,acosC+b=0.
(1)求a；
3π
(2)已知点D在线段BC上，且∠ADB= ，求AD长.
4
16（. 15分）甲、乙两人进行射击比赛，每次比赛中，甲､乙各射击一次，甲､乙每次至少射中8环.根据统计资料
可知，甲击中8环､9环､10环的概率分别为0.7,0.2,0.1，乙击中8环､9环､10环的概率分别为0.6,0.2,
0.2，且甲､乙两人射击相互独立.
(1)在一场比赛中，求乙击中的环数少于甲击中的环数的概率；
(2)若独立进行三场比赛，其中X场比赛中甲击中的环数多于乙击中的环数，求X的分布列与数学期望.
17（. 15分）如图，圆台O O 的轴截面为等腰梯形A ACC ，AC=2AA =2A C =4，B为底面圆周上异于A，C
1 2 1 1 1 1 1
的点.
(1)在平面BCC 内，过C 作一条直线与平面A AB平行，并说明理由；
1 1 1
(2)设平面A AB∩平面C CB=l，Q∈l，BC 与平面QAC所成角为α，当四棱锥B-A ACC 的体积最大
1 1 1 1 1
时，求sinα的取值范围.
18（. 17分）已知函数fx =lnx-axx-1 .
(1)当a<0时，探究f x 零点的个数；
(2)当a>0时，证明：fx
2+a 3
≤ - .
a2+8a-a 2
19（. 17分）阿波罗尼斯是古希腊著名数学家，他的主要研究成果集中在他的代表作《圆锥曲线》一书中．阿
MQ
波罗尼斯圆是他的研究成果之一，指的是已知动点 M 与两定点 Q，P 的距离之比
MP
=
λ λ>0,λ≠1 ，λ是一个常数，那么动点M的轨迹就是阿波罗尼斯圆，圆心在直线PQ上．已知动点M
x2 y2
的轨迹是阿波罗尼斯圆，其方程为x2+y2=4，定点分别为椭圆C: + =1 a>b>0
a2 b2
的右焦点F与
1
右顶点A，且椭圆C的离心率为e= ．
2
·3·(1)求椭圆C的标准方程；
(2)如图，过右焦点F斜率为k k>0 的直线l与椭圆C相交于B，D(点B在x轴上方)，点S，T是椭圆C
上异于B，D的两点，SF平分∠BSD，TF平分∠BTD．
BS
①求
DS
的取值范围；
81π
②将点S、F、T看作一个阿波罗尼斯圆上的三点，若△SFT外接圆的面积为 ，求直线l的方程．
8
·4·河北省金太阳联考 2024 届高三上学期摸底考试
数学试题
第I卷(选择题)
一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求
的。
1.已知全集U=A∪B=x∈N0≤x≤8 ，A∩∁ U B =1,3,5 ，则集合B为 ( )
A. 2,4,6,7 B. 0,2,4,6,8 C. 0,2,4,6,7,8 D. 0,1,2,3,4,5,6,7,8
2.已知直线l、m、n与平面α、β，下列命题正确的是 ( )
A.若α⎳β，l⊂α，n⊂β，则l⎳n B.若α⊥β，l⊂α，则l⊥β
C.若l⊥n，m⊥n，则l⎳m D.若l⊥α，l⎳β，则α⊥β
3.若抛物线x2=2py(p>0)上一点Mn,6 到焦点的距离是4p，则p的值为 ( )
12 7 6 7
A. B. C. D.
7 12 7 6
4.在党的二十大报告中，习近平总书记提出要发展“高质量教育”，促进城乡教育均衡发展.某地区教育行
政部门积极响应党中央号召，近期将安排甲､乙､丙､丁4名教育专家前往某省教育相对落后的三个地区
指导教育教学工作，则每个地区至少安排1名专家的概率为 ( )
1 4 1 8
A. B. C. D.
9 9 3 27
5.蚊香具有悠久的历史，我国蚊香的发明与古人端午节的习俗有关.如图为某校数学社团用数学软件制作
的“蚊香”. 画法如下：在水平直线上取长度为1的线段AB，作一个等边三角形ABC，然后以点B为圆心，
AB为半径逆时针画圆弧交线段CB的延长线于点D(第一段圆弧)，再以点C为圆心，CD为半径逆时针
画圆弧交线段AC的延长线于点E，再以点A为圆心，AE为半径逆时针画圆弧⋯⋯以此类推，当得到的
“蚊香”恰好有15段圆弧时，“蚊香”的长度为 ( )
A.44π B.64π C.70π D.80π
6.已知圆C:x2+2x+y2-1=0，直线mx+ny-1 =0与圆C交于A，B两点.若△ABC为直角三角形，则
( )
A.mn=0 B.m-n=0 C.m+n=0 D.m2-3n2=0
·5·7.现有甲、乙两组数据，每组数据均由六个数组成，其中甲组数据的平均数为3，方差为5，乙组数据的平均
数为5，方差为3．若将这两组数据混合成一组，则新的一组数据的方差为 ( )
A.3.5 B.4 C.4.5 D.5
8.“曼哈顿距离”是十九世纪的赫尔曼•闵可夫斯基所创词汇，定义如下：在直角坐标平面上任意两点
Ax 1 ,y 1 ,Bx 2 ,y 2 的曼哈顿距离为：dA,B =x 1 -x 2 +y -y 1 2 .已知点M在圆O:x2+y2=1上，点N在直
线l:3x+y-9=0上，则dM,N 的最小值为 ( )
9 10 9 10 18-2 10 10
A. B. -1 C. D.3-
10 10 5 3
二、选择题：本题共3小题，每小题6分，共18分。在每小题给出的选项中, 有多项符合题目要求。全部选对
的得6分，部分选对的得3分，有选错的得0分。
9.设集合 P= x0≤x≤4 ,Q= y0≤y≤4 ，则下列图象能表示集合 P到集合Q的函数关系的有
( )
A. B.
C. D.
10.已知二项展开式fx 1 =x3-
x
8 ，下列说法正确的有 ( )
A. fx 的展开式中的常数项是56 B. fx 的展开式中的各项系数之和为0
C. fx 的展开式中的二项式系数最大值是70 D. fi =-16，其中i为虚数单位
11.在△ABC中，若A=nBn∈N* ，则 ( )
A.对任意的n≥2，都有sinA<nsinB B.对任意的n≥2，都有tanA<ntanB
C.存在n，使sinA>nsinB成立 D.存在n，使tanA>ntanB成立
第II卷(非选择题)
三、填空题：本题共3小题，每小题5分，共15分．
12.已知单位向量a,b满足2a+b
= 3，则a-b = .
·6·13.定义两个点集S、T之间的距离集为dS,T = PQ P∈S,Q∈T ，其中PQ 表示两点P、Q之间的距
离，已知k、t∈R，S= x,y y=kx+t,x∈R ，T= x,y y= 4x2+1,x∈R ，若dS,T =1,+∞ ，则t
的值为 .
3
14.已知C:y2= x，过点P1,0
2
倾斜角为60°的直线l交C于A、B两点(A在第一象限内)，过点A作AD⊥
2π
x轴，垂足为D，现将C所在平面以x轴为翻折轴向纸面外翻折，使得∠x -x = ，则几何体
上平面 下平面 3
PABD外接球的表面积为 ．
四、解答题：本题共5小题，共77分。解答应写出文字说明、证明过程或演算步骤。
15（. 13分）已知函数fx =alnx-x．
(1)当a=1时，求函数fx 的单调区间；
(2)当a>0时，求函数fx 的最大值．
16（. 15分）设S n 为数列a n S 的前n项和，已知 n nn+1 1 1 是首项为 、公差为 的等差数列. 2 3
(1)求a n 的通项公式；
2n-1 (2)令b = n a S n，T n 为数列b n
n
n 6n-1 的前n项积，证明：∑T≤ . i 5
i=1
17（. 15分）最新研发的某产品每次试验结果为成功或不成功，且每次试验的成功概率为p(0<p<1)．现对
该产品进行独立重复试验，若试验成功，则试验结束；若试验不成功，则继续试验，且最多试验8次．记X
为试验结束时所进行的试验次数，X的数学期望为EX ．
(1)证明：EX
1
< ；
p
(2)某公司意向投资该产品，若p=0.2，每次试验的成本为a(a>0)元，若试验成功则获利8a元，则该公
司应如何决策投资？请说明理由．
x2 y2 1
18（. 17分）已知椭圆C： + =1(a>0，b>0)的左、右焦点分别为F、F，离心率为 ，经过点F 且倾斜
a2 b2 1 2 2 1
π
角为θ0<θ<
2
的直线l与椭圆交于A、B两点(其中点A在x轴上方)，△ABF 的周长为8．
2
(1)求椭圆C的标准方程；
(2)如图，将平面xOy沿x轴折叠，使y轴正半轴和x轴所确定的半平面(平面AFF)与y轴负半轴和x轴
1 2
所确定的半平面(平面BFF)互相垂直．
1 2
·7·π
①若θ= ，求异面直线AF 和BF 所成角的余弦值；
3 1 2
π
②是否存在θ0<θ<
2
15
，使得折叠后△ABF 的周长为 ？若存在，求tanθ的值；若不存在，请说明理
2 2
由．
19（. 17分）已知定义域为R的函数hx 满足：对于任意的x∈R，都有hx+2π =hx +h2π ，则称函数
hx 具有性质P.
(1)判断函数fx =2x,gx =cosx是否具有性质P；(直接写出结论)
(2)已知函数fx =sinωx+φ
3 5
<ω< ,φ
2 2
π
<
2
，判断是否存在ω,φ，使函数fx 具有性质P？若
存在，求出ω,φ的值；若不存在，说明理由；
(3)设函数fx 具有性质P，且在区间0,2π 上的值域为 f0 ,f2π .函数gx =sin fx ，满足
gx+2π =gx ，且在区间0,2π 上有且只有一个零点.求证：f2π =2π.
·8·江西省上饶市六校 2024 届高三第一次联合考试（2 月）
数学试卷
第I卷(选择题)
一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求
的。
1.已知集合A=x-1≤x≤1 ，B= x y=lg2x-1 ，则A∩B= ( )
A. x-1≤x≤1 B. x0≤x≤1 C. x-1≤x≤0 D. x0<x≤1
4
2.已知复数z= ，其中i为虚数单位，则z= ( )
1-i
A.2+2i B.2-2i C.-2-2i D.-2+2i
3.已知向量a=1,1
，b=m,2
，且a⊥a-b
，则b = ( )
A.2 B.3 C.4 D.2 2
4.曲线fx =ex+ax在点0,1 处的切线与直线y=2x平行，则a= ( )
A.-2 B.-1 C.1 D.2
5.函数fx
xesinx-e-sinx
=
的图象大致为 ( )
ex+e-x
A. B.
C. D.
π 3π
6.若α∈ ,
4 4
π
，6tan +α
4
π
+4cos -α
4
=5cos2α，则sin2α= ( )
24 12 7 1
A. B. C. D.
25 25 25 5
7《. 易·系辞上》有“河出图，洛出书”之说，河图、洛书是中华文化，阴阳术数之源，其中河图排列结构是一、
六在后，二、七在前，三、八在左，四、九在右，五、十背中.如图，白点为阳数，黑点为阴数.若从这10个数中
任取3个数，已知3个数中至多有1个阴数，则取出的3个数之和是5的倍数的概率是 ( )
·9·1 1 1 1
A. B. C. D.
5 4 3 2
4
8.已知圆柱的底面半径为1，高为2，AB，CD分别为上、下底面圆的直径，四面体ABCD的体积为 ，则直
3
线AC与BD所成角的余弦值为 ( )
5 3 2 1
A. B. C. D.
3 3 3 3
二、选择题：本题共3小题，每小题6分，共18分。在每小题给出的选项中, 有多项符合题目要求。全部选对
的得6分，部分选对的得3分，有选错的得0分。
9.已知a>b>0，则 ( )
1 1 1 1
A. < B.2a>2b>1 C.a3<b3 D.log 2<log 2
a b a b
10.已知定义在R上的奇函数fx 满足fx =f2-x ，且fx 在-1,0 上单调递增，则 ( )
A. fx 的图象关于1,0 中心对称 B. fx 是周期函数
C. fx 在1,2
2024
上单调递减 D. fk
k=0
=1
11.已知正项数列a n
1
满足a 1 = 2 ，a n+1 =fa n ，其中fx =lnex-1 -lnx，则 ( )
A. a n 为单调递减数列 B.a <a 2023 2024
1 1
C.a > a D.a +a +a +⋅⋅⋅+a ≥1-
n+1 2 n 1 2 3 n 2n
第II卷(非选择题)
三、填空题：本题共3小题，每小题5分，共15分．
12.请写出一个焦点在y轴上，焦距为4的椭圆的标准方程 .
13.动点P与两个定点O0,0 ，A0,3 满足PA =2PO ，则点P到直线l：mx-y+4-3m=0的距离的最
大值为 .
14.函数fx
π
=2sinωx+
6
π π
(ω>0)在区间 ,
6 2
上有且只有两个零点，则ω的取值范围是 .
四、解答题：本题共5小题，共77分。解答应写出文字说明、证明过程或演算步骤。
15（. 13分）已知某种业公司培育了新品种的软籽石榴，从收获的果实中随机抽取了50个软籽石榴，按质量
(单位：g)将它们分成5组：360,380 ，380,400 ，400,420 ，420,440 ，440,460 ，得到如下频率分布
·10·直方图.
(1)用样本估计总体，求该品种石榴的平均质量；(同一组中的数据用该组区间的中点值作代表)
(2)按分层随机抽样，在样本中，从质量在区间380,400 ，400,420 ，420,440 内的石榴中抽取7个石
榴进行检测，再从中抽取3个石榴作进一步检测.记这3个石榴中质量在区间420,440 内的个数为X，
求X的分布列与数学期望.
16（. 15分）设S n 为数列a n S 的前n项和，已知 n nn+1 1 1 是首项为 、公差为 的等差数列. 2 3
(1)求a n 的通项公式；
2n-1 (2)令b = n a S n，T n 为数列b n
n
n 6n-1 的前n项积，证明：∑T≤ . i 5
i=1
17（. 15分）如图，在四棱锥P-ABCD中，平面PCD⊥平面ABCD，AB⎳CD，AB⊥BC，PD=AB=2CD=
2，BC= 2，∠PDC=120°.
(1)证明：PB⊥AD；
5
(2)点E在线段PC上，当直线AE与平面ABCD所成角的正弦值为 时，求平面ABE与平面PBC的夹
5
角的余弦值.
x2 y2
18（. 17分）已知双曲线C： - =1(a>0，b>0)的左焦点F到其渐近线的距离为 3，点A1,0
a2 b2
在C
上.
(1)求C的标准方程；
(2)若直线l与C交于M，N(不与点A重合)两点，记直线AM，AN，l的斜率分别为k ，k ，k，且kk +kk =
1 2 1 2
-6，是否存在k值，使得FM =FN .若存在，求出k的值和直线l的方程；若不存在，请说明理由.
19（. 17分）若函数 fx 在a,b 上有定义，且对于任意不同的x 1 ,x 2 ∈a,b ，都有 fx 1 -fx 2 <kx 1 -x 2 ，
则称fx 为a,b 上的“k类函数”.
·11·(1)若fx
x2
= +x，判断fx
2
是否为1,2 上的“3类函数”；
(2)若fx =ax-1
x2
ex- -xlnx为1,e
2
上的“2类函数”，求实数a的取值范围；
(3)若fx 为1,2 上的“2类函数”，且f1 =f2 ，证明：∀x 1 ，x 2 ∈1,2 ，fx 1 -fx 2 <1.
·12·A. A 1 ，A 2 互斥 B. PBA 1
5
= 7 C. PA 2 B
1
= D. PB 7
13
= 21
7.阿波罗尼斯(约公元前262年~约公元前190年)，古希腊著名数学家﹐主要著作有《圆锥曲线论》、《论切
触》等.尤其《圆锥曲线论》是一部经典巨著，代表了希腊几何的最高水平，此书集前人之大成，进一步提
出了许多新的性质.其中也包括圆锥曲线的光学性质，光线从双曲线的一个焦点发出，通过双曲线的反
x2 y2
射，反射光线的反向延长线经过其另一个焦点.已知双曲线C： - =1(a>0，b>0)的左、右焦点分
a2 b2
别为F，F，其离心率e= 5，从F 发出的光线经过双曲线C的右支上一点E的反射，反射光线为EP，若
1 2 2
反射光线与入射光线垂直，则sin∠FFE= ( )
2 1
5 5 4 2 5
A. B. C. D.
6 5 5 5
8.若集合 x xlnx+k-ln4 x+k<0 中仅有2个整数，则实数k的取值范围是 ( )
3 4 2
A. ln , ln2
4 3 3
2 3
B. ln2, ln3
3 4
2 3
C. ln2, ln2
3 2
3 2 2
D. ln , ln2
4 3 3
二、选择题：本题共3小题，每小题6分，共18分。在每小题给出的选项中, 有多项符合题目要求。全部选对
的得6分，部分选对的得3分，有选错的得0分。
9.过抛物线y2=2px(p>0)的焦点F作直线l，交抛物线于A,B两点，若FA =3FB ，则直线l的倾斜角可
能为 ( )
A.30° B.60° C.120° D.150°
10.已知函数 fx =asinωx+4φ a>0，ω>0，φ
π
<
3
，若 fx 的图象过A0,1 ，Bm,2 ，Cm+π,0
三点，其中点B为函数fx 图象的最高点(如图所示)，将fx 图象上的每个点的纵坐标保持不变，横坐
1 π
标变为原来的 倍，再向右平移 个单位长度，得到函数gx
4 6
的图象，则 ( )
A. fx
1 5π
=2sin x+
2 6
B. gx
π
=2sin2x-
6
C. fx
2π
的图象关于直线x= 对称 D. gx
3
5π
在 - ,-π
3
上单调递减
11.如图，正方体ABCD-A B C D 的棱长为2，点E是AB的中点，点P为侧面BCC B 内(含边界)一点，则
1 1 1 1 1 1
( )
·14·A.若D P⊥平面A C D，则点P与点B重合
1 1 1
2 6 3π
B.以D为球心， 为半径的球面与截面ACD 的交线的长度为
3 1 3
7 17
C.若P为棱BC中点，则平面D EP截正方体所得截面的面积为
1 6
D.若P到直线A B 的距离与到平面CDD C 的距离相等，则点P的轨迹为一段圆弧
1 1 1 1
第II卷(非选择题)
三、填空题：本题共3小题，每小题5分，共15分．
2
12. x-
x
9
的展开式中的常数项为 ．(用数字作答)．
13.已知A为圆C：x2+y-1
1
2= 上的动点，B为圆E：x-3
4
1 1
2+y2= 上的动点，P为直线y= x上的
4 2
动点，则PB -PA 的最大值为 .
14.在1，3中间插入二者的乘积，得到1，3，3，称数列1，3，3为数列1，3的第一次扩展数列，数列1，3，3，
9，3为数列1，3的第二次扩展数列，重复上述规则，可得1，x ，x ，⋯，x ，3为数列1，3的第n次扩展
1 2 2n-1
数列，令a n =log 3 1×x 1 ×x 2 ×⋯×x 2n-1 ×3 ，则数列a n 的通项公式为 .
四、解答题：本题共5小题，共77分。解答应写出文字说明、证明过程或演算步骤。
15（. 13分）面试是求职者进入职场的一个重要关口，也是机构招聘员工的重要环节.某科技企业招聘员工，
首先要进行笔试，笔试达标者进入面试，面试环节要求应聘者回答3个问题，第一题考查对公司的了解，
答对得2分，答错不得分，第二题和第三题均考查专业知识，每道题答对得4分，答错不得分.
(1)若一共有100人应聘，他们的笔试得分X服从正态分布N60,144 ，规定X≥72为达标，求进入面试
环节的人数大约为多少(结果四舍五入保留整数)；
2 4
(2)某进入面试的应聘者第一题答对的概率为 ，后两题答对的概率均为 ，每道题是否答对互不影响，
3 5
求该应聘者的面试成绩Y的数学期望.
附：若X~Nμ,σ2 (σ>0)，则Pμ-σ<X<μ+σ ≈0.683，Pμ-2σ<X<μ+2σ ≈0.954，
Pμ-3σ<X<μ+3σ ≈0.997.
16（. 15分）如图，在△ABC中，AB=BC=2，D为△ABC外一点，AD=2CD=4，记∠BAD=α，∠BCD=β.
·15·(1)求2cosα-cosβ的值；
(2)若△ABD的面积为S ，△BCD的面积为S ，求S2+S2的最大值.
1 2 1 2
17（. 15分）我国古代数学名著《九章算术》中记载：“刍(chú)甍(méng)者，下有袤有广，而上有袤无广.刍，草
也.甍，窟盖也.”翻译为“底面有长有宽为矩形，顶部只有长没有宽为一条棱.刍甍的字面意思为茅草屋
顶.”现有一个“刍甍”如图所示，四边形ABCD为矩形，四边形ABFE、CDEF为两个全等的等腰梯形，
EF⎳AB，AB=4，EF=AD=2，P是线段AD上一点.
2
(1)若点P是线段AD上靠近点A的三等分点，Q为线段CF上一点，且FQ= FC，证明：PF⎳平面
5
BDQ；
3 2 39
(2)若E到平面ABCD的距离为 ，PF与平面BCF所成角的正弦值为 ，求AP的长.
2 13
x2 y2
18（. 17分）已知椭圆C： a2 + b2 =1(a>b>0)的左、右焦点分别为F 1 ，F 2 ，右顶点为A，且AF 1 +AF 2 =4，
1
离心率为 .
2
(1)求C的方程；
(2)已知点B-1,0 ，M，N是曲线C上两点(点M，N不同于点A)，直线AM,AN分别交直线x=-1于
9
P，Q两点，若BP⋅BQ=- ，证明：直线MN过定点.
4
19（. 17分）已知函数fx =x-1 ex-alnx(a∈R).
(1)当a=e时，求fx 的最小值；
(2)若fx 有2个零点，求a的取值范围.
·16·河南省金太阳联考 2023 - 2024 学年高三上学期 2 月期末检测
数学试题
第I卷(选择题)
一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求
的。
(2+3i)i3
1.已知复数z= ，则z= ( )
1+i
1 5 1 5 1 5 1 5
A.- + i B. + i C.- - i D. - i
2 2 2 2 2 2 2 2
2.已知集合A=x∣log (4-x)<1
2
,B={x∣x>a}，若A∩B=A，则a的最大值是 ( )
A.1 B.2 C.3 D.4
3.“α是第二象限角”是“sinαtanα<0”的 ( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
4.某企业举办冬季趣味运动会，在跳绳比赛中，10名参赛者的成绩(单位：个)分别是152，136，125，131，
129，123，143，119，115，138，则这组数据的中位数是 ( )
A.126 B.129 C.130 D.131
5.已知抛物线C:y2=8x的焦点为F，过点F的直线l与拋物线C交于A，B两点，点A在x轴上方，且A的横
|BF|
坐标为5，则 = ( )
|AF|
2 5 2 3
A. B. ． C. D.
7 7 5 5
6.折纸既是一种玩具，也是一种艺术品，更是一种思维活动．如图，有一张直径为4的圆形纸片，圆心为O，
在圆内任取一点P，折叠纸片，使得圆周上某一点刚好与点P重合，记此时的折痕为l，点Q在l上，则
|OQ|+|PQ|的最小值为 ( )
·17·A.5 B.4 C.3 D.2
x2 y2
7.已知双曲线C: - =1(a>0,b>0)的左焦点为F，过点F的直线l:x+ 3y+m=0与y轴交于点
a2 b2
B，与双曲线C交于点A(A在y轴右侧)．若B是线段AF的中点，则双曲线C的离心率是 ( )
A. 2 B.2 C. 3 D.3
8.函数f(x)=sinx-sin3x+sin2xcosx+2cos3x的值域是 ( )
A.[- 2, 2] B.[-2,2] C.[- 2,2] D.[-2, 2]
二、选择题：本题共3小题，每小题6分，共18分。在每小题给出的选项中, 有多项符合题目要求。全部选对
的得6分，部分选对的得3分，有选错的得0分。
9.设等比数列a n 的前n项和为S ，且S =2n+1+a(a为常数)，则 ( ) n n
A.a=-1 B. a n 的公比为2 C.a =2n D.S =1023 n 9
10.球面三角学是研究球面三角形的边、角关系的一门学科．如图，球O的半径为R,A,B,C为球面上三点，
劣弧BC的弧长记为a，设O 表示以O为圆心，且过B，C的圆，同理，圆O ,O 的劣弧AC，AB的弧长分别
a b c
记为b，c，曲面ABC(阴影部分)叫做曲面三角形，若a=b=c，则称其为曲面等边三角形，线段OA，OB，
OC与曲面△ABC围成的封闭几何体叫做球面三棱堆，记为球面O-ABC．设∠BOC=α,∠AOC=β,
∠AOB=γ，则下列结论正确的是 ( )
·18·3
A.若平面△ABC是面积为 R2的等边三角形，则a=b=c=R
4
B.若a2+b2=c2，则α2+β2=γ2
π 2
C.若a=b=c= R，则球面O-ABC的体积V> R3
3 12
π
D.若平面△ABC为直角三角形，且∠ACB= ，则a2+b2>c2
2
11.已知函数f(x)及其导函数f(x)的定义域均为R，且f(x-1)-f(1-x)=2x-2,f(x)的图象关于点(1,
0)对称，则 ( )
A. f(0)=1 B. y=f(x)-x为偶函数
C. f(x)的图象关于点(1,0)对称 D. f(2024)=-2023
第II卷(非选择题)
三、填空题：本题共3小题，每小题5分，共15分．
12.已知单位向量a,b满足|3a+b|=5，则a⋅(a+2b)=
13.数学中有许多形状优美、寓意独特的几何体，正八面体就是其中之一．正八面体由八个等边三角形构
成，也可以看做由上、下两个正方椎体黏合而成，每个正方椎体由四个三角形与一个正方形组成．如图，
在正八面体ABCDEF中，H是棱BC的中点，则异面直线HF与AC所成角的余弦值是
A
B
H
E
C
D
F
14.将1,2,3,⋯,9这9个数填入如图所示的格子中(要求每个数都要填入，每个格子中只能填一个数)，记第
1行中最大的数为a，第2行中最大的数为b，第3行中最大的数为c，则a<b<c的填法共有 种．
(用数字作答)
·19·第1行
第2行
第3行
四、解答题：本题共5小题，共77分。解答应写出文字说明、证明过程或演算步骤。
15（. 13分）在△ABC中，角A，B，C的对边分别是a，b，c，且tanA+tanC+tanAtanC=1．
(1)求角B的大小；
(2)若b=4，求△ABC面积的最大值．
16（. 15分）某学校组织知识竞赛，题库中试题分A，B两种类型，每个学生选择2题作答，第1题从A，B两种
2
试题中随机选择一题作答，学生若答对第1题，则第2题选择同一种试题作答的概率为 ，若答错第1
3
1 1
题，则第2题选择同一种试题作答的概率为 ．已知学生甲答对A种试题的概率均为 ，答对B种试题
4 2
2
的概率均为 ，且每道试题答对与否相互独立．
3
(1)求学生甲2题均选择B种试题作答的概率；
(2)若学生甲第1题选择A种试题作答，记学生甲答对的试题数为X，求X的分布列与期望．
17（. 15分）如图，在正三棱柱ABC-A B C 中，D，E分别为棱BB ,AB的中点，F在棱CC 上，且EF⎳平面
1 1 1 1 1
ADC ．
1
CF
(1)求 的值；
CC
1
(2)若AA =AB，求平面A EF与平面C EF夹角的余弦值．
1 1 1
x2 y2 3
18（. 17分）已知椭圆C: + =1(a>b>0)的右焦点与点P ,1
a2 b2 2
连线的斜率为2，且点(1,e)在椭圆C
上(其中e为C的离心率)．
(1)求椭圆C的标准方程．
(2)已知点D(2,0)，过点P的直线l与C交于A，B两点，直线DA，DB分别交C于M，N两点，试问直线
MN的斜率是否为定值？若是，求出该定值；若不是，请说明理由．
19（. 17分）已经函数fx =x+a
a
lnx- x2-xa>0
2
．
·20·(1)当a=2时，求曲线y=f(x)在x=1处的切线方程；
1
(2)当0<a< 时，证明：f(x)恰有三个不同的极值点x ,x ,x ，且x x x =1．
2 1 2 3 1 2 3
参考数据：取ln2=0.7．
·21·辽宁省辽东十一所重点高中联合教研体 2024 届高三高考适应
性考试模拟数学试题
第I卷(选择题)
一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求
的。
1.已知集合S=ss=2n+1,n∈Z ，T=tt=4n+1,n∈Z ，则S∩T= ( )
A.∅ B.S C.T D.Z
2.已知复数z满足z =1且有z5+z+1=0，则z= ( )
1 3 1 3 2 2 3 1
A.- ± i B. ± i C. ± i D. ± i
2 2 2 2 2 2 2 2
sinα
3.已知α，β均为锐角，且cos(α+β)= ，则tanα的最大值是 ( )
sinβ
2 2
A.4 B.2 C. D.
4 5
4.为了激发同学们学习数学的热情，某学校开展利用数学知识设计LOGO的比赛，其中某位同学利用函数
图像的一部分设计了如图的LOGO，那么该同学所选的函数最有可能是 ( )
A. fx =x-sinx B. fx =sinx-xcosx
C. fx
1
=x2- D. fx
x2
=sinx+x3
5.如图是古筝鸣箱俯视图，鸣箱有多根弦，每根弦下有一只弦码，弦码又叫雁柱，用于调节音高和传振．图
2是根据图1绘制的古筝弦及其弦码简易直观图．在直观图中，每根弦都垂直于x轴，左边第一根弦在y
轴上，相邻两根弦间的距离为1，弦码所在的曲线(又称为雁柱曲线)方程为y=1.1x，第n(n∈N，第0根
弦表示与y轴重合的弦)根弦分别与雁柱曲线和直线l:y=x+1交于点A nx n ,y n 和B nx n ,y n
20
，则y y n n
n=0
= ( ) 参考数据：1.122=8.14．
A.814 B.900 C.914 D.1000
·22·6.表面积为4π的球内切于圆锥，则该圆锥的表面积的最小值为 ( )
A.4π B.8π C.12π D.16π
7.已知定点P(m,0)，动点Q在圆O：x2+y2=16上，PQ的垂直平分线交直线OQ于M点，若动点M的轨迹
是双曲线，则m的值可以是 ( )
A.2 B.3 C.4 D.5
1
8.设a=cos0.1，b=10sin0.1，c= ，则 ( )
10tan0.1
A.a<b<c B.c<b<a C.c<a<b D.a<c<b
二、选择题：本题共3小题，每小题6分，共18分。在每小题给出的选项中, 有多项符合题目要求。全部选对
的得6分，部分选对的得3分，有选错的得0分。
9.在空间直角坐标系中，有以下两条公认事实：
(1)过点P 0x 0 ,y 0 ,z 0
，且以u=a,b,c abc≠0
x-x y-y
为方向向量的空间直线l的方程为 0 = 0 = a b
z-z
0；
c
(2)过点Px 0 ,y 0 ,z 0
，且v=m,n,t mnt≠0 为法向量的平面α的方程为mx-x 0 +ny-y 0 +
tz-z 0 =0．
现已知平面α:x+2y+3z=6，l 1 : 2 3 x y - -2 y z = = 1 1 ，l 2 :x=y=2-z，l 3 : x- 5 1 = - y 4 = 1 z ( )
A.l ⎳α B.l ⎳α C.l ⎳α D.l ⊥α
1 2 3 1
10.定义：若数列a n 满足，存在实数M，对任意n∈N∗，都有a n ≤M，则称M是数列a n 的一个上界．现已
知a n
a
为正项递增数列，b n = a n-1 n≥2
n
，下列说法正确的是 ( )
A.若a n 有上界，则a n 一定存在最小的上界
B.若a n 有上界，则a n 可能不存在最小的上界
C.若a n
a 1
无上界，则对于任意的n∈N∗，均存在k∈N∗，使得 n < a 2023
n+k
D.若a n 无上界，则存在k∈N∗，当n>k时，恒有b +b +⋯+b <n-2023 2 3 n
11.已知对任意角α，β均有公式sin2α+sin2β=2sinα+β cosα-β .设△ABC的内角A，B，C满足sin2A
+sinA-B+C =sinC-A-B
1
+ .面积S满足1≤S≤2.记a，b，c分别为A，B，C所对的边，则下
2
列式子一定成立的是 ( )
1 a
A.sinAsinBsinC= B.2≤ ≤2 2 C.8≤abc≤16 2 D.bcb+c
4 sinA
>8
第II卷(非选择题)
三、填空题：本题共3小题，每小题5分，共15分．
12.在一个圆周上有8个点，用四条既无公共点又无交点的弦连结它们，则连结方式有 种.
·23·π
13.已知f(x)=2sin2x+
3
3π
，若∃x ,x ,x Î 0,
1 2 3 2
，使得f(x )=f(x )=f(x )，若x +x +x 的最大值为M，
1 2 3 1 2 3
最小值为N，则M+N= .
x2 y2
14.已知椭圆C: + =1，F、F 分别是其左，右焦点，P为椭圆C上非长轴端点的任意一点，D是x轴上
4 3 1 2
S
一点，使得PD平分∠F PF ．过点D作PF 、PF 的垂线，垂足分别为 A、B．则 △DAB 的最大值是
1 2 1 2 S
△PF1F2
．
四、解答题：本题共5小题，共77分。解答应写出文字说明、证明过程或演算步骤。
15（. 13分）近几年，随着生活水平的提高，人们对水果的需求量也随之增加，我市精品水果店大街小巷遍地
开花，其中中华猕猴桃的口感甜酸、可口，风味较好，广受消费者的喜爱.在某水果店，某种猕猴桃整盒出
售，每盒20个.已知各盒含0，1个烂果的概率分别为0.8，0.2.
(1)顾客甲任取一盒，随机检查其中4个猕猴桃，若当中没有烂果，则买下这盒猕猴桃，否则不会购买此种
猕猴桃.求甲购买一盒猕猴桃的概率；
(2)顾客乙第1周网购了一盒这种猕猴桃，若当中没有烂果，则下一周继续网购一盒；若当中有烂果，则隔
一周再网购一盒；以此类推，求乙第5周网购一盒猕猴桃的概率
1
16（. 15分）如图，在直三棱柱ABC-A B C 中，AB=AC，点D在棱AA 上，且A D= AA ,E为A C 的中
1 1 1 1 1 3 1 1 1
点．
(1)证明：平面BDE⊥平面BCC B ；
1 1
(2)若AB=AA =2,BC=2 2,求二面角D-BE-A 的余弦值．
1 1
17（. 15分）记S n 为数列a n 的前n项和，且满足S n =kna n +pa n +qn+rk,p,q,r∈R ．
1
(1)若p=r=0,k= 2 ，求证：数列a n 是等差数列；
(2)若k=q=0,p=2,r≠0，设b n =-1
S
n+1 r n，数列b n 的前n项和为T，若对任意的k∈N*，都有T n 2k-1
<λ<T ，求实数λ的取值范围．
2k
18（. 17分）已知函数fx =ax-ex2,a>0且a≠1.
(1)设gx
fx
=
+ex，讨论gx
x
的单调性；
(2)若a>1且fx 存在三个零点x ,x ,x . 1 2 3
1)求实数a的取值范围；
·24·2e+1
2)设x <x <x ，求证：x +3x +x > .
1 2 3 1 2 3 e
x2 y2
19（. 17分）已知动直线l与椭圆C: 3 + 2 =1交于Px 1 ,y 1 ，Qx 2 ,y 2 两个不同点，且ΔOPQ的面积S = ΔOPQ
6
,其中O为坐标原点.
2
(1)证明x2+x2和y2+y2均为定值;
1 2 1 2
(2)设线段PQ的中点为M，求OM ⋅PQ 的最大值；
6
(3)椭圆C上是否存在点D，E，G，使得S =S =S = ？若存在，判断△DEG的形状；若不存
△ODE △ODG △OEG 2
在，请说明理由.
·25·河北省衡中同卷 2023 - 2024 学年高三 1 月考试
数学试题
第I卷(选择题)
一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求
的。
1.已知集合A=x0≤x≤2 ,B=xx2-x>0 ，则图中的阴影部分表示的集合为 ( )
A. xx≤1 或 x>2 B. xx<0 或1<x<2
C. x1≤x<2 D. x1<x≤2
2.函数fx
4cosx
=
x
的部分图象大致为 ( )
1
+ x2
2
A. B.
C. D.
x2 y2
3.椭圆 + =1a>b>0 a2 b2 的两焦点为F，F，以FF 为边作正三角形，若椭圆恰好平分正三角形的另 1 2 1 2
两条边，则椭圆的离心率为 ( )
1 3
A. B. C.4-2 3 D. 3-1
2 2
4.已知fx =Asinωx+φ A>0,ω>0,φ <π 的一段图像如图所示，则 ( )
·26·A. fx
3π
=sin2x+
4
B. fx
π
的图像的一个对称中心为- ,0
5
C. fx
π 5π
的单调递增区间是 +kπ, +kπ
8 8
,k∈Z
D. fx
5π
的图像向左平移 个单位长度后得到的是一个奇函数的图象
8
5.设a，b，c都是单位向量，且a与b的夹角为60°，则c-a
⋅c-b 的最大值为 ( )
3 3 3 3 3 3
A. - B. + C. - 3 D. + 3
2 2 2 2 2 2
6.在数列{a n }中，a 1 =2，a 2 =1，a n+2 = 2 a a n + , 2 n , 为 n为 偶 奇 数 数 ，则a n
n
的前20项和S = ( ) 20
A.621 B.622 C.1133 D.1134
7.设实数t>0，若te2tx-ln2x ≥0对x>0恒成立，则t的取值范围为 ( )
1
A. ,+∞
2e
1
B. ,+∞
e
1
C. 0,
e
1
D. 0,
2e
x2 y2
8.已知F 1 ，F 2 是双曲线C 1 ： a2 - b2 =1a>0,b>0 的左、右焦点，椭圆C 与双曲线C 的焦点相同，C 与 2 1 1
C 在第一象限的交点为P，若PF 的中点在双曲线C 的渐近线上，且PF ⊥PF ，则椭圆的离心率是
2 1 1 1 2
( )
1 3 5 5
A. B. C. D.
2 2 3 5
二、选择题：本题共3小题，每小题6分，共18分。在每小题给出的选项中, 有多项符合题目要求。全部选对
的得6分，部分选对的得3分，有选错的得0分。
9.已知复数z 0 =1-i，z=x+yix,y∈R ，则下列结论正确的是 ( )
A.方程z-z 0 =2表示的z在复平面内对应点的轨迹是圆
B.方程z-z 0
+z-z 0 =2表示的z在复平面内对应点的轨迹是椭圆
C.方程z-z 0
-z-z 0 =1表示的z在复平面内对应点的轨迹是双曲线的一支
1
D.方程 z+ 2 z 0 +z 0 =z-z 0 表示的z在复平面内对应点的轨迹是抛物线
10.如图，AC为圆锥SO的底面圆O的直径，点B是圆O上异于A，C的动点，SO=OC=2，则下列结论正确
的是 ( )
·27·A.圆锥SO的侧面积为2 2π
8
B.三棱锥S-ABC体积的最大值为
3
π π
C.∠SAB的取值范围是 ,
4 3
D.若AB=BC，E为线段AB上的动点，则SE+CE的最小值为2 3+1
11.如图，曲线y= x下有一系列正三角形，设第n个正三角形Q PQ (Q 为坐标原点)的边长为a ，则
n-1 n n 0 n
( )
2 4
A.a = ,a =
1 3 2 3
B.记S n 为a n
a 3
的前n项和，则P 为S + n+1, a n+1 n 2 2 n+1
C.记S n 为数列a n
3 1
的前n项和，则S = a2 + a n 4 n+1 2 n+1
D.数列a n
2n
的通项公式为a = n 3
第II卷(非选择题)
三、填空题：本题共3小题，每小题5分，共15分．
12.在等比数列a n 中，a 3 ，a 7 是函数fx
1
= x3-4x2+4x-1的极值点，则a = ． 3 5
x2 y2
13.设双曲线Γ： - =1(a>0，b>0)的左、右焦点分别为F 和F，以Γ的实轴为直径的圆记为C，过点
a2 b2 1 2
3
F 作C的切线l，l与Γ的两支分别交于A，B两点，且cos∠FBF= ，则Γ的离心率的值为 .
1 1 2 5
14.如图，对于曲线G所在平面内的点O，若存在以O为顶点的角α，使得对于曲线G上的任意两个不同的
点A,B恒有∠AOB≤α成立，则称角α为曲线G的相对于点O的“界角”，并称其中最小的“界角”为曲线
xex-1+1, x>0
G的相对于点O的“确界角”.已知曲线C：y=
1
(其中e是自然对数的底数)，点O为坐
x2+1, x≤0
16
标原点，曲线C的相对于点O的“确界角”为β，则sinβ= .
·28·四、解答题：本题共5小题，共77分。解答应写出文字说明、证明过程或演算步骤。
15（. 13分）如图所示，在四棱维P-ABCD中，PA⊥面ABCD,AB⊥BC,AB⊥AD，且PA=AB=BC=
1
AD=2.
2
(1)求PB与CD所成的角；
(2)求直线PD与面PAC所成的角的余弦值.
16（. 15分）已知数列a n 满足a =a +2，n∈N∗，且a ，a ，a 构成等比数列. n+1 n 2 5 14
(1)求数列a n 的通项公式；
(2)设b n =2na n+1 ，求数列b n 的前n项和S . n
4S
17（. 15分）在△ABC中，角A,B,C的对边分别为a,b,c,△ABC的面积为S，已知 =a2cosB+abcosA.
tanB
(1)求角B；
S
(2)若b=3,△ABC的周长为l，求 的最大值.
l
x2 y2
18（. 17分）已知椭圆E: + =1a2>7
a2 a2-7
3 3
经过点M-2,
2
.
(1)求E的标准方程；
(2)过点N0,6 的直线l交E于C,D两点(点C在点D的上方)，E的上､下顶点分别为A,B，直线AD与
直线BC交于点Q，证明：点Q在定直线上.
19（. 17分）已知函数fx =x2-ax+2lnx，a∈R．
(1)讨论fx 的单调性；
(2)已知fx 有两个极值点x 1 ,x 2 ，且x 1 <x 2 ，证明：2fx 1 -fx 2 ≥-1-3ln2．
·29·福建省名校联盟全国优质校 2024 届高三大联考
数学试卷
第I卷(选择题)
一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求
的。
1.已知集合A=x2x2-5x+2<0 ，B=xx>1 ，则A∩B= ( )
1
A. 0,
2
1
B. ,1
2
1
C. ,2
2
D. 1,2
1-i
2.已知i为虚数单位，
1-2i
= ( )
5 10 5 2
A. B. C. D.
5 5 2 5
3.已知a，b为单位向量，若a-b
= 3，则a，b的夹角为 ( )
π π 2π 5π
A. B. C. D.
6 3 3 6
4.设直线x-3y+m=0m≠0
x2 y2
与双曲线 - =1(a>b>0)分别交于A、B两点，若线段AB的中点
a2 b2
4
横坐标是 m，则该双曲线的离心率是 ( )
5
5 7
A. B. C.2 D. 2
2 2
5.一般来说，输出信号功率用高斯函数来描述，定义为Ix
(x-μ)2
-
=I e 2σ2 ，其中I 为输出信号功率最大值(单 0 0
位：mW)，x为频率(单位：Hz)，μ为输出信号功率的数学期望，σ2为输出信号的方差，3dB带宽是光通信
中一个常用的指标，是指当输出信号功率下降至最大值一半时，信号的频率范围，即对应函数图象的宽
度。现已知输出信号功率为Ix
(x-2)2
-
=Ie 2 (如图所示)，则其3dB带宽为 ( ) 0
A. ln2 B.4 ln2 C.3 ln2 D.2 2ln2
6.已知a ,a ,a ,a ,a 成等比数列，且2和8为其中的两项，则a 的最小值为 ( )
1 2 3 4 5 5
1 1
A.-32 B.-16 C. D.
32 16
7.如图，在三棱锥P-ABC中，AB=BC= 2,BA⊥BC,PA=PB=PC=2，点M是棱BC上一动点，则PM
+MA的取值范围是 ( )
·30·A. 6+2 7,4 B. 2+ 2,4
10+ 14
C. ,4
2
10+ 14
D. ,2+ 2
2
2014π2
8.方程2cos2x cos2x-cos
x
=cos4x-1所有正根的和为 ( )
A.810π B.1008π C.1080π D.1800π
二、选择题：本题共3小题，每小题6分，共18分。在每小题给出的选项中, 有多项符合题目要求。全部选对
的得6分，部分选对的得3分，有选错的得0分。
9.下列命题正确的是 ( )
A.若A,B两组成对数据的样本相关系数分别为r =0.97,r =-0.99，则A组数据比B组数据的相关性较
A B
强
B.若样本数据x ,x ,⋅⋅⋅,x 的方差为2，则数据2x -1,2x -1,⋅⋅⋅,2x -1的方差为8
1 2 6 1 2 6
C.已知互不相同的30个样本数据，若去掉其中最大和最小的数据，剩下28个数据的22%分位数不等于
原样本数据的22%分位数
D.某人解答5个问题，答对题数为X，若X∼B5,0.6 ，则EX =3
10.对于函数fx
lnx
= ，下列说法正确的是 ( )
x
A. fx
1
在x=e处取得极大值 ； B. fx
e
有两个不同的零点；
C. f4 <fπ <f3 D.π4<4π
11.已知M n 是圆O n :x2+y2-2nx-2ny+n2=0n∈N* 上任意一点，过点P n-1,n 向圆O 引斜率为k n n
k n >0 的切线l n ，切点为Q nx n ,y n ，点A n3n,n ，则下列说法正确的是 ( )
n 2n+1
A.n=1时，k = 3 B. y = +n
1 n n+1
1-x x
C. n < 2sin n 1+x y -n
n n
1
D. 2 M n A n +M n P n
3
的最小值是 n+1 2
第II卷(非选择题)
三、填空题：本题共3小题，每小题5分，共15分．
12.设S n 是数列a n
S S
的前n项和， n+1 - n =1，a =5，则a = ． n+1 n 3 2024
13.设函数fx
π
=sinωx+
3
(ω>0)在区间0,π 恰有两个零点，则ω的取值范围是 ．
·31·14.如图，在△SBE中，SE=BE=1，在直角梯形BEDC中，BE⊥DE，CD∥BE，CD=2，DE= 3，DE⊥
π 2π
SE，记二面角S-DE-B的大小为θ，若θ∈ ,
3 3
，则直线SC与平面SDE所成角的正弦值的最大值
为 ．
四、解答题：本题共5小题，共77分。解答应写出文字说明、证明过程或演算步骤。
15（. 13分）若数列a n 的前n项和S 满足S =2a +n-4． n n n
(1)证明：数列a -1
n
是等比数列；
(2)设b n =log 2a n+1 -1 ，求数列 b na n -1 的前n项和T． n
16（. 15分）在三棱柱ABC-A B C 中，AA =13，在底面△ABC中，有AB⊥BC，且AB=8，BC=6，点D为
1 1 1 1
12
等腰三角形B AC的底边AC的中点，在△BB D中，有cos∠BB D= ．
1 1 1 13
(1)求证：BC⊥B D；
1
(2)求直线AB 与平面B BC所成角的正弦值．
1 1
17（. 15分）甲、乙两俱乐部进行羽毛球团体赛，比赛依次按照男子双打、女子双打、混合双打、男子单打、女子
单打共五个项目进行，规定每个项目均采取三局两胜制，且在上述五项中率先赢下三项的俱乐部获胜
(后续项目不再进行比赛)．已知在男双项目、女双项目、男单项目这三项的每局中，甲俱乐部获胜的概率
均为0.7；在混双项目、女单项目这两项的每局中，乙俱乐部获胜的概率均为0.8，假设每局比赛之间互不
影响．(注：比赛没有平局，且所有结果均保留一位小数．)
(1)求甲俱乐部在男子双打项目中获胜的概率；
(2)记比赛结束时所完成的比赛项目数量为随机变量X，求X的分布列和数学期望．
x2 y2
18（. 17分）已知椭圆E的方程为 + =1(a>b>0),A为E的左顶点，B为E的上顶点，E的离心率为
a2 b2
1
,△ABO的面积为 3．
2
(1)求E的方程；
·32·(2)过点P-2,1 的直线交E于M、N两点，过点M且垂直于x轴的直线交直线AN于点H，证明：线段
MH的中点在定直线上．
19（. 17分）已知函数fx
a
=lnx- ．
x
(1)当a=-1时，求fx 的极值；
1
(2)若存在实数0<x 0 < 2 ，满足fx 0
x2
=f 0 1-x
0
，求fa2 的取值范围．
·33·浙江省名校协作体 2024 届高三下学期开学适应性考试
数学试题
第I卷(选择题)
一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求
的。
1.已知集合M=x∣x2-3x-4<0 ,N={x∣y=ln(x-1)}，则M∩N= ( )
A.(1,4) B.[1,4) C.(-1,4) D.[-1,4)
2.若1-2i z-3-2i
=2+i，则z= ( )
A.-3+3i B.-3-3i C.3+3i D.3-3i
x2 y2
3.已知直线ax+y=0是双曲线 - =1(a>0)的一条渐近线，则该双曲线的半焦距为 ( )
a2 4
A. 6 B.2 6 C.2 2 D.4 2
4.已知a,b是两个不共线的单位向量，向量c=λa+μb(λ,μ∈R)．“λ>0，且μ>0”是“c⋅(a+b)>0”的
( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
5.函数fx =alnx
1
+ 的图象不可能是 ( )
x
A. B.
C. D.
6.如图，将正四棱台切割成九个部分，其中一个部分为长方体，四个部分为直三棱柱，四个部分为四棱锥．
已知每个直三棱柱的体积为3，每个四棱锥的体积为1，则该正四棱台的体积为 ( )
·34·A.36 B.32 C.28 D.24
7.在平面直角坐标系xOy中，圆C的方程为x-3 2+y2=1，且圆C与x轴交于M,N两点，设直线l的方程
为y=kxk>0 ，直线l与圆C相交于A,B两点，直线AM与直线BN相交于点P，直线AM、直线BN、直
线OP的斜率分别为k ,k ,k ，则 ( )
1 2 3
A.k +k =2k B.2k +k =k C.k +2k =k D.k +k =k
1 2 3 1 2 3 1 2 3 1 2 3
8.已知直线BC垂直单位圆O所在的平面，且直线BC交单位圆于点A，AB=BC=1，P为单位圆上除A外
的任意一点，l为过点P的单位圆O的切线，则 ( )
A.有且仅有一点P使二面角B-l-C取得最小值
B.有且仅有两点P使二面角B-l-C取得最小值
C.有且仅有一点P使二面角B-l-C取得最大值
D.有且仅有两点P使二面角B-l-C取得最大值
二、选择题：本题共3小题，每小题6分，共18分。在每小题给出的选项中, 有多项符合题目要求。全部选对
的得6分，部分选对的得3分，有选错的得0分。
9.一个盒子里装有除颜色外完全相同的四个小球，其中黑球有两个，编号为1，2；红球有两个，编号为3，4，
从中不放回的依次取出两个球，A表示事件“取出的两球不同色”，B表示事件“第一次取出的是黑球”，
C表示事件“第二次取出的是黑球”，D表示事件“取出的两球同色”，则 ( )
A. A与D相互独立. B. A与B相互独立 C. B与D相互独立 D. A与C相互独立
10.已知函数fx ，gx 的定义域均为R，且fx +g2-x =5，gx -fx-4 =7．若x=2是gx 的对
称轴，且g2 =4，则下列结论正确的是 ( )
A. fx 是奇函数 B. 3,6 是gx 的对称中心
C.2是fx
22
的周期 D.gk
k=1
=130
11.在平面直角坐标系中，将函数 f(x)的图象绕坐标原点逆时针旋转α(0<α≤90°)后，所得曲线仍然是某
个函数的图象，则称f(x)为“α旋转函数”.那么 ( )
A.存在90°旋转函数 B.80°旋转函数一定是70°旋转函数
1 bx
C.若g(x)=ax+ 为45°旋转函数，则a=1 D.若h(x)= 为45°旋转函数，则-e2≤b≤0
x ex
第II卷(非选择题)
·35·三、填空题：本题共3小题，每小题5分，共15分．
x
12.2+
y
x-2y 6的展开式中x4y2的系数为 ．(用数字作答)
13.已知F为抛物线C:y2=4x的焦点，直线x=t与C交于A，B，AF与C的另一个交点为D，BF与C的另一
个交点为E.若△ABF与△DEF的面积之比为4:1，则t= .
14.设严格递增的整数数列a ，a ，⋯，a 满足a =1，a =40.设f为a +a ，a +a ，⋯，a +a 这19个数中
1 2 20 1 20 1 2 2 3 19 20
被3整除的项的个数，则f的最大值为 ，使得f取到最大值的数列a n 的个数为 .
四、解答题：本题共5小题，共77分。解答应写出文字说明、证明过程或演算步骤。
15（. 13分）如图，在三棱锥A-BCD中，AB⊥平面BCD，平面ABC⊥平面ABD，AC=AD，AB=BD.
(1)证明：BC⊥BD；
(2)求二面角A-CD-B的余弦值.
π
16（. 15分）记△ABC的内角A，B，C的对边分别为a，b，c，已知A= ，a=2.
3
(1)若sinB+sinC=2sinA，求△ABC的面积；
3
(2)若sinB-sinC= ，求b.
4
π
17（. 15分）设0<x< .
2
1 cos4x-4cos2x+3
(1)若tanx= ，求 ；
2 cos4x+4cos2x+3
tanx-x
(2)证明： >2；
x-sinx
(3)若tanx+2sinx-ax>0，求实数a的取值范围.
18（. 17分）设离散型随机变量X和Y有相同的可能取值，它们的分布列分别为PX=a k =x k ，PY=a k =
n n
y ，x >0，y >0，k=1,2,⋯,n,x =y =1．指标D(X‖Y)可用来刻画X和Y的相似程度，其定义为
k k k k k
k=1 k=1
n x
D(X‖Y)=x ln k．设X~B(n,p),0<p<1．
k y
k=1 k
(1)若Y~B(n,q),0<q<1，求D(X‖Y)；
1
(2)若n=2,P(Y=k-1)= ,k=1,2,3，求D(X‖Y)的最小值；
3
(3)对任意与X有相同可能取值的随机变量Y，证明：D(X‖Y)≥0，并指出取等号的充要条件
x2 y2 x2+4x y2
19（. 17分）已知椭圆C： + =1的左焦点为F，P为曲线E： + =0上的动点，且点P不在x
25 9 25 9
·36·轴上，直线FP交C于A，B两点.
(1)证明：曲线E为椭圆，并求其离心率；
(2)证明：P为线段AB的中点；
(3)设过点A，B且与AB垂直的直线与C的另一个交点分别为M，N，求△PMN面积的取值范围.
·37·2024 年 2 月第二届“鱼塘杯”高考适应性练习
数学试题
第I卷(选择题)
一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求
的。
1.设复数z=1+i,w=3+2i，则z+w的虚部是 ( )
A.-3 B.3 C.-3i D.3i
2.如果可导曲线y=fx 在点 x 0 ,fx 0 的切线方程为x+eay-3=0，其中a∈R，则 ( )
A. f x 0 >0 B. f x 0 =0 C. f x 0 <0 D.无法确定
3.设锐角α满足tanα∈0,1 ，则数据sinα,cosα,sinπ-α ,cosα+π 的极差是 ( )
π
A.2sinα B.2cosα C. 2sinα-
4
π
D.- 2sinα-
4
x2 x2
4.设焦距相同的椭圆C : +y2=1和双曲线C : -y2=1(a>0)相交于分别位于第一象限､第二象限的
1 4 2 a2
A,B两点，两圆锥曲线的公共左焦点为F，则|FA|2-|FB|2的值是 ( )
A. 2 B.2 2 C.4 2 D.8 2
5.已知公比q与首项a 1 均不为0的等比数列a n ，则“a n 单调递增”是“q>1”的 ( )
A.充要条件 B.充分不必要条件 C.必要不充分条件 D.既不充分也不必要条件
6.已知三棱锥P-ABC底面△ABC为边长为2的等边三角形，O是底面ABC上一点，三棱锥体积V =
P-ABC
3.则对∀μ,λ∈R,OP+μOA+λOB 的最小值是 ( )
3
A.1 B.3 C. 3 D.
3
x2 y2
7.设椭圆 25 + 16 =1的左､右焦点为F 1 ,F 2 ，椭圆上一点P和平面一点F满足PF=4F 2 P，则F 1 F 的最大
值与最小值之和是 ( )
A.48 B.50 C.52 D.54
8.已知 fx 是定义在0,+∞ 上单调递增且图像连续不断的函数，且有 fx+y
fx
=
+fy
1+fx fy ，设x > 1
x >1，则下列说法正确的是 ( )
2
A. fx 1 +fx 2 x +x >f 1 2
2 2
>1 B.1> fx 1 +fx 2 x +x >f 1 2
2 2
x +x C. f 1 2
2
> fx 1 +fx 2 x +x >1 D.1>f 1 2
2 2
> fx 1 +fx 2
2
二、选择题：本题共3小题，每小题6分，共18分。在每小题给出的选项中, 有多项符合题目要求。全部选对
·38·的得6分，部分选对的得3分，有选错的得0分。
9.对于一个随机试验，设Ω是样本空间，A是随机事件，ω是样本点，则下列说法正确的是 ( )
A. A∈Ω B. A⊆Ω C.ω∈Ω D.ω⊆Ω
10.设全集为U，设A,B是两个集合，定义集合TA,B = A∩∁ U B ∪ B∩∁ U A ，则下列说法正确的是
( )
A.TA,A =∅ B.T∅,A =A C.TA,U =A D.TA,B =TB,A
11.已知定义域为0,+∞ 的函数 fx =cosπx +sin πx x ，其中 x 代表不超过x的最大整数.设数列
a n 满足：a n 是fx 在2n,2n+2 上最大值，数列x n 满足：fx n =a n 且x n ∈2n,2n+2 ，则下列说法
正确的是 ( )
A. fx 最小值为-2 B. fx 在2n,2n+2 有4n+2个极值点
1
C. x ∈2n,2n+
n 4n
π
D.a >cos +1
n 4n
第II卷(非选择题)
三、填空题：本题共3小题，每小题5分，共15分．
12.若底面边长为2的正六棱柱存在内切球，则其外接球体积是 .
13.小鱼和A，B，C，D，E共六个好友在圆桌上用餐，则A坐在小鱼对面且B和C不相对的坐法的种数是
.如果圆桌可以旋转后重合，则记为同一种排列方式.
m
14.如果X,Y是离散型随机变量，则X在Y=y事件下的期望满足E(X∣Y=y)=x i PX=x i ∣Y=y
i=1
其中
x ,x ,⋯,x
1 2 m
是X所有可能取值的集合.已知某独立重复试验的成功概率为p，进行n次试验，求第n次
试验恰好是第二次成功的条件下，第一次成功的试验次数X的数学期望是 .
四、解答题：本题共5小题，共77分。解答应写出文字说明、证明过程或演算步骤。
15.(13分)
设数列a n ,b n 满足：a =2,b =3，且4a -b =a -3b ,4b -2b =2a -3a 对n∈N*成立. 1 1 n+1 n n n+1 n+1 n n n+1
(1)证明：a +b
n n
是等比数列；
(2)求a n 和b n 的通项公式.
16.(15分)
在四面体PABC中，M为AB中点，O为PABC外接球的球心，且AC⊥BC,|AP|2+|BP|2=2,|PC|=1.
(1)证明：PO⊥CM；
(2)若PO =1，求四面体PCOM体积的最大值.
17.(15分)
1
设△ABC的外接圆半径是 ,A,C均为锐角，且|AC|=|AB|2+|BC|2.
2
·39·(1)证明：△ABC不是锐角三角形；
(2)证明：在△ABC的外接圆上存在唯一的一点D，满足对平面上任意一点P，有|PA|2-|PB|2=|PD|2
-|PC|2.
18.(17分)
已知抛物线C:y2=2px(p>0)的焦点F,F关于原点的对称点是M,⊙M为M为圆心，OM =1为半径的
圆.直线l是过⊙M上异于原点的一点A的C的切线，切点为T.
(1)求FT 的最大值；
FA
(2)求
FT
的最大值.
19.(17分)
请在下列题目中任选一题作答，将选择题目的序号(粗体大写英文字母)写在答题卡醒目位置.如果选择
多题，则按所选择的第一题计分.
(A)．
称I⊆Z是Z的一个向往集合，当且仅当其满足如下两条性质：(1)任意a,b∈I，a+b∈I；(2)任意a∈I
和c∈Z，有ca∈I.任取a ,a ,⋯,a ∈Z，称包含a ,a ,⋯,a 的最小向往集合称为a ,a ,⋯,a 的生成向往集
1 2 n 1 2 n 1 2 n
合，记为a 1 ,a 2 ,⋯,a n .
(1)求满足6,8 =x 的正整数x的值；
(2)对两个向往集合I 1 ,I 2 ，定义集合SI 1 ,I 2 =a+b∣a∈I,b∈I 1 2 ,PI 1 ,I 2 =
a b +a b +⋯+a b ∣a ,a ,⋯,a ∈I,b ,b ,⋯,b ∈I,n=1,2,⋯
1 1 2 2 n n 1 2 n 1 1 2 n 2
.
(i)证明：P 4,6 ,3 仍然是向往集合，并求正整数x，满足P 4,6 ,3 =x ；
(ii)证明：如果SI 1 ,I 2 =Z，则I 1 ∩I 2 =PI 1 ,I 2 .
(B)．
对三次函数fx
b
=ax2+bx2+cx+d,a≠0，如果其存在三个实根x ,x ,x ，则有x +x +x =- ,x x +x x 1 2 3 1 2 3 a 1 2 2 3
c d
+x x = ,x x x =- .称为三次方程根与系数关系.
3 1 a 1 2 3 a
(1)对三次函数fx =ax2+bx2+cx+d，设gx =f x ，存在x 0 ∈R，满足0=fx 0 =gx 0 ≠g x 0 .证
明：存在x 1 ≠x 0 ，使得fx =ax-x 1 x-x 0 2；
(2)称fx 是m,M 上的广义正弦函数当且仅当fx 存在极值点x 1 ,x 2 ∈m,M ，使得 fx 1 ,fx 2 =
fm ,fM .在平面直角坐标系xOy中，Aa,b 是第一象限上一点，设fx =xa-x
b
+ ,gx
x
=
x(a-x)2-4b.已知gx 在0,a 上有两根x <x . 0 3
(i)证明：fx 在0,+∞ 上存在两个极值点的充要条件是a3>27b；
(ii)求点A组成的点集，满足fx 是x 0 ,x 3 上的广义正弦函数.
(C)．
·40·设有两个集合A,B，如果对任意a∈A，存在唯一的b∈B，满足fa =b，那么称f是一个A→B的函数.
设fa 是A→B的函数，gb 是B→C的函数，那么g fa 是A→C的函数，称为g和f的复合，记为g
∘f.如果两个A→B的函数f,g对任意a∈A，都有fa =ga ，则称f=g.
(1)对fx =ex2，分别求一个gx ,hx ，使得g∘f x =x=f∘h x 对全体x≥1恒成立；
(2)设集合A,B,C和A→C的函数α以及B→C的函数β.
(i)对E= a,b ∣a∈A,b∈B,αa =βb ，构造E→A的函数p以及E→B的函数q，满足α∘p=β∘q；
(ii)对E= a,b ∣a∈A,b∈B,αa =βb ，构造E→A的函数p以及E→B的函数q，满足α∘p=β∘q，
并且如果存在其它的集合E满足存在E→A的函数p以及E→B的函数q，满足α∘p=β∘q，则存在唯
一的E→E的函数ψ满足p∘ψ=p,q∘ψ=q.
(D)．
对集合E，定义其特征函数X Ex
1,x∈E,
= 0,x∉E. 考虑集合E 1 ,E 2 ,⋯,E n 和正实数a 1 ,a 2 ,⋯,a n ，定义S a,E (x)=
n
a i X Ei (x)为L和式函数.设E i =m i ,M i
i=1
，则E ,E ,⋯,E 为闭区间列；如果集合E ,E ,⋯,E 对任意1≤i 1 2 n 1 2 n
<j≤n，有E i ∩E j =∅，则称E 1 ,⋯,E n 是无交集合列，设集合P nE =E ∪E ∪⋯∪E . 1 2 n
(1)证明：L和式函数的值域为有限集合；
(2)设E 1 ,E 2 ,⋯,E n 为闭区间列，S a,Ex 是定义在P nE 上的函数.已知存在唯一的正整数m，各项不同的
非零实数c 1 ,c 2 ,⋯,c m ，和无交集合列F 1 ,F 2 ,⋯,F m 使得P mF =P nE
m m
，并且cX (x)=S (x)，称cX i Fi a,E i Fi
i=1 i=1
(x)为L和式函数S a,Ex 的典范形式.设m为S a,Ex 的典范数.
(i)设m <M <m <M <⋯<m <M ，证明：m≤n；
1 1 2 2 n n
(ii)给定正整数n，任取正实数a 1 ,a 2 ,⋯,a n 和闭区间列E 1 ,E 2 ,⋯,E n ，判断S a,Ex 的典范数m最大值的存在
性.如果存在，给出最大值；如果不存在，说明理由.
·41·湖北省新高考联考协作体 2023-2024 学年高三下学期 2 月收心
考试数学试卷
第I卷(选择题)
一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求
的。
1.已知A=x∈R∣log (x-1)<1
2
,B=y∣y=2x,x∈A , 则A∩B等于 ( )
A.⌀ B.{x∣2<x<3} C.{x∣1<x<8} D.{x∣1<x<3}
2.已知复数z满足|z|⋅z=2 3-2i, 则复数z在复平面内对应的点位于 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.已知抛物线C的顶点在原点, 焦点F在坐标轴上, 点F关于其准线的对称点为(6,0), 则C的方程为
( )
A. y2=-8x B. y2=-4x C. y2=8x D. y2=4x
4.某公司为激励创新, 计划逐年加大研发资金投入. 若该公司2023年全年投入研发资金160万元, 在此基
础上，每年投入的研发资金比上一年增长10% ，则该公司全年投入的研发资金开始超过200万元的年份
是 ( ) (参考数据:lg1.1≈0.04,lg2≈0.30)
A.2024年 B.2025年 C.2026年 D.2027年
5.已知e是单位向量, 且|2e-a|= 10,a+2e在e上的投影向量为5e, 则a与e的夹角为 ( )
π π π 5π
A. B. C. D.
6 4 3 12
2x-8x
6.已知函数f(x)= (a>0且a≠1)是偶函数, 则a= ( )
x⋅ax
1 1
A. B. C.2 D.4
2 4
3
7.已知圆C:x2+y2-2x=0, 过圆C外一点P作圆的两条切找, 切点分别为A,B, 三角形PAB的面积为 ,
12
则PC的长为 ( )
3 2 3
A. B. C. 3 D.2
3 3
8. 已知数列 a n 是等比数列, 则 存在正整数 k, 对于 ∀t∈N*,a t >a t+k 恒成立”是: a n 为递减数列”
的 ( )
A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分也不必要条件
二、选择题：本题共3小题，每小题6分，共18分。在每小题给出的选项中, 有多项符合题目要求。全部选对
的得6分，部分选对的得3分，有选错的得0分。
·42·9. 中国古代数学的瑰宝《九章算术》中记载了一种称为 曲池”的几何体, 该几何体是上、下底面均为扇环
形的柱体 (扇环是指圆环被扇形截得的部分) . 现有一个如图所示的曲池, AA 垂直于底面, AA =5, 底
1 1
π
面扇环所对的圆心角为 , 弧 AD 的长度是弧 BC 长度的 3 倍, CD=2, 则下列说法正确的是
2
( )
3 10π
A.弧 AD 长度为 π B.曲池的体积为
2 3
C.曲池的表面积为 20+14π D.三棱锥 A-CC D 的体积为 5
1
3
10.设函数f(x)=log x3-3ax(a>0且a≠1)在区间 ,2
a 2
上单调递减, 则a的取值可以为 ( )
2 3 4
A. B. C. D.3
2 2 3
11.数列a n 共有11项, 前11项和为S 11 , 且满足a n+1 -a n 2=3a n+1 -a n -2,a =1, 则下列说法正确的是 1
( )
A. a n 可以是等差数列
B. a n 可以不是等差数列
C.所有符合已知条件的数列a n 中, S 的取值个数为55 11
D.符合已知条件且满足2a 6 =a 1 +a 11 的数列a n 的个数为252
第II卷(非选择题)
三、填空题：本题共3小题，每小题5分，共15分．
12.已知a,b是不同的直线，α,β是不同的平面，则下列四个结论：
(1)若a∥α,a∥β, 则α∥β ：
(2)若a∥b,a∥α, 则b∥α:
(3)若a⏊α,a⏊β, 则α∥β ；
(4)若α⏊β,a∥α, 则a⏊β:
以上结论中，正确的序号是 ．
13.如图, 圆和直角梯形 ABCD, 其中 AD∥BC,AB⏊BC,AD=4,AB=6,BC=8, 且 A,C,D 三点在圆上,
则圆的面积为 ．
·43·A B
D
C
14.将函数 f(x)=2sinx-1的图象上所有点的横坐标不变纵坐标伸长为原来的2倍, 向下平移1个单位长
度, 向左平移φ(φ∈(0,π])个单位长度, 最后所有点的纵坐标不变横坐标压缩到原来的0.5倍,得到函数
π
g(x)的图象. 若对任意x ∈ 0, 1 2
π
, 都存在x ∈ - ,0 2 4 , 使得 f x 1 =gx 2 , 则φ的取值范围为
．
四、解答题：本题共5小题，共77分。解答应写出文字说明、证明过程或演算步骤。
cosB
15（. 13分）记△ABC的内角A,B,C的对边分别为a,b,c, 已知 =tanC
1+sinB
π
(1)若C= , 求B;
6
7
(2)荐b= c, 求sinC的值.
2
16. (15分)已知盒中有4个黑球和2个白球, 每次从盒中不放回的随机摸取1个球, 直到盒中剩下的球颜
色相同就停止摸球
(1)求摸球两次后就停止摸球的概率;
(2)记摸球的次数为随机变量X, 求X的分布列和期望.
17. (15分)如图, 在叫棱锥P-ABCD中, 底面ABCD为菱形, PA⫫底面ABCD,PA=AB=2, BD=2 3,E
1
为线段PB的中点, DF= DC, 点G在线段PC上(不含端点), 再从下面三个条件中选择一个条件作
4
为已知条件.
①A、E、G、F四点共面；②AG⏊平面PBD；③EG⎳平面PAF
PG
(1)求 的值;
PC
(2)求平面AEG与平面APF所成角的余弦值.
x2 y2
18. (17 分) 已知椭圆 C: + =1(a>b>0) 长轴的左右顶点分别为 A ,A , 短轴的上下顶点分别为
a2 b2 1 2
·44·3
B ,B , 四边形 A B A B 面积为 4 , 椭圆 C 的离心率是 .
1 2 1 1 2 2 2
y
B
1
T
P
x
A 1 O Q A 2 M
B N
2
(1)求C 的方程;
(2)过点T(2,1)的直线交 C 于 P,Q两点, 直线 B P,B Q与直线 y=-1的交点分別为 M,N, 证明:线段
1 1
MN 的中点为定点.
ex
19（. 17分）函数f(x)= x -a图像与x轴的两交点为Ax 1 ,0 ,Bx 2 ,0 x 2 >x 1
(1)令h(x)=f(x)-lnx+x, 若h(x)有两个零点, 求实数a的取值范围；
(2)证明:x x <1:
1 2
3
(3)证明:当a≥5时, 以AB为直径的圆与直线y= (x+1)恒有公共点．
4
(参考数据：e0.25≈1.3,e2.5≈12.2)
·45·安徽省部分学校 2023 - 2024 学年高三下学期春季阶段性检测
数学试题
第I卷(选择题)
一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求
的。
1.已知集合M=xx2-4>0 和N=x-3<x<1 ，则∁ R M ∩N= ( )
A.(-3,-2) B.(-2,1) C.[-2,1) D.(-∞,1)∪(2,+∞)
5i
2.复数z= 在复平面内对应的点位于 ( )
1-2i
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.已知非零向量a，b满足a⊥b，设甲：a
=b
，乙：2a-b
=2b+a ，则 ( )
A.甲是乙的充要条件 B.甲是乙的充分条件但不是必要条件
C.甲是乙的必要条件但不是充分条件 D.甲既不是乙的充分条件也不是乙的必要条件
4.某研究机构通过统计分析发现，教师的工作效率E与工作年数r(r>0)、劳累程度T(0<T<1)有关，并
建立了数学模型E=10-10T⋅2-0.14r，已知李老师工作了20年，根据上述公式，与工作10年时相比，如果
他的工作效率不变，则他现在的劳累程度是工作10年时劳累程度的 ( )
A.2-2.8倍 B.21.4倍 C.22.8倍 D.25.6倍
5.已知数列a n 中，a =1，a =3，且当n>2时，a =a -a ，则a = ( ) 1 15 n n-1 n-2 2
A.-4 B.-3 C.3 D.4
6.设△ABC的内角A，B，C的对边分别为a，b，c，已知b= 13c，D为边BC上一点，CD=2BD=2，AD=
3，则△ABC的面积为 ( )
3 3 3 3 3 3
A. B. C. D.
4 4 4 2
π
7.已知抛物线C:y2=2px(p>0)，过C的焦点F且倾斜角为 的直线交C于A，B两点，线段AB的中点为
3
4
W，|FW|= ，则p= ( )
3
A.1 B.2 C.3 D.4
1
8.设a=ln1.01，b= ，c=tan0.01，则 ( )
101
A.a<b<c B.a<c<b C.b<c<a D.b<a<c
二、选择题：本题共3小题，每小题6分，共18分。在每小题给出的选项中, 有多项符合题目要求。全部选对
的得6分，部分选对的得3分，有选错的得0分。
·46·9.某专业饲料市场研究机构统计得到2023年1-9月和2022年同期的豆粕价格走势图如图所示，则
( )
A.2023年1-9月的豆粕价格仅有4个月低于2022年同期
B.从极差来看，2022年1-9月的豆粕价格比2023年同期波动范围更大
C.2023年1-9月的豆粕价格的中位数为2.30
D.2022年1-9月的豆粕价格的平均数低于2.30
10.如图，在平行六面体ABCD-A B C D 中，底面ABCD为正方形，平面ABCD⊥平面ABB A ，△A AB是
1 1 1 1 1 1 1
边长为2的等边三角形，M,N分别是线段A B，DB 的中点，则 ( )
1 1
A. A B⊥B D B.MN⎳平面ABCD
1 1
6 3
C. B C与A B所成角的余弦值为 D. B D与平面ABCD所成角的正弦值为
1 1 4 1 4
x2 y2
11.已知椭圆E: + =1(a>b>0)的左、右焦点分别为F，F，左、右顶点分别为A，B，上顶点为D，P是
a2 b2 1 2
E上异于A，B的一个动点，若 AF 1
BF 1
=7-4 3，则 ( )
3 1
A. E的离心率为 B.直线PA与PB的斜率之积为-
2 2
C.满足PF ⋅PF =0的点P有4个 D.|PD|<2 2b
1 2
第II卷(非选择题)
三、填空题：本题共3小题，每小题5分，共15分．
12.若f(x)=x3+(a-1)cosx+asinx为奇函数，则曲线y=f(x)在点(0,f(0))处的切线方程为 .
13.某商场搞抽奖活动，将30副甲品牌耳机和20副乙品牌耳机放入抽奖箱中，让顾客从中随机抽1副，两个
·47·品牌的耳机外包装相同，耳机的颜色都只有黑色和白色，记事件A=“抽到白色耳机”，B=“抽到乙品牌
3 3
耳机”，若P(A∣B)= ，P(B∣A)= ，则抽奖箱中甲品牌的黑色耳机有 副.
4 7
14.若正四面体ABCD的顶点都在一个表面积为6π的球面上，过点C且与BD平行的平面α分别与棱AB,
AD交于点E,F，则空间四边形BCFE的四条边长之和的最小值为 .
四、解答题：本题共5小题，共77分。解答应写出文字说明、证明过程或演算步骤。
15（. 13分）某大棚种植户通过长期观察统计，发现去年本地市场中黄瓜每天的收购价格X(元/kg)服从正态
分布N(4,1)，规定收购价格在(3,6)内的为“合理价格”.
(1)从去年随机抽取10天，记这10天中黄瓜的收购价格是“合理价格”的天数为Y，求E(Y)；
(2)该大棚种植户为家乡的农产品做了5次直播带货，成交额y(万元)如下表所示：
第x次直播带货 1 2 3 4 5
成交额y(万元) 9 12 17 21 27
若用最小二乘法得到的y关于x的线性回归方程为y=bx+3.7，预计该大棚种植户第7次直播带货的成
交额为多少万元.
附：若X~Nμ,σ2 ，则P(μ-σ<X<μ+σ)=0.6827，P(μ-2σ<X<μ+2σ)=0.9545.
16（. 15分）如图，等边三角形ABC与正方形BCC B 所在平面垂直，且AB=2，AG⎳BB ，CB 与BC 的交点
1 1 1 1 1
为D，AD⎳平面GB C .
1 1
(1)求线段AG的长度；
(2)求平面BC G与平面GB C 夹角的余弦值.
1 1 1
17（. 15分）已知等差数列a n 的前n项和为S n ，a n ≠0，a n a n+1 =2S n ，b n 是各项均为正数的等比数列，b +b 7 8
=8b 4 +b 5 ，且b =2. 1
(1)求a n 和b n 的通项公式；
1
a
a
,n为奇数
(2)设c n = a n n+2 ，数列c n
n,n为偶数
b
n
25
的前n项和为T，证明：T < . n 2n 18
x2 y2
18（. 17分）已知双曲线C: - =1(a>0，b>0)的左顶点为A(-2,0)，过点H(4,0)的动直线l交C于P，
a2 b2
Q两点(均不与A重合)，当l与x轴垂直时，|PQ|=6.
(1)求C的方程；
(2)若直线AP和AQ分别与直线x=-4交于点M和N，证明：MH⋅NH为定值.
·48·19（. 17分）已知函数f(x)=(x+a)ex+x-a.
(1)若a=1，分析f(x)的单调性；
(2)若a<-2，证明：f(x)在(-∞,0)，(0,+∞)内各恰有一个零点，并且这两个零点互为相反数.
·49·甘肃省九师联盟 2024 届高三下学期 2 月开学考试
数学试题
第I卷(选择题)
一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求
的。
1.已知集合A={x∣0<x+1<2},B={x∣x<0或x>2}，则A∩B= ( )
A.{x∣-1<x<0} B.{x∣2<x<3}
C.{x∣x<1或x>2} D.{x∣x<0或2<x<3}
2.sin165°cos525°= ( )
1 3 1 3
A. B. C.- D.-
4 4 4 4
3.已知单位向量a,b满足a+b
=2a-b
，则a,b夹角的余弦值为 ( )
3 3 4 4
A.- B. C.- D.
5 5 5 5
4.已知复数z满足z-3i 2-i =5；则z = ( )
A.2 2 B.2 5 C.8 D.20
5.若直线l:y=2x+4与抛物线C:y2=2px(p>0)只有1个公共点，则C的焦点F到l的距离为 ( )
A. 5 B.2 5 C.3 5 D.4 5
1
6.已知 x+
2 x
n
的展开式中，前三项的系数依次成等差数列，则展开式中二项式系数最大的项是
( )
35 1 7 35
A. x2 B.7x2 C. x2 D.7x2
8 8
7.函数fx
π
=2 cos -3x
4
的单调递减区间是 ( )
π 2kπ π 2kπ
A. - + , +
4 3 12 3
k∈Z
π 2kπ 5π 2kπ
B. + , +
12 3 12 3
k∈Z
π 2kπ π 2kπ
C. - + , +
12 3 12 3
k∈Z
π 2kπ π 2kπ
D. + , +
12 3 4 3
k∈Z
8.已知 fx 是定义域为R的偶函数，且在-∞,0 上单调递减，a= fln1.04 ,b= f1.04 ,c= fe0.04 ，则
( )
A.a<b<c B.a<c<b C.c<b<a D.c<a<b
二、选择题：本题共3小题，每小题6分，共18分。在每小题给出的选项中, 有多项符合题目要求。全部选对
的得6分，部分选对的得3分，有选错的得0分。
·50·9.已知数列a n 满足a =3,2a =3a -2，则 ( ) 1 n+1 n
A. a -2 n 是等差数列 B. a 2n 6 9 的前n项和为 5 4 n -1 +2n
C. a n 2 是单调递增数列 D.数列 a + n+1 3 n 的最小项为4
10.已知函数fx
x+1
=
3
x
-
3
(x∈R，其中 x 表示不大于x的最大整数)，则 ( )
A. fx 是奇函数 B. fx 是周期函数
C. fx 在0,2 上单调递增 D. fx 的值域为0,1
11.已知正四面体ABCD的棱长为4，点P是棱AC上的动点(不包括端点)，过点P作平面β平行于AD､BC，
与棱AB､BD､CD交于Q,S,T，则 ( )
A.该正四面体可以放在半径为 7的球内
8 3
B.该正四面体的外接球与以A点为球心，2为半径的球面所形成的交线的长度为 π
3
C.四边形PQST为矩形
128 3
D.四棱锥C-PQST体积的最大值为
81
第II卷(非选择题)
三、填空题：本题共3小题，每小题5分，共15分．
12.2023年度，网络评选出河南最值得去的5大景点：洛阳龙门石窟，郑州嵩山少林寺，开封清明上河园，洛
阳老君山，洛阳白云山，小张和小李打算从以上景点中各自随机选择一个去游玩，则他们都去洛阳游玩，
且不去同一景点的概率为 .
x2 y2
13.已知F,F 分别是双曲线C: - =1(a>0,b>0)的左､右焦点，过点F 且垂直x轴的直线与C交于
1 2 a2 b2 2
2 5
A,B两点，且tan∠AF 1 F 2 = 5 ，若圆(x-2)2+y2=4与C的一条渐近线交于M,N两点，则 MN =
.
14.若圆锥SO的母线长为3，则圆锥SO体积的最大值为 .
四、解答题：本题共5小题，共77分。解答应写出文字说明、证明过程或演算步骤。
15（. 13分）已知在△ABC中，角A,B,C所对的边分别为a,b,c,ccosB-cosC =c-b cosC.
(1)若A≠2C，证明：△ABC是等腰三角形；
(2)若b=2c=4，求a的值.
16（. 15分）2022年日本17岁男性的平均身高为170.8cm，同样的数据1994年是170.9cm，近30年日本的平
均身高不仅没有增长，反而降低了0.1cm.反观中国近30年，男性平均身高增长了约9cm.某课题组从中
国随机抽取了400名成年男性，记录他们的身高，将数据分成八组：155,160 ,160,165 ,⋯，190,195 ；
同时从日本随机抽取了200名成年男性，记录他们的身高，将数据分成五组：160,165 ,165,170 ,⋯,
180,185 ，整理得到如下频率分布直方图：
·51·(1)由频率分布直方图估计样本中日本成年男性身高的75%分位数；
(2)为了了解身高与蛋白质摄入量之间是否有关联，课题组调查样本中的600人得到如下列联表：
蛋白质摄入量
身高 合计
丰富 不丰富
低于
108
175cm
不低于
100
175cm
合计 600
结合频率分布直方图补充上面的列联表，并依据小概率值α=0.001的独立性检验，推断成年男性身高与
蛋白质摄入量之间是否有关联？
n(ad-bc)2
附：χ2=
a+b c+d a+c b+d
,n=a+b+c+d.
α 0.1 0.05 0.01 0.005 0.001
2.70
x 3.841 6.635 7.879 10.828
α
6
17（. 15分）如图，正方体ABCD-A B C D 的棱长为2,E,F分别为棱AB,CC 的中点.
1 1 1 1 1
(1)请在正方体的表面完整作出过点E,F,D 的截面，并写出作图过程；(不用证明)
1
(2)求点B 到平面EFD 的距离.
1 1
x2 y2
18（. 17分）已知椭圆C: + =1(a>b>0)的离心率为e，点A1,e
a2 b2
在C上，C的长轴长为4e.
(1)求C的方程；
·52·(2)已知原点为O，点P在C上，OP的中点为Q，过点Q的直线与C交于点M,N，且线段MN恰好被点Q
平分，判断OM2⋅ON2-(OM ⋅ON)2是否为定值？若为定值，求出该定值；若不为定值，说明理由.
19（. 17分）已知函数fx
ax+1
=
+lnxa∈R
ex
.
(1)若fx 在0,+∞ 上单调递增，求a的取值范围；
(2)若fx 有2个极值点x 1 ,x 2x 1 >x 2 >0 ，求证：ax2+x2 1 2 >2 e.
·53·广东省衡水金卷 2024 届高三年级 2 月份大联考
数学试题
第I卷(选择题)
一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求
的。
1.已知集合A=x∈Z∣x2≤5
1
,B=-3,-2,-1,0, ,1 2 , 则A∪B中元素的个数为 ( )
A.4 B.5 C.6 D.7
5
2.已知在△ABC中, AB=2,AC=1,cosA= , 则BC= ( )
6
5 5 15
A.1 B. C. D.
2 3 3
3.若a-2b 20=x a20+x a19b+x a18b2+⋯+x ab19+x b20, 则x = ( ) 0 1 2 19 20 19
A.-20 B.-20×219 C.-219 D.20×219
3 3π π
4.若sinα=- ,α∈- ,-
2 2 2
, 则α= ( )
2π 3π 5π 4π
A.- B.- C.- D.-
3 4 4 3
5.若定义在R上的函数fx 满足fx2 =-f-x2 , 则下列结论一定正确的为 ( )
A. fx 的图象关于原点对称 B. fx 的图象关于y轴对称
C. fx 的图象关于点1,0 对称 D. fx 的图象关于直线x=1对称
x2 y2
6.已知点P是曲线Γ: - =1在第一象限内的一点, A为Γ的左顶点, R为PA的中点, F为Γ的右焦
4 4
点. 若直线OR(O为原点)的斜率为 5, 则△PAF的面积为 ( )
A. 10+ 5 B. 10- 5 C.3 2+3 D.3 2-3
7.在某电路上有C、D两个独立工作的元件, 每次通电后, 需要更换C元件的概率为0.2,需要更换D元件
的概率为0.1 , 则在某次通电后C、D有且只有一个需要更换的条件下, C需要更换的概率是 ( )
3 1 9 3
A. B. C. D.
10 50 13 4
8.在各棱长都为2的正四棱锥V-ABCD中, 侧棱VA在平面VBC上的射影长度为 ( )
2 6 2 3
A. B. C. 3 D.2
3 3
二、选择题：本题共3小题，每小题6分，共18分。在每小题给出的选项中, 有多项符合题目要求。全部选对
的得6分，部分选对的得3分，有选错的得0分。
9.若z满足z+z=6,z=z-2i, 则 ( )
·54·A. z的实部为3 B. z的虚部为1
z 1-3i
C. = D. z对应的向量与实轴正方向夹角的正切值为3
3-i 2
10.已知a=2,1 ,b=1,-1 ,c=x,2 , 则 ( )
A.若x=0, 则存在唯一的实数p,q, 使得a=pb+qc
B.若x=1, 则a⊥c
C.若x=4, 则a⎳c
1 1
D.若x=1, 则c在b上的投影向量为- ,
2 2
11.若过点a,b 可作曲线fx =x2lnx的n条切线n∈N , 则 ( )
A.若a≤0, 则n≤2 B.若0<a<e
-3
2, 且b=a2lna, 则n=2
C.若n=3, 则a2lna<b<2ae
-3
2+
1
e-3 D.过e
-3
2,-6
2
, 仅可作y=fx 的一条切线
第II卷(非选择题)
三、填空题：本题共3小题，每小题5分，共15分．
12.如图是一个正四棱台ABCD-A B C D , 已知正四棱台的上、下底面的边长分别为2和6,体积为
1 1 1 1
104 2
, 则侧面积为 ．
3
13.在数列a n 中, a 1 =3, 且a n+1 =3a n +4n-6n∈N* , 则a n 的通项公式为 ．
x2 ∠ACB
14.若圆C与抛物线Γ:y= 在公共点B处有相同的切线, 且C与y轴切于Γ的焦点A,则sin =
6 2
．
四、解答题：本题共5小题，共77分。解答应写出文字说明、证明过程或演算步骤。
15（. 13分）某小区在2024年的元旦举办了联欢会, 现场来了1000位居民. 联欢会临近结束时,物业公司从
现场随机抽取了20位幸运居民进人摸奖环节,这20位幸运居民的年龄用随机变量 X表示,且X∼
N45,225 .
(1)请你估计现场年龄不低于60岁的人数(四舍五人取整数);
(2)奖品分为一等奖和二等奖,已知每个人摸到一等奖的概率为40%, 摸到二等奖的概率为60%, 每个人
摸奖相互独立, 设恰好有n0≤n≤20 个人摸到一等奖的概率为Pn , 求当Pn 取得最大值时n的值.
附:若X∼Nμ,σ2 , 则PX-μ<σ =0.6827,PX-μ<2σ =0.9545.
·55·16（. 15分）如图,在圆雉SO中, 若轴截面SAB是正三角形, C为底面圆周上一点, F为线段OA上一点, D
(不与S重合)为母线上一点, 过D作DE垂直底面于E, 连接OE,EF,DF,CF, CD, 且∠COF=∠EFO.
(1)求证:平面SCO⎳平面DEF;
(2) 若 △EFO 为正三角形, 且 F 为 AO 的中点, 求平面 CDF 与平面 DEF 夹角的余弦值.
17（. 15分）设函数fx =lnx+ax-1 x-2 , 其中a为实数.
(1)当a=1时,求fx 的单调区间;
(2)当fx 在定义域内有两个不同的极值点x 1 ,x 2 时, 证明:fx 1 +fx 2
5 9
> +ln . 9 16
18（. 17分）在直角坐标系xOy中, 已知C 1-1,0 ,C 1,0 2 ,Px,y
,4C P⋅C P=3x2. 1 2
(1)求点P的轨迹C的方程;
(2)设直线l不过坐标原点且不垂直于坐标轴, l与C交于A、B两点, 点Mx 0 ,y 0 x 0 ,y 0 ≠0 为弦AB的中
点. 过点M作l的垂线交C于D、E,N为弦DE的中点.
①证明:l与ON相交;
②已知l与直线ON交于T, 若ON=λNTλ>0 , 求λ的最大值.
19（. 17分）在无穷数列a n 中, 令T n =a 1 a 2 ⋯a n , 若∀n∈N*,T n ∈a n , 则称a n 对前n项之积是封闭的.
(1)试判断:任意一个无穷等差数列a n 对前n项之积是否是封闭的?
(2)设a n 是无穷等比数列, 其首项a 1 =2, 公比为q. 若a n 对前n项之积是封闭的,求出q的两个值(若
多求, 则按前2个计分);
(3)证明:对任意的无穷等比数列a n , 总存在两个无穷数列b n 和c n , 使得a n =b n ⋅c nn∈N* , 其中
b n 和c n 对前n项之积都是封闭的.
·56·前，积分同者名次并列)，积分规则为每队胜一场得3分，平场得1分，负一场得0分．若每场比赛中两队
1
胜、平、负的概率均为 ，则在比赛结束时丙队在输了第一场且其积分仍超过其余三支球队的积分的概
3
率为 ( )
1 5 4 8
A. B. C. D.
9 27 81 243
8.已知函数fx 及其导函数f x 定义域均为R，记gx =f x+1 ，且f(2+x)-f(2-x)=4x，g3+x
为偶函数，则g 7 +g17 = ( )
A.0 B.1 C.2 D.3
二、选择题：本题共3小题，每小题6分，共18分。在每小题给出的选项中, 有多项符合题目要求。全部选对
的得6分，部分选对的得3分，有选错的得0分。
9.下列说法正确的是 ( )
A.用简单随机抽样从含有50个个体的总体中抽取一个容量为10的样本，个体m被抽到的概率是0.2
B.已知一组数据1，2，m，6，7的平均数为4，则这组数据的方差是5
C.数据27，12，14，30，15，17，19，23的50%分位数是17
D.若样本数据x ，x ，⋯，x 的标准差为8，则数据2x -1，2x -1，⋯，2x -1的标准差为16
1 2 10 1 2 10
10.已知函数 fx =ex-1+e1-x+x2-2x，若不等式 f(2-a)< fx2+3 对任意的x∈R恒成立，则实数a的取
值可能是 ( )
1
A.-4 B.- C.1 D.2
2
11.已知正方体ABCD-A B C D 的棱长为1，M是棱A B 的中点．P是平面CDD C 上的动点(如图)，则
1 1 1 1 1 1 1 1
下列说法正确的是 ( )
·58·A.若点P在线段C D上，则BP⎳平面B D A
1 1 1
B.平面PBD ⊥平面A C D
1 1 1
C.若∠MBP=∠MBD ，则动点P的轨迹为抛物线
1
D.以△ABA 的一边A B所在直线为旋转轴，其余两边旋转一周，在旋转过程中，三棱锥A-BDC 体积
1 1 1
的取值范围为
1
-
2
,
1
+
2
6 12 6 12
第II卷(非选择题)
三、填空题：本题共3小题，每小题5分，共15分．
x
12.2-
y
(x+y)6的展开式中x2y4的系数为 ．
x2 y2
13.已知正数x，y满足x+y=6，若不等式a≤ + 恒成立，则实数a的取值范围是 ．
x+1 y+2
14.斐波那契数列 ( Fibonaccisequence) ，又称黄金分割数列 ，因数学家莱昂纳多·斐波那契
(LeonardoFibonacci)以兔子繁殖为例子而引入，故又称为“兔子数列”，指的是这样一个数列：1、1、2、
3、5、8、13、21、34、⋯，在数学上，斐波那契数列以如下递推的方式定义：a =1,a =1,a =a +a (n≥
0 1 n n-1 n-2
2,n∈N*),A=a ,a ,⋯,a
1 2 2024
,B⊆A且B≠∅中，则B中所有元素之和为奇数的概率为 ．
四、解答题：本题共5小题，共77分。解答应写出文字说明、证明过程或演算步骤。
15.(13分)在△ABC中，已知内角A、B、C的对边分别为a、b、c，且△ABC的面积为 3，点D是线段BC上
靠近点B的一个三等分点，AD=1．
π
(1)若∠ADC= ，求c；
3
(2)若b2+4c2=11，求sin∠BAC的值．
16.(15分)如图，在三棱锥D-ABC中，AB=AD=BD=3 2,AC=7,BC=CD=5．
(1)证明：平面ACD⊥平面ABC；
·59·
(2)若E是线段CD上的点，且CD=4CE，求二面角E-AB-C的正切值．
x2 y2
17.(15分)已知椭圆E: 9 + 5 =1的左右顶点分别为A、B，点C在E上，点M6,y M ,N6,y N 分别为直线
AC、BC上的点.
(1)求y ⋅y 的值；
M N
(2)设直线BM与椭圆E的另一个交点为D，求证：直线CD经过定点.
18.(17分)设X,Y 是一个二维离散型随机变量，它们的一切可能取的值为a,b i j ，其中i,j∈N*，令p = ij
PX=a,Y=b i j ，称p i,j∈N* ij 是二维离散型随机变量X,Y 的联合分布列，与一维的情形相似，我们
也习惯于把二维离散型随机变量的联合分布列写成下表形式；
X,Y b b b ⋅⋅⋅
1 2 3
a p p p ⋅⋅⋅
1 11 12 13
a p p p ⋅⋅⋅
2 21 22 23
a p p p ⋅⋅⋅
3 31 32 33
⋅⋅⋅ ⋅⋅⋅ ⋅⋅⋅ ⋅⋅⋅ ⋅⋅⋅
现有nn∈N* 个球等可能的放入编号为1,2,3的三个盒子中，记落入第1号盒子中的球的个数为X，落
入第2号盒子中的球的个数为Y．
(1)当n=2时，求X,Y 的联合分布列，并写成分布表的形式；
n
(2)设p k = PX=k,Y=m
m=0
n
,k∈N且k≤n，求kp 的值． k
k=0
(参考公式：若X~Bn,p
n
，则kC n kpk 1-p
k=0
n-k=np)
19.(17分)已知函数fx =xlnx-a2x2+1 (a∈R).
(1)若a=-1，求fx 的图象在x=1处的切线方程；
(2)若fx 有两个极值点x ，x (x <x ). 1 2 1 2
①求a的取值范围；
1
②求证：3x -x > -2.
2 1 a
·60·江西省上进联盟 2023-2024 学年高三下学期一轮总复习（开学
考）验收考试数学试卷
第I卷(选择题)
一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求
的。
1.已知集合M=x|x(x-3)<4 ,N=y|y<3 ，则M∩N= ( )
A.∅ B. x|-4<x<3 C. x|-1<x<3 D. x|1<x<3
2.已知定义在R上的函数fx =x5+a+1 x4-2024的导函数f x 为偶函数.则fa = ( )
A.-2025 B.-2024 C.-1 D.2025
3.已知F是抛物线C:x=2y2的焦点，点M2,m 在抛物线C上，则MF = ( )
3 5 9 17
A. B. C. D.
2 2 8 8
4.研究表明，地震时释放的能量E(单位：焦耳)与地震里氏震级M之间的关系为lgE=4.8+1.5M.2023年
12月18日在甘肃积石山县发生了里氏6.2级地震，2024年1月4日在斐济群岛发生了里氏5.7级地震，
若前后这两个地震释放的能量之比是n，则n的整数部分为 ( )
A.3 B.4 C.5 D.6
5.已知一正方体木块ABCD-A B C D 的棱长为4，点E在校AA 上，且AE=3.现过D,E,B 三点作一截面
1 1 1 1 1 1
将该木块分开，则该截面的面积为 ( )
5 17
A.4 26 B.5 17 C.2 26 D.
2
6.已知复数z=a+bia,b∈R .且2-i-z
b+a
=1，则 的取值范围为 ( )
a+1
-3- 3 -3+ 3 A. ,
4 4
-3- 3 B. -∞,
4
-3+ 3 ∪ ,+∞
4
1- 3 1+ 3 C. ,
4 4
1- 3 D. -∞,
4
1+ 3 ∪ ,+∞
4
7.已知函数 fx =sinωx+φ
1 π π
+ ω>0,- <φ<
2 2 2
，其导函数为 f x .且 f0 ⋅ f 0 =0，fx 在
区间0,2π 上恰有4个不同的实数x ii=1,2,3,4 ，使得对任意x都满足fx +f2x 1 -x)=1，且对任意
·61·角α,fx
π
在区间α,α+
2
上均不是单调函数.则ω的取值范围是 ( )
19 25
A. ,
12 12
25
B. 2,
12
19
C. ,2
12
25
D. ,+∞
12
8.142857被称为世界上最神秘的数字，142857×1=142857,142857×2=285714,142857×3=428571,
142857×4=571428,142857×5=714285,142857×6=857142，所得结果是这些数字反复出现，若a=
ln1.285714
e0.142857,b= +1,c= 1.285714，则 ( )
2
A.a>b>c B.c>b>a C.b>a>c D.a>c>b
二、选择题：本题共3小题，每小题6分，共18分。在每小题给出的选项中, 有多项符合题目要求。全部选对
的得6分，部分选对的得3分，有选错的得0分。
9.已知平面向量a,b在由正方形组成的网格中位置如图所示(网格中面积最小的正方形边长为1)，则
( )
A. b
= 2 B.存在实数λ，使得b=λa.
C. a+2b
1
⋅b=7. D.向量b在a方向上的投影向量为- a
3
10.化学中经常碰到正八面体结构(正八面体是每个面都是正三角形的八面体)，如六氟化硫(化学式SF)､
6
金刚石等的分子结构.将正方体六个面的中心连线可得到一个正八面体(如图1)，已知正八面体E-
ABCD-F的(如图2)棱长为2，则 ( )
8π
A.正八面体E-ABCD-F的内切球表而积为
3
8π
B.正八面体E-ABCD-F的外接球体积为
3
C.若点P为棱EB上的动点，则AP+CP的最小值为2 3
2 2
D.若点Q为棱AF上的动点，则四棱锥E-QBC的体积为定值
3
11.已知数列a n
1
的前n项和为S ,a =1，且9a a =a -4a ，数列 n 1 n n+1 n n+1 a
n
与数列4na n a n+1 的前n项和分别
·62·为R ,T，则 ( )
n n
a 1 1 43
A. n+1 > B.T< C.S < D. R ≥6n2-5n
a 4 n 3 n 39 n
n
第II卷(非选择题)
三、填空题：本题共3小题，每小题5分，共15分．
12.已知等差数列a n
3π
的前n项和为S ,a +a = ，则cosS = . n 3 10 8 12
13.“圆排列”亦称“循环排列”“环排列”，最早出现在中国《易经》的四象八卦组合.当A，B，C三位同学围成
一个圆时，其中一个排列“ABC”与该排列旋转一个或几个位置得到的排列“BCA”或“CAB”是同一个排
列，现有六位同学围成一个圆做游戏，其排列总数为 .(用数字作答)
x2 y2
14.已知双曲线C: - =1(a>0,b>0)的左､右焦点分别为F,F，过点F 且斜率为1的直线l与C的右
a2 b2 1 2 2
支交于A,B两点，若△FAB的内心恰好在它的一条高线上，则C的离心率为 .
1
四、解答题：本题共5小题，共77分。解答应写出文字说明、证明过程或演算步骤。
3cosA acosC ccosA
15.(13分)在△ABC中，内角A,B,C所对的边分别为a,b,c，且 - = .
3 2b 2b
(1)求A；
(2)若a2+c2-b2=ac，点D在边AB上，BD=2AD,CD= 13.求△ABC的面积.
16.(15分)2024年1月5日起，第40届中国·哈尔滨国际冰雪节在黑龙江省哈尔滨市举行.让大家对冰雪文
化进一步了解，激发了大家对冰雪运动进一步的热爱.为了调查不同年龄层的人对“冰雪运动”的喜爱态
度.某研究小组随机调查了哈尔滨市M社区年龄在[20,70)的市民300人，所得结果统计如下频数分布
表所示
年龄a(单位：周岁) 20,30 30,40 40,50 50,60 60,70
频数 30 81 99 60 30
持喜爱态度 24 65 75 30 12
(1)求该样本中市民年龄的平均数；(同一组中的数据用该区间的中点值作代表)
(2)从这300名市民中随机抽取1人，在此人喜爱冰雪运动的前提下，求其年龄小于50周岁的概率：
(3)为鼓励市民积极参加这次调查，该研究小组决定给予参加调查的市民一定的奖励，奖励方案有两种：
方案一：按年龄a进行分类奖励，当a<30时，奖励10元：当30≤a<50时，奖励30元：当a≥50时，奖
励40元；
方案二：利用抽奖的方式获得奖金，其中年龄低于样本中位数的可抽1次奖，年龄不低于样本中位数的可
抽2次奖.每次抽中奖励30元，未抽中奖励10元，各次抽奖间相互独立，且每次抽奖中奖的概率均为了
2
3
将频率视为概率，利用样本估计总体的思想，若该研究小组希望最终发出更多的奖金，则从期望角度出
发.该研究小组应采取哪种方案
·63·17.(15分)已知等边△ABC的边长为4，E,F,H分别是边AB,BC,AC的中点(如图1)，现以EF为折痕把
△BEF折起，使点B到达点B的位置，且HB=3(如图2).
(1)证明：AC⊥HB；
3 BM
(2)在线段BH上是否存在点M，使得M到平面BEF的距离为 ，若存在，求出 的值；若不存在，请
4 MH
说明理由.
x2 y2
18.(17分)已知椭圆C: + =1的右焦点为F，过N2,0
6 3
的直线L与C交于A,B两点.
(1)若点M为C上一动点，求MF +MN 的最大值与最小值；
(2)若AN=2NB，求l的斜率；
(3)在x轴上是否存在定点Q，使得QA⋅QB为定值？若存在，求出定点Q的坐标；若不存在，请说明理由.
19.(17分)已知函数gx
a
=1-2lnx- (a>0)，且gx x2 的极值点为x . 0
(1)求x ；
0
(2)证明：2gx 0
2
+2≤ ； a
(3)若函数gx
1 1
有两个不同的零点x 1 ,x 2 ，证明： x2 + x2 >2gx 0
1 2
+2.
·64·重庆市缙云教育联盟 2024 届高三下学期 2 月月度质量检测
数学试题
第I卷(选择题)
一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求
的。
1.①植物根据植株的高度及分枝部位等可以分为乔木、灌木和草木三大类，某植物园需要对其园中的不同
植物的干重(烘干后测定的质量)进行测量；②检测员拟对一批新生产的1000箱牛奶抽取10箱进行质量
检测；上述两项调查应采用的抽样方法是 ( )
A.①用简单随机抽样，②用分层随机抽样 B.①用简单随机抽样，②用简单随机抽样
C.①用分层随机抽样，②用简单随机抽样 D.①用分层随机抽样，②用分层随机抽样
2.下列函数既是奇函数，又在0,+∞ 上单调递增的函数是 ( )
1
A. y=x+ B. y=2x+2-x C. y=lnx D. y=x3
x
3.已知a n 是公比为2的等比数列，若a +a =25，则a = ( ) 1 3 5
A.100 B.80 C.50 D.40
5π
4.若sin +α
12
5 π
= ，则cos2α-
13 6
= ( )
119 50 119 50
A.- B.- C. D.
169 169 169 169
5.已知圆C:x2+2x+y2-1=0，直线mx+ny-1 =0与圆C交于A，B两点.若△ABC为直角三角形，则
( )
A.mn=0 B.m-n=0 C.m+n=0 D.m2-3n2=0
6.已知数列a n
i 5 13
满足a =i，a =i+ ，若a = + i，则正整数k的值是 ( ) 1 n+1 a k 8 10
n
A.8 B.12 C.16 D.20
x2 y2
7.已知椭圆 + =1(a>b>0)的左焦点F，O为坐标原点，点P在椭圆上且不在x轴上，点Q在直线
a2 b2 1
a2 FP
x= 上，若PQ=2FO，F Q=λ 1
c 1 1 FP
1
FO
+ 1
FO
1
(λ>0)，则椭圆的离心率为 ( )
1 3 3-1 5-1
A. B. C. D.
2 2 2 2
8.对于一个古典概型的样本空间Ω和事件A，B，C，D，其中n(Ω)=60，n(A)=30，n(B)=10，n(C)=20，
n(D)=30，n(A∪B)=40，n(A∩C)=10，n(A∪D)=60，则 ( )
A. A与B不互斥 B. A与D互斥但不对立
·65·C.C与D互斥 D. A与C相互独立
二、选择题：本题共3小题，每小题6分，共18分。在每小题给出的选项中, 有多项符合题目要求。全部选对
的得6分，部分选对的得3分，有选错的得0分。
9.已知fx
π
=sinωx+
4
(ω>0)，若p:ω≤2，且p是q的必要条件，则q可能为 ( )
A. fx
π
的最小正周期为π B. x= 是fx
4
图象的一条对称轴
C. fx
π
在 0,
4
上单调递增 D. fx
π π
在 ,
4 2
上没有零点
10.设奇函数fx 与偶函数gx 的定义域均为R，且在区间I上都是单调增函数，则 ( )
A. fx +gx 不具有奇偶性，且在区间I上是单调增函数
B. fx -gx 不具有奇偶性，且在区间I上的单调性不能确定
C. fx gx 是奇函数，且在区间I上是单调增函数
D. f gx 是偶函数，且在区间I上的单调性不能确定
11.对于任意两个正数u，vu<v
1
，记曲线y= 与直线x=u，x=v，x轴围成的曲边梯形的面积为Lu,v
x
，
并约定Lu,u =0和Lu,v =-Lv,u ，德国数学家莱布尼茨(Leibniz)最早发现L1,x =lnx.关于
Lu,v ，下列说法正确的是 ( )
1 1
A. L ,
6 3
=L4,8 B. L450,3100 =100L2,3
C.2Lu,v
v u
< - D. Luu,vu
u v
>v-u
第II卷(非选择题)
三、填空题：本题共3小题，每小题5分，共15分．
12.若命题∃x∈R，-x²-2mx+2m-3≥0为真命题，则m的取值范围为 .
13.在多面体PABCQ中，PA=PB=PC=AB=AC=BC=2，QA=QB=QC且QA，QB，QC两两垂直，则
该多面体的外接球半径为 ，内切球半径为 ．
1 1 14.已知x ,x 为方程x2- -
1 2 tanβ tanα+β
2 π x+ =0的两个实数根，且α,β∈0,
3 2
，x =3x ，则tanα的
1 2
最大值为 .
四、解答题：本题共5小题，共77分。解答应写出文字说明、证明过程或演算步骤。
15（. 13分）已知在一个不透明的盒中装有一个白球和两个红球(小球除颜色不同，其余完全相同)，某抽球试
验的规则如下：试验者在每一轮需有放回地抽取两次，每次抽取一个小球，从第一轮开始，若试验者在某
轮中的两次均抽到白球，则该试验成功，并停止试验.否则再将一个黄球(与盒中小球除颜色不同，其余
完全相同)放入盒中，然后继续进行下一轮试验.
(1)若规定试验者甲至多可进行三轮试验(若第三轮不成功，也停止试验)，记甲进行的试验轮数为随机变
量X，求X的分布列和数学期望；
·66·(2)若规定试验者乙至多可进行nn∈N* 轮试验(若第n轮不成功，也停止试验)，记乙在第
kk∈N*,k≤n
n
轮使得试验成功的概率为P k ，则乙能试验成功的概率为P(n)=P k ，证明：Pn
k=1
1
< . 3
16（. 15分）如图，AB是半球O的直径，AB=4,M,N是底面半圆弧AB上的两个三等分点，P是半球面上一
点，且∠PON=60°．
(1)证明：PB⊥平面PAM：
(2)若点P在底面圆内的射影恰在ON上，求直线PM与平面PAB所成角的正弦值．
17（. 15分）设a∈R，函数fx
π
=sin2x-cosx-a，x∈ ,π
2
.
(1)讨论函数fx 的零点个数；
(2)若函数fx
1
有两个零点x ，x ，试证明： ≤tanx tanx -3. 1 2 1-tanx tanx 1 2
1 2
18（. 17分）已知抛物线：y2=2x，直线l:y=x-4，且点B,D在抛物线上．
(1)若点A,C在直线l上，且A,B,C,D四点构成菱形ABCD，求直线BD的方程；
(2)若点A为抛物线和直线l的交点(位于x轴下方)，点C在直线l上，且A,B,C,D四点构成矩形ABCD，
求直线BD的斜率．
19（. 17分）固定项链的两端，在重力的作用下项链所形成的曲线是悬链线.1691年，莱布尼茨等得出“悬链
cec x +e - c x
线”方程y=
ex+e-x
，其中c为参数.当c=1时，就是双曲余弦函数coshx= ，类似地我们可以
2 2
ex-e-x
定义双曲正弦函数sinhx= .它们与正、余弦函数有许多类似的性质.
2
(1)类比正弦函数的二倍角公式，请写出双曲正弦函数的一个正确的结论:sinh2x= .(只写出即可，
不要求证明)；
(2)∀x∈[-1,1]，不等式cosh2x+mcoshx≥0恒成立，求实数m的取值范围；
π 3π
(3)若x∈ ,
4 2
，试比较cosh(sinx)与sinh(cosx)的大小关系，并证明你的结论.
·67·湖南省名校教育联盟 2024 届高三下学期入学摸底考试
数学试题
第I卷(选择题)
一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求
的。
1
1.设复数z满足 =-i，则z
1-z
= ( )
1 2
A. B. C.1 D. 2
2 2
2.已知集合A= x log x≥1 1
2
，B= y 1 y= 2 x ,x≥2 ，则A∩B= ( )
1
A. 0,
4
1
B. 0,
2
1 1
C. ,
4 2
1
D. ,+∞
2
3.下图为某商家2023年1月至10月某商品的月销售量，则下列说法正确的是 ( )
A.这10个月的月销售量的中位数为28
B.这10个月的月销售量的平均数为31
C.这10个月的月销售量的第75百分位数为34.5
D.前5个月的月销售量的方差大于后5个月的月销售量的方差
4.设正四面体ABCD的棱长为1，E为CD的中点，F，G分别是棱AC,BC上的点，且满足AF=2CG=λ，
GF⎳平面ABE，则λ的值是 ( )
1 1 2 3
A. B. C. D.
3 2 3 4
5.已知正项等比数列a n (其公比q∈0,1 )的前n项积为T，设甲：a a =a ，乙：T 有最大值T，则甲是乙 n 1 11 7 n 5
的 ( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
π
6.若cos -α
6
1 π
= ，则sin2α+
3 6
= ( )
4 2 4 2 7 7
A. B.- C. D.-
9 9 9 9
·68·7.已知抛物线C：x2=4y的焦点为F，过点F的直线与C交于A,B两点，若D为C的准线上一点，且|AF|=
|AD|=3，则△ABD的面积为 ( )
15 15 9 2
A. B. C. D.9 2
4 2 2
f(x )-f(x )
8.已知函数f(x)=xlnx-x，若∀x >0,x >0，且x ≠x ，恒有 1 2 <1，则正实数t的取值范围为
1 2 1 2 etx1-etx2
( )
1
A.[e,+∞) B. ,+∞
e
C. 0,e
1
D. 0,
e
二、选择题：本题共3小题，每小题6分，共18分。在每小题给出的选项中, 有多项符合题目要求。全部选对
的得6分，部分选对的得3分，有选错的得0分。
9.一个正方体的顶点都在球面上，过球心作一截面，如图所示，则截面的可能图形是 ( )
A. B. C. D.
10.如图，圆C与x轴相切于点T(1，0)，与y轴正半轴交于A，B两点，且AB
3
= ，过点A任作一条直线与
2
圆O:x2+y2=1相交于M，N两点，则 ( )
A.圆C的方程为x-1 5 2+y-
4
2 25 =
16
B.圆C与圆O的相交弦所在直线方程为4x+5y+4=0
|MA| |NB| 5
C. + =
|MB| |NA| 2
|MA| |NB| 3
D. - =
|MB| |NA| 2
π π
11.已知函数f(x)=cos(ωx-φ)(ω>0)在 - ,
3 6
π
上单调，且f
6
4π
=f
3
π
=-f-
3
，则ω的取值可
能为 ( )
3 7 9 12
A. B. C. D.
5 5 5 7
第II卷(非选择题)
三、填空题：本题共3小题，每小题5分，共15分．
·69·12.甲、乙、丙、丁共四名同学进行劳动技能比赛，决出第1名到第4名的名次，已知甲不是第1名，乙不是第
4名，则这4个人名次排列的可能情况共有 种．
13.若数列a n
a
满足a =8，a = a +n，则 n 的最小值是 ． 1 n+1 n n
x2 y2
14.已知△ABC的三个顶点都在椭圆Γ: + =1(a>b>0)上，其中A，B分别为Γ的左顶点和上顶点，
a2 b2
若以B为顶角的等腰△ABC恰好有3个，则直线AB的斜率的取值范围为 ．
四、解答题：本题共5小题，共77分。解答应写出文字说明、证明过程或演算步骤。
C
15（. 13分）在△ABC中，已知3tan =2sin(A+B)．
2
(1)求角C的大小；
(2)若AB=3AD，CD=2AD，试判断△ABC的形状并说明理由．
16（. 15分）如图，三棱柱ABC-A B C 中，侧面AA B B是边长为2的正方形，D，E分别为AB，BB 的中点，
1 1 1 1 1 1
若AE⊥A C，平面ABC⊥平面AA B B．
1 1 1
(1)求证：CD⊥平面AA B B；
1 1
(2)若三棱柱ABC-A B C 的体积为4，求直线AE与平面A BC所成角的正弦值．
1 1 1 1
17（. 15分）某电视台综艺节目邀请甲、乙两位好友参加了“心有灵犀、竟猜谜语”活动：即从5个谜语中随机
抽取3个，让甲负责比划，乙负责猜谜语．已知甲会比划其中3个谜语，这3个谜语乙猜对的概率都为
2
，另外2个不会比划的谜语乙无法猜对．
3
(1)求甲、乙配合猜对1个谜语的概率；
(2)设甲、乙配合猜对谜语个数为X，求X的分布列和数学期望．
18（. 17分）设动点Mx,y 与定点F 2 2,0
2
的距离和它到定直线l:x= 的距离之比等于 2，记点M的轨
2
迹为曲线C．
(1)求曲线C的方程；
(2)设F(- 2,0)过点F 的直线与C的右支相交于A，B两点，I是△FAB内一点，且满足|FB|⋅IA+
1 2 1 1
|BA|⋅IF +|AF|⋅IB=0，试判断点I是否在直线l上，并说明理由．
1 1
19（. 17分）已知函数f(x)=x2-1-axlnx,a∈R．
(1)若fx 是单调递增函数，求a的取值范围；
(2)若fx
7
存在三个零点x ,x ,x ，且x +x +x < ，求a的取值范围． 1 2 3 1 2 3 2
·70·π π π π
A. B. C. D.
3 2 4 6
7.过原点O的直线l:y=kx与圆M:x2-6x+y2-6y+16=0交于A,B两点，且OA =AB ，则k= ( )
1
A.1 B.2 C. D. 2
2
8.已知函数 f x =sinωx+φ (ω>0)，若任意φ∈ R,f x
π
在 0,
2
上有零点，则ω的取值范围为
( )
A. 0,+∞ B. 1,+∞ C. 2,+∞ D. 3,+∞
二、选择题：本题共3小题，每小题6分，共18分。在每小题给出的选项中, 有多项符合题目要求。全部选对
的得6分，部分选对的得3分，有选错的得0分。
x2 y2
9.已知双曲线C: - =1(a>0,b>0)的左､右焦点分别为F,F,O为坐标原点，直线y=b与双曲线C
a2 b2 1 2
的渐近线交于点A,B(A在第二象限，B在第一象限)，下列结论正确的是 ( )
A. BF⊥BF
1 2
B. BF∥AO
2
C.若△OAB的面积为2，则双曲线C的焦距的最小值为4
D.若△OAB的面积为2，则双曲线C的焦距的最小值为8
10.
如图，三角形数阵由一个等差数列2,5,8,11,14,⋯排列而成，按照此规律，下列结论正确的是 ( )
A.数阵中前7行所有数的和为1190 B.数阵中第8行从左至右的第4个数是101
C.数阵中第10行的第1个数是137 D.数阵中第10行从左至右的第4个数是146
11.已知定义在R上的函数fx 满足fx × fx -fx-y =fxy ，当x∈-∞,0 ∪0,+∞ ，时，fx
≠0.下列结论正确的是 ( )
1
A. f
2
1
= B. f10
2
=1 C. fx 是奇函数 D. fx 在R上单调递增
第II卷(非选择题)
·72·三、填空题：本题共3小题，每小题5分，共15分．
p
12.已知抛物线C:y2=2px(p>0)的焦点为F，点P ,a
4
在抛物线C上，且PF =3，则p= .
13.甲､乙两位同学进行羽毛球比赛，约定赛制如下：累计赢2局者胜，分出胜负即停止比赛.已知甲每局赢的
3
概率为 ，每局比赛的结果相互独立.本次比赛到第3局才分出胜负的概率为 ，本次比赛甲获胜
5
的概率为 .
14.如图，将正四棱柱ABCD-A B C D 斜立在平面α上，顶点C 在平面α内，AC ⊥平面α,AA =2AB=6.
1 1 1 1 1 1 1
点P在平面α内，且PC = 3.若将该正四棱柱绕AC 旋转，PC的最大值为 .
1 1
四、解答题：本题共5小题，共77分。解答应写出文字说明、证明过程或演算步骤。
15（. 13分）已知正项等比数列a n 满足a +a =6,a a =a . 1 2 1 3 1
(1)求a n 的通项公式；
(2)记a n
M +m
的前n项中最大值为M n ，最小值为m n (规定：M 1 =m 1 =a 1 )，令b n = n 2 n，求数列b n 的前n
项和S .
n
16（. 15分）将3个数字1，2，3随机填入如下99个空格中，每个空格中最多填一个数字，且填入的3个数字
从左到右依次变大.
(1)求数字2填在第2个空格中的概率；
(2)记数字2填在第x个空格中的概率为Px ，求Px 的最大值.
17（. 15分）如图，在四棱锥P-ABCD中，四边形ABCD是菱形，PA⊥AC,BD⊥PC,PA=AB.
(1)证明：PA⊥平面ABCD.
(2)若PC=4PE,∠ABC=60°，求二面角A-BD-E的余弦值.
·73·x2 y2
18（. 17分）已知椭圆C的方程为 + =1(a>b>0)，右焦点为F1,0
a2 b2
1
，且离心率为
2
(1)求椭圆C的方程；
3 (2)过点F的直线l与椭圆C交于A,B两点，证明:圆x-
4
2 +y2= 25 恒与以弦AB为直径的圆相切.
16
19（. 17分）已知函数fx = 2x-a.
(1)若曲线y=fx 在点 a,fa 处的切线过点4,2 ，求a的值；
(2)若fx ≤aex-1恒成立，求a的取值范围.
·74·山东省齐鲁名校联盟 2024 届高三下学期开学质量检测
数学试题
第I卷(选择题)
一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求
的。
1.已知集合A=x x-1<3 ,B=x5≤x≤12 ，则A∩B= ( )
A. 5,10 B. 1,12 C. 5,10 D. 1,12
2.已知复数z=-1+i,z-az=-6+bia,b∈R ，则b= ( )
A.-5 B.-4 C.-3 D.-1
x2 y2
3.“3<m<11”是“方程 + =1表示焦点在y轴上的椭圆”的 ( )
11-m m-3
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
4.已知圆台的母线长为2 37，上、下底面的直径分别为6和10，则该圆台的体积为 ( )
A.184π B.188π C.192π D.196π
1
5.已知a=log 7,b=log 36,c=
3 9 2
-0.5
，则 ( )
A.a>c>b B.a>b>c C.b>a>c D.b>c>a
π
6.已知θ∈ ,π
2
12 sin2θ-cos2θ
,tan2θ= ，则 = ( )
5 cos2θ+4sin2θ
16 1 1 16
A.- B.- C. D.
31 7 7 31
7.已知向量a,b,c满足a
=b
=2，a-b
=2，2a-c
= 3，则c-b 的最大值为 ( )
A. 3 B.2 3 C.3 3 D.4 3
8.已知函数f(x)=mx2-xlnx存在极小值点x ，且f(x )<-e3，则实数m的取值范围为 ( )
0 0
1
A. 0,
e2
2
B. 0,
e2
1
C. 0,
e3
2
D. 0,
e3
二、选择题：本题共3小题，每小题6分，共18分。在每小题给出的选项中, 有多项符合题目要求。全部选对
的得6分，部分选对的得3分，有选错的得0分。
1 9.已知 -2x2
x
n 的展开式中，各项的二项式系数之和为128，则 ( )
A.n=7 B.只有第4项的二项式系数最大
C.各项系数之和为1 D. x5的系数为560
·75·10.已知函数fx =Acosωx+φ
π π
A>0,ω>0,- <φ<
2 2
的部分图象如图所示，则 ( )
π
A.φ=
4
B. fx
kπ 3π
图象的对称中心为 + ,0
2 8
,k∈Z
C. fx
π
在 ,π
2
上的值域为-2 2,2
D.将fx
5π
的图象向左平移 个单位长度后得gx
8
=-2 2sin2x的图象
11.在四棱锥S-ABCD中，ABCD是矩形，AD⊥SD,∠SDC=120°,SD=CD=2BC=2,P为棱SB上一点，
则下列结论正确的是 ( )
A.点C到平面SAD的距离为 3
3
B.若SP=PB，则过点A,D,P的平面α截此四棱锥所得截面的面积为
2
C.四棱锥S-ABCD外接球的表面积为17π
3
D.直线AP与平面SCD所成角的正切值的最大值为
3
第II卷(非选择题)
三、填空题：本题共3小题，每小题5分，共15分．
12.已知等比数列a n 中，a a a =-8,a =64，则a = ． 3 4 5 9 5
13.某工厂由甲、乙两条生产线来生产口罩，产品经过质检后分为合格品和次品，已知甲生产线的次品率为
4%，乙生产线的次品率为7%，且甲生产线的产量是乙生产线产量的2倍．现在从该工厂生产的口罩中
任取一件，则取到合格品的概率为 ．
14.已知抛物线y2=4x的焦点为F，准线为l，过点F的直线交抛物线于A,B两点，点A,B在直线l上的射影
分别为A 1 ,B 1 两点，以线段A 1 B 1 为直径的圆C与y轴交于M,N两点，且MN
4
= AB 5 ，则直线AB的斜率
为 ．
四、解答题：本题共5小题，共77分。解答应写出文字说明、证明过程或演算步骤。
15（. 13分）记数列a n 的前n项和为S ，已知a =3,na =2S +3n． n 1 n+1 n
(1)证明：a +a =2a ；
n+2 n n+1
b 1
(2)若 a n = 3n+1 ，求数列b n
n
的前n项和T． n
·76·16（. 15分）如图，在三棱锥ABC-A B C 中，D,E分別是梭BC,AA 的中点．
1 1 1 1
(1)在棱BB 上找一点F，使得平面DEF⎳平面A B C，并证明你的结论；
1 1 1
(2)若AA = 3,△ABC是边长为2的等边三角形，A D=AD,BC⊥DE，求二面角B -A C-C 的正弦
1 1 1 1 1
值．
17（. 15分）某市为繁荣地方经济，大力实行人才引进政策，为了解政策的效果，统计了2018-2023年人才引
进的数量y(单位：万人)，并根据统计数据绘制了如图所示的散点图(x表示年份代码，年份代码1-6分
别代表2018-2023年)．
(1)根据散点图判断y=blnx+a与y=ec+dx(a,b,c,d均为常数)哪一个适合作为y关于x的回归方程类
型；(给出结论即可，不必说明理由)
(2)根据(1)的结果及表中的数据，求出y关于x的回归方程，并预测该市2025年引进人才的数量；
(3)从这6年中随机抽取4年，记引进人才数量超过4万人的年数为X，求X的分布列和数学期望．
参考数据：
6
y w ∑ x-x
i i=1
6
∑
2 i=1
x-x i
y-y i
6
∑
i=1
x-x i
w-w
i
5.15 1.55 17.5 20.95 3.85
1 6
其中w= w,w=lny,e2.44≈11.47,e2.54≈12.68．
6 i i i
i=1
参考公式：对于一组数据u 1 ,v 1 ,u 2 ,v 2 ,⋯,u n ,v n ，其回归直线v=α+βu的斜率和截距的最小二乘估计
n
∑ u-u
i
分别为：β= i=1
v-v
i
n
∑ u-u
i
i=1
,α=v-βu．
2
·77·x2 y2 5
18（. 17分）已知双曲线C: a2 - b2 =1(a>0,b>0)的离心率为 2 ，左、右顶点分别为A 1 ,A 2 ，点B0,1 ，且
△A BA 的面积为2．
1 2
(1)求C的方程；
(2)若过点B的直线l与C的左、右两支分别交于M,N两点，直线A M,A N交于点P，直线l与x轴交于
1 2
点Q,O为坐标原点，证明：OP⋅OQ为定值．
19（. 17分）已知函数fx =mx2-x+1 e-x．
(1)当m≥0时，求fx 的单调区间；
(2)若函数gx =ex+fx ex-2恰有两个零点，求实数m的取值范围．
·78·浙江省名校协作体 2023-2024 学年高三下学期开学联考
数学试题
第I卷(选择题)
一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求
的。
1.已知全集U=R,A=x∣x≥0 ,B={x∣-1<x<1}，则{x∣-1<x<0}= ( )
A. A∪B B. ∁ U A ∩B C. A∩∁ U B D.∁ UA∩B
2
2.已知复数z满足z= ，则z⋅z= ( )
1-i
A.-2 B.2i C. 2 D.2
cosθ-sinθ π
3.已知 =2，则tanθ-
cosθ+sinθ 4
= ( )
1 1
A.-2 B.2 C.- D.
2 2
4.柳编技艺在我国已有上千年的历史，如今柳编产品已经入选国家非物质文化遗产名录.如图所示；这是
用柳条编织的圆台形米斗，上底直径30cm，下底直径20cm，高为30cm，则该米斗的容积大概为 ( )
A.9升 B.15升 C.19升 D.21升
5.有一组数据：1,1,2,2,3,3,4,4,4,4，去掉该组中的一个数据，得到一组新的数据.与原有数据相比，无论去
掉哪个数据，一定变化的数字特征是 ( )
A.平均数 B.众数 C.中位数 D.极差
6.已知a>1,b>0，若 a+log a=b+log b，则 ( )
2 2
A.a>2b B.a<2b C.a>b2 D.a<b2
7.已知正项数列 a n 满足a 2 =3a 1 ,S n 为a n 的前n项和，则“a n 是等差数列”是“ S 为等差数列”的 n
( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分又不必要条件
8.已知平面向量a,b满足a
=1,b,a+b
π
= ，则a-b
6
的最大值为 ( )
·79·A.2 B. 2+1 C. 3+1 D.3
二、选择题：本题共3小题，每小题6分，共18分。在每小题给出的选项中, 有多项符合题目要求。全部选对
的得6分，部分选对的得3分，有选错的得0分。
π
9.已知x= 为函数fx
6
=sin2x+acos2x的一个极大值点，则 ( )
A.函数fx 的值域为-2,2
π
B.函数y=fx-
12
为奇函数
C.曲线y=fx
5π
关于直线x=- 对称 D.函数y=fx
6
5π π
在- ,
6 6
上单调递增
10.三棱锥P-ABC各顶点均在半径为2的球O的表面上，AB=AC=2,∠BAC=90°，二面角P-BC-A的
大小为45°，则下列结论正确的是 ( )
2 2
A.直线OA∥平面PBC. B.三棱锥O-ABC的体积为
3
C.点O到平面PBC的距离为1 D.点P形成的轨迹长度为2 3π
11.日常生活中植物寿命的统计规律常体现出分布的无记忆性.假设在一定的培养环境下，一种植物的寿命
是取值为正整数的随机变量X，根据统计数据，它近似满足如下规律：对任意正整数n，寿命恰好为n的
植物在所有寿命不小于n的植物中的占比为10%.记“一株植物的寿命为n”为事件A ，“一株植物的寿命
n
不小于n”为事件B .则下列结论正确的是 ( )
n
A. PA 2 =0.01 B. PB n =0.9n-1
C.设a n =PA n+1 ∣B 2 ，则a n 为等比数列 D.设S n =nPA n
n
，则S <10 k
k=1
第II卷(非选择题)
三、填空题：本题共3小题，每小题5分，共15分．
1 x
12.已知正实数x,y满足x+2y=1，则 + 的最小值为 .
x y
x2 y2
13.已知F,F 分别是双曲线C: - =1(a>0,b>0)的左､右焦点，P是圆x2+y2=c2与C的渐近线的一
1 2 a2 b2
个交点，若2∠PFF=∠PFF，则双曲线C的离心率为 .
1 2 2 1
14.已知函数fx
xlnx,x>0,
= 1 若函数gx
-x,x<0,
x
=f fx -afx +1有唯一零点，则实数a的取值范围是
.
四、解答题：本题共5小题，共77分。解答应写出文字说明、证明过程或演算步骤。
15（. 13分）已知△ABC的内角A,B,C的对边分别是a,b,c，且a=2bcosC.
(1)判断△ABC的形状；
(2)若△ABC的外接圆半径为1，求△ABC周长的最大值.
16（. 15分）如图，在等腰直角三角形RBC中，A,D分别为RB,RC的中点，BC=BR=4，将△RAD沿AD折
起，使得点R至点P的位置，得到四棱锥P-ABCD.
·80·(1)若M为PC的中点，求证：DM∥平面PAB；
2
(2)若平面PAD⊥平面ABCD，点E在线段BC上，平面PDE与平面ABED夹角的余弦值为 ，求线段
3
BE的长.
17（. 15分）甲､乙､丙三位同学进行乒乓球比赛，约定赛制如下：每场比赛胜者积2分，负者积0分；比赛前
根据相关规则决定首先比赛的两人，另一人轮空；每场比赛的胜者与轮空者进行下一场比赛，负者下一
场轮空；积分首先累计到4分者获得比赛胜利，比赛结束.已知甲与乙比赛时，甲获胜的概率为p ，甲与丙
1
比赛时，甲获胜的概率为p ，乙与丙比赛时，乙获胜的概率为p .
2 3
(1)若p =p =p =0.5，求比赛结束时，三人总积分X的分布列与期望；
1 2 3
(2)若p +p >1，假设乙获得了指定首次比赛选手的权利，为获得比赛的胜利，试分析乙的最优指定策略.
1 3
18（. 17分）已知过点1,0 的直线与抛物线E:y2=2px(p>0)交于A,B两点，O为坐标原点，当直线AB垂直
于x轴时，△AOB的面积为 2.
(1)求抛物线E的方程；
(2)若O为△ABC的重心，直线AC,BC分别交y轴于点M,N，记△MCN,△AOB的面积分别为S ,S ，求
1 2
S
1 的取值范围.
S
2
19（. 17分）置换是代数的基本模型，定义域和值域都是集合A=1,2,⋯,n ,n∈N 的函数称为n次置换.满
+
足对任意i∈A,fi =i的置换称作恒等置换.所有n次置换组成的集合记作S n .对于fi ∈S ，我们可用 n
列表法表示此置换：fi
1 2 ⋯ n
=
f1 f2 ⋯ fn
，记fi =f1 i ,f fi =f2 i ,f f2 i =f3 i ,
⋯,f fk-1 i =fk i ,i∈A,k∈N . +
(1)若fi ∈S 4 ,fi
1 2 3 4
= 4 2 1 3 ，计算f3 i ；
(2)证明：对任意fi ∈S 4 ，存在k∈N + ，使得fk i 为恒等置换；
(3)对编号从1到52的扑克牌进行洗牌，分成上下各26张两部分，互相交错插入，即第1张不动，第27张
变为第2张，第2张变为第3张，第28张变为第4张，......，依次类推.这样操作最少重复几次就能恢复原
来的牌型？请说明理由.
·81·湖南省、贵州省 2023-2024 学年高三下学期 2 月开学金太阳联考
数学试题
第I卷(选择题)
一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求
的。
1. 已知a∈R, 若1+i 2-ai 为纯虚数, 则a= ( )
A.-1 B.2 C.-2 D.1
2. 已知集合A= x∣xx-2 >0 ,B={x∈Z∣1<x≤4}, 则A∩B= ( )
A.{2,3} B.{3,4} C.{0,1} D.{1,2}
3. 若直线l:y=kx+1与圆O:x2+y2=1只有一个公共点, 则k= ( )
A.0 B.1 C.-1 D.2
4. 已知向量a=x,1 ,b=4,x , 则“ x>0 ”是“向量a与b的夹角为锐角”的 ( )
A.充要条件 B.充分不必要条件 C.必要不充分条件 D.既不充分也不必要条件
5. 有一组样本数据由5个连续的正整数x ,x ,⋯,x 组成, 其中x 是最小值, x 是最大值, 若在原数据的基
1 2 5 1 5
础上增加两个数据x -1,x +1, 组成一组新的样本数据x -1,x ,x ,⋯,x ,x +1, 则 ( )
1 5 1 1 2 5 5
A.新样本数据的平均数小于原样本数据的平均数
B.新样本数据的平均数大于原样本数据的平均数
C.新样本数据的方差等于原样本数据的方差
D.新样本数据的方差大于原样本数据的方差
6. 大西洋鲑鱼每年都要逆游而上, 游回产地产卵. 研究鲑鱼的科学家发现鲑鱼的游速v(单位:m/s)可以表
O
示为v=klog , 其中O表示鲑鱼的耗氧量的单位数. 若一条鲑鱼游速为0.5 m/s时耗氧量的单位数
3100
为300 , 则一条鲑鱼游速为2 m/s时耗氧量的单位数为 ( )
A.100 B.900 C.1200 D.8100
7.现准备给一半径为6 cm的实心球体玩具制作一个圆台型带盖的纸质包装盒, 要使制成的包装盒能装下
该球体玩具, 且该包装盒的下底面是半径为4 cm的圆, 则制成的包装盒的容积最小为 ( )
·82·A.532πcm3 B.399πcm3 C.266πcm3 D.133πcm3
8. 已知函数fx
x-a
=
ex
的定义域为0,4
x+1
, 若fx 是单调函数, 且fx 有零点, 则a的取值范围是
A. 0,4 B.(0,3] C. 0,2 D.(0,e]
二、选择题：本题共3小题，每小题6分，共18分。在每小题给出的选项中, 有多项符合题目要求。全部选对
的得6分，部分选对的得3分，有选错的得0分。
9. 已知数列a n 的前n项和为S ,a =1,a =a a , 下列结论正确的是 ( ) n 2 m+n m n
A.a =1 B.a =1
2024 2023
C.若S =2024, 则a =1 D.若S =-1, 则a =-1
2024 1 2023 1
10. 已知函数fx
sinxcosx
= , 则下列结论正确的是 ( )
sinx+cosx
A. fx
π
的图象关于直线x= 对称 B. fx
2
3π
的图象关于点 ,0
4
中心对称
C. fx 的最小正周期是2π D. fx
π 3π
在- ,
4 4
2
上有最大值, 且最大值为
4
11. 已知O为坐标原点, P,Q为抛物线C:x2=2pyp>0 上两点, F为C的焦点, 若F到准线的距离为2,则
下列结论正确的是 ( )
A.若M1,3 , 则△PMF周长的最小值为2+ 5
1
B.若直线PQ过点F, 则直线OP,OQ的斜率之积为-
4
C.若N0,-1
QN
, 则 的取值范围是1, 2
QF
9π
D.若△POF的外接圆与准线l相切,则该外接圆的面积为
4
第II卷(非选择题)
三、填空题：本题共3小题，每小题5分，共15分．
12. 甲、乙等7名同学随机站成一排,则甲、乙相邻且甲不站两端的不同排列方式有 种
x2 y2
13. 已知双曲线C: - =1a>0,b>0
a2 b2
的右支上有一点A, 点A关于坐标原点对称的点为B,F为双曲
π
线C的左焦点, 且满足AF⊥BF, 当∠BAF= 时, 双曲线C的离心率为
12
14. 如图, 在三棱锥P-ABC中, 平面PAB⊥平面ABC,PA=2,PB= 7,AB=3,M为棱AB上靠近点B的
三等分点, 且CM为∠ACB的角平分线, 则二面角P-AC-B的平面角的正切值的最小值为 ．
·83·四、解答题：本题共5小题，共77分。解答应写出文字说明、证明过程或演算步骤。
15（. 13分）已知公差不为0的等差数列a n 满足a +a =a +2, 且a ,a ,a 成等比数列. 1 2 3 1 3 7
(1)求a n 的通项公式;
(2)记a n
1
的前n项和为S n ,c n = S +2 , 求数列c n
n
的前n项和T. n
x2 y2
16（. 15分）已知椭圆C: + =1a>b>0
a2 b2
的右顶点为A2,0
1
, 离心率为 .
2
(1)求椭圆C的方程;
12 2
(2)过点A的直线l与椭圆C交于另一点B, 若AB= , 求直线l的方程.
7
7
17（. 15分）如图, 在三棱锥F-ABC中, △ABC是边长为2的等边三角形, FA=FC= , 直线BF与平面
2
ABC所成的角为30°.
(1)证明:BF⊥平面ACF.
(2)求AF与平面BCF所成角的正弦值.
18（. 17分）某学校食堂每天中午为师生提供了冰糖雪梨汤和苹果百合汤, 其均有止咳润肺的功效. 某同学
2
每天中午都会在两种汤中选择一种, 已知他第一天选择冰糖雪梨汤的概率为 , 若前一天选择冰糖雪
3
1
梨汤, 后一天继续选择冰糖雪梨汤的概率为 , 而前一天选择苹果百合汤, 后一天继续选择苹果百合汤
3
1
的概率为 , 如此往复.
2
(1)求该同学第二天中午选择冰糖雪梨汤的概率.
3
(2)记该同学第n天中午选择冰糖雪梨汤的概率为P, 证明: P-
n n 7
为等比数列.
(3)求从第1天到第10天中,该同学中午选择冰糖雪梨汤的概率大于苹果百合汤概率的天数.
19（. 17分）已知函数fx =2ex+ax.
(1)讨论fx 的单调性;
(2)若方程fx =m有两个不相等的根x 1 ,x 2 , 且0<x 1 <x 2 ,fx 的导函数为f x , 证明:f x 1 x 2 <0.
·84··85·河北省 2024 届高三年级大数据应用调研联合测评 (V)
数学试题
第I卷(选择题)
一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求
的。
1.已知复数z满足1-2i
⋅z=i2024(i为虚数单位)，则z= ( )
1+2i 1-2i 1+2i 2i-1
A. B. C.- D.
5 5 5 5
2.已知a,b为平面向量，其中|a|=1,|b|=2,a⋅b=1，则b-2a = ( )
A.1 B.2 C.2 3 D.4
3.德国数学家康托尔在其著作《集合论》中给出正交集合的定义：若集合A和B是全集U的子集，且无公共
元素 ，则称集合 A ､ B 互为正交集合. 规定空集是任何集合的正交集合. 若全集 U =
x∣1<log 2x+1 ≤3,x∈N ,A=x∣x2-7x+10<0,x∈N ，则集合A关于集合U的正交集合B的个
数为 ( )
A.8 B.16 C.32 D.64
4.某小学为提高课后延时服务水平和家长满意度，对该校学生家长就服务质量､课程内容､学生感受､家长
认可度等问题进行随机电话回访.某天共回访5位家长，通话时长和评分情况如下表：
时长x(分钟) 10 12 14 15 19
评分y 60 m 75 1.2m+5 90
根据散点图分析得知y与x具有线性相关关系且求得其回归方程为y=3.2x+29.8，则m= ( )
A.61 B.63 C.65 D.67
5.已知函数 fx = 3cosωx+φ (ω>0)满足对于任意x∈R都有 fx
π
≤ f
3
.若函数 fx 在区间
π π
,
8 2
上有且仅有一个零点，则ω的最大值为 ( )
21 15
A.3 B. C. D.5
4 4
1 3 2 3
6.已知a､b均为正实数，且满足 + =2，则 + 的最小值为 ( )
a b 2a-1 2b-3
A.2 B.2 2 C.2 3 D.2 6
7.陀螺是中国传统民俗体育游戏，流传甚广，打陀螺已被列入第五批国家级非物质文化遗产代表性项目名
录.陀螺结构分为上下两部分：上部分为木质件，下部分为球形钢珠.其中木质件的形状为上部是底面半
径为2.2cm，高为1.63cm的圆柱，下部为上底半径为2.2cm，下底半径为0.21cm，高为0.78cm的圆台.若
陀螺的木质件由一个球形原料经车床一次性车制而成，那么原料的半径最小为 ( )
·86·A.2.21cm B.2.22cm C.2.23cm D.2 2cm
8.已知圆C :x2+y2=4上有一动点P，圆C :(x-2)2+(y-3)2=1上有一动点Q，直线l:x-y+3=0上有一
1 2
动点M，直线PM与圆C 1 相切，直线QM与圆C 2 相切，则PM +QM 的最小值为 ( )
A.4 B.5 C.2 6 D. 14+ 2
二、选择题：本题共3小题，每小题6分，共18分。在每小题给出的选项中, 有多项符合题目要求。全部选对
的得6分，部分选对的得3分，有选错的得0分。
π
9.已知α,β∈0,
2
,cosα+β
5
= ,sinα-β
13
3
= ，则 ( )
5
A.sinα+β
12
= B.cosα-β
13
4 63 tanα 33
=- C.sin2α= D. =
5 65 tanβ 7
10.双曲抛物面又称马鞍面，其形似马具中的马鞍表面而得名.其在力学､建筑学､美学中有着广泛的应用.在
空间直角坐标系中，将一条xOz平面内开口向上的抛物线沿着另一条yOz平面内开口向下的抛物线滑
x2
动(两条抛物线的顶点重合)所形成的就是马鞍面，其坐标原点被称为马鞍面的鞍点，其标准方程为
a2
y2
- =2z(a>0,b>0)，则下列说法正确的是 ( )
b2
A.用平行于xOy平面的面截马鞍面，所得轨迹为双曲线
B.用法向量为1,0,0 的平面截马鞍面所得轨迹为抛物线
C.用垂直于y轴的平面截马鞍面所得轨迹为双曲线
D.用过原点且法向量为1,1,0 的平面截马鞍面所得轨迹为抛物线
11.已知函数fx 是定义在R上的连续可导函数，且满足①f2-x -fx =2x3-6x2+12x-8；②fx 为
奇函数，令gx =fx +x3，则下列说法正确的是 ( )
A. gx 的图象关于x=1对称 B. f 1 =-3
·87·C. f2024 =20243 D. f 2023 =-3×20232
第II卷(非选择题)
三、填空题：本题共3小题，每小题5分，共15分．
12.已知(x+2)4 2x2+3x =a +a x+a x2+⋯+a x6，则a = .
0 1 2 6 4
x2 y2
13.已知椭圆 + =1(a>b>0)的左､右焦点分别为F ､F，点P为第一象限内椭圆上一点，△FPF 的
a2 b2 1 2 1 2
内心为I1, 3 ，且∠FPI=30°，则椭圆的离心率为 . 1
14.已知数列a n
1 1
满足a 1 =2，且a n+1 =a2 n +4a n +2，则a n = ；令b n = a +3 + a +1 ，若b n
n n+1
的前n项和
为S ，则S = .
n n
四、解答题：本题共5小题，共77分。解答应写出文字说明、证明过程或演算步骤。
15（. 13分）已知函数fx
m 1
=lnx+ - (m>0).
x2 2
(1)当m=1时，求曲线y=fx 在点 1,f1 处的切线方程；
(2)若fx
1
≥ 恒成立，求实数m的取值范围.
2
x2 y2
16（. 15分）已知双曲线C: - =1(a>0,b>0)的右焦点F到一条渐近线的距离为1，且双曲线左支上
a2 b2
任意一点M到F的距离的最小值为2+ 3.
(1)求双曲线C的方程；
(2)已知直线l:y=kx+1交C于A､B两点，O为坐标原点，若OA⋅OB=10，求直线l的斜率k的值.
17（. 15分）已知在多面体PQABCD中，平面PADQ⊥平面ABCD，四边形ABCD为梯形，且AD∥BC，四边
形PADQ为矩形，其中M和N分别为AD和AP的中点，AB= 7,BC=5,AD=DC=2.
(1)证明：平面BMN⊥平面QDC；
5
(2)若二面角N-BM-C的余弦值为- ，求直线BQ与平面BMN所成角的正弦值.
5
18（. 17分）现有红､绿､蓝三种颜色的箱子，其中红箱中有4个红球，2个绿球，2个蓝球；绿箱中有2个红球，
4个绿球，2个蓝球；蓝箱中有2个红球，2个绿球，4个蓝球.所有球的大小､形状､质量完全相同.第一次
从红箱中随机抽取一球，记录颜色后将球放回去；第二次要从与第一次记录颜色相同的箱子中随机抽取
一球，记录颜色后将球放回去；以此类推，第k+1次是从与第k次记录颜色相同的箱子中随机抽取一球，
记录颜色后放回去.记第n次取出的球是红球的概率为P，
n
(1)求第3次取出的球是蓝球的概率；
·88·(2)求P 的解析式
n
19（. 17分）设a,b为非负整数，m为正整数，若a和b被m除得的余数相同，则称a和b对模m同余，记为a≡
bmodm .
(1)求证：233+1≡65mod7 ；
(2)若p是素数，n为不能被p整除的正整数，则np-1≡1modp ，这个定理称之为费马小定理.应用费马
小定理解决下列问题：
①证明：对于任意整数x都有x13-x≡0mod546 ；
②求方程x9+x7-x3-x≡0mod35 的正整数解的个数.
·89·安徽省 1 号卷 A10 联盟 2024 届高三开年考
数学试题
第I卷(选择题)
一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求
的。
1.已知向量a=(m,2),b=(1,-4)，若a⎳b，则实数m的值为 ( )
1
A.- B.-2 C.-1 D.8
2
3
2.复数z=i+ 在复平面内对应的点位于 ( )
1-i3
A.第一象限 B.第二象限 C.第三象限 D.第四像限
3.已知直线l与曲线fx =ex+sinx在点 0,f0 处的切线垂直，则直线l的斜率为 ( )
1
A.-1 B.1 C.- D.2
2
4.已知正项数列a n
n+1 a
满足a = a ，则 8 = ( ) n+1 2n n a
4
1 1 1 1
A. B. C. D.
16 8 4 2
5.已知抛物线C:x2=2py(p>0)的准线为y=-2，点P,Q在抛物线C上，且线段PQ的中点为-2,4 ，则直
线PQ的方程为 ( )
A. x+2y-6=0 B. x+3y-10=0 C.2x+y=0 D.2x+3y-8=0
6.近期，哈尔滨这座“冰城”火了，2024年元旦假期三天接待游客300多万人次，神秘的鄂伦春族再次走进
世人的眼帘，这些英雄的后代讲述着英雄的故事，让哈尔滨大放异彩．现安排6名鄂伦春小伙去三个不
同的景点宣传鄂伦春族的民俗文化，每个景点至少安排1人，则不同的安排方法种数是 ( )
A.240 B.420 C.540 D.900
7.如图，AB为圆锥SO底面圆的一条直径，点C为线段SA的中点，现沿SA将圆锥SO的侧面展开，所得的
平面图形中△ABC为直角三角形，若SA=4，则圆锥SO的表面积为 ( )
32π 16π
A. B. C.8π D.12π
9 9
·90·8.“曼哈顿距离”是人脸识别中的一种重要测距方式，其定义如下：设Ax 1 ,y 1 ,Bx 2 ,y 2 ，则A,B两点间的曼
哈顿距离dA,B =x 1 -x 2 +y -y 1 2 ，已知M4,6 ，点N在圆C:x2+y2+6x+4y=0上运动，若点P满足
d(M,P)=2，则PN 的最大值为 ( )
17 2
A.7 3+ 13 B. + 13 C. 145+ 13 D. 149+ 13
2
二、选择题：本题共3小题，每小题6分，共18分。在每小题给出的选项中, 有多项符合题目要求。全部选对
的得6分，部分选对的得3分，有选错的得0分。
9.已知函数fx
1 π
=2sin x-
3 4
，则 ( )
9π
A.直线x= 为fx
4
图象的一条对称轴
3π
B.点- ,0
4
为fx 图象的一个对称中心
C.将fx
3π
的图象向右平移 个单位长度后关于y轴对称
4
D. fx 在π,3π 上单调递增
10.已知棱长为2的正方体ABCD-A B C D 中，动点M在棱DD 上，记平面BC M截正方体所得的截面图
1 1 1 1 1 1
形为Ω，则 ( )
A.平面A BC⊥平面B C D B.不存在点M，使得直线CM⎳平面BA C
1 1 1 1 1
C. B M+CM的最小值为2 4+2 2 D.Ω的周长随着线段DM长度的增大而增大
1
11.已知函数 fx ,gx 的定义域均为R，其中 fx 的图象关于点1,1 中心对称，gx 的图象关于直线x
=2对称，fx -g2+x =4,g2 =3，则 ( )
A. f-x +fx =0 B. f2024 =7 C. g2024
2024
=-1 D.f(k)=2024
k=1
第II卷(非选择题)
三、填空题：本题共3小题，每小题5分，共15分．
12.已知集合M= x∈N∣x+2 x-3 <0 ,N=-2,-1,0,1,2 ，则M∩N= ．
π
13.在△ABC中，AC=4，且sinB=2sinAsinC，则△ABC的面积为 ；若C= ，则B= ．
4
x2 y2
14.已知椭圆C: + =1(a>b>0)的左､右焦点分别为F ,F ，过F 的直线与C交于M,N两点，若
a2 b2 1 2 1
3S =7S ，且∠FFN=∠FNF，则C的离心率为 ．
△MNF2 △MF1F2 2 1 2 1
四、解答题：本题共5小题，共77分。解答应写出文字说明、证明过程或演算步骤。
15（. 13分）2023年12月28日，小米汽车举行了技术发布会，首款产品SU7揭开神秘面纱，引起了广大车迷
爱好者的热议，为了了解车迷们对该款汽车的购买意愿与性别是否具有相关性，某车迷协会随机抽取了
200名车迷朋友进行调查，所得数据统计如下表所示．
性别 购车意愿 合计
·91·愿意购置该款汽车 不愿购置该款汽车
男性 100 20 120
女性 50 30 80
合计 150 50 200
(1)请根据小概率值α=0.001的独立性检验，分析车迷们对该款汽车的购买意愿与性别是否有关；
(2)用频率估计概率，随机抽取两名车迷作深度访谈，记其中愿意购置该款汽车的人数为X，求X的分布
列与期望．
n(ad-bc)2
参考公式：χ2=
a+b c+d a+c b+d
，其中n=a+b+c+d．
α 0.1 0.05 0.01 0.005 0.001
2.70
x 3.841 6.635 7.879 10.828
α
6
16（. 15分）如图，在正四棱锥S-ABCD中，SA=AB= 2，点O是AC的中点，点P在棱SD上(异于端点)．
(1)若点P是棱SD的中点，求证：平面SAD⊥平面PAC；
5
(2)若二面角S-AC-P的余弦值为 ，求线段SP的长．
5
x2 y2
17（. 15分）已知双曲线C: a2 - b2 =1(a>0,b>0)的左､右焦点分别为F 1 ,F 2 ，点A- 6, 2 在C上，且
△AFF 的面积为 6．
1 2
(1)求双曲线C的方程；
1
(2)记点A在x轴上的射影为点B，过点B的直线l与C交于M,N两点．探究：
BM
1
+
2 BN
是否为定
2
值，若是，求出该定值；若不是，请说明理由．
18（. 17分）已知函数fx =xk+1 lnx-λx ，其中k,λ∈R．
(1)若k=-1，讨论fx 在1,4 上的单调性；
(2)若存在正数k，使得∀x 1 ,x 2 ∈0,+∞ ，且x ≠x 时， fx 1 1 2 -fx 2 <0，求λ的取值范围． x -x
1 2
19（. 17分）基本不等式可以推广到一般的情形：对于n个正数a ,a ,⋯,a ，它们的算术平均不小于它们的几
1 2 n
a +a +⋯+a
何平均，即 1 2 n n ≥ na 1 a 2 ⋯a n ，当且仅当a 1 =a 2 =⋯=a n 时，等号成立．若无穷正项数列a n 同
时满足下列两个性质：①∃M>0,a n <M；②a n 为单调数列，则称数列a n 具有性质P．
·92·4
(1)若a n =n+ n2 ，求数列a n 的最小项；
1 n
(2)若b n = 2n-1 ，记S n =b n ，判断数列S n
i=1
是否具有性质P，并说明理由；
1
(3)若c =1+ n n
n
，求证：数列c n 具有性质P．
·93·黑龙江省“六校联盟” 2023 - 2024 学年高三下学期联合性适应
测试数学试题
第I卷(选择题)
一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求
的。
1.已知集合P=1,2 ，Q=2,3 ，若M=xx∈P,x∉Q ，则M= ( )
A. 1 B. 2 C. 1,3 D. 1,2,3
2.在正项等比数列a n 中，S 为其前n项和，若S =10，S =30，则S 的值为 ( ) n 10 20 30
A.50 B.70 C.90 D.110
π
3.已知α∈0,
2
π
，且cosα-
4
= 3cos2α，则sin2α= ( )
5 1 1 5
A.- B.- C. D.
6 6 6 6
4.已知a、b为单位向量，且a-2b
=a+b
，则a、b的夹角为 ( )
π π 2π 5π
A. B. C. D.
6 3 3 6
5.已知F为抛物线C:y2=2pxp>0 的焦点，过F且斜率为1的直线交C于A,B两点，若FA ⋅FB =2，
则p= ( )
A.1 B.2 C.3 D.4
6.“曼哈顿距离”是由十九世纪的赫尔曼．闵可夫斯基所创词汇，是种使用在几何度量空间的几何学用语，
即对于一个具有正南正北、正东正西方向规则布局的城镇街道，从一点到达另一点的距离是在南北方向
上旅行的距离加上在东西方向上旅行的距离，“欧几里得距离(简称欧氏距离)”是指平面上两点的直线
距离，如图a所表示的就是曼哈顿距离，b所表示的就是欧氏距离，若Ax 1 ,y 1 、Bx 2 ,y 2 ，则两点的曼哈
顿距离DA,B =x 1 -x 2 +y -y 1 2 ，而两点的欧氏距离为dA,B = x 1 -x 2 2+y 1 -y 2 2，设点O0,0 ，在
平面内满足dM,O ≤1的点组成的图形面积记为S 1 ，DM,O ≤1的点组成的图形面积记为S ，则 2
S 1 -S 2 = ( )
A.0 B.π-2 C.π-1 D.4-π
7.已知a=20232022，b=20242023，c=20252024，则 ( )
·94·A.a>c>b B.b>a>c C.a>b>c D.b>c>a
8.以正方体ABCD-A B C D 的8个顶点中的某4个为顶点可组成一个三棱锥，在所有这些三棱锥中任取
1 1 1 1
一个，则该三棱锥各个面都不为直角三角形的概率为 ( )
1 1 2 3
A. B. C. D.
58 29 29 29
二、选择题：本题共3小题，每小题6分，共18分。在每小题给出的选项中, 有多项符合题目要求。全部选对
的得6分，部分选对的得3分，有选错的得0分。
π
9.已知直线x= 是函数f(x)=sin(2x+φ)(0<φ<π)图象的一条对称轴，则 ( )
8
π
A. fx+
8
3π
是偶函数 B. x= 是f(x)图象的一条对称轴
8
π π
C. f(x)在 ,
8 2
π
上单调递减 D.当x= 时，函数f(x)取得最小值
2
10.已知A2,0 、B4,1 ，点Mx,y 为曲线C上动点，则下列结论正确的是 ( )
A.若C为抛物线y2=8x，则 MA +MB =2+ 17 min
x2 y2
B.若C为椭圆 + =1，则 MA 25 21 +MB =10- 37 min
y2
C.若C为双曲线x2- =1，则 MA 3 +MB = 37-2 min
1
D.若C为圆x2+y2=1，则 MA
2
+MB
53
=
2
min
11.容器中有A、B、C3种颜色的小球，若相同颜色的两颗小球发生碰撞，则变成一颗B球；不同颜色的两颗
小球发生碰撞，会变成另外小球． 例如，一颗A球和一颗B球发生碰撞则变成一颗C球，现有A球10
颗，B球8颗，C球9颗，如果经过各种两两碰撞后，只剩1颗球． 则下列结论正确的是 ( )
A.一定经过了26次碰撞 B.最后一颗球可能是A球
C.最后一颗球可能是B球 D.最后一颗球可能是C球
第II卷(非选择题)
三、填空题：本题共3小题，每小题5分，共15分．
12.复数1+2i 3的实部与虚部的和为 ．
13.某中学共有学生600人，其中男生400人，女生200人．为了获得该校全体学生的身高信息，采用男、女
按比例分配的分层随机抽样的方法抽取样本，并观测样本的指标值(单位：cm)，经计算得到男生样本的
均值为170，方差为18，女生样本的均值为161，方差为30．根据以上数据，估计该校全体学生身高的均
值为 ；估计该校全体学生身高的方差为 ．
14.已知正三棱锥的各顶点都在表面积为64π球面上，正三棱锥体积最大时该正三棱锥的高为 .
四、解答题：本题共5小题，共77分。解答应写出文字说明、证明过程或演算步骤。
15（. 13 分）已知在锐角三角形 △ABC 中，边 a，b，c 对应角 A,B,C，向量 m = 2cosA, 3
，n =
·95·π
sinA-
3
,cos2A
，且m与n垂直，c=2．
(1)求角A；
(2)求a+b的取值范围．
16（. 15分）已知数列a n
2a +1, n=2k-1
的前n项和为S n ，满足a 1 =1，a n+1 = n k∈N∗
3a +2, n=2k
n
．
(1)若数列b n 满足b n =a 2n-1n∈N∗ ，求b n 的通项公式；
(2)求数列a n 的通项公式，并求S ． 2n
17（. 15分）已知：斜三棱柱ABC-A B C 中，BB ⊥AC，AA 与面ABC所成角正切值为2，AA = 5，AB=
1 1 1 1 1 1
2
BC= AC=2 2，点E为棱A C 的中点，且点E向平面ABC所作投影在△ABC内．
2 1 1
(1)求证：AC⊥EB；
AF
(2)F为棱AA 上一点，且二面角A-BC-F为30°，求 的值．
1 AA
1
x2 y2
18（. 17分）已知椭圆C： + =1a>b>0
a2 b2
过点2,0
1
，且离心率为 ，过右焦点F的直线交椭圆C于
2
M、N两点，直线l:x=4交x轴于P，过M、N分别作l的垂线，交l于S、T两点，H为l上除点P的任一
点．
(1)求椭圆C的方程；
(2)求S △MPN 2-4S ⋅S 的值； △MPS △NPT
k +k
(3)设直线HM、HN、HF的斜率分别为k 、k 、k ，求 HM HN 的值．
HM HN HF k
HF
19（. 17分）设函数fx =ex，gx =lnx.
(1)已知ex≥kx≥lnx对任意x∈0,+∞ 恒成立，求实数k的取值范围；
(2)已知直线l与曲线fx 、gx 分别切于点 x 1 ,fx 1 、x 2 ,gx 2 ，其中x >0 1
·96·①求证：e-2<x <e-1；
2
②已知λx 2 -x+1 ex+x≤0对任意x∈x 1 ,+∞ 恒成立，求λ的取值范围．
·97·安徽省六校教育研究会 2023 - 2024 学年高三下学期下学期第
二次素养测试 (2 月) 数学试题
第I卷(选择题)
一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求
的。
x-1
1.已知全集U=R，集合M=x <0 x+3 ，N=y∈Ry= x+1 ，则M∩N等于 ( )
A. -1,1 B. 0,1 C. -3,0 D. -3,-1
2.若1-i z=2i，则z-2i = ( )
A.0 B.1 C. 2 D.2
3.(1-ax)6的展开式中x3的系数为160，则a= ( )
A.2 B.-2 C.4 D.-4
在发生某公共卫生事件期间，有专业机构认为该事件在一段时间没有发生在规模群体感染的标志为“连
4.续10天，每天新增疑似病例不超过7人”.根据过去10天甲、乙、丙、丁四地新增疑似病例数据，一定符
合该标志的是
A.甲地：总体均值为3，中位数为4 B.乙地：总体均值为1，总体方差大于0
C.丙地：中位数为2，众数为3 D.丁地：总体均值为2，总体方差为3
x2 y2
5.椭圆 + =1经过点2,3
a2 a2-4
，则其离心率e= ( )
1 2 3 3
A. B. C. D.
2 2 2 3
6.若函数 f x
π
= sinωx-
3
ω>0 在区间 0,π 恰存三个零点，两个极值点，则 ω 的取值范围是
( )
7 17
A. ,
3 6
11 7
B. ,
6 3
11 17
C. ,
6 6
7 20
D. ,
3 6
7.已知棱长为8的正四面体，沿着四个顶点的方向各切下一个棱长为2的小正四面体(如图)，剩余中间部
分的八面体可以装入一个球形容器内(容器壁厚度忽略不计)，则该球形容器表面积的最小值为
( )
·98·A.12π B.24π C.36π D.48π
8.已知函数 f(x)=a2e2x-xlnx+xlna(a>0)，若方程 fx =0有两个不同的实数解，则实数a的取值范围
是 ( )
1
A. 0,
e
1
B. 0,
c
1
C. ,1
e
1
D. ,1
e
二、选择题：本题共3小题，每小题6分，共18分。在每小题给出的选项中, 有多项符合题目要求。全部选对
的得6分，部分选对的得3分，有选错的得0分。
9.已知等差数列a n 的前n项和为S n ,a 1 >0，且S 11 -S 7 S 11 -S 8 <0，则 ( )
A.a +a >0 B.S <S <S
9 10 7 11 8
C.当n=10时，S 取最大值 D.当S <0时，n的最小值为19
n n
10.已知直线l:a+2 x-a+1 y-1=0与圆C:x2+y2=4交于点A,B，点P1,1 ,AB中点为Q，则 ( )
A. AB 的最小值为2 2 B. AB 的最大值为4
C. PA⋅PB为定值 D.存在定点M，使得MQ 为定值
11.已知函数fx ,gx 的定义域均为R，f1-x +g1+x =2，gx -fx-2 =2，g4-x -fx =2，
且当x∈0,1 时．fx =x2+1，则 ( )
A. g2024
2024
=2 B.g(i)=0
i=1
C.函数fx 关于直线x=3对称 D.方程fx+2024 =x有且只在2个实根
第II卷(非选择题)
三、填空题：本题共3小题，每小题5分，共15分．
12.抛物线C:y2=8x的焦点为F，过F的直线l与曲线C交于A,B两点，点 A的横坐标为6,则 AB =
．
13.已知正方形ABCD的边长为2，中心为O，四个半圆的圆心地为正方形ABCD各边的中点(如图)，若P在
BC上，且AP=λAB+μAD，则λ+μ的最大值为 ．
·99·14.设S 是以定点P 为球心半径为r的球面，π 是一个固定平面，P 到π 的距离为a,a>r．设S 是以点M
0 0 0 0 0 M
为球心的球面，它与S 外切并与π 相切．令A为满足上述条件的球心M构成的集合．设平面π与π 平
0 0 0
行且在π上有A中的点．设d 是平面π与π 之间的距离．则d 的最小值为 ．
∑ 0 ∑
四、解答题：本题共5小题，共77分。解答应写出文字说明、证明过程或演算步骤。
π
15（. 13分）在△ABC中，内角A,B,C的对边分別为a,b,c，sinB+
6
a+b
= .
2c
(1)求角C；
(2)若a+b=2 3,c= 6，求角C的平分线CD的长度.
16（. 15分）如图，四棱锥E-ABCD的底面ABCD是菱形，点F,G分别在棱CD,BE上，BG=2GE,CF=2FD,
EA=ED=AD=BD=2．
(1)证明：FG⎳平面ADE；
(2)若二面角E-AD-B大小为120°，求FG与平面BCE所成角的正弦值．
17（. 15分）(1)已知x>0，证明：1+x<ex<(1+x)1+x；
n nn
(2)证明：(n-k)n< n∈N*
e-1
k=1
．
18（. 17分）某学校有甲、乙、丙三家餐厅，分布在生活区的南北两个区域，其中甲、乙餐厅在南区，丙餐厅在北
区各餐厅菜品丰富多样，可以满足学生的不同口味和需求．
(1)现在对学生性别与在南北两个区域就餐的相关性进行分析，得到下表所示的抽样数据，依据α=
0.100的独立性检验，能否认为在不同区域就餐与学生性别有关联？
就餐区域
性别 合计
南区 北区
男 33 10 43
女 38 7 45
合计 71 17 88
·100·1
(2)张同学选择餐厅就餐时，如果前一天在甲餐厅，那么后一天去甲，乙餐厅的概率均为 ；如果前一天
2
1 2
在乙餐厅，那么后一天去甲，丙餐厅的概率分别为 ， ；如果前一天在丙餐厅，那么后一天去甲，乙餐厅
3 3
1 1 1 1
的概率均为 ．张同学第1天就餐时选择甲，乙，丙餐厅的概率分别为 ， ， ．
2 4 4 2
(ⅰ)求第2天他去乙餐厅用餐的概率；
(ⅱ)求第nn∈N* 天他去甲餐厅用餐的概率p ．
n
n(ad-bc)2
附：χ2=
a+b c+d a+c b+d
,n=a+b+c+d；
0.10
α 0.050 0.025 0.010
0
2.70
x 3.841 5.024 6.635
α
6
19（. 17分）已知点F 1-2,0 ,F 22,0 ,M是圆O:x2+y2=1上任意一点，点F 关于点M的对称点为N，线段FN 1 1
的中垂线与直线FN相交于点T，记点T的轨迹为曲线C．
2
(1)求曲线C的方程；
(2)若点A1,0 ,H1,1 ，直线l:x=2，过点H的直线l 与C交于D、E两点，直线AD、AE与直线l分别交 1
于点P、Q．证明：PQ的中点为定点．
·101·浙江省新阵地教育联盟 2024 届高三下学期第三次联考 (开学
考试) 数学试题
第I卷(选择题)
一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求
的。
1.已知复数z满足1+2i z=4+3i，则z的虚部是 ( )
A.-1 B.1 C.-i D.i
2.设集合A= y
1
y=log x,x>
2 2
，B= y
1
y= ,x>0
2x
，则 ( )
A. A∩B=-1,1 B. A∪B=B
C. A∩∁ R B =1,+∞ D. A∩B=B
3.已知fx =3x+1 x-a 3x-1 +log x2+1-x 3 是奇函数，则常数a= ( )
A.-2 B.-1 C.0 D.1
4.在正方体ABCD-A B C D 中，E,F分别为AB,BC的中点，则 ( )
1 1 1 1
A.平面B EF∥平面A C D B.平面B EF⊥平面BC D
1 1 1 1 1
C.平面B EF∥平面A CC D.平面B EF⊥平面B DD
1 1 1 1 1 1
5.袋子中装有3个红球和4个蓝球，甲先从袋子中随机摸一个球，摸出的球不再放回，然后乙从袋子中随机
摸一个球，若甲､乙两人摸到红球的概率分别为p ,p ，则 ( )
1 2
A. p =p B. p <p C. p >p D. p >p 或p <p
1 2 1 2 1 2 1 2 1 2
2 2
6.在平行四边形ABCD中，点E是AB的中点，点F,G分别满足AF= AD,BG= BC，设AB=a,AD=
3 3
b，若EF⊥EG，则 ( )
3
A.|b|= |a| B. b
4
=a
3
C.|b|= |a| D.|b|=2|a|
2
7.已知正项等差数列a n 的前n项和为S ，则“2a +a =a”是“ S n 1 2 3 n 为等差数列”的 ( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
x2 y2
8.双曲线 - =1(a,b>0)的左右焦点分别为F,F,P是双曲线右支上一点，点F 关于∠FPF 平分线
a2 b2 1 2 1 1 2
1
的对称点也在此双曲线上，且cos∠FPF= ，则双曲线的离心率为 ( )
1 2 9
21 21
A. B. C. 2 D. 3
4 3
二、选择题：本题共3小题，每小题6分，共18分。在每小题给出的选项中, 有多项符合题目要求。全部选对
·102·的得6分，部分选对的得3分，有选错的得0分。
9.如图，八面体的每个面都是正三角形，并且4个顶点A,B,C,D在同一个平面内，如果四边形ABCD是边
长为2的正方形，则 ( )
π 1
A.异面直线AE与DF所成角大小为 B.二面角A-EB-C的平面角的余弦值为
3 3
8π
C.此八面体一定存在外接球 D.此八面体的内切球表面积为
3
π
10.函数f(x)=2cos(ωx+φ)ω>0,|φ|<
2
5π
相邻两个最高点之间的距离为π, ,0
12
为f(x)的对称中心，
π
将函数f(x)的图象向左平移 后得到函数y=g(x)的图象，则 ( )
12
5π
A. g(x)在0,
12
上存在极值点
1 π
B.方程g(x)= x-
2 3
4π
所有根的和为
3
π
C.若g(x+m)为偶函数，则正数m的最小值为
12
λ
D.若g x
2
π π
在 ,
3 2
4
上无零点，则正数λ的取值范围为0,
3
16
∪ 5,
3
11.在平面直角坐标系中，如果将函数y=fx
π
的图象绕坐标原点逆时针旋转α(0<α≤ ,α为弧度)后，所
2
得曲线仍然是某个函数的图象，则称fx 为“α旋转函数”，则 ( )
π
A.∀α∈0,
2
，函数y=x都为“α旋转函数”
B.若函数fx =sinx,x∈0,π
π
为“α旋转函数”，则α∈0,
4
C.若函数gx
2 π
=ax- 为“ 旋转函数”，则a=1
x 4
D.当m≤-2e2或m≥1时，函数hx
π
=mxex+1不是“ 旋转函数”
4
第II卷(非选择题)
三、填空题：本题共3小题，每小题5分，共15分．
12.有甲乙两生从“物理､化学､生物､政治､历史､地理和技术”七门科目中选三门作为高考选考科目，学生甲
物理和化学两门必选，并在另外的五门中任选一门；学生乙必选政治学科，但一定不选物理､化学，则甲乙
两人有且只有一门选科相同的选科方法总数有 种.(用数字作答)
13.P是圆C:x2+(y-2)2=1上一动点，A2,0 ,Q为AP的中点，O为坐标原点，则OQ 的最大值为 .
·103·14.已知函数 fx 满足 fx = f1-x ,f x 为 fx 的导函数，gx = f x
1 n
+ ,x∈R.若a =g 3 n 2024 ，
则数列a n 的前2023项和为 .
四、解答题：本题共5小题，共77分。解答应写出文字说明、证明过程或演算步骤。
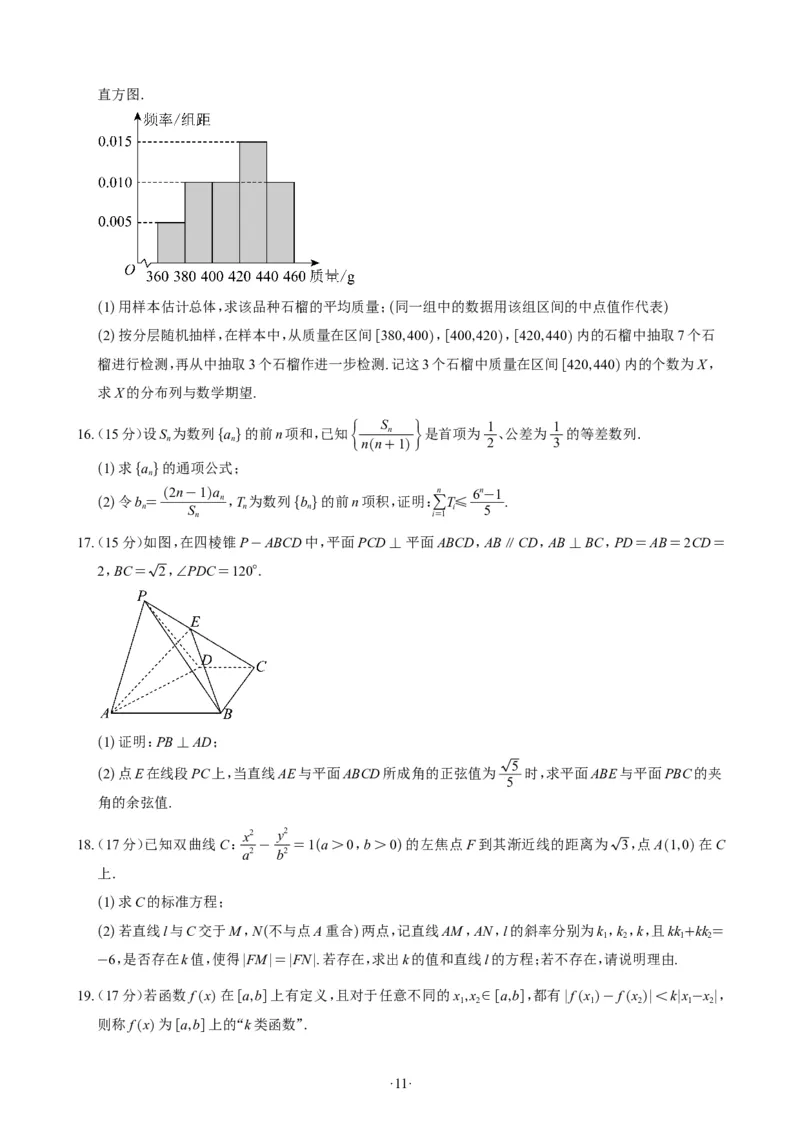
15（. 13分）某校为了解本校学生课间进行体育活动的情况，随机抽取了120名男生和120名女生，通过调查
得到以下数据：120名女生中有20人课间经常进行体育活动，120名男生中有40人课间经常进行体育
活动.
(1)完成如下列联表(单位：人)，并判断能否有99.5%的把握认为学生课间经常进行体育活动与性别有关
联.
课间进行体育活动情况
性别 合计
不经常 经常
男
女
合计
(2)以样本的频率作为概率的值，在全校的学生中任取3人，记其中课间经常进行体育活动的人数为X，
求X的分布列与数学期望.
n(ad-bc)2
附：χ2=
a+b c+d a+c b+d
，其中n=a+b+c+d.
α 0.100 0.050 0.010 0.005 0.001
x 2.706 3.841 6.635 7.879 10.828
α
16（. 15分）记△ABC的内角A,B,C所对的边分别是a,b,c，且满足2sinC=3sinA-B .
(1)证明：tanA=5tanB；
5
(2)若△ABC的面积为 c2，求tanC；
12
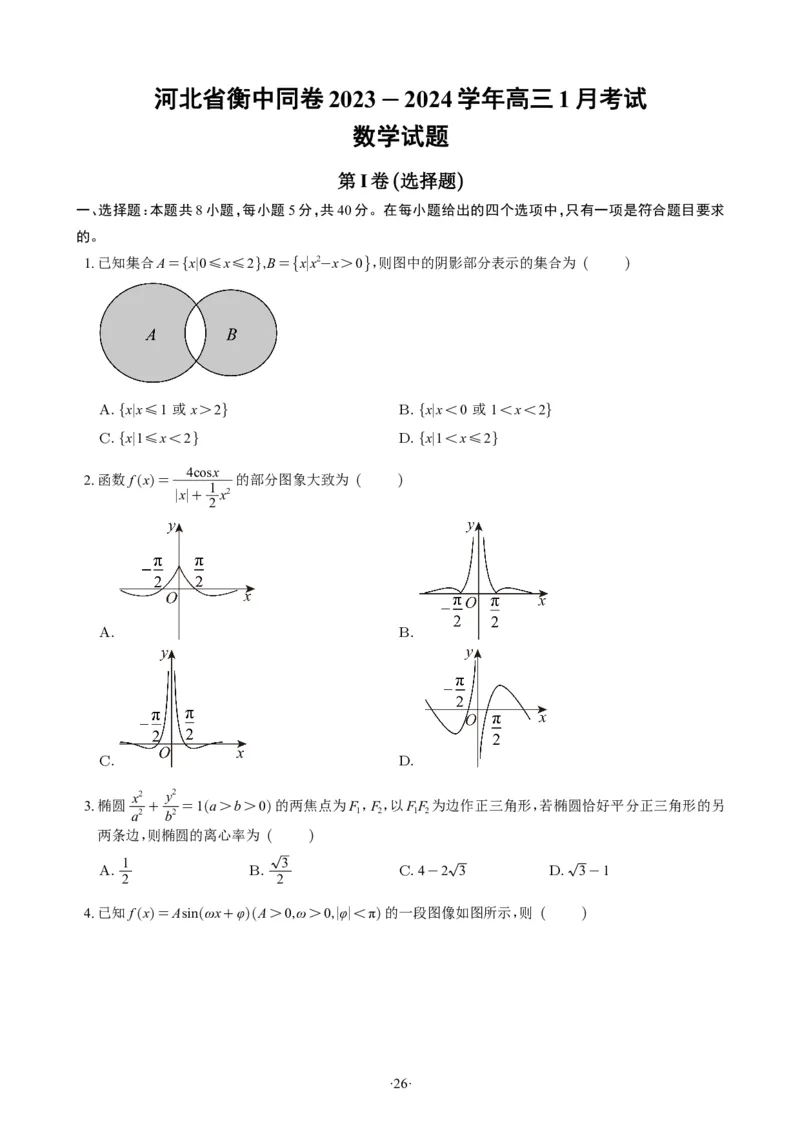
17（. 15分）在三棱锥D-ABC中，AC=3,DC=2 2,∠DCA=45°,CB⊥AB,BC=BD= 6.
(1)证明：平面ADC⊥平面ABC；
33
(2)点E为棱DC上，若BC与平面EAB所成角的正弦值为 ，求DE的长；
11
x2 y2 1
18（. 17分）已知椭圆 + =1(a>b>0)的长轴长为4，离心率为 ，左顶点为C，过右焦点F作直线与
a2 b2 2
椭圆分别交于A,B两点(异于左右顶点)，连接AC,CB.
(1)证明：AC与AF不可能垂直；
·104·(2)求|AB|2+|BC|2+|CA|2的最小值；
19（. 17分）已知函数fx =cosx+λln1+x ，且曲线y=fx 在点 0,f0 处的切线斜率为1.
(1)求fx 的表达式；
(2)若fx ≤ax+1恒成立，求a的值.
2n 1
(3)求证：∑ fsin -1
k
k=n+1
<ln2,n∈N*.
·105·河北省百师联盟 2024 届高三下学期开学摸底联考
数学试题
第I卷(选择题)
一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求
的。
1
1.已知集合A=xx2- ≤0
4
1
,B=x ≥1
x
，则A∩B= ( )
1
A. 0,
2
1
B. 0,
2
C. 0,1 D. 0,1
3-2ai
2.复数z= a∈R
2i
在复平面内对应的点在 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.命题“∀x<-1,log x2>0”的否定为 ( )
2
A.∀x<-1,log x2≤0 B.∀x≥-1,log x2>0
2 2
C.∃x≥-1,log x2>0 D.∃x<-1,log x2≤0
2 2
x2 y2
4.若双曲线 - =1(a>0,b>0)的实轴长为2，离心率为 3，则双曲线的左焦点F到一条渐近线的距
a2 b2
离为 ( )
A. 2 B.2 2 C.1 D.2
5.已知上底面半径为 2，下底面半径为2 2的圆台存在内切球(与上、下底面及侧面都相切的球)，则该圆
台的体积为 ( )
14 6π 56π
A.14 6π B.56π C. D.
3 3
6.已知实数m,n满足1>m>n>0，设a=mlnn,b=nlnm,c=nlnn，则 ( )
A.a=b>c B.a>b>c C.c>a>b D.c>a=b
2π
7.在△ABC中，D为边BC上一点，∠DAC= ,AD=4,AB=2BD，且△ADC的面积为4 3，则sin∠ABD
3
= ( )
15- 3 15+ 3 5- 3 5+ 3
A. B. C. D.
8 8 4 4
8.已知等差数列a n
2n2 2m2
的前n项和为S ，若m≠n，且a +a = ,a +a = ，则S = ( ) n 1 m m 1 n n m+n
A.(m+n)2 B.-(m+n)2 C.m2-n2 D.n2-m2
二、选择题：本题共3小题，每小题6分，共18分。在每小题给出的选项中, 有多项符合题目要求。全部选对
的得6分，部分选对的得3分，有选错的得0分。
·106·9.下列说法正确的是 ( )
A.若随机变量X∼B2,0.2 ，则PX=2 =0.2
B.若经验回归方程y=bx+a中的b>0，则变量x与y正相关
C.若随机变量ξ∼N0,σ2
1
，且Pξ<-
2
1
=p，则P0<ξ<
2
1
= -p
2
D.若事件A与B为互斥事件，则A的对立事件与B的对立事件一定互斥
10.已知函数fx
x
=2sinxcos2 ，则以下结论正确的是 ( )
2
A.π为fx 的一个周期 B. fx
π 3π
在- ,
2 2
上有2个零点
C. fx
π
在x=- 3 处取得极小值 D.对∀x 1 ,x 2 ∈R, fx 2 -fx 1 ≤ 3
11.已知定义在R上的函数y=f2x+2
1
为奇函数，且对∀x∈R，都有fx+
2
3
=f -x
2
，定义在R上
的函数f x 为fx 的导函数，则以下结论一定正确的是 ( )
A. fx+2
7
为奇函数 B. f
2
1
=f
2
1
C. f
2
3
=-f
2
D. f x 为偶函数
第II卷(非选择题)
三、填空题：本题共3小题，每小题5分，共15分．
1
12.小明上学要经过两个有红绿灯的路口，已知小明在第一个路口遇到红灯的概率为 ，若他在第一个路口
4
3
遇到红灯，第二个路口没有遇到红灯的概率为 ，在第一个路口没有遇到红灯，第二个路口遇到红灯的
4
1
概率为 ，则小明在第二个路口遇到红灯的概率为 ．
4
π
13.已知α,β∈0,
2
，若P=sinαsin2β+cosαcosβ，则P的最大值为 ．
14.已知抛物线C:x2=2py(p>0)的焦点为F，直线l与抛物线C相切于点P(异于坐标原点O)，与x轴交于
点Q，若PF =2,FQ
=1，则p= ；向量FP与PQ的夹角为 ．
四、解答题：本题共5小题，共77分。解答应写出文字说明、证明过程或演算步骤。
15.(13分)已知函数fx
1
=ax+ ．
ex
(1)讨论fx 的单调性；
(2)若直线y=1与曲线y=fx 相切，求a的值．
π
16.(15分)如图，在三棱台ABC-A B C 中，AB=AC=2A B =2AA =4 2，∠A AB=∠A AC= ，∠BAC
1 1 1 1 1 1 1 1 3
π
= ．
2
·107·(1)证明：A A⊥B C ；
1 1 1
(2)求直线BB 与平面A ACC 所成角的正弦值．
1 1 1
17.(15分)某数学兴趣小组模拟“刮刮乐”彩票游戏，每张彩票的刮奖区印有从10个数字1，2，3，⋯，10中
随机抽取的3个不同数字，刮开涂层即可兑奖，中奖规则为：若3个数的积为3的倍数且不为5的倍数
时，中三等奖；若3个数的积为5的倍数且不为3的倍数时，中二等奖；若3个数的积既为3的倍数，又为
4的倍数，且为7的倍数时，中一等奖；其他情况不中奖．
(1)随机抽取一张彩票，求这张彩票中奖的概率；
(2)假设每张彩票售价为aa∈N* 元，且三、二、一等奖的奖金分别为5元，10元，50元，从出售该彩票
可获利的角度考虑，求a的最小值．
x2 y2
18.(17分)已知椭圆C: + =1的右焦点为F,A为椭圆上一点，O为坐标原点，直线OA与椭圆交于另
4 3
一点B，直线AF与椭圆交于另一点D(点B、D不重合)．
3
(1)设直线AD,BD的斜率分别为k ,k ，证明：k ⋅k =- ；
AD BD AD BD 4
(2)点P为直线x=4上一点，记PA,PF,PD的斜率分别为k ,k ,k ，若k +2k +k =4，求点P的坐标．
1 2 3 1 2 3
19.(17分)在数列a n 中，若存在常数t，使得a n+1 =a 1 a 2 a 3 ⋯a n +tn∈N* 恒成立，则称数列a n 为“Ht 数
列”．
1
(1)若c n =1+ n ，试判断数列c n 是否为“Ht 数列”，请说明理由；
(2)若数列a n 为“Ht 数列”，且a 1 =2，数列b n
n
为等比数列，且a2 i =a n+1 +log 2 b n -t，求数列b n
i=1
的
通项公式；
(3)若正项数列a n 为“Ht 数列”，且a >1,t>0，证明：lna <a -1． 1 n n
·108·C. y=fx
π
的图像关于点 ,1
3
对称 D. y=fx
π
的图像关于直线x= 对称
6
10.已知点A4,1
x2 y2
,F,F 分别为双曲线C: - =1的左､右焦点，P为C的右支上一点，则 ( ) 1 2 2 7
A. PA +PF 1 <6 2 B. PA +PF 2 ≥3 2
C. PA -PF 1 ≤- 2 D. PA -PF 2 >- 2
11.在△ABC中，AB=AC=5,BC= 50，边AB,AC在平面α上的射影长分别为3，4，则边BC在α上的射影
长可能为 ( )
A.7 B.6 C.1 D.0
第II卷(非选择题)
三、填空题：本题共3小题，每小题5分，共15分．
12.已知向量a=k,2
,b=1,1
，若b⊥b-a
，则k= ，a+b = .
13.记S n 为等差数列a n 的前n项和，若a =3,S =25，则S = . 2 5 7
14.已知a>0且a≠1，函数 f x
2ax
= -x在0,+∞
ax-1
的最大值为-3，则 f x 在-∞,0 的最小值为
.
四、解答题：本题共5小题，共77分。解答应写出文字说明、证明过程或演算步骤。
15.(13分)
记△ABC的内角A,B,C的对边分别为a,b,c，已知2b=c.
(1)若cosB=sinC，求tan2B；
3
(2)若cosA= ,a= 2，求△ABC的面积.
4
16.(15分)
如图，在四棱锥P-ABCD中，底面ABCD是正方形，E,F分别为PB,PC的中点，G为线段AC上一点，且
CG=3AG.
(1)证明：EG∥平面BDF；
(2)若PD⊥平面ABCD，且AD=2PD，求二面角B-EG-D的正弦值.
17.(15分)
已知某客运轮渡最大载客质量为4000kg，且乘客的体重(单位：kg)服从正态分布N60,100 .
·110·(1)记X为任意两名乘客中体重超过70kg的人数，求X的分布列及数学期望(所有结果均精确到0.001)；
(2)设随机变量X ii=1,2,⋯,n 相互独立，且服从正态分布Nμ,σ2
n
X -nμ
i
，记ξ= i=1 ，则当n≥20时，
nσ
可认为ξ服从标准正态分布N0,1 .若保证该轮渡不超载的概率不低于97.7%，求最多可运载多少名乘
客.
附：若随机变量η服从正态分布Nμ,σ2 ，则P(μ-σ<η<μ+σ)=0.6826；若ξ服从标准正态分布
N0,1 ，则P(ξ<2)=0.977；0.15872≈0.0252，0.84132≈0.7078，0.1587×0.8413≈0.1335.
18.(17分)已知抛物线C:y2=4x的焦点为F,△PQR各顶点均在C上，且PF+QF+RF=0.
(1)证明：F是△PQR的重心；
(2)△PQR能否是等边三角形？并说明理由；
21
(3)若P,Q均在第一象限，且直线PQ的斜率为 ，求△PQR面积.
3
19.(17分)
已知函数fx
x-b
=2aea -lnx-1.
(1)若a=-log 2 e,b=0，求fx 的极值；
(2)若a,b∈0,1 ，设x 1 =1,x n+1 =fx n .证明：
(i)x <x ；
n n+1
4b-1
(ii)x -x <
n n+2
.
an-1
·111·
