文档内容
2023~2024 学年度下期高二期末联考
数学
考试时间 120分钟,满分 150分
注意事项:
1.答题前,考生务必在答题卡上将自己的姓名、座位号、准考证号用0.5毫米的黑色签字笔填
写清楚,考生考试条形码由监考老师粘贴在答题卡上的“贴条形码区”.
2.选择题使用2B 铅笔填涂在答题卡上对应题目标号的位置上,如需改动,用橡皮擦擦干净后
再填涂其它答案;非选择题用 0.5毫米的黑色签字笔在答题卡的对应区域内作答,超出答题区
域答题的答案无效;在草稿纸上、试卷上答题无效.
3.考试结束后由监考老师将答题卡收回.
一、选择题:本题共 8小题,每小题 5分,共 40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
1. 记 为等差数列 的前 项和,若 = 22,则 =
11 6
A.2 B .3 C.10 D.4
2. 若 +1 6 = 6 + 5 + 4 + 3 + 2 + 1 + ,则 + + + =
6 5 4 3 2 1 0 6 5 4 3 2 1 0
− − −
A.-1 B.1 C.64 D.0
3. 已知在四面体 中, = , = , = , = 1 , 为 的中点,若 =
3
+ + ,则 −+ + = ��� �� ��� �� ��� �� ��� �� ��� ��
3 1 1
A.3 B. C. D.
4 2 3
4. 若等比数列 的各项均为正数,且3 , 1 ,2 成等差数列,则 10+ 4
5 7 6
2 8+ 2
A.3 B.6 C.9 D.18
5. 若函数 f(x)ax2blnx(a 0,b0) 在点 1, 1 处的切线的斜率为1,则1 + 1 的最小值
为
1
A. B.2+3 2 C.3+2 2 D.3 2
2
6. 某市人民政府新招聘进 5 名应届大学毕业生,分配给教育、卫生、医疗、文旅四个部门,
每人只去一个部门,若教育部门必须安排 2 人,其余部门各安排 1 人,则不同的方案数为
A.52 B.60 C.72 D.360
{#{QQABYQAEogiIAJJAAQgCAwHQCkGQkAACCYgOQBAEsAAAgBNABCA=}#}7. 南宋数学家杨辉为我国古代数学研究作出了杰出贡献,他的著名研究成果 “杨辉三 角” 记
录于其重要著作《详解九章算法》中, 该著作中的 “垛积术” 问题介绍了高 阶等差数列. 以高
阶等差数列中的二阶等差数列为例,其特点是从数列中第二项开 始,每一项与前一项的差构
成等差数列. 若某个二阶等差数列 的前四项分别为:2,3,8,17 ,则下列说法错误的是
A. > 0 B. = 192
11
C. 数列 是单调递增数列 D. 数列 有最大项
2 2
8. 已知直线 = 与双曲线 : = 1 > > 0 分别相交于 , 两个不同的点, 是
2 2
3
双曲线上不同 于 , 的一点,设 直 线 − , 的斜率分别为 1 , 2 ,则当 e e 2.7
1 2 1
取得最小值时,双曲线 的离心率为
− ≈
7 5
A. B. 2 C. D.2
2 3
二、选择题:本题共 3小题,每小题 6分,共 18分.在每小题给出的四个选项中,有多项符合
题目要求;全部选对的得 6分,部分选对的得部分分,有选错的得 0分.
9. 等差数列 的前 项和为 , > 0, + = 0,则
1 2 14
A. = 0 B. <
8 +1
C. < D. 当 < 0 时, 的最小值为 16
7 9
10. 对于三次函数 = 3 + 2 + + 0 ,现给出定义: 设 ′ 是函数 的
≠
导数, ′′ 是 ′ 的导数,若方程 ′′ = 0 有实数解 ,则称点 , 为函 数
0 0 0
= 3 + 2 + + 0 的 “拐点”. 经过探究发现: 任何一个三次函数都 有 “拐点”,
任 何一 个 三次 函数 都 有 对 称 ≠ 中心,且 “拐点” 就是对称中心. 已知函数 = 1 3 + 1 2 ,则
3 2
A. 函数 有三个零点
B. 函数 有两个极值点
C. 点 1 , 1 是曲线 = 的对称中心
2 12
−
D. 方程 1 = 0 有三个不同的实数根
10
−
11. 已知数列 的通项公式为 = 98 ,前 项积为 ,则下列说法正确的是
99
−
−
A. 在数列 中, 是最大项 B. 在数列 中, 是最小项
10 9
{#{QQABYQAEogiIAJJAAQgCAwHQCkGQkAACCYgOQBAEsAAAgBNABCA=}#}C. 数列 单调递减 D. 使 取得最小值的 为 9
三、填空 题 :本题共 3小题,每小题 5分,共15分.
6
12. 在 + 1 的展开式中,常数项为_________
+1, 为奇数 ,
13. 已知数列 满足 = 1, = 2, = ,若 为数列 的前 项
1 2 +2
2 ; 为偶数
和,则 10 =_________
14. 已知 关于 的不等式 2 < e (其中 < 1). 的解集中恰有两个整数,则
实数 的取值范围是_________ −
− ∈
四、 解答题:本题共 5小题,共 77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)
已知等差数列 的公差为 0 ,前 项和为 ,且满足 = 2 +19; , ,
5 4 1 2
成等比数列.
7 ≠
(1)求数列 的通项公式;
(2)设 = 1 ,数列 的前 项和为 ,求 .
+1
16.(15分)
某家会员足够多的知名水果店根据人的年龄段办理会员卡, “年龄在 20 岁到34岁之间
的会员” 为 1 号会员,占比 20%,“年龄在 35 岁到 59 岁之间的会员” 为 2 号会员,占比
50%,“年龄在 60 岁到 80 岁之间的会员” 为 3 号会员,占比 30% ,现对会员进行水果质
量满意度调查. 根据调查结果得知,1 号会员对水果质量满意的概率为 1,2 号会员对水果质
2
量满意的概率为 3,3 号会员对水果质量满意的概率为 2 .
5 3
(1)随机选取 1 名会员, 求其对水果质量满意的概率;
(2)从会员中随机抽取 2 人,记抽取的 2 人中,对水果质量满意的人数为 ,求 的
分布列和数学期望.
{#{QQABYQAEogiIAJJAAQgCAwHQCkGQkAACCYgOQBAEsAAAgBNABCA=}#}17.(15分)
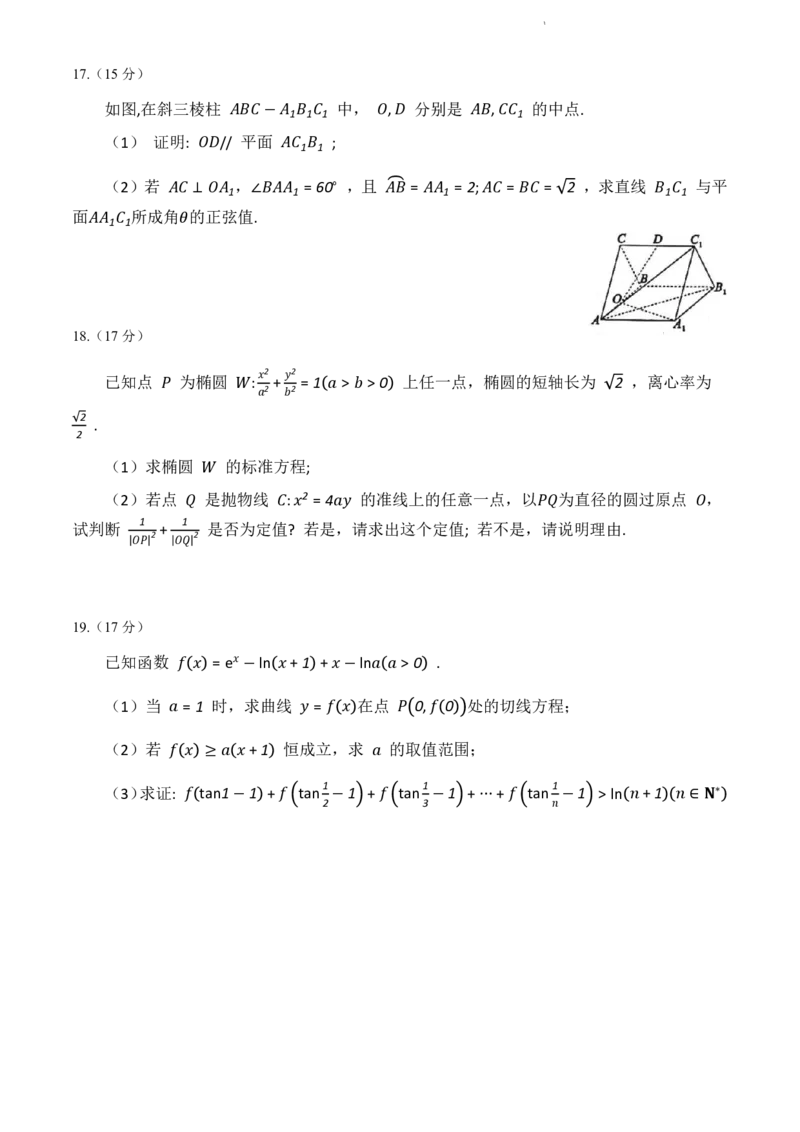
如图,在斜三棱柱 中, , 分别是 , 的中点.
1 1 1 1
(1) 证明: // 平 面 − ;
1 1
(2)若 , = 60 ,且 = = 2; = = 2 ,求直线 与平
1 1 1 1 1
∘
面 1 1 所成角 的 ⊥ 正 弦值 ∠ . �
18.(17分)
2 2
已知点 为椭圆 : + = 1 > > 0 上任一点,椭圆的短轴长为 2 ,离心率为
2 2
2
.
2
(1)求椭圆 的标准方程;
(2)若点 是抛物线 : 2 = 4 的准线上的任意一点,以 为直径的圆过原点 ,
试判断 1 + 1 是否为定值? 若是,请求出这个定值; 若不是,请说明理由.
2 2
19.(17分)
已知函数 = e ln +1 + ln > 0 .
− −
(1)当 = 1 时,求曲线 = 在点 0, 0 处的切线方程;
(2)若 +1 恒成立,求 的取值范围;
(3)求证 : t ≥ an 1 1 + tan 1 1 + tan 1 1 + + tan 1 1 > ln +1
2 3
∗
− − − ⋯ − ∈
{#{QQABYQAEogiIAJJAAQgCAwHQCkGQkAACCYgOQBAEsAAAgBNABCA=}#}