广西壮族自治区“贵百河”联考2024-2025学年高二下学期3月月考数学试卷（含答案）_2024-2025高二（7-7月题库）_2025年04月试卷(1)

2023 级“贵百河”3 月高二年级新高考月考测试 数 学 （考试时间：120分钟 满分：150分） 注意事项： 1．答题前，考生务必将自己的姓名、准考证号填写在答题卡上。 2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑；如需改 动，用橡皮擦干净后，再选涂其他答案标号。 3．回答非选择题时，将答案写在答题卡上，写在试卷上无效。 一、单选题：本题共8小题，每小题5分，共40分． 在每小题给出的四个选项中，只有一项是符 合题目要求的． 1．设集合A  xR∣x23x0  ,B2,2，则C AB（ ） R A． B．2 C．2 D．2,2 i 2．若复数z （i为虚数单位），则z在复平面内对应的点位于（ ） 12i A．第一象限 B．第二象限 C．第三象限 D．第四象限 3．在电影《哪吒之魔童闹海》中，哪吒、敖丙、太乙真人、申公豹、鹿童五人参加一场仙法比试， 需要站成一排拍照留念。哪吒和敖丙要求必须相邻，且太乙真人不能站在两端，那么共有多少 种不同的站法（ ） A．18 B．12 C．28 D．24 x 4．曲线y  cosx在点（0，1）处的切线方程为（ ） 2 A．x2y20 B．x y10 C．x2y20 D．2x y20 y 5．如果实数x、y满足x2 y26x40，那么 的最大值是（ ） x 2 + 5 2 5 1 A． B． C． 5 D． 5 5 2 6．“总把新桃换旧符”（王安石）、“灯前小草写桃符”（陆游），春节是中华民族的传统节日， 在宋代人们用写“桃符”的方式来祈福避祸，而现代人们通过贴“福”字、贴春联、挂灯笼等 方式来表达对新年的美好祝愿。某商家在春节前开展商品促销活动，顾客凡购物金额满68元， 则可以从“福”字、春联和灯笼这三类礼品中任意免费领取一件，若有3名顾客都领取一件礼 品，则他们三人领取的礼品种类都不相同的概率是（ ） 1 1 2 1 A． B． C． D． 9 27 9 3 高二数学 第 1 页 共 4 页 {#{QQABRYKUogigAAIAAQgCUwHyCgMQkBACAaoGBAAQIAAAgANABAA=}#}x2 y2 7．已知双曲线C:  （1 a 0，b0）的左、右焦点分别为 F ，F ，P 为 C 的右支上一点， 1 2 a2 b2 ∠ PFF 45，∠ FPF 60则C的离心率为（ ） 1 2 1 2 3 2 6 3 2 6 A． B． C． 3 D． 31 2 2 1 11 ln3 8．设a  ，b ，ce10，则a，b，c 的大小关系为（ ） 10 3 A．cab B．cba C．a b  c D．b  a  c 二、多选题：本题共3小题，每小题6分，共18分，在每小题给出的四个选项中，有多项符合题 目要求．全部选对的得6分，部分选对的得部分分，有选错的得0分． 9．已知等差数列a 的前 项和为S ，a 12，公差d 2，则下列说法正确的是（ ） n n 1 A．a 是递增数列 B．1是数列a 中的项 n n S  C．数列S 中的最小项为S D．数列 n是等差数列 n 8  n  π 10．对于函数 f(x)sin2x和g(x)sin(2x )，下列说法中正确的有（ ） 4 A． f(x)与g(x)有相同的最小值 B． f(x)与g(x)的图象有相同的对称中心 C． f(x)与g(x)有相同的最小正周期 D．当x0，2时， f(x)与g(x)的图像有4个交点 y2 11．已知双曲线C:x2  （1 b0）的左、右焦点分别为F ，F ，其一条渐近线方程为y  3x，点 1 2 b2 A为C 的左支上任意一点，则下列说法正确的是（ ） A．b 3 B．F 到渐近线y  3x的距离是 3 2 C．若B（0，2），则 AB  AF 的最小值为 4 2 2 6 D．若点P（-3，t）为C 的左支上一点，则△PF F 的内切圆的半径为 1 2 2 三、填空题：本题共3小题，每小题5分，共15分．       12．如果 a 1， b  2 ，ab 1，则 ab 的值是_______． 2 13．在二项式（ x )n（nN)的展开式中，只有第五项的二项式系数最大，则展开式中x的系数 x 为_______．（用数字作答) 14．若函数 f(x) xlnxax2在区间（0，）上有两个极值点，则实数a的取值范围是___________． 高二数学 第 2 页 共 4 页 {#{QQABRYKUogigAAIAAQgCUwHyCgMQkBACAaoGBAAQIAAAgANABAA=}#}四、解答题：本题共5小题，共77分． 解答应写出文字说明，证明过程或演算步骤． 6 15．（13分）△ABC的内角A，B，C的对边分别为a，b，c，已知a2 b2 c2  2ab0，sinC  sinB， 3 B为锐角． （1）求B； （2）若c 4 2，求△ABC 的周长． 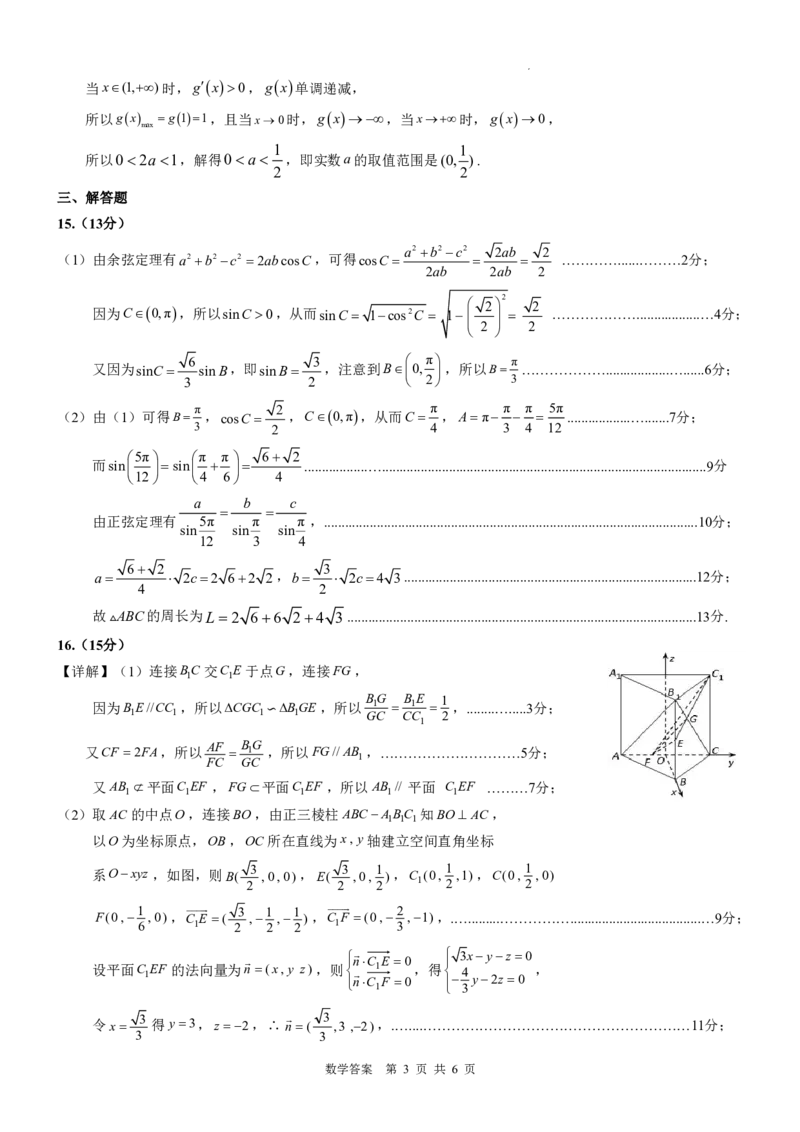16．（15分）如图，正三棱柱ABCABC 中，E是棱BB 的中点，AB  AA 1，点F在AC 上， 1 1 1 1 1 且CF 2FA ． （1）求证：AB //平面C EF； 1 1 （2）求点C 到平面C EF 的距离． 1 17．（15分）已知aR，函数 f(x)ax2lnx． （1）求函数 f(x)的单调区间； （2）当a=1 时，若对任意x（0，）， f(x)bx3恒成立，求实数b的最大值． 高二数学 第 3 页 共 4 页 {#{QQABRYKUogigAAIAAQgCUwHyCgMQkBACAaoGBAAQIAAAgANABAA=}#}18．（17分）在平面直角坐标系xOy 内，已知曲线C 上任意一点到点F（2，0）的距离比到直线x 3 的距离少1． （1）求曲线C 的方程； （2）点A（2，t）（t>0）在曲线C 上，若直线l 斜率存在并与抛物线C 交于M、N 两点（M、 N异于点A）．若AM  AN ，证明：直线l 过定点． 19．（17分）定义：若无穷数列a 满足a a 是公比为q的等比数列，则称数列a 为“Mq n n1 n n 数列”.设数列b 中b 1, b 5． n 1 3 （1）若b 3, 且数列b 是“Mq数列”，求数列b 的通项公式； 2 n n （2）设数列b 的前n项和为S ，且S 4S n，请判断数列b 是否为“Mq数列”， n n n1 n n 并说明理由； 6058 b 1 6059 （3）若数列b 是“M3数列”，是否存在正整数m，n，使  m  ，若存在，请 n 2019 b 1 2019 n 求出所有满足条件的正整数m，n；若不存在，请说明理由． 高二数学 第 4 页 共 4 页 {#{QQABRYKUogigAAIAAQgCUwHyCgMQkBACAaoGBAAQIAAAgANABAA=}#}2023 级“贵百河”3 月高二年级新高考月考测试 数 学 参考答案 一、选择题 题号 1 2 3 4 5 6 7 8 9 10 11 答案 C B D A D C B A AD ACD ABD 1.C【详解】集合A  xR∣x23x0  ，则C A  xR x230    x 0 x 3  R   则C AB  2 .故选：C. R i i i12i 2i 2 1 2.B【详解】因为z      i， 12i 12i 12i12i 5 5 5  2 1 故复数z在复平面内对应的点的坐标为 , ，位于第二象限.故选：B.  5 5 3.D【解析】把哪吒和敖丙看作一个整体，与申公豹、鹿童全排列，有A 3 12种排法；同时哪吒和敖丙两人之 3 间也有2种排法；这样就形成了4个空，因为太乙真人不能站在两端，所以太乙真人只能插入中间的1个空，有2 种插空方法。根据分步乘法计数原理，不同的站法共有12×2×2=24种.故选D. 1 1 1 4.A【详解】 y  sinx当x0时其值为 ，故所求的切线方程为，y1 x， 2 2 2 即x2y20，故选：A. 5．D【详解】x2 y26x40，即x32  y2 5，圆心为3,0，半径为 5 ， y 的几何意义是圆上一点x,y与2,0 连线的斜率， 结合图像易知，当过（-2,0）的直线与圆相切时，斜 x 2 + y 1 率最大，即 最大是 .故选：D. x 2 2 + 6．C【详解】根据题意，3名顾客都领取一件礼品，基本事件总数共有：33327种， 他们三人领取的礼品种类都不相同的基本事件有A3 6种，故根据古典概型公式得他们三人领取的礼品种类都 3 A3 2 不相同的概率是P 3  . 故选：C 27 9 7.B【详解】依题意得， PF F 75 ∠ 2 1= c 2c FF sin60 3 2  6 则C的离心率为   1 2   .故选：B. a 2a PF - PF sin75-sin45 2 1 2 8.A【解析】根据题意，a 11 1,b ln3 1，e1 1 0 1，则ab,cb，构造函数 f xexx1(x0)，所以 10 3  1  1 1 fxex10恒成立，所以 f xexx1在0,上单调递增，所以 f  e10  1 f 00，即 10 10 1 11 e10  ，所以ca，故cab.故选：A 10 数学答案 第 1 页 共 6 页 {#{QQABRYKUogigAAIAAQgCUwHyCgMQkBACAaoGBAAQIAAAgANABAA=}#}9.AD 【详解】解：对于 ，由已知 ，故数列为递增数列，故A正确． 对于 ，由题意数列为以 为首项 ， =22 为 > 公 0 差的等差数列， ，解得 不是正整数，故 15 B错误 ．对于 ， 且−12 是递增数列，故数列 中的∵最1小=项−为12+2( ，−故1)C错误． = 2 对于 ， 7 =0, { } ，故数列 是等{差 数} 列，D正确． 故6选=A 7 D. 2 ( −1) −12 + 2 10.ACD 【详 解 = 】显然 f(x) =  − g( 1 x 3 ) 1， { A 选 } 项正确；对于B选项，f(x)的对称中心为( kπ ,0),kZ，g(x)的 min min 2 kπ  2π 对称中心为(  ,0),kZ，B选项错误；对于C选项，两者 f(x),g(x)的周期均为 π，C选项正确；对 2 8 2 于D选项，作出两者图像，观察发现有4个交点；故选：ACD. y2 b 11.ABD【详解】由x2 1b0，得a1，由其一条渐近线方程为y 3x， 3得b 3，A正确；双 b2 a= 曲线C的方程为x2 y2 1，F 2,0，点到直线的距离公式d |-2 3| 3，B正确；根据双曲线定义可得 3 1 = 2 = AF  AF 2a2，得 AF 2 AF ，又B0,2，F 2,0， 2 1 2 1 1 因此 AB  AF  AB  AF 2 BF 22 22， 2 1 1 当A是线段BF与C的交点时，满足题意，此时 AB  AF 的最小值为2 22，C错误; 1 2 由点P3,t为C的左支上一点，得P  3,2 6  .由F 2,0，得 PF 5， PF 2 PF 7， 1 1 2 1 又 FF 2c4，因此PFF 的周长为l  FF  PF  PF 16， 1 2 1 2 1 2 1 2 1 知PFF 的面积为S  FF 2 6 4 6.设PFF 的内切圆半径为r， 1 2 PF1F2 2 1 2 1 2 1 6 则S  lr 4 6，解得r ，D正确.故选：ABD. PF1F2 2 2 三、填空题 12.【答案】1 【详解】因为 a  1， b   2，a  b  1， 所以 a  b    a  b  2  a  2 b  2  2a  b   12  2 2  21 1 ， 13.【答案】112 【详解】因为只有第五项的二项式系数最大，所以n8， 故( x 2 )n（nN ）的展开式通项为T Cr  x 8r   2  r 2r Crx 4 3 2 r ，令4 3 r 1，解得r2， x r1 8  x 8 2 所以展开式中x的系数为.(2)2C2 112 故答案为：112 8 14.【答案】(0, 1 ) 【详解】由函数 f  x  xlnxax2，可得， f(x)lnx12ax 2 因为函数 f x在区间(0,)上有两个极值点，即 f x0在(0,)上有两个不等的实数根， lnx1 lnx1 即2a  在(0,)上有两个不等的实数根，即函数gx 和y 2a的图象有两个交点， x x lnx1 lnx 又由gx ，可得gx ，当x(0,1)时，gx0，gx单调递增； x x2 数学答案 第 2 页 共 6 页 {#{QQABRYKUogigAAIAAQgCUwHyCgMQkBACAaoGBAAQIAAAgANABAA=}#}当x(1,)时，gx0，gx单调递减， 所以gx g11，且当x0时，gx，当x时，gx0， max 1 1 所以02a1，解得0a ，即实数a的取值范围是(0, ). 2 2 三、解答题 15.（13分） a2b2c2 2ab 2 （1）由余弦定理有a2b2c2 2abcosC，可得cosC    …………......………2分； 2ab 2ab 2 2 因为C0,π，所以sinC0，从而sinC  1cos2C  1   2   2 ………………..................…4分；    2  2 6 3  π π 又因为sinC sinB，即sinB ，注意到B0, ，所以B ………………..................…......6分； 3 2  2 3 （2）由（1）可得B π ，cosC  2 ，C0,π，从而C  π ，Aπ π  π  5π ..................….......7分； 3 2 4 3 4 12 5π π π  6 2 而sin sin   ..................…............................................................................................9分 12 4 6 4 a b c   由正弦定理有 5π π π ，..........................................................................................................10分； sin sin sin 12 3 4 6 2 3 a  2c2 62 2，b  2c4 3...................................................................................12分； 4 2 故ABC的周长为L2 66 24 3 ...................................................................................................13分. 16.（15分） 【详解】（1）连接BC交C E于点G，连接FG， 1 1 BG BE 1 因为BE//CC ，所以CGC BGE，所以 1  1  ，........….....3分； 1 1 1 1 GC CC 2 1 ∽ 又CF 2FA，所以 AF  B 1 G ，所以FG//AB ，…………………………5分； 1 FC GC 又AB 平面C EF ，FG平面C EF ，所以AB // 平面 C EF ………7分； 1 1 1 1 1 （2）取AC的中点O，连接BO，由正三棱柱ABCABC 知BO AC， 1 1 1 以O为坐标原点，OB，OC所在直线为x, y轴建立空间直角坐标 系Oxyz ，如图，则B( 3 ,0,0)，E( 3 ,0, 1 )，C (0, 1 ,1)，C(0, 1 ,0) 2 2 2 1 2 2 F(0, 1 ,0)，C  E  ( 3 , 1 , 1 ) ，C  F  (0, 2 ,1)，.….........…………….....................................…9分； 6 1 2 2 2 1 3   n  C E 0   3xyz0 设平面C 1 EF 的法向量为n(x,y z)，则   n  C 1 1 F 0 ，得    4 3 y2z0 ， 令x 3 得y3，z2， n  ( 3 ,3 ,2)，.…....…………………………………………………11分； 3 3 数学答案 第 3 页 共 6 页 {#{QQABRYKUogigAAIAAQgCUwHyCgMQkBACAaoGBAAQIAAAgANABAA=}#} （2）取向量CC (0,0,1) ， …..........……....................……...................…………………….....…12分； 1   nCC 2 30 1 则 d  n   40 10 ….....…….....……........….....……........…....................………….…14分； 3 所以点C 到平面C EF 的距离为 30 …………….....……....................………………………...……...15分； 1 10 17.（15分） 【详解】(1) f x的定义域为(0,)， .…................................................................................................1分； 1 ax1 fxa  ， ................................................................................................................................2分； x x 当a0时， fx0， f x在(0,)上单调递减.....................................................................................3分； 1 1 当a0时，令 fx0x ；令 fx00x ......................................................................5分； a a 综上，当a0时， f x的减区间为(0,)，无增区间；  1 1  当a0时， f x减区间为0, ，增区间为  , ...........................................................................6分；  a a  (2)∵a1，∴ f  x  x2lnx， f  x bx3恒成立 1 lnx 即b1  (x0)恒成立，................................................................................................................8分； x x 1 lnx lnx2 令gx1  ，则gx ，....................................................................................................9分； x x x2 由gx0，得xe2；由gx0，得0xe2， 故gx在  0,e2 上单调递减，在(e2,)上单调递增， .............................................................................12分； ∴gx  g  e2 1 1 ，即b1 1 ，.......................................................................................................14分； min e2 e2 1 故实数b的最大值是1 .............................................................................................................................15分； e2 18.（17分） 【详解】（1）因为曲线C上任意一点到点F(2,0)的距离比到直线x3的距离少1， 所以曲线C上任意一点到点F(2,0)的距离跟到直线x2的距离相等，.................................................1分； 又点F(2,0)不在直线x2上，根据抛物线的定义可知，曲线C是以F(2,0)为焦点， x2为准线的抛物线， .......................................................................................................................2分； 所以曲线C的方程为：y2 8x ................................................................................................................4分； 数学答案 第 4 页 共 6 页 {#{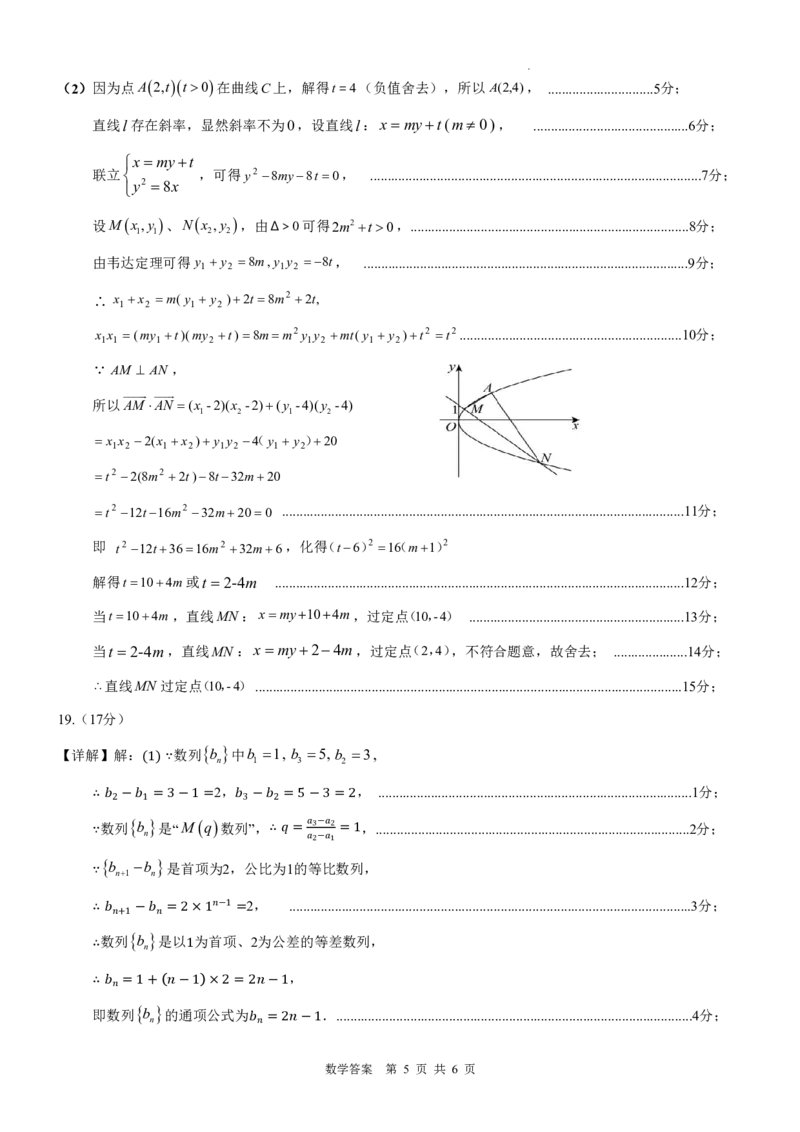QQABRYKUogigAAIAAQgCUwHyCgMQkBACAaoGBAAQIAAAgANABAA=}#}（2）因为点A2,tt0在曲线C上，解得t 4（负值舍去），所以A(2,4)， ..............................5分； = 直线l存在斜率，显然斜率不为0，设直线l：xmyt(m 0)， ............................................6分； xmyt 联立 ，可得y2 8my8t 0， ..............................................................................................7分； y2 8x 设Mx,y 、Nx ,y ，由 0可得2m2t0，...............................................................................8分； 1 1 2 2 Δ> 由韦达定理可得y y 8m,y y 8t， ............................................................................................9分； 1 2 1 2  x x m(y y )2t 8m2 2t, 1 2 1 2 x x (my t)(my t)8mm2y y mt(y y )t2 t2...............................................................10分； 1 1 1 2 1 2 1 2  AM  AN ，   所以AM AN (x -2)(x -2)(y -4)(y -4) 1 2 1 2  x x 2(x x ) y y （4 y  y ）20 1 2 1 2 1 2 1 2 t2 2(8m2 2t)8t32m20 t2 12t16m2 32m200 ..................................................................................................................11分； 即 t2 12t3616m2 32m6，化得（t6）2 1（6 m1）2 解得t 104m或t 2-4m ....................................................................................................................12分； 当t 104m，直线MN ：xmy104m，过定点（10，-4） .............................................................13分； 当t 2-4m，直线MN：xmy24m，过定点（2，4），不符合题意，故舍去； .....................14分； 直线MN过定点（10，-4）.........................................................................................................................15分； ∴ 19.（17分） 【详解】解： 数列 b  中b 1, b 5, b 3, n 1 3 2 (1)∵ 2， ， .........................................................................................1分； ∴数 2 列− b 1=是3 “ − M 1= q数列 3 ” −， 2 =5−3=2 ，.........................................................................................2分； n 3− 2 ∵b b  是首项为2，公比 ∴ 为 1 = 的 等 2− 比 1 数 = 列 1 ， n1 n ∵ 2， ..................................................................................................................3分； −1 ∴数 列 +1−b  是=以2×为1首项=、2为公差的等差数列， n ∴ 1 ， ∴即 数 列=1b+ 的 通−1项公×式2=为2 −1 ．.....................................................................................................4分； n =2 −1 数学答案 第 5 页 共 6 页 {#{QQABRYKUogigAAIAAQgCUwHyCgMQkBACAaoGBAAQIAAAgANABAA=}#}数列 b  不是“Mq数列”，理由如下： n (2) S 4S n n1 n ∵ 当 时，S 4S① (n1) .....................................................................................................5分； n n1 ≥2 得：b 4b 1 ， ... ② .........................................................................................................6分； n1 n ①b −② 4b 1 ， ③ n2 n1 得 ④ ， ，..........................................................................................7分； ④由 −③ +2 ，− +1 =可4得 +1− ， ...... ... ≥ .... 2 ................................................................................................8分； 3 3 =4 2−1 3 =5 2 =2 ， ， ， .................................................................9分； 3 1 7 ∴ 则 2− 1 =2−1= 2 3− 对 2 = 任 2 意 ∴ 为 3 正 − 整 数 2 = 不 7 恒 成 2 立 − ， 1 即数列 b  不是“Mq数列”． .............10分； n 由数 列 +2 − b  是 +1 “ = M 4 3  + 数 1 列 − ” ， 可得 b b  是公比为3的等比数列， n n1 n (3)则 ， 由 ， ，可得 ， ...................................................................11分； 3− 2 =3 2− 1 1 =1， ， 3 =5 2 =2 −1 −1 ∴ +1− =3 2− 1 =3 ∴ − 1 = 2− 1 + 3− 2 +⋯+ − −1 2 −2 =1+3+3 ++3 −1 1× 1−3 = 1−3 ， ..........................................................................................................................................12分； 1 −1 =2 3 −1 则 ， ...................................................................................................................................13分； 1 −1 若正 整 = 数 2 3 、 满 +1 足 6059 ，则 6059， 6058 −1 6058 3 −1 −1 由3 2019 < − ， 1 < 则 2 3 019 2019 < 3 −1 −1，<即2019 ，......................................................14分； −1 −1 −1 −1 若 −1> ， 0 则 ,3 −1>3 0 −1> 3 ， −1 > −1 3 +1 3 3 −1 −1 8 −1 −1 −1 ≥ +2 3 −1 ≥ −1=9+ −1>9 不满足 6059， .................................................................................................................15分； −1 6058 3 −1 −1 若 2019< ， 3 则 −1 <2019 6059， 6058 3 −1 −1 = +1 2019<3 −1<2019 则 ， 6058 2 6059 −1 2019−3<3 −1<2019−3 即 ， 1 2 2 −1 则2 2 0 0 1 2 9 0 <3 −1<2019 ，解得正整数 ， ， .......................................................................16分； −1 因此，存<在3满足<条4件03的9 ， ， ，=8 ∴． ...=....9................................................................................17分； =9 =8 数学答案 第 6 页 共 6 页 {#{QQABRYKUogigAAIAAQgCUwHyCgMQkBACAaoGBAAQIAAAgANABAA=}#}