数学-江西省赣州市2023-2024学年高二第二（下）学期7月期末_2024-2025高二（7-7月题库）_2024年08月试卷_0813江西省赣州市2023-2024学年高二第二（下）学期7月期末

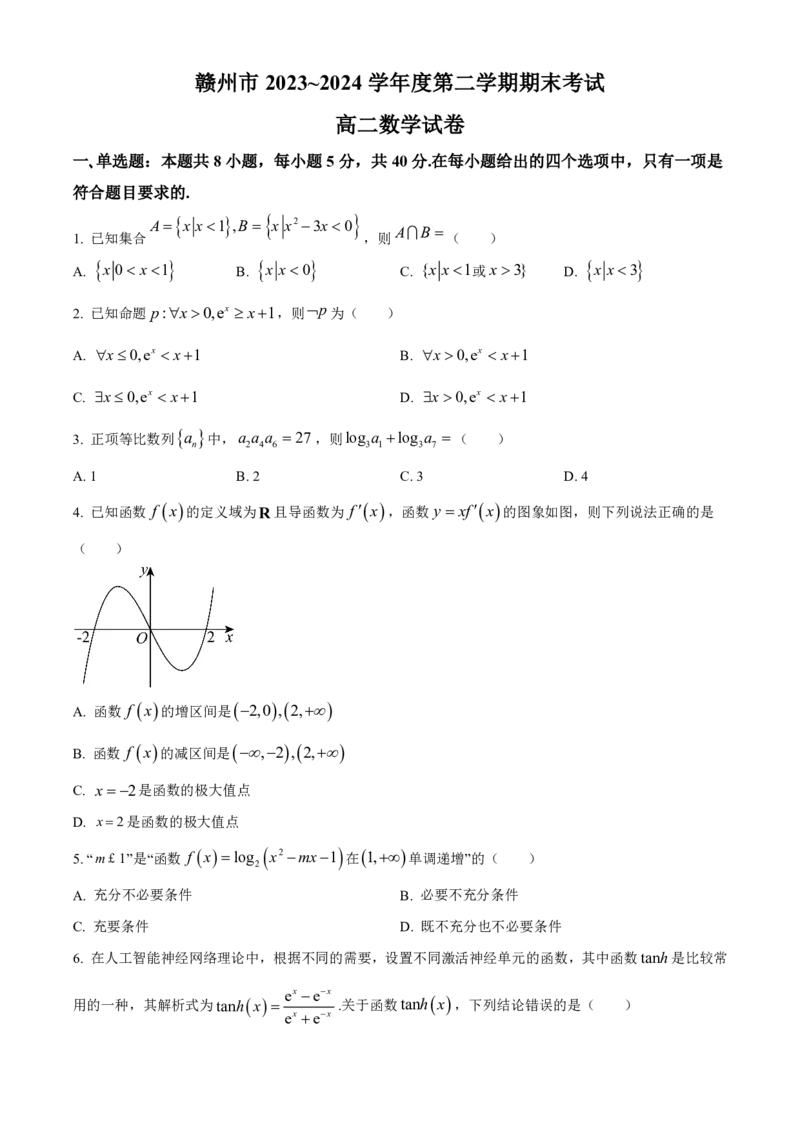
赣州市 2023~2024 学年度第二学期期末考试 高二数学试卷 一､单选题：本题共 8小题，每小题 5分，共 40分.在每小题给出的四个选项中，只有一项是 符合题目要求的. A  x x1  ,B   x x23x0  1. 已知集合 ，则 AB  （ ）       A. x 0 x1 B. x x0 C. {x x1或x3} D. x x3 2. 已知命题 p:x0,ex  x1，则p为（ ） A. x0,ex  x1 B. x0,ex  x1 C. x0,ex  x1 D. x0,ex  x1 3. 正项等比数列  a  中，a a a 27，则log a log a （ ） n 2 4 6 3 1 3 7 A.1 B.2 C.3 D.4 4. 已知函数 f  x  的定义域为R且导函数为 f x  ，函数y xf x  的图象如图，则下列说法正确的是 （ ） A. 函数 f  x  的增区间是 2,0  ,  2, B. 函数 f  x  的减区间是 ,2  ,  2, C. x2是函数的极大值点 D. x2是函数的极大值点 5.“m£1”是“函数 f  x log  x2mx1  在  1, 单调递增”的（ ） 2 A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件 6. 在人工智能神经网络理论中，根据不同的需要，设置不同激活神经单元的函数，其中函数tanh是比较常 用的一种，其解析式为tanh  x  ex ex .关于函数tanh  x  ，下列结论错误的是（ ） ex exA. tanh  x 1有解 B. tanh  x  是奇函数     C. tanh x 不是周期函数 D. tanh x 是单调递增函数 7. 已如A是函数 f  x  x2lnx图像上的动点，B是直线x y20上的动点，则A,B两点间距离 AB 的最小值为（ ） A 4 2 B.4 C. 2 2 D. 5 . a 8. 设等差数列  a  的前n项和为S ，公差为d 0, 10 1，则下列结论正确的是（ ） n n a 11 A. a a a  0 B. 使得S 0成立的最小自然数n是20 4 5 18 n S S S S C. 9  10 D. 21  22 9 10 a a 21 22 二､多选题：本题共 3小题，每小题 6分，共 18分.在每小题给出选项中，有多项符合题目要 求.全部选对的得 6分，部分选对的得部分分，有选错项得 0分. 9. 已知a,bR，且ab，a,b,c都不为0，则下列不等式一定成立的是（ ） 1 1 A.  B. ac bc a b a b 1 a 1 b C.  D.      c2 c2 2 2 10. 已知正数a,b满足4abab5，则下列结论正确的是（ ） A. ab的最大值为1 B. 4ab的最小值为4 1 1 10 C. 16a2 b2的最小值为9 D.  的最小值为 a1 b 9 11. 记方程xex 1的实数解为Ω（Ω是无理数），Ω被称为在指数函数中的“黄金比例”.下列有关Ω的结论 正确的是（ ） A. lnΩΩ0 1 1 B. Ω  ,  3 2 C. Ω2 2Ω10 1lnx D. 函数 f  x ex  的最小值为 f  Ω  x 三､填空题：本题共 3小题，每小题 5分，共 15分.f  x 1,x0 12. 已知函数 y f  x  是R上的奇函数，g  x  ，则g  g  0  __________. 3x 1,x0 1 nπ 13. 数列  a  的前n项和为S ，若a  sin ，则S __________. n n n n  n1  2 2024 14. 已知定义在R上的函数 f  x  满足 f  x1  f  x2  ，当x 0,3  时， f  x  x2 3x1 ，则 ex y f  x  在 1012,1012  上的零点个数为__________个. 四､解答题：本题共 5小题，共 77分.解答应写出文字说明､证明过程或演算步骤. 15. 已知函数 f  x ax3bx2 xR  的图象过点P 1,2  ，且在点P处的切线恰好与直线 3x y40平行.   （1）求函数 f x 的解析式； （2）求 f  x  在 4,1  上的最大值和最小值. 16. 已知等差数列  a  的公差d 0,a 5,a ,a ,a 成等比数列，数列  b  的前n项和公式为 n 4 1 3 7 n S 2b 2  nN* . n n     （1）求数列 a 和 b 的通项公式： n n （2）设c a b ，求数列  c  的前n项和T . n n n n n 17. 已知函数 f  x  为二次函数，有 f 1 0, f  4 5，__________，从下列条件中选取一个，补全到 1  3  题目中，① f  x  f  x ，②函数 f  x1  为偶函数，③ f  2 3 2  2    （1）求函数 f x 的解析式； （2）若g  x log  x23  log  x1  ，若对任意的x  1,2  ，总存在x 1,2  ，使得 2 2 1 2 g  x  f  x mx 成立，求实数m的取值范围. 2 1 1 18. 已知函数 f  x  xlnxax2, f  x  为 f  x 的导函数，记g  x  f x  ，其中a为常数.   （1）讨论g x 的单调性； （2）若函数 f  x  有两个极值点x ,x  x  x  ， 1 2 1 2①求a的取值范围； 1 ②求证：x x  . 1 2 a 19. 若在数列的每相邻两项之间插入此两项的和，形成新的数列，再把所得数列按照同样的方法不断构造出 新的数列.现对数列1，3进行构造，第一次得到数列1，4，3：第二次得到数列1,5,4,7,3：依次构造，第 n  nN* 次得到的数列的所有项之和记为a ，如a 1438. n 1 （1）求a ； 3   （2）求 a 的通项公式； n 1 1 1 1 5 （3）证明：     . a a a a 24 1 2 3 n赣州市 2023~2024 学年度第二学期期末考试 高二数学试卷 一､单选题：本题共 8小题，每小题 5分，共 40分.在每小题给出的四个选项中，只有一项是 符合题目要求的. A  x x1  ,B   x x23x0  1. 已知集合 ，则 AB  （ ）       A. x 0 x1 B. x x0 C. {x x1或x3} D. x x3 【答案】A 【解析】 【分析】先解一元二次不等式，求解集合B，再求交集即可. 【详解】因为B   x x23x 0    x x  x3  0    x 0 x3  ，又A  x x1  ,   所以AB  x 0 x1 . 故选：A. 2. 已知命题 p:x0,ex  x1，则p为（ ） A. x0,ex  x1 B. x0,ex  x1 C. x0,ex  x1 D. x0,ex  x1 【答案】D 【解析】 【分析】全称量词命题的否定，首先把全称量词改成存在量词，然后把后面结论改否定即可. 【详解】因为命题 p:x0,ex  x1是全称量词命题，则命题p为存在量词命题， 由全称量词命题的否定得，命题p：x0,ex  x1. 故选：D. 3. 正项等比数列  a  中，a a a 27，则log a log a （ ） n 2 4 6 3 1 3 7 A.1 B.2 C.3 D.4 【答案】B 【解析】 【分析】根据等比数列的性质求出a 即可得解. 4【详解】由等比数列性质可知a a a a3 27，解得a 3， 2 4 6 4 4 所以log a log a log aa log a2 2log 32， 3 1 3 7 3 1 7 3 4 3 故选：B 4. 已知函数 f  x  的定义域为R且导函数为 f x  ，函数y xf x  的图象如图，则下列说法正确的是 （ ） A. 函数 f  x  的增区间是 2,0  ,  2, B. 函数 f  x  的减区间是 ,2  ,  2, C. x2是函数的极大值点 D. x2是函数的极大值点 【答案】C 【解析】 【分析】根据函数图象确定导函数的符号，确定函数的单调区间和极值. 【详解】根据 y  xf x  的图象可知： 当x<2时， f ¢( x )>0；2 x0时， fx0，当0 x2时， fx0，当x2时， f ¢( x )>0. 所以 f  x  在 ,2  ,  2, 上单调递增，在 2,2  上单调递减. 因此函数 f  x  在x2时取得极小值，在x2取得极大值. 故ABD错误，C正确. 故选：C 5.“m£1”是“函数 f  x log  x2mx1  在  1, 单调递增”的（ ） 2 A 充分不必要条件 B. 必要不充分条件 . C. 充要条件 D. 既不充分也不必要条件 【答案】B 【解析】【分析】利用对数函数与复合函数的单调性计算即可. 【详解】由二次函数、对数函数的单调性及复合函数的单调性可知： 要满足函数 f  x log  x2mx1  在  1, 单调递增， 2 m  1 需要2 m0，  12 m110 因为01，所以“m£1”是“函数 f  x log  x2mx1  在  1, 单调递增”的必要不充分条件． 2 故选：B． 6. 在人工智能神经网络理论中，根据不同的需要，设置不同激活神经单元的函数，其中函数tanh是比较常 用的一种，其解析式为tanh  x  ex ex .关于函数tanh  x  ，下列结论错误的是（ ） ex ex A. tanh  x 1有解 B. tanh  x  是奇函数     C. tanh x 不是周期函数 D. tanh x 是单调递增函数 【答案】A 【解析】 【分析】考虑函数的值域可判断A，根据函数的奇偶性定义判断B，由复合函数的单调性分析可判断D，由 D结合周期定义判断C. ex ex 2ex 2 【详解】由tanh(x) 1 1 ， ex ex ex ex e2x 1 2 2 因e2x 11，则0  2，可得11 1 ，即tanh(x)(1,1)，故A错误； e2x 1 e2x 1 ex ex ex ex 因为tanh(x)的定义域为R，且tanh(x)  tanh(x)，所以tanh(x)是奇函数， ex ex ex ex 故B正确； ex ex 2 1 tanh(x) 1 ，因e2x是增函数，e2x 1是增函数且恒为正数，则 是减函数，故 ex ex e2x 1 e2x 1 tanh(x)是增函数，故D正确； 由D可知函数在R 上单调递增，所以当T 0时，tanh(xT)  tanh  x  ，所以函数不是周期函数，故C 正确. 故选：A7. 已如A是函数 f  x  x2lnx图像上的动点，B是直线x y20上的动点，则A,B两点间距离 AB 的最小值为（ ） A. 4 2 B.4 C. 2 2 D. 5 【答案】C 【解析】 【分析】先求函数 f  x  斜率为1的切线，然后切线与直线x y20的距离即为所求. 2 【详解】因为 f x x2lnx ，（x0），所以 f x 1 ， x 由 f x 1，得x 1，又 f  1 1， 所以 f  x  过  1,1  点的切线为： y1 x1  即x y20. 4 直线x y20与x y20的距离为：d   2 2即为所求. 2 故选：C a 8. 设等差数列  a  的前n项和为S ，公差为d 0, 10 1，则下列结论正确的是（ ） n n a 11 A. a a a  0 B. 使得S 0成立的最小自然数n是20 4 5 18 n S S S S C. 9  10 D. 21  22 9 10 a a 21 22 【答案】C 【解析】 【分析】根据题意可知数列单调递减且a 0,a 0,a a 0，由通项公式化简可判断A，由等差数 10 11 10 11 S  列的性质及求和公式结合条件可判断B，根据 n为递减数列即可判断C，由a ,S 的关系及S S 的符  n  n n 20, 22 号可判断D. a 【详解】由公差为d 0, 10 1可知，等差数列  a  为递减数列且a 0,a 0,a a 0， a n 10 11 10 11 11 对A，a a a 3a 24d 3a 0，故A错误； 4 5 18 1 9 20(a a ) 对B，因为a a 0，所以a a a a  0，所以S  1 20 0，故B错误； 10 11 1 20 10 11 20 2n(n1) na  d d S  对C，因为S n n  1 n 2  d 2 na 1  d 2 ，且 2 0，所以由一次函数单调性知  n n  为单调递减数列， S S 所以 9  10 ，故C正确； 9 10 对D，由B知S 0，且S 21a 0，所以S S a 0， 20 21 11 22 21 22 S S S S S S S S 因为 21  21 ， 22  22 ，若 21  22 ，则 21  22 ，且 a S S a S S a a S S S S 21 21 20 22 22 21 21 22 21 20 22 21  S S  S S 0， 21 20 22 21 即S  S S S  S S  ，即S2 S S ，而S 0，S 0， 21 22 21 22 21 20 21 22 20 20 22 S S 显然矛盾，故 21  22 不成立，故D错误. a a 21 22 故选：C 二､多选题：本题共 3小题，每小题 6分，共 18分.在每小题给出选项中，有多项符合题目要 求.全部选对的得 6分，部分选对的得部分分，有选错项得 0分. 9. 已知a,bR，且ab，a,b,c都不为0，则下列不等式一定成立的是（ ） 1 1 A.  B. ac bc a b a b 1 a 1 b C.  D.      c2 c2 2 2 【答案】BC 【解析】 【分析】由不等式的性质和函数单调性，判断选项中的不等式是否成立. 1 1 【详解】当a0b时，有  ，A选项错误； a b ab，则  ac  bc ab 0，得ac bc，B选项正确； a b ab a b ab，   0，得  ，C选项正确； c2 c2 c2 c2 c2 x a b 1 1 1 函数 y    在R上单调递减，ab，则      ，D选项错误. 2 2 2 故选：BC 10. 已知正数a,b满足4abab5，则下列结论正确的是（ ）A. ab的最大值为1 B. 4ab的最小值为4 1 1 10 C. 16a2 b2的最小值为9 D.  的最小值为 a1 b 9 【答案】ABD 【解析】 【分析】根据均值不等式分别建立不等式解不等式可判断AB，先变形16a2 b2为关于ab的二次函数求最 1 1 值判断C，利用条件变形可得  a1  (b4)9，转化  为关于b的式子由均值不等式判断D. a1 b 【详解】由正数a,b满足4abab5，可得4ab5ab4 ab，解得0 ab 1，即ab1， 1 当且仅当4a b，即a  ,b2时等号成立，故A正确； 2 1 1 4ab 2 由正数a,b满足4abab5，可得4ab5 4ab    ， 4 4  2  1 解得4ab4或4ab20（舍去），当且仅当4a b，即a  ,b2时等号成立，故B正确； 2 16a2 b2 (4ab)2 8ab 5ab 2 8ab ab9 2 56，由A知ab1， 由二次函数的单调性知 ab9 2 56(19)2 568，即ab1时，16a2 b2的最小值为8，故C错误； 1 b4 b 4 由4abab5可得4a4bab9，即  a1  (b4)9，所以    ， a1 9 9 9 1 1 b 1 4 b 1 4 10 b 1 2 所以      2    ，当且仅当  ，即b 3，a  时等号成立，故D正 a1 b 9 b 9 9 b 9 9 9 b 7 确. 故选：ABD 11. 记方程xex 1的实数解为Ω（Ω是无理数），Ω被称为在指数函数中的“黄金比例”.下列有关Ω的结论 正确的是（ ） A. lnΩΩ0 1 1 B. Ω  ,  3 2 C. Ω2 2Ω10 1lnx D. 函数 f  x ex  的最小值为 f  Ω  x 【答案】ACD 【解析】【分析】构建g  x  xex 1，利用导数判断其单调性，结合零点存在性定理分析判断B选项，对于A： 对e 1，Ω 0.5,1  ，取对数整理即可；对于 C：根据二次函数单调性判断；对于D：结合不等式 xlnx10分析可知 f  x 1，当且仅当xex 1时，等号成立. 【详解】构建g  x  xex 1，则Ω为g  x  的零点， 因为g x  x1  ex， 若x1，则g x 0，可知g  x  在 ,1  内单调递减，且g  x 0， 所以g  x  在 ,1  内无零点； 若x1，则g x 0，可知g  x  在 1, 内单调递增， g  0.5  e 10且g  1 e10，所以g  x  在 1, 内存在唯一零点Ω 0.5,1  ； 2 1 对于选项A：因为e 1，Ω 0.5,1  ，即 e，  1 两边取对数可得：ln lne ，lnΩΩ0，故A正确；  对于选项B：由上可知Ω 0.5,1  ，故B不正确； 对于选项C： y  Ω2  2Ω1对称轴为Ω  1，而Ω 0.5,1  ，故 y  Ω2  2Ω1单调递增， 当Ω0.5，y  Ω2  2Ω1最小值为0.25，所以Ω2 2Ω10，故C正确； 1 对于选项D：构建h  x  xlnx1,x0，则h x 1 ， x 令h x 0，解得x1；令h x 0，解得0 x 1； 可知h  x  在  0,1  内单调递减，在  1, 内单调递增， 则h  x h  1 0，可得xlnx10，当且仅当x 1时，等号成立， t 0可得tlnt10，令t  xex，     xex ln xex 10,xex  lnxlnex 10,xex lnxx10,xex lnx1 x xex-lnx1 x 则 f  x   1， x x 1 当且仅当xex 1，即ex  时，等号成立， x  所以 f x 的最小值为 f (Ω)，故D正确； 故选：ACD. 【点睛】方法点睛：对于函数零点的个数的相关问题，利用导数和数形结合的数学思想来求解．这类问题 求解的通法是： （1）构造函数，这是解决此类题的关键点和难点，并求其定义域； （2）求导数，得单调区间和极值点； （3）数形结合，挖掘隐含条件，确定函数图象与x轴的交点情况进而求解． 三､填空题：本题共 3小题，每小题 5分，共 15分. f  x 1,x0 12. 已知函数 y f  x  是R上的奇函数，g  x  ，则g  g  0  __________. 3x 1,x0 【答案】2 【解析】 【分析】根据奇函数的定义得出 f(0)0，再由g(x)解析式得解. 【详解】因为函数 y f  x  是R上的奇函数，所以 f(0)0， 所以g  g  0  g  f  0 1  g(1)312， 故答案为：2 1 nπ 13. 数列  a  的前n项和为S ，若a  sin ，则S __________. n n n n  n1  2 2024 2024 【答案】 2025 【解析】  nπ 【分析】先按通项进行分组求和，再由分式数列用裂项法求和，而数列sin 是周期为4的数列，所以  2  按每4个数一组求和即可. 1 nπ 1 1 nπ 【详解】由a  sin   sin 得： n n  n1  2 n n1 2 1 1  1 1  1 1  1 1   1 1  S    1    0    1    0    0 2024 1 2  2 3  3 4  4 5  2024 2025  1 1 1 1 1 1 1 1 1 1  1 2024               1 01 0 0  1  ， 1 2 2 3 3 4 4 5 2024 2025 2025 20252024 故答案为： . 2025 14. 已知定义在R上的函数 f  x  满足 f  x1  f  x2  ，当x 0,3  时， f  x  x2 3x1 ，则 ex y f  x  在 1012,1012  上的零点个数为__________个. 【答案】1350 【解析】   【分析】由题意可得函数为周期函数，再由一个周期内 0,3 内有两个零点，且一个零点小于1，一个大于 2，即可得出在 1012,1012  上的零点个数. 【详解】由 f  x1  f  x2  可得 f(x) f(x3)， 所以周期T 3， 当x 0,3  时， f  x  x2 3x1 ，令 f  x 0， ex 3 5 3 5 解得x   0,1  ,x   2,3 ，即一个周期内有2个零点， 1 2 2 2 因为 f(1012) f(33731)， 所以 y f  x  在 1012,1012  上的零点个数为2 23371 1350 . 故答案为：1350 四､解答题：本题共 5小题，共 77分.解答应写出文字说明､证明过程或演算步骤. 15. 已知函数 f  x ax3bx2 xR  的图象过点P 1,2  ，且在点P处的切线恰好与直线 3x y40平行.   （1）求函数 f x 的解析式； （2）求 f  x  在 4,1  上的最大值和最小值. 【答案】（1） f  x  x33x2 （2）最大值为4；最小值为：16 【解析】 【分析】（1）根据函数的图象过点P，得到关于a,b的一个关系式，再根据函数在x=1处的导数为3，又得到关于a,b的一个关系式，可求a,b的值. （2）利用导数分析函数的单调性，可求函数的最大、最小值. 【小问1详解】 因为函数 f  x ax3bx2的图象过点P 1,2  ， 所以ab2. 又因为 f x 3ax2 2bx，且 f  x  在点P处的切线恰好与直线3x y40平行， 所以 f1 3a2b3， ab 2 a 1 由 得： ，所以 f  x  x33x2 . 3a2b3 b3 【小问2详解】 由（1）知： f x 3x2 6x 3x  x2  ， 由 fx0 2 x0，由 f ¢( x )>0  x<2或x0. 所以 f  x  在 4,2  上单调递增，在 2,0  上单调递减，在  0,1  上单调递增， 又 f 4 16， f 2 4， f  0 0， f  1 4， 所以 f  x  在 4,1  上的最大值为4，最小值为16. 16. 已知等差数列  a  的公差d 0,a 5,a ,a ,a 成等比数列，数列  b  的前n项和公式为 n 4 1 3 7 n S 2b 2  nN* . n n     （1）求数列 a 和 b 的通项公式： n n （2）设c a b ，求数列  c  的前n项和T . n n n n n 【答案】（1）a n1，b 2n n n （2）T n2n1 n 【解析】 【分析】（1）根据等差数列的通项公式求等差数列的通项公式，根据数列的前n项和，求数列  b  的通项 n 公式. （2）利用错位相减求和法求数列的前n项和.【小问1详解】 由题意：a a 3d 53d ，a a d 5d ，a a 3d 53d ， 1 4 3 4 7 4 因为a ,a ,a 成等比数列， 1 3 7 所以a2 a a   5d 2  53d  53d   d  0 或d 1， 3 1 7 又d 0，所以d 1，所以a 53d 2. 1 所以a n1. n 对数列  b  ：当n 1时，b 2b 2  b 20， n 1 1 1 当n2时，S 2b 2，S 2b 2， n n n1 n1 两式相减得：b 2b 2b  b 2b ， n n n1 n n1 所以  b  是以2为首项，2为公比得等比数列，所以b 2n . n n 【小问2详解】 由（1）知：c  n1 2n， n 所以：T 221322 423 n1 2n， n 2T 222 323424 n2n  n1 2n1， n 两式相减得：T 4  22 232n   n1 2n1 n 22  12n1  4  n1 2n1 n2n1， 12 所以T n2n1 . n 17. 已知函数 f  x  为二次函数，有 f 1 0, f  4 5，__________，从下列条件中选取一个，补全到 1  3  题目中，① f  x  f  x ，②函数 f  x1  为偶函数，③ f  2 3 2  2    （1）求函数 f x 的解析式； （2）若g  x log  x23  log  x1  ，若对任意的x  1,2  ，总存在x 1,2  ，使得 2 2 1 2 g  x  f  x mx 成立，求实数m的取值范围. 2 1 1【答案】（1） f  x  x2 2x3 （2）  5, 【解析】 【分析】（1）用待定系数法求函数解析式. （2）分别求函数的值域，根据两个函数值域之间的关系求参数. 【小问1详解】 abc  0 设 f xax2 bxca 0，由题意： ， 16a4bc 5 两式相减的：3ab1 b 若选①，则：抛物线的对称轴为：x 1，即 1 2ab0. 2a a1  所以b2，所以 f  x  x2 2x3；  c3 若选②，则：抛物线的对称轴为：x 1，同上； abc0 a1   若选③，则：4a2bc3，由16a4bc5 ，得：b2，所以 f  x  x2 2x3.   4a2bc3 c3 综上： f  x  x2 2x3 【小问2详解】   对g x ： 2x 1 2x  x1   x2 3  x2 2x3  x3  x1  g x       x2 3  ln2  x1  ln2  x2 3  x1  ln2  x2 3  x1  ln2  x2 3  x1  ln2 当x1,2  时，由g x 01 x2；由g x 0 1 x 1； 所以g  x  在 1,1  上单调递减，在  1,2  上单调递增， 所以x1,2  时，g  x  g  1 log 4log 21. 2 2 当x 1,2 时， f  x mx x2  m2  x31恒成立， 4x2 4 所以m2  x 在1,2上恒成立. x x4 4  观察可知，函数 y  x在1,2上单调递减，所以 x  413， x  x  max 由m23  m5. 所以实数m的取值范围是：  5, 18. 已知函数 f  x  xlnxax2, f  x  为 f  x  的导函数，记g  x  f x  ，其中a为常数.   （1）讨论g x 的单调性； （2）若函数 f  x  有两个极值点x ,x  x  x  ， 1 2 1 2 ①求a的取值范围； 1 ②求证：x x  . 1 2 a  1 【答案】（1）见解析 （2）①0, ；②证明见解析  2 【解析】 【分析】（1）求出g x  ，分类讨论，利用g(x)0，g(x)0解不等式即可得解； （2）①先分析a0不合题意，再求出a0时函数 f  x  在有两个极值点x ,x  x  x  的必要条件，再 1 2 1 2 x 2  x x  此条件下分析即可得解；②对结论进行转化，只需证ln 1  1 2 ，换元后利用导数确定函数单调性， x x x 2 1 2 得出函数最值，即可得证. 【小问1详解】 定义域为(0,).  f(x)lnx12ax，g(x)lnx12ax， 1 12ax g x  2a  ， x x 当a0时， 恒成立，g(x)在(0,)上单调递增， ′ ( )>0 1 当a0时，令g(x)0，则12ax0，解得x ， 2a 1 令g(x)0，则12ax0，解得x ， 2a  1   1  g(x)在0, 单调递增，在 , 单调递减.  2a 2a 综上，当a0时，g(x)在(0,)上单调递增；  1   1  当a0时，g(x)在0, 单调递增，在 , 单调递减.  2a 2a  【小问2详解】 由（1）知，a0时， f(x)0最多一个根，不符合题意，故a0， 函数 f  x  有两个极值点x ,x  x  x  ， 1 2 1 2 g(x)0在  0, 有两个不同零点的必要条件是 ， 1 1 1 2 =ln2 >0 解得0a ， 2 1  1   1  当0a ，g(x)在0, 单调递增，在 , 单调递减， 2  2a 2a  ， 1 1 1 2 2 =ln2 >0, e =− e <0, →+∞, →−∞ 1 1   1  由零点存在性定理得： f(x)在 , ， , 各有1个零点， e 2a 2a   1 a的取值范围是0, .  2 ②函数 f  x  有两个极值点x ,x  x  x  ， 1 2 1 2 lnx 12ax 0① 1 1 lnx 12ax 0② 2 2 lnx lnx ①②得：a  1 2 ， 2  x x  1 2 1 2  x x  要证x x  ，即证 ，即证lnx lnx  1 2 ， 1 2 a 2 1− 2 1 2 x 1 x 2 1+ 2 >ln 1−ln 2 x 2  x x  即证ln 1  1 2 ， x x x 2 1 2 令t  x 1  0t 1  ，则lnt  2  t1  ， x t1 2 2  t1  令R  t lnt ，则 ， t1 2 ′ 1 4 −1 2 2 = − +1 = +1 >0y  R(t)在(0,1)上单调递增，R  t R  1 0， 2  t1  lnt 0在(0,1)上成立， t1 1 x x  ，得证. 1 2 a 1 【点睛】关键点点睛：要证明不等式x x  ，关键点之一在于消去a后对结论进行恰当变形，转化为 1 2 a 证明ln x 1  2  x 1 x 2  成立，其次关键点在于令t  x 1  0t 1  换元，转化为证明lnt  2  t1  成立. x x x x t1 2 1 2 2 19. 若在数列的每相邻两项之间插入此两项的和，形成新的数列，再把所得数列按照同样的方法不断构造出 新的数列.现对数列1，3进行构造，第一次得到数列1，4，3：第二次得到数列1,5,4,7,3：依次构造，第 n  nN* 次得到的数列的所有项之和记为a ，如a 1438. n 1 （1）求a ； 3   （2）求 a 的通项公式； n 1 1 1 1 5 （3）证明：     a a a a 24 . 1 2 3 n 【答案】（1）a 56 3 （2）a 23n 2 n （3）证明见解析 【解析】 【分析】（1）求出第三次得到数列再求和即可； （2）设出第n次构造后得到的数列求出a ，则得到第n1次构造后得到的数列求出a ，可得a 与a 关 n n1 n1 n 系，再利用构造法求通项即可； （3）利用放缩法求等比数列和可得答案. 【小问1详解】 因为第二次得到数列1,5,4,7,3，所以第三次得到数列1,6,5,9,4,11,7,10,3 所以a 1659411710356 ； 3 【小问2详解】设第n次构造后得的数列为1,x ,x ,,x ,3，则a 1x x x 3， 1 2 k n 1 2 k 则第n1次构造后得到的数列为 1,1x ,x ,x x ,x ,,x x ,x ,x 3,3 ， 1 1 1 2 2 k1 k k k 则a 11x x x x x x x x x 33 n1 1 1 1 2 2 k1 k k k 83  1x x x x 3 1243a ， 1 2 k1 k n a 2 a 23  a 2  ，可得 n1 3，a 26， n1 n a 2 1 n 所以  a 2  是以3为公比，6为首项的等比数列， n 所以a 263n1，即a 23n 2； n n 【小问3详解】 1 1 1 1 1 1 由（2）得      ， a 63n12 2 3n 1 2 3n n 1 1 5 所以当n 1时，   ， a 8 24 1 1 1 1 1 1 1 1 1 1  当n2时，所以          a a a a 8 232 33 3n  1 2 3 n 1  1  1  1 1 32  3n1  5 1 1 5       ， 8 2 1 24 12 3n1 24 1 3 1 1 1 1 5 综上所述，     . a a a a 24 1 2 3 n 【点睛】关键点点睛：（2）问中解题关键点是已知相邻两项关系构造等比数列，进而得到数列的通项公式； （3）问中根据的通项公式，应用放缩变成等比数列的前项和，应用公式计算即可.