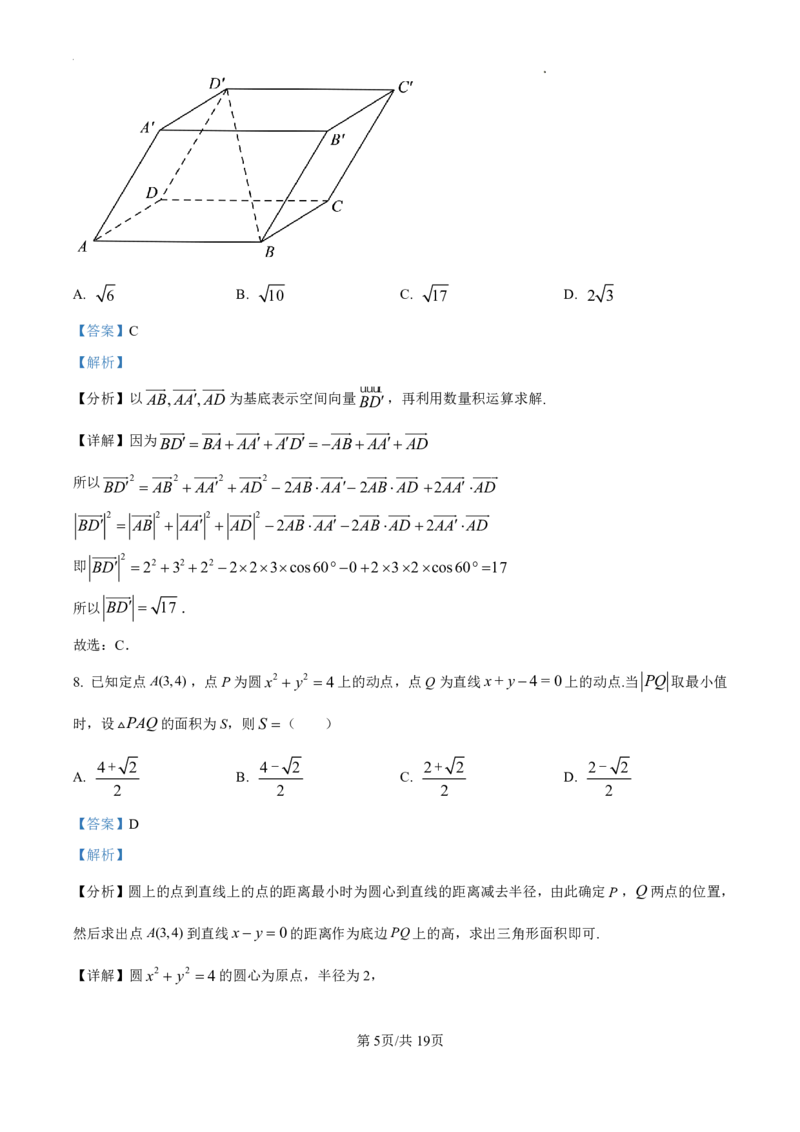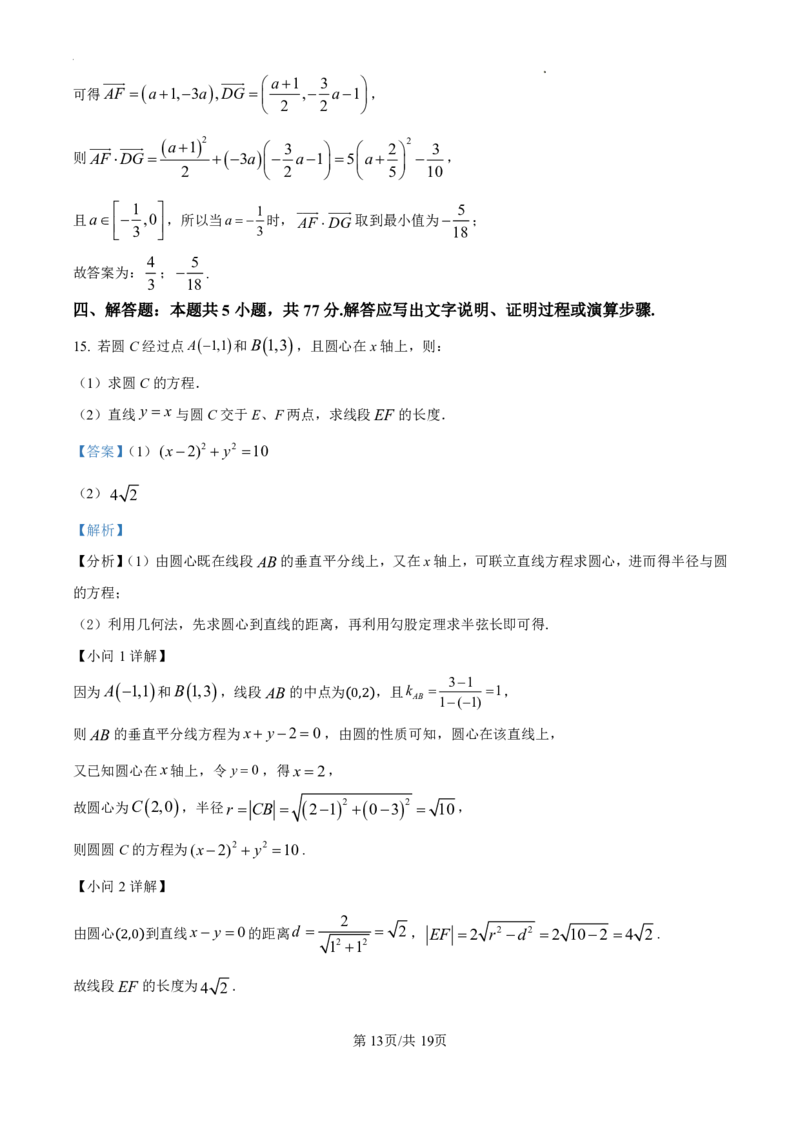数学-陕西省咸阳市实验中学2024-2025学年高二上学期10月月考_2024-2025高二（7-7月题库）_2024年10月试卷_1012陕西省咸阳市实验中学2024-2025学年高二上学期10月月考

咸阳市实验中学 2024~2025 学年度第一学期第一次月考
高二数学试题
注意事项：
1.本试题共 4页，满分 150分，时间 120分钟.
2.答卷前，考生务必将自己的姓名、班级和准考证号填写在答题卡上.
3.回答选择题时，选出每小题答案后，用 2B 铅笔把答题卡上对应题目的答案标号涂黑如需改
动，用橡皮擦干净后，再选涂其它答案标号.回答非选择题时，将答案写在答题卡上.写在本试
卷上无效.
4.考试结束后，监考员将答题卡按顺序收回，装袋整理：试题不回收.
第I 卷（选择题 共58分）
一、选择题：本题共 8小题，每小题5分，共 40分.在每小题给出的四个选项中，只有一项是
符合题目要求的.
3x y30
1. 直线 的倾斜角是（ ）
A. 30 B. 60 C. 120 D. 150
2. 在空间直角坐标系Oxyz中，点  1,2,3  关于x轴对称的点为（ ）
A.  1,2,3  B. 1,2,3  C. 1,2,3  D. 1,2,3 
3. 已知两点A  1，3  ，B  4，2  ，直线l ：kx y3k10线段AB相交，则k的取值范围是 （ ）
A. 1k 1 B. k 1或k 1 C. k 1 D. k 1
     
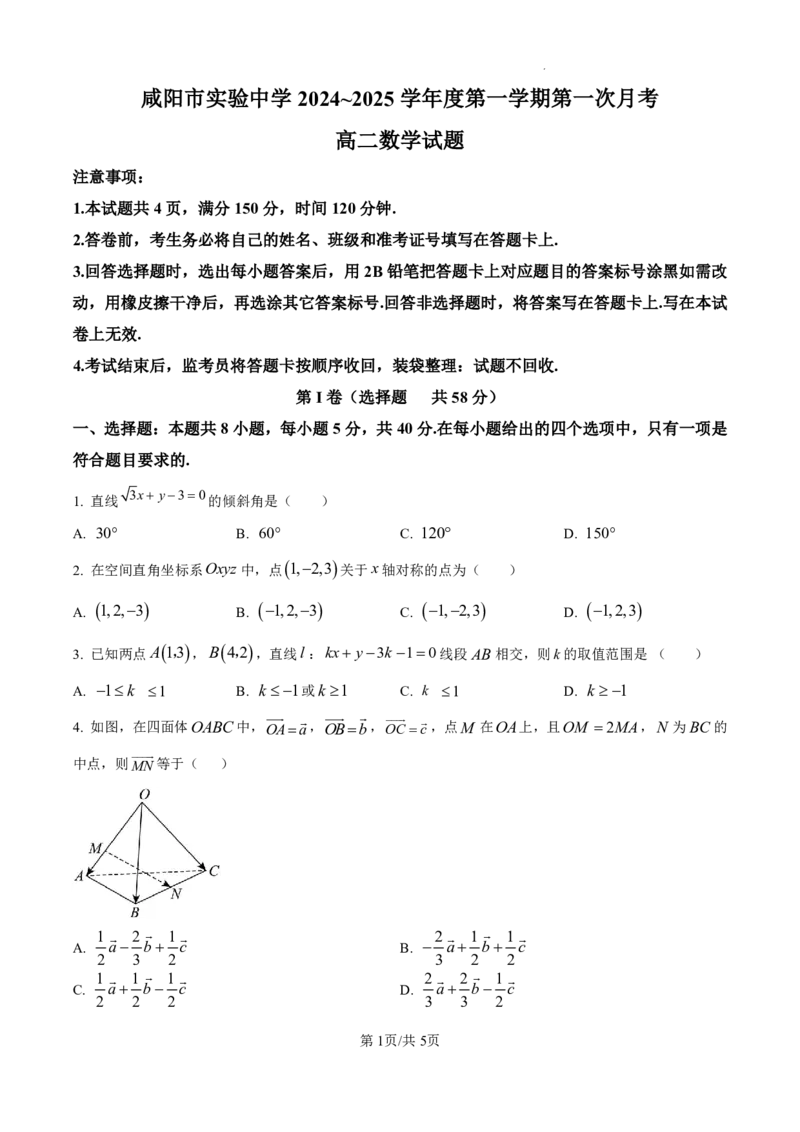
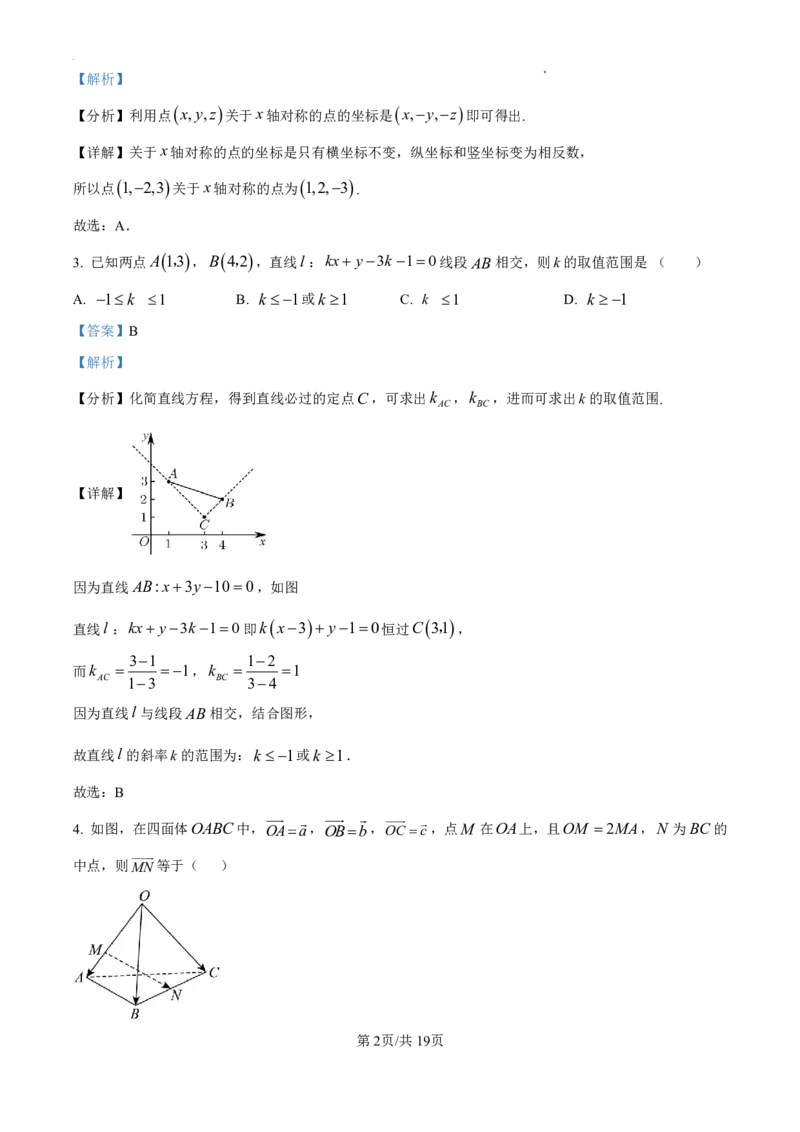
4. 如图，在四面体OABC中，OAa，OBb，OCc，点M 在OA上，且OM 2MA，N 为BC的

中点，则MN等于（ ）
1  2  1  2  1  1 
A. a b  c B.  a b c
2 3 2 3 2 2
1  1  1  2  2  1 
C. a b  c D. a b  c
2 2 2 3 3 2
第1页/共5页
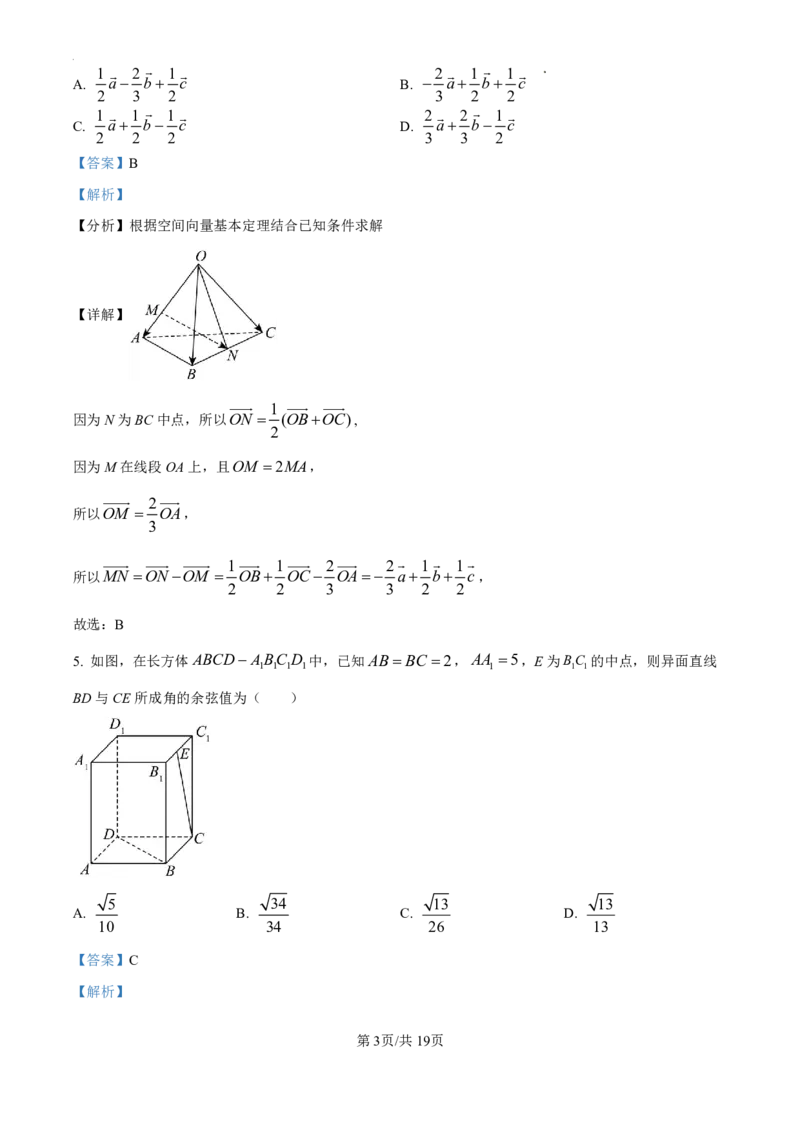
学科网（北京）股份有限公司5. 如图，在长方体ABCDABC D 中，已知AB BC 2，AA 5，E为BC 的中点，则异面直线
1 1 1 1 1 1 1
BD与CE所成角的余弦值为（ ）
5 34 13 13
A. B. C. D.
10 34 26 13
6. 已知直线l ：ax ya 0与l ： a6  x a4  y40，则“a 3”是“l //l ”的（ ）
1 2 1 2
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
7. 平行六面体ABCDABCD的底面ABCD是边长为2的正方形，且AADAAB60，
AA3，则线段BD的长为（ ）
A. 6 B. 10 C. 17 D. 2 3
8. 已知定点A(3,4)，点P为圆x2  y2  4上的动点，点Q为直线x+y4=0上的动点.当 PQ 取最小值
时，设PAQ的面积为S，则S （ ）
4+ 2 4- 2 2+ 2 2- 2
A. B. C. D.
2 2 2 2
二、选择题：本题共 3小题，每小题 6分，共 18分，在每小题给出的选项中，有多项符合题
目要求.全部选对的得6分，部分选对的得部分分，有选错的得 0分.
第2页/共5页
学科网（北京）股份有限公司9. 设l，m，n是不同的直线，α，β是不同的平面，则下列判断错误的是（ ）
A.
若l//，m//，//，则l//m
B
若，l//，m//，则l//m
.
C. 若直线m，n，且l⊥m，l⊥n，则l 
D. 若l，m是异面直线，l ，m，且l//，m//，则//
10. 下列结论正确的是（ ）

A. 向量u  1,2  是直线l:2x y30的一个方向向量；
B.“a1”是“a2x y10与直线xay20互相垂直”的充要条件；
C. 已知直线l过点P(2,4)，且在x,y轴上截距相等，则l的方程为x y60；
D. 直线 y3x2在y轴上的截距为2.
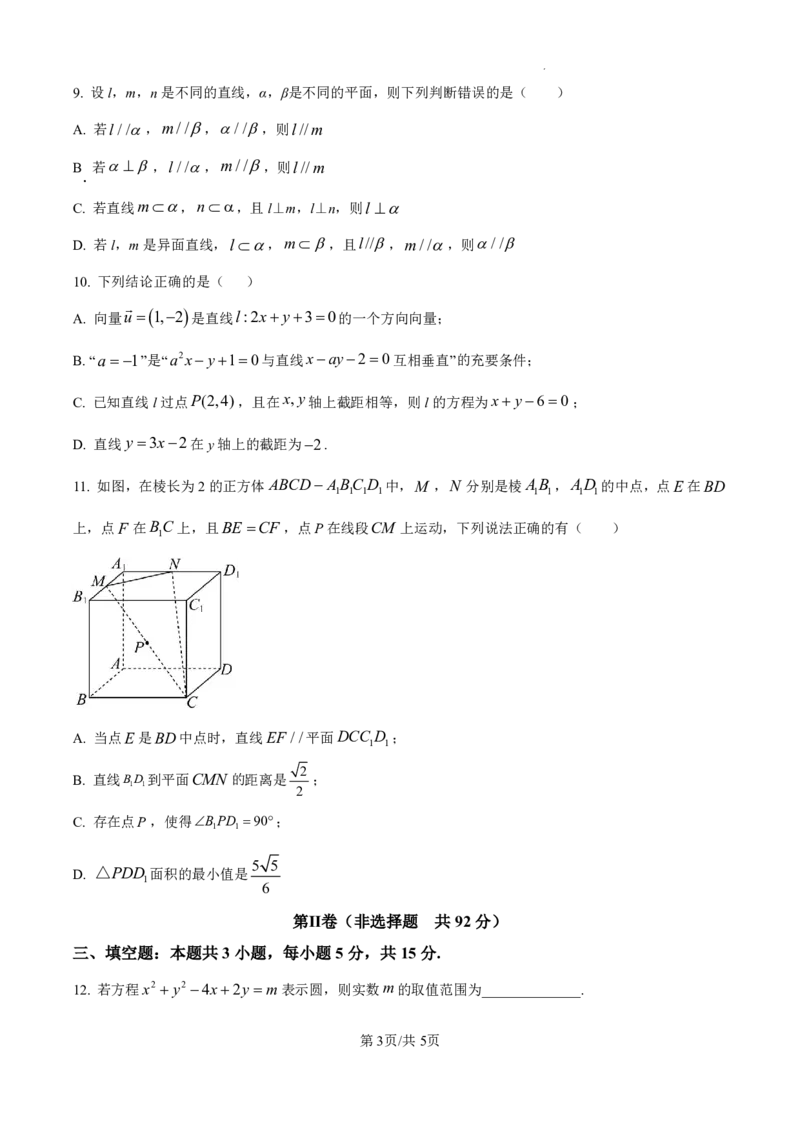
11. 如图，在棱长为2的正方体ABCD ABC D 中，M ，N 分别是棱AB ，AD 的中点，点E在BD
1 1 1 1 1 1 1 1
上，点F 在BC上，且BE CF ，点P在线段CM 上运动，下列说法正确的有（ ）
1
A. 当点E是BD中点时，直线EF //平面DCC D ；
1 1
2
B. 直线BD到平面CMN 的距离是 ；
1 1
2
C. 存在点P，使得BPD 90；
1 1
5 5
D. △PDD 面积的最小值是
1
6
第Ⅱ卷（非选择题 共 92分）
三、填空题：本题共 3小题，每小题 5分，共 15分.
12. 若方程x2  y2 4x2y m表示圆，则实数m的取值范围为______________.
第3页/共5页
学科网（北京）股份有限公司13. 已知在 中，顶点A  4,2  ，点B在直线l：x y20上，点C在x轴上，则 的周长的最

小值______.
uur uur uuur
1
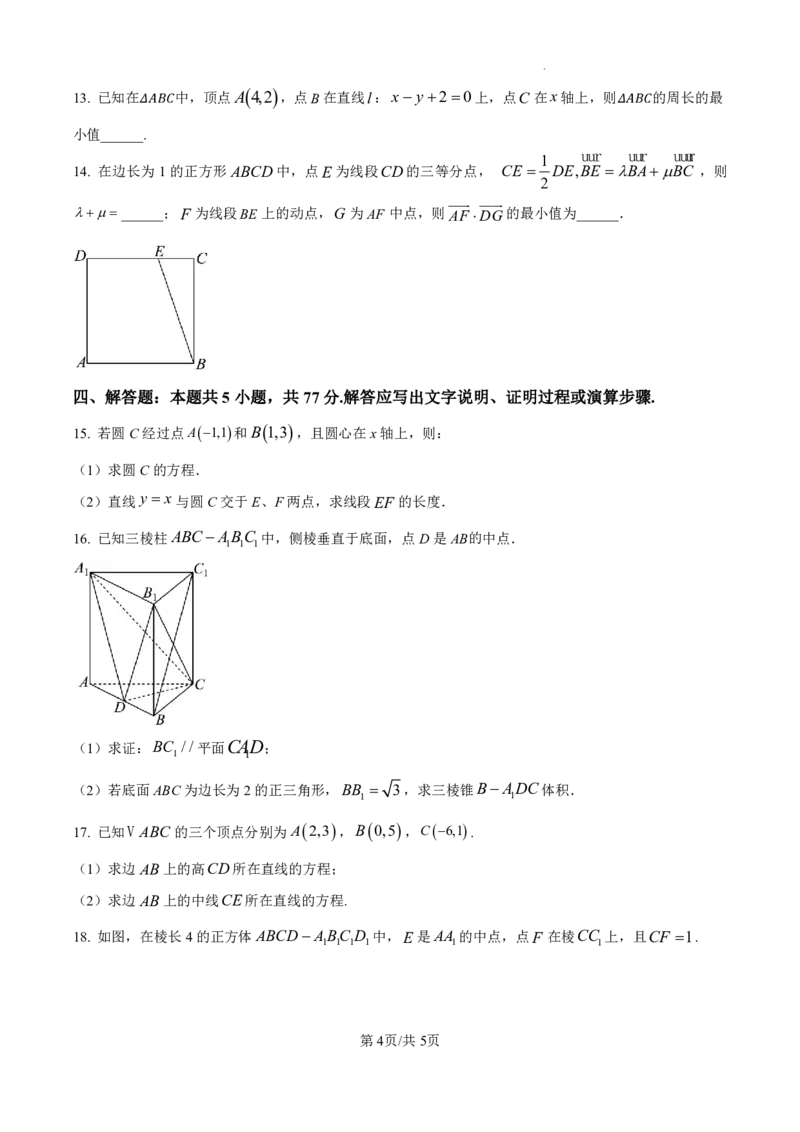
14. 在边长为1的正方形ABCD中，点E为线段CD的三等分点， CE  DE,BE BABC ，则
2
 
______；F 为线段BE 上的动点，G 为AF 中点，则AF DG的最小值为______．
四、解答题：本题共 5小题，共 77分.解答应写出文字说明、证明过程或演算步骤.
15. 若圆C经过点A1,1和B  1,3  ，且圆心在x轴上，则：
（1）求圆C的方程．
（2）直线 y  x与圆C交于E、F两点，求线段EF 的长度．
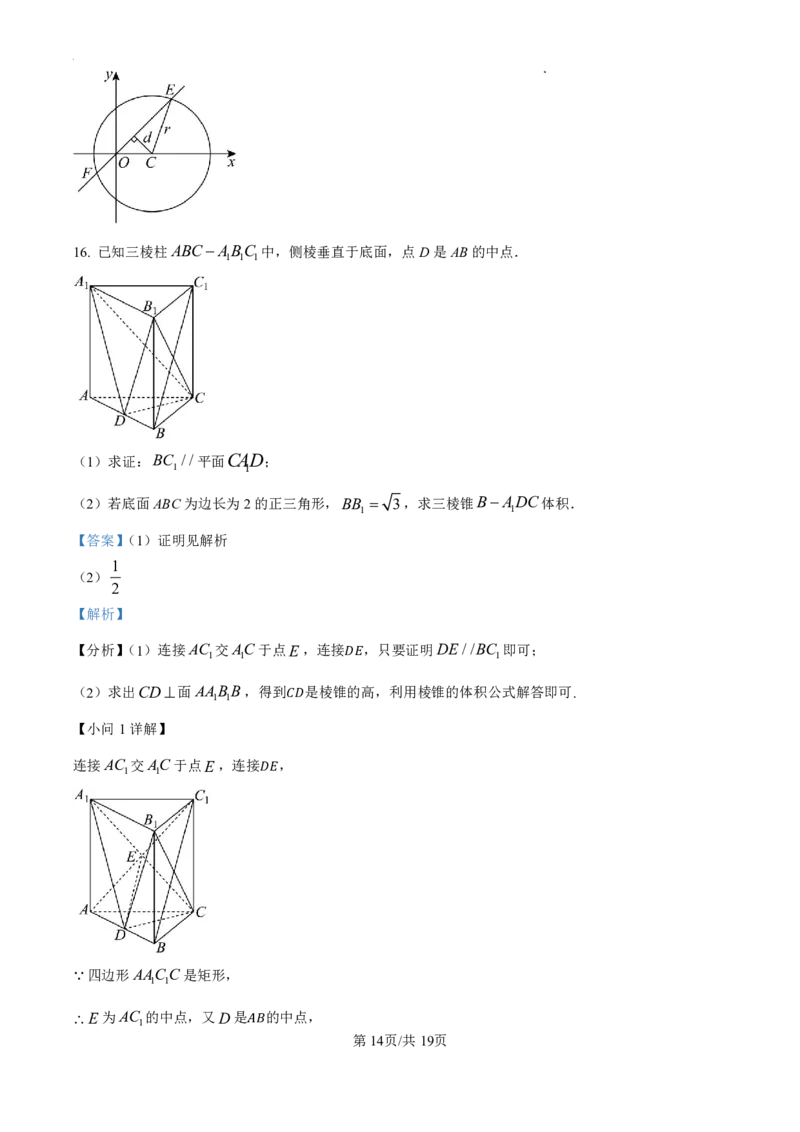
16. 已知三棱柱ABCABC 中，侧棱垂直于底面，点D是AB的中点．
1 1 1
（1）求证：BC //平面CAD；
1 1
（2）若底面ABC为边长为2的正三角形，BB  3，求三棱锥BADC体积．
1 1
17. 已知V ABC 的三个顶点分别为A2,3，B  0,5  ，C6,1 .
（1）求边AB上的高CD所在直线的方程；
（2）求边AB上的中线CE所在直线的方程.
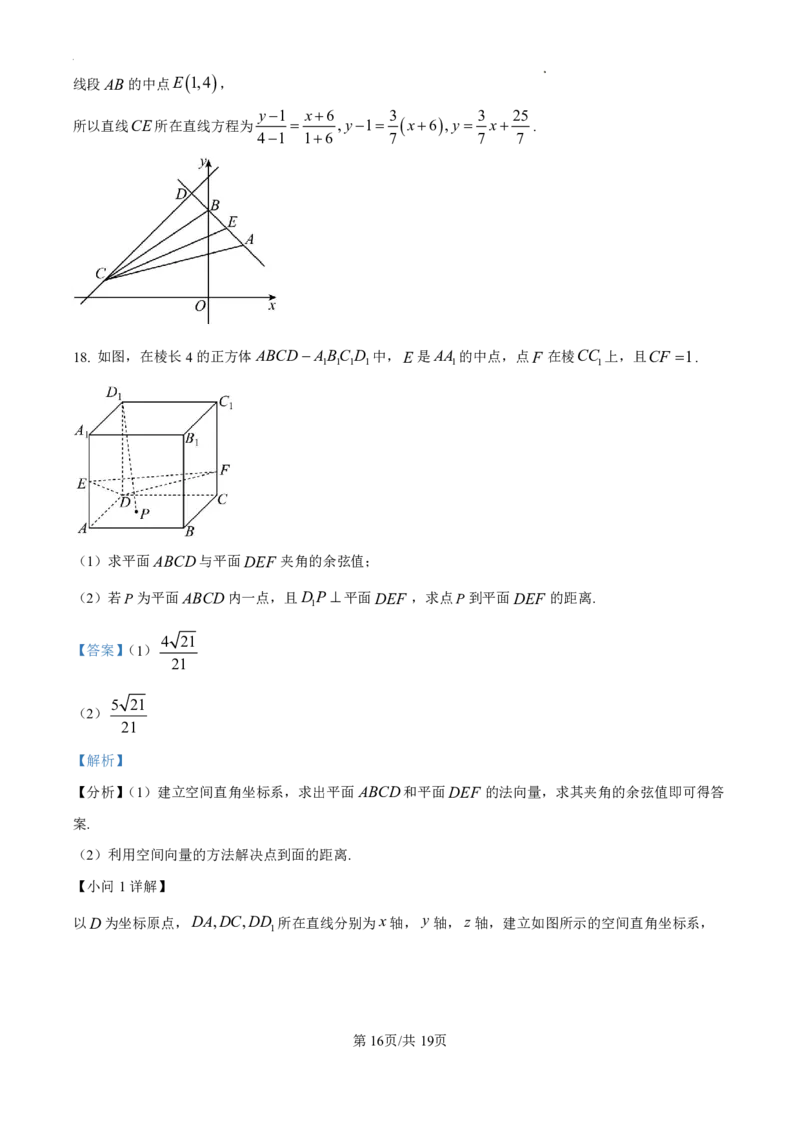
18. 如图，在棱长4的正方体ABCDABC D 中，E是AA 的中点，点F 在棱CC 上，且CF 1.
1 1 1 1 1 1
第4页/共5页
学科网（北京）股份有限公司（1）求平面ABCD与平面DEF 夹角的余弦值；
（2）若P为平面ABCD内一点，且DP 平面DEF ，求点P到平面DEF 的距离.
1
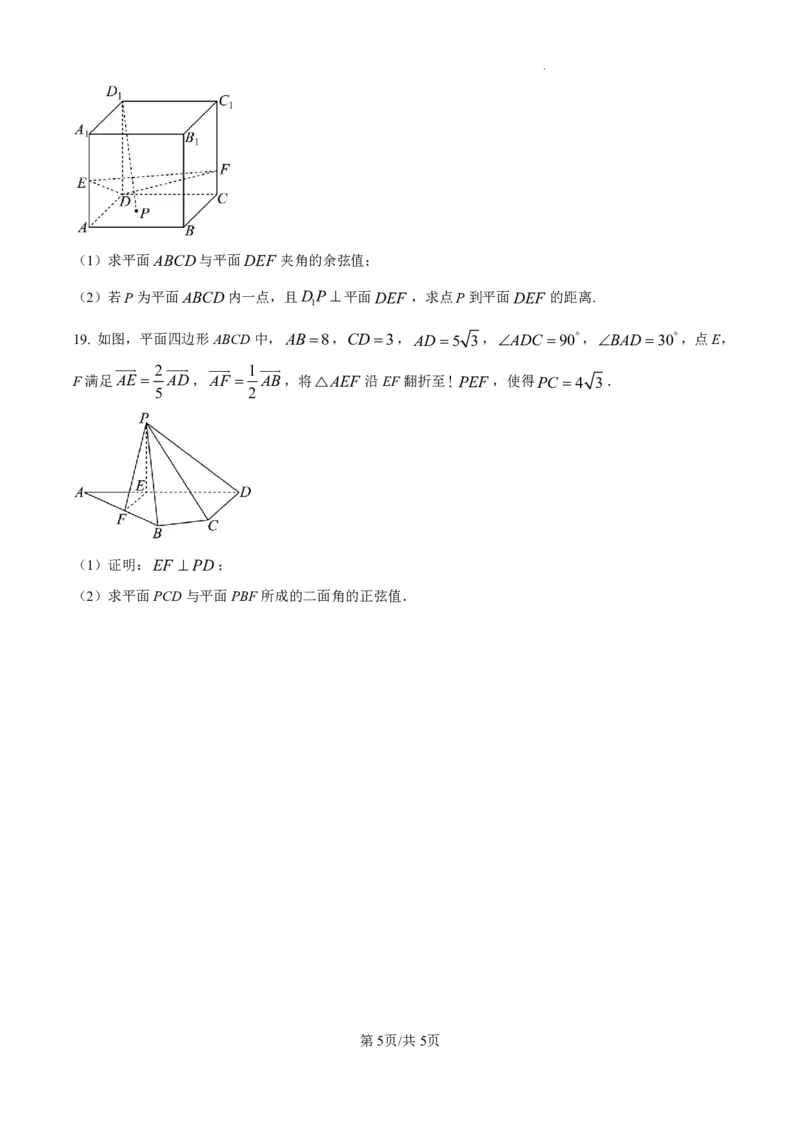
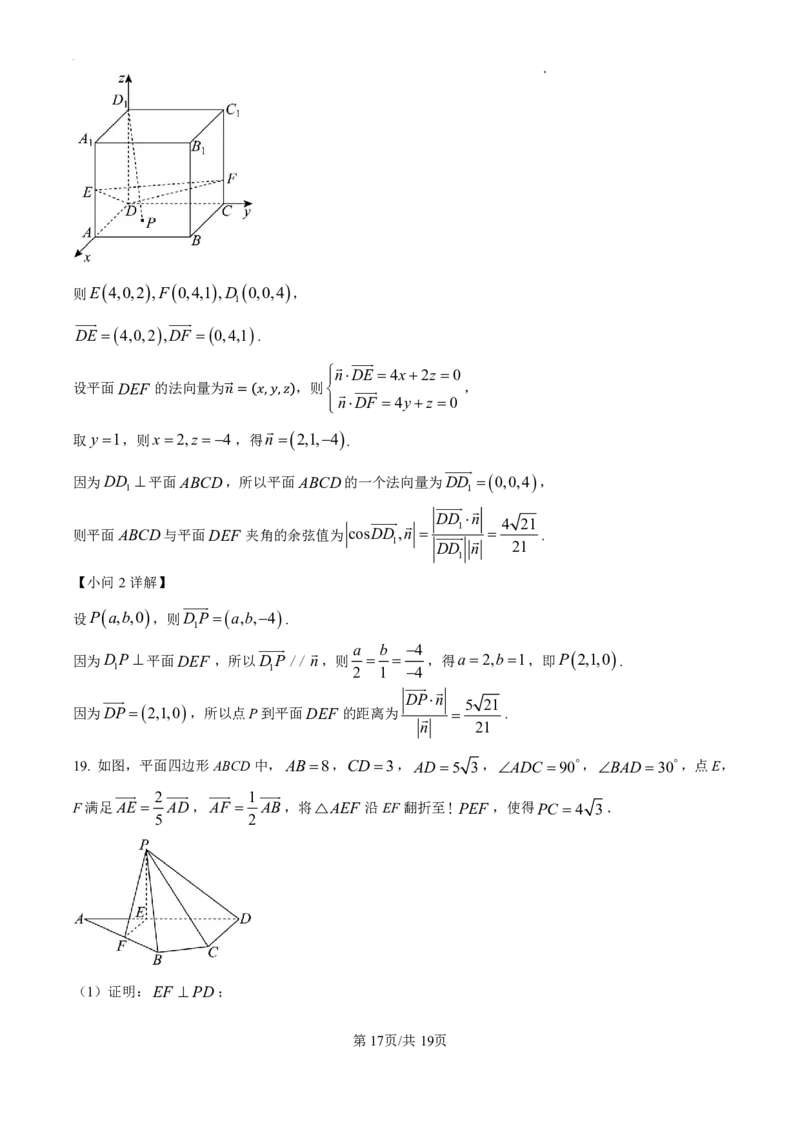
19. 如图，平面四边形ABCD中，AB8，CD3，AD 5 3，ADC 90，BAD 30，点E，
 2  1
F满足AE  AD，AF  AB，将△AEF 沿EF翻折至!PEF ，使得PC 4 3．
5 2
（1）证明：EF PD；
（2）求平面PCD与平面PBF所成的二面角的正弦值．
第5页/共5页
学科网（北京）股份有限公司1
咸阳市实验中学 2024~2025 学年度第一学期第一次月考
高二数学试题
注意事项：
1.本试题共 4页，满分 150分，时间 120分钟.
2.答卷前，考生务必将自己的姓名、班级和准考证号填写在答题卡上.
3.回答选择题时，选出每小题答案后，用 2B 铅笔把答题卡上对应题目的答案标号涂黑如需改
动，用橡皮擦干净后，再选涂其它答案标号.回答非选择题时，将答案写在答题卡上.写在本试
卷上无效.
4.考试结束后，监考员将答题卡按顺序收回，装袋整理：试题不回收.
第I 卷（选择题 共58分）
一、选择题：本题共 8小题，每小题5分，共 40分.在每小题给出的四个选项中，只有一项是
符合题目要求的.
3x y30
1. 直线 的倾斜角是（ ）
A. 30 B. 60 C. 120 D. 150
【答案】C
【解析】
【分析】先得到直线方程的斜率，然后根据k  tan的关系，以及的范围，求出答案.
【详解】因为直线方程是 3x y30，
所以该直线的斜率k  3，
所以可得tan 3 ，
而0,180

所以该直线的倾斜角是120.
故选C
【点睛】本题考查根据直线方程求直线的倾斜角，属于简单题.
2. 在空间直角坐标系Oxyz中，点  1,2,3  关于x轴对称的点为（ ）
A.
 1,2,3 
B.
1,2,3 
C.
1,2,3 
D.
1,2,3 
【答案】A
第1页/共19页
学科网（北京）股份有限公司1
【解析】
【分析】利用点  x,y,z  关于x轴对称的点的坐标是 x,y,z 即可得出.
【详解】关于x轴对称的点的坐标是只有横坐标不变，纵坐标和竖坐标变为相反数，
所以点  1,2,3  关于x轴对称的点为  1,2,3  .
故选：A．
3. 已知两点A  1，3  ，B  4，2  ，直线l ：kx y3k10线段AB相交，则k的取值范围是 （ ）
A. 1k 1 B. k 1或k 1 C. k 1 D. k 1
【答案】B
【解析】
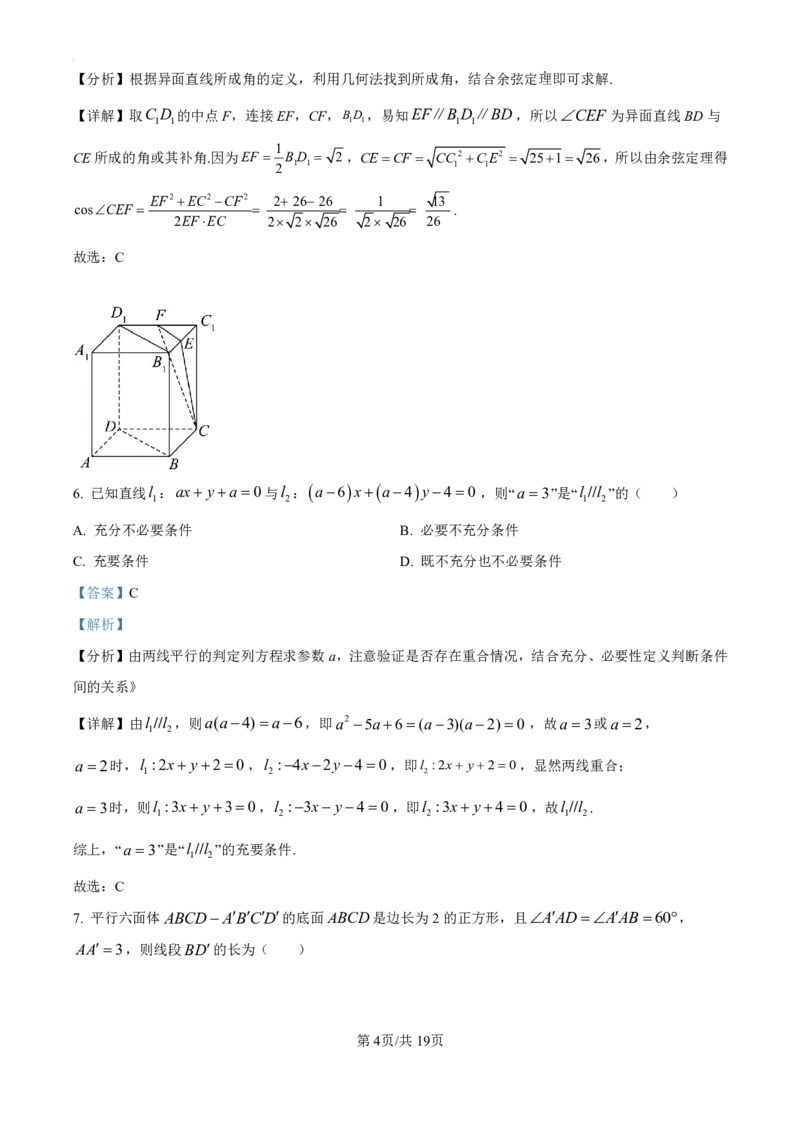
【分析】化简直线方程，得到直线必过的定点C，可求出k ，k ，进而可求出k的取值范围.
AC BC
【详解】
因为直线AB:x3y100，如图
直线l ：kx y3k10即k  x3  y10恒过C  3，1  ，
31 12
而k  1，k  1
AC 13 BC 34
因为直线l 与线段AB相交，结合图形，
故直线l的斜率k的范围为：k 1或k 1．
故选：B
     
4. 如图，在四面体OABC中，OAa，OBb，OCc，点M 在OA上，且OM 2MA，N 为BC的

中点，则MN等于（ ）
第2页/共19页
学科网（北京）股份有限公司1
1  2  1  2  1  1 
A. a b  c B.  a b c
2 3 2 3 2 2
1  1  1  2  2  1 
C. a b  c D. a b  c
2 2 2 3 3 2
【答案】B
【解析】
【分析】根据空间向量基本定理结合已知条件求解
【详解】
 1  
因为N为BC中点，所以ON  (OBOC),
2
因为M在线段OA上，且OM 2MA，
 2
所以OM  OA，
3
   1 1 2 2 1 1
所以MN ON OM  OB OC OA a b c，
2 2 3 3 2 2
故选：B
5. 如图，在长方体ABCDABC D 中，已知AB BC 2，AA 5，E为BC 的中点，则异面直线
1 1 1 1 1 1 1
BD与CE所成角的余弦值为（ ）
5 34 13 13
A. B. C. D.
10 34 26 13
【答案】C
【解析】
第3页/共19页
学科网（北京）股份有限公司1
【分析】根据异面直线所成角的定义，利用几何法找到所成角，结合余弦定理即可求解.
【详解】取C D 的中点F，连接EF，CF，BD ，易知EF∥BD∥BD，所以CEF 为异面直线BD与
1 1 1 1 1 1
1
CE所成的角或其补角.因为EF  BD  2，CECF  CC2CE2  251 26，所以由余弦定理得
2 1 1 1 1
EF2EC2CF2 2 26 26 1 13
cosCEF     .
2EFEC 2 2 26 2 26 26
故选：C
6. 已知直线l ：ax ya 0与l ： a6  x a4  y40，则“a 3”是“l //l ”的（ ）
1 2 1 2
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
【答案】C
【解析】
【分析】由两线平行的判定列方程求参数a，注意验证是否存在重合情况，结合充分、必要性定义判断条件
间的关系》
【详解】由l //l ，则a(a4)a6，即a2 5a6(a3)(a2)0 ，故a 3或a2，
1 2
a2时，l :2x y20，l :4x2y40，即l :2x y20，显然两线重合；
1 2 2
a 3时，则l :3x y30，l :3x y40，即l :3x y40，故l //l .
1 2 2 1 2
综上，“a 3”是“l //l ”的充要条件.
1 2
故选：C
7. 平行六面体ABCDABCD的底面ABCD是边长为2的正方形，且AADAAB60，
AA3，则线段BD的长为（ ）
第4页/共19页
学科网（北京）股份有限公司1
A. 6 B. 10 C. 17 D. 2 3
【答案】C
【解析】
   uuur
【分析】以AB,AA,AD 为基底表示空间向量 BD，再利用数量积运算求解.
      
【详解】因为 BD BA AA ADAB AA AD
         
所以 BD 2  AB 2 AA 2 AD 2 2ABAA2ABAD 2AAAD
         
2 2 2 2
BD  AB  AA  AD 2ABAA2ABAD2AAAD

2
即 BD 22 32 22 223cos600232cos6017

所以 BD  17 ．
故选：C．
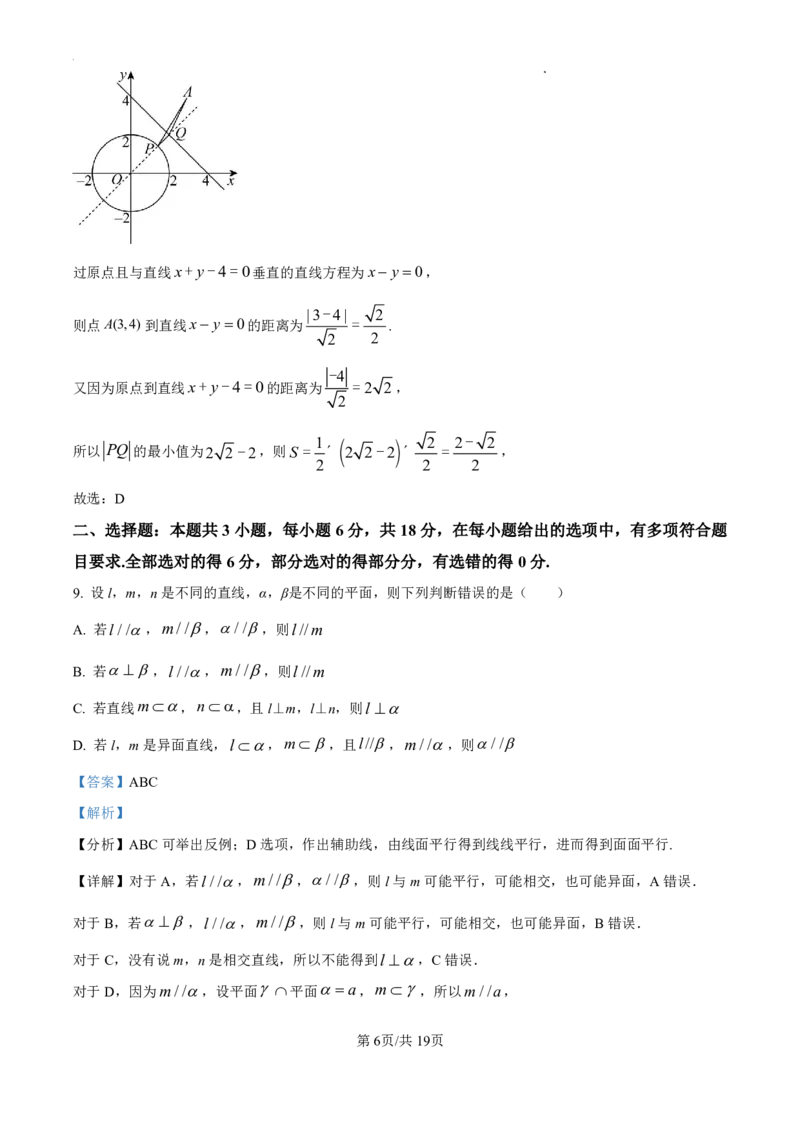
8. 已知定点A(3,4)，点P为圆x2  y2  4上的动点，点Q为直线x+y4=0上的动点.当 PQ 取最小值
时，设PAQ的面积为S，则S （ ）
4+ 2 4- 2 2+ 2 2- 2
A. B. C. D.
2 2 2 2
【答案】D
【解析】
【分析】圆上的点到直线上的点的距离最小时为圆心到直线的距离减去半径，由此确定P，Q两点的位置，
然后求出点A(3,4)到直线x y 0的距离作为底边PQ上的高，求出三角形面积即可.
【详解】圆x2  y2 4的圆心为原点，半径为2，
第5页/共19页
学科网（北京）股份有限公司1
过原点且与直线x+y-4=0垂直的直线方程为x y 0，
|3-4| 2
则点A(3,4)到直线x y 0的距离为 = .
2 2
-4
又因为原点到直线x+y-4=0的距离为 = 2 2，
2
1 ( ) 2 2- 2
所以 PQ 的最小值为2 2-2，则S = ´ 2 2-2 ´ = ，
2 2 2
故选：D
二、选择题：本题共 3小题，每小题 6分，共 18分，在每小题给出的选项中，有多项符合题
目要求.全部选对的得6分，部分选对的得部分分，有选错的得 0分.
9. 设l，m，n是不同的直线，α，β是不同的平面，则下列判断错误的是（ ）
A.
若l//，m//，//，则l//m
B.
若，l//，m//，则l//m
C. 若直线m，n，且l⊥m，l⊥n，则l 
D. 若l，m是异面直线，l ，m，且l//，m//，则//
【答案】ABC
【解析】
【分析】ABC可举出反例；D选项，作出辅助线，由线面平行得到线线平行，进而得到面面平行.
【详解】对于A，若l//，m//，//，则l与m可能平行，可能相交，也可能异面，A错误．
对于B，若，l//，m//，则l与m可能平行，可能相交，也可能异面，B错误．
对于C，没有说m，n是相交直线，所以不能得到l ，C错误．
对于D，因为m//，设平面  平面a，m ，所以m//a，
第6页/共19页
学科网（北京）股份有限公司1
因为l，m是异面直线，l ，所以l，a相交，
因为m//a，m，a  ，所以a//，
因为l//，a//，l，a相交，所以//，D正确．
故选：ABC
10. 下列结论正确的是（ ）

A. 向量u  1,2  是直线l:2x y30的一个方向向量；
B.“a1”是“a2x y10与直线xay20互相垂直”的充要条件；
C. 已知直线l过点P(2,4)，且在x,y轴上截距相等，则l的方程为x y60；
D. 直线 y3x2在y轴上的截距为2.
【答案】AD
【解析】
【分析】结合方向向量的定义，可判定A正确；结合直线垂直的性质与运算，可判定B错误；根据题意，
求得截距相等的直线方程，可判定C错误；根据截距的定义与求解，可判定D正确．

【详解】解：对于A中，直线l:2x y30的斜率为2，所以向量u  1,2  是直线l的一个方向向
量，所以A正确；
对于B中，当直线a2x y10与直线xay20互相垂直，则a2 a 0，
解得a 0或a1，故“a1”是“a2x y10与直线xay20互相垂直”的充分不必要条件，
所以B错误；
对于C中，直线l过点P(2,4)，且在x,y轴上截距相等，当截距为0时，直线方程为 y 2x；
当截距不为0时，可得直线方程为x y60，所以C错误；
对于D中，由y3x2，令x0，可得 y=2，所以y3x2在 y 轴上的截距为2，所以D正确．
故选：AD．
第7页/共19页
学科网（北京）股份有限公司1
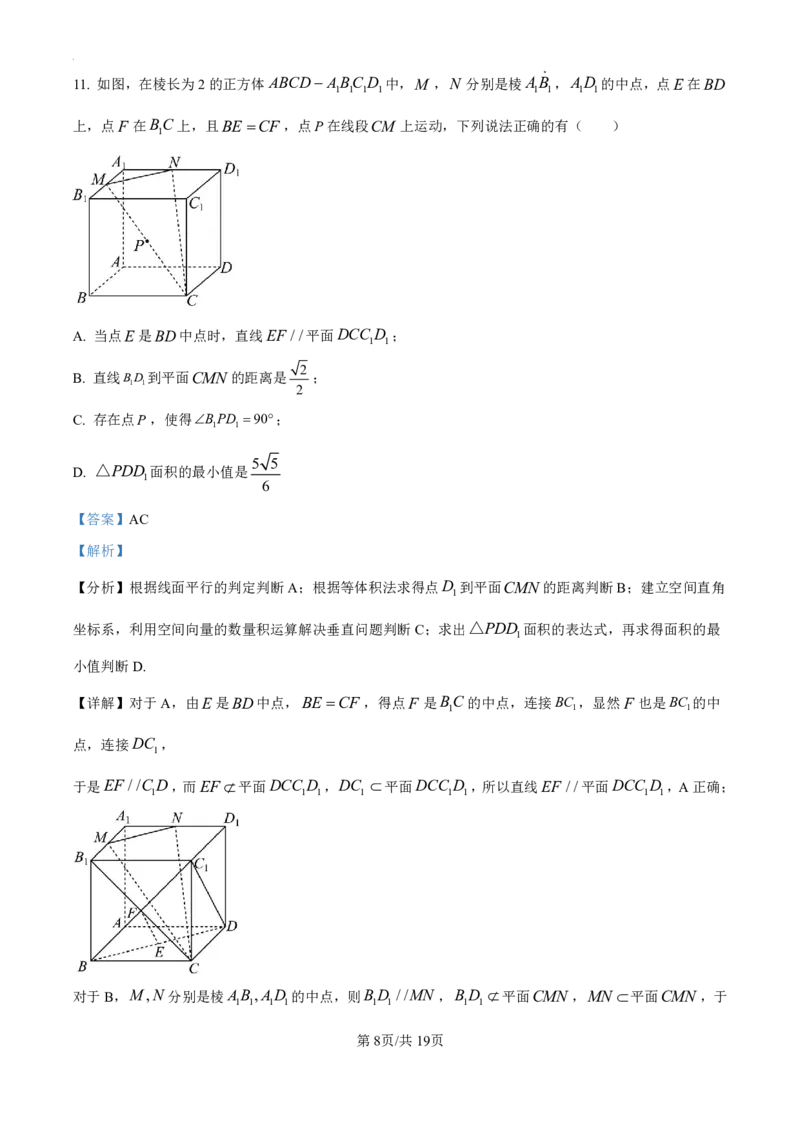
11. 如图，在棱长为2的正方体ABCD ABC D 中，M ，N 分别是棱AB ，AD 的中点，点E在BD
1 1 1 1 1 1 1 1
上，点F 在BC上，且BE CF ，点P在线段CM 上运动，下列说法正确的有（ ）
1
A. 当点E是BD中点时，直线EF //平面DCC D ；
1 1
2
B. 直线BD到平面CMN 的距离是 ；
1 1
2
C. 存在点P，使得BPD 90；
1 1
5 5
D. △PDD 面积的最小值是
1
6
【答案】AC
【解析】
【分析】根据线面平行的判定判断A；根据等体积法求得点D 到平面CMN 的距离判断B；建立空间直角
1
坐标系，利用空间向量的数量积运算解决垂直问题判断C；求出△PDD 面积的表达式，再求得面积的最
1
小值判断D.
【详解】对于A，由E是BD中点，BE CF ，得点F 是BC的中点，连接BC ，显然F 也是BC 的中
1 1 1
点，连接DC ，
1
于是EF //C D，而EF 平面DCC D ，DC 平面DCC D ，所以直线EF //平面DCC D ，A正确；
1 1 1 1 1 1 1 1
对于B，M,N 分别是棱AB ,AD 的中点，则BD //MN ，BD 平面CMN ，MN 平面CMN ，于
1 1 1 1 1 1 1 1
第8页/共19页
学科网（北京）股份有限公司1
是BD //平面CMN ，
1 1
因此直线BD 到平面CMN 的距离等于点D 到平面CMN 的距离h，
1 1 1
MN  2,CM CN  CD2DN2  (2 2)212 3 ，
1 1
1 1 1 1 2 17 1 17
V  ( 11)2 ， S   2 32 ( )2  ，V   h ，
CMND 1 3 2 3 CMN 2 2 2 D 1 CMN 3 2
2 17
由V V ，得h ，B错误；
CMND DCMN
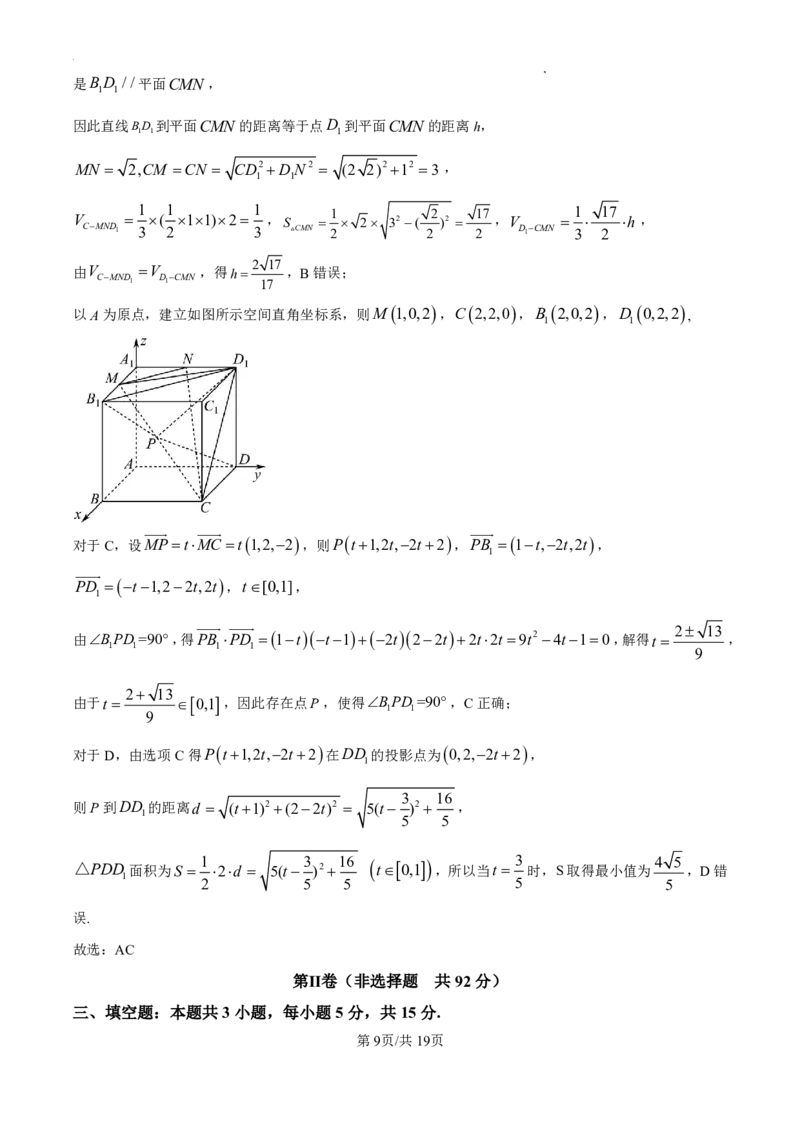
1 1 17
以A为原点，建立如图所示空间直角坐标系，则M  1,0,2  ，C  2,2,0 ，B  2,0,2  ，D  0,2,2  ,
1 1
  
对于C，设MP tMC t  1,2,2 ，则P  t1,2t,2t2  ，PB  1t,2t,2t ，
1

PD
t1,22t,2t ，t[0,1]，
1
由BPD =90，得  P  B    P  D   1t t1 2t  22t 2t2t 9t2 4t10，解得t  2 13 ，
1 1 1 1
9
2 13
由于t   0,1 ，因此存在点P，使得BPD =90，C正确；
1 1
9
对于D，由选项C得P  t1,2t,2t2  在DD 的投影点为  0,2,2t2  ，
1
3 16
则P到DD 的距离d  (t1)2(22t)2  5(t )2 ，
1
5 5
△PDD 面积为S  1 2d  5(t 3 )2 16  t 0,1  ，所以当t  3 时，S取得最小值为 4 5 ，D错
1
2 5 5 5 5
误.
故选：AC
第Ⅱ卷（非选择题 共 92分）
三、填空题：本题共 3小题，每小题 5分，共 15分.
第9页/共19页
学科网（北京）股份有限公司1
12. 若方程x2  y2 4x2y m表示圆，则实数m的取值范围为______________.
【答案】
5,
【解析】
【分析】根据圆的一般方程条件D2 E2 4F 0，计算即可得到答案.
【详解】根据题意，方程x2  y2 4x2ym0表示圆，
则4 2 224 m 0，解得m5.
所以实数m的取值范围为 5, .
故答案为：
5,
.
13. 已知在 中，顶点A  4,2  ，点B在直线l：x y20上，点C在x轴上，则 的周长的最

小值______.
【答案】4 5
【解析】
【分析】设点A关于直线l：x y20的对称点A(x ,y )，点A关于x轴的对称点为A (x ,y )，
1 1 1 2 2 2
连接AA 交l于B，交x轴于C，则此时 的周长取最小值，且最小值为 AA ，利用对称知识求出A
1 2 1 2 1

和A ，再利用两点间距离公式即可求解.
2
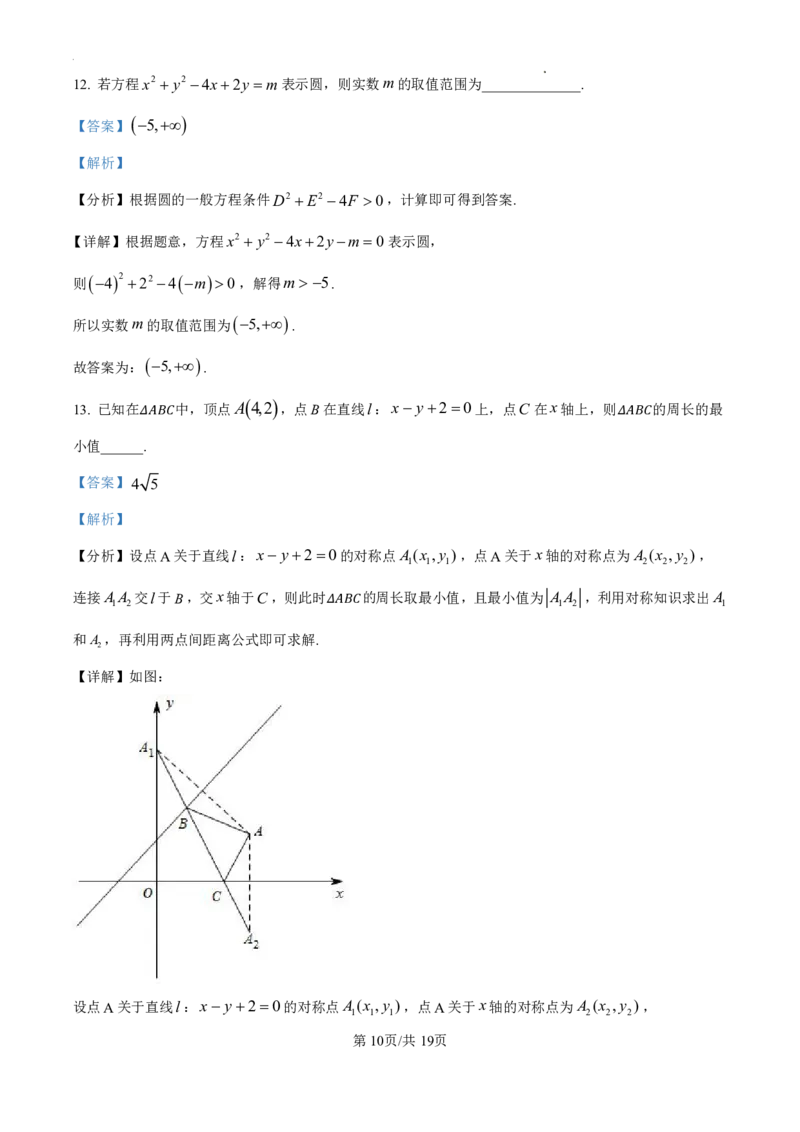
【详解】如图：
设点A关于直线l：x y20的对称点A(x ,y )，点A关于x轴的对称点为A (x ,y )，
1 1 1 2 2 2
第10页/共19页
学科网（北京）股份有限公司1
连接AA 交l于B，交x轴于C，
1 2
则此时 的周长取最小值，且最小值为 AA ，
1 2

 A与A关于直线l：x y20对称，
1
y 2
1 11

x 4 x 0
 1 ，解得： 1 ，
x 4 y 2 y 6
1  1 20 1

2 2
 A(0,6)，易求得：A (4,2)，
1 2
 的周长的最小值 AA  42 (62)2 4 5.
1 2

故答案为：4 5.
【点睛】本题主要考查求一个点关于某直线的对称点的坐标的方法，体现了数形结合的数学思想，综合性
较强.
uur uur uuur
1
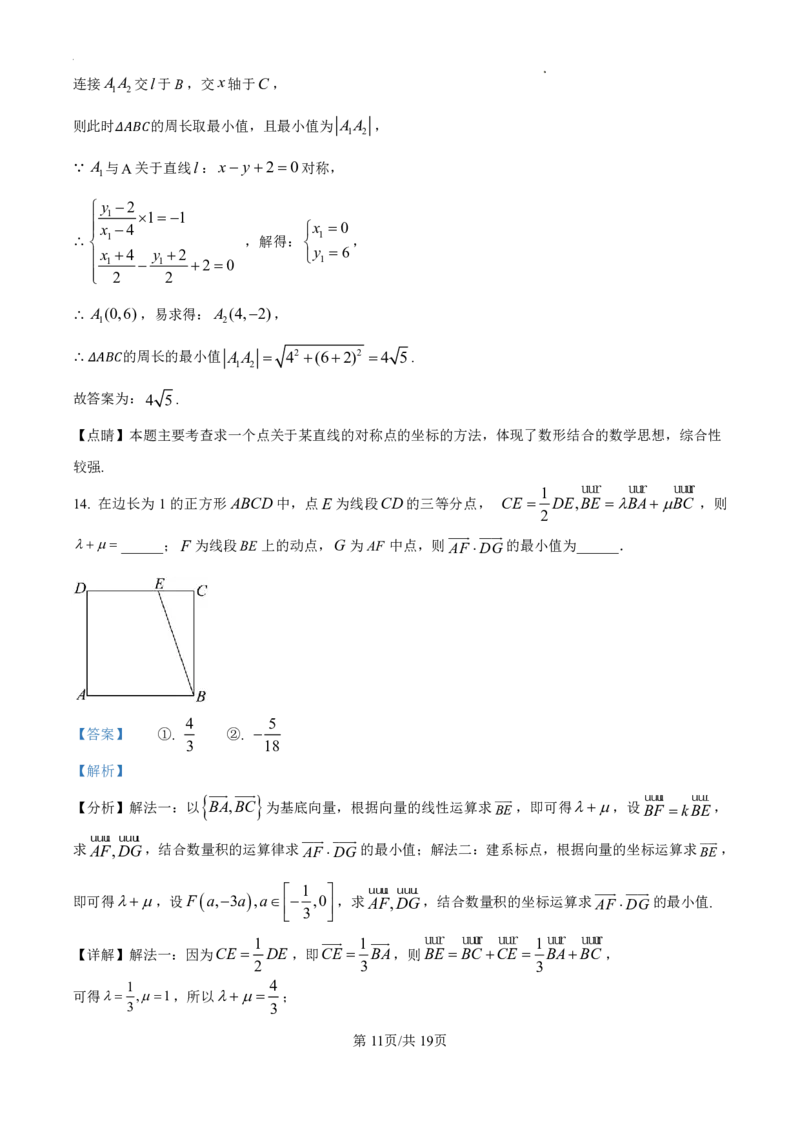
14. 在边长为1的正方形ABCD中，点E为线段CD的三等分点， CE  DE,BE BABC ，则
2
 
______；F 为线段BE 上的动点，G 为AF 中点，则AF DG的最小值为______．
4 5
【答案】 ①. ②. 
3 18
【解析】
  uuur uur
  
【分析】解法一：以 BA,BC 为基底向量，根据向量的线性运算求 BE ，即可得，设 BF kBE ，
uuur uuur
  
求AF,DG，结合数量积的运算律求AF DG的最小值；解法二：建系标点，根据向量的坐标运算求
BE
，
uuur uuur
 1   
即可得，设F  a,3a  ,a

 ,0

，求AF,DG，结合数量积的坐标运算求AF DG的最小值.
 3 
uur uuur uur uur uuur
1  1 1
【详解】解法一：因为CE  DE，即CE  BA，则BE  BCCE  BABC ，
2 3 3
1 4
可得 ,1，所以 ；
3 3
第11页/共19页
学科网（北京）股份有限公司1
   
由题意可知： BC  BA 1,BABC 0，
  1  
因为F 为线段BE 上的动点，设BF kBE  kBAkBC,k 0,1 ，
3
     1  
则AF  ABBF  ABkBE   k1BAkBC ，
3 
    1 11  1 
又因为G为AF 中点，则DG  DA AG BC AF   k1BA  k1BC，
2 23  2 
  1   11  1 
可得AFDG   k 1BAkBC    k 1BA  k 1BC
3   23  2  
2 2
11  1  5 6 3


k1 k k1  k

 ，
23  2  9 5 10
  5
又因为k
0,1

，可知：当k 1时，AF DG取到最小值 ；
18
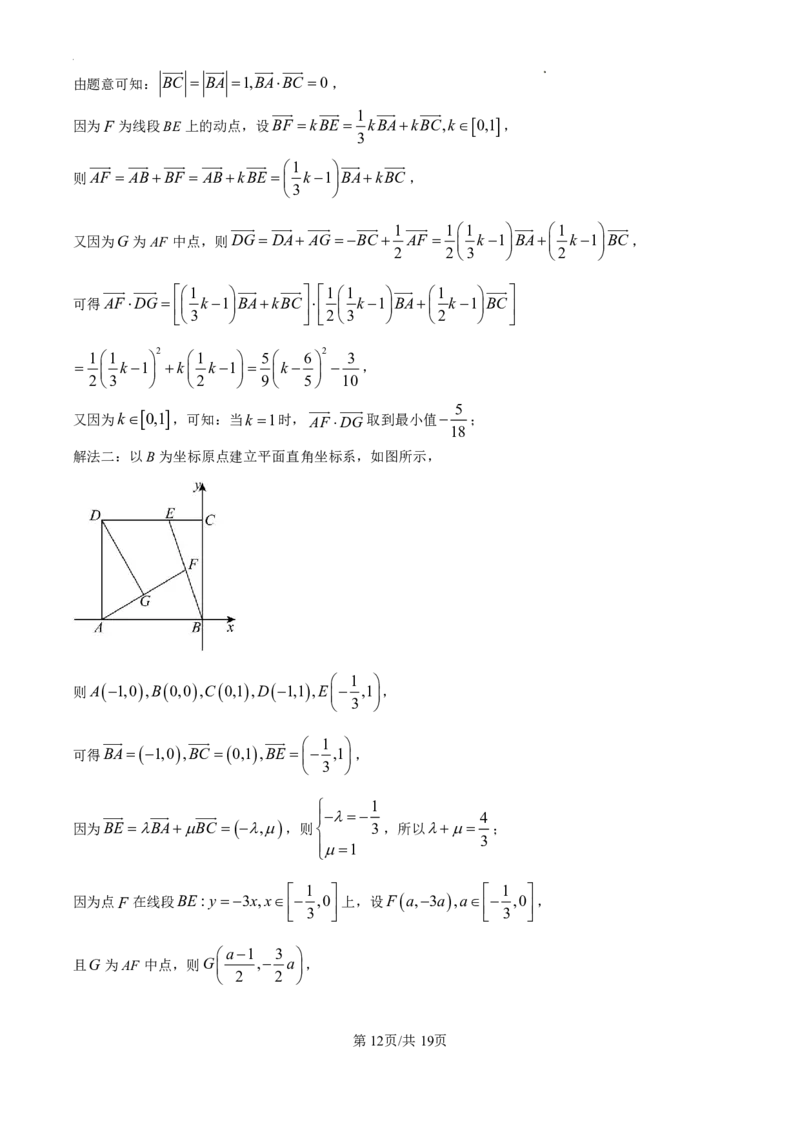
解法二：以B为坐标原点建立平面直角坐标系，如图所示，
 1 
则A 1,0  ,B  0,0  ,C  0,1  ,D 1,1  ,E  ,1，
 3 
    1 
可得BA1,0  ,BC  0,1  ,BE    ,1，
 3 
 1
    4
因为BE BABC  ,，则 3，所以 ；
 1 3
 1   1 
因为点F 在线段BE: y 3x,x

 ,0

上，设F  a,3a  ,a

 ,0

，
 3   3 
a1 3 
且G为AF 中点，则G , a，
 2 2 
第12页/共19页
学科网（北京）股份有限公司1
  a1 3 
可得AF  a1,3a  ,DG   , a1，
 2 2 
   a1 2  3   2 2 3
则AFDG 3a 

 a1 5a

 ，
2  2   5 10
 1  1   5
且a

 ,0

，所以当a 时，AF DG取到最小值为 ；
 3  3 18
4 5
故答案为： ； .
3 18
四、解答题：本题共 5小题，共 77分.解答应写出文字说明、证明过程或演算步骤.
15. 若圆C经过点A1,1和B  1,3  ，且圆心在x轴上，则：
（1）求圆C的方程．
（2）直线 y  x与圆C交于E、F两点，求线段EF 的长度．
【答案】（1）(x2)2  y2 10
（2）4 2
【解析】
【分析】（1）由圆心既在线段AB的垂直平分线上，又在x轴上，可联立直线方程求圆心，进而得半径与圆
的方程；
（2）利用几何法，先求圆心到直线的距离，再利用勾股定理求半弦长即可得.
【小问1详解】
31
因为A 1,1  和B  1,3  ，线段AB的中点为 ，且k  1，
AB 1(1)
0,2
则AB的垂直平分线方程为x y20，由圆的性质可知，圆心在该直线上，
又已知圆心在x轴上，令y0，得x2，
故圆心为C  2,0  ，半径r  CB   21 2  03 2  10，
则圆圆C的方程为(x2)2  y2 10.
【小问2详解】
2
由圆心 到直线x y 0的距离d   2， EF 2 r2 d2 2 102 4 2 .
12 12
2,0
故线段EF 的长度为4 2 .
第13页/共19页
学科网（北京）股份有限公司1
16. 已知三棱柱ABCABC 中，侧棱垂直于底面，点D是AB的中点．
1 1 1
（1）求证：BC //平面CAD；
1 1
（2）若底面ABC为边长为2的正三角形，BB  3，求三棱锥BADC体积．
1 1
【答案】（1）证明见解析
1
（2）
2
【解析】
【分析】（1）连接AC 交AC于点E，连接 ，只要证明DE//BC 即可；
1 1 1

（2）求出CD面AABB，得到 是棱锥的高，利用棱锥的体积公式解答即可.
1 1

【小问1详解】
连接AC 交AC于点E，连接 ，
1 1

四边形AACC是矩形，
1 1
E为AC 的中点，又D是 的中点，
1
第14页/共19页

学科网（北京）股份有限公司1
DE//BC ，又DE 平面CAD,BC 平面CAD,
1 1 1 1
BC // 平面CAD；
1 1
【小问2详解】
AC  BC,D是 的中点，
ABCD，  
又AA 平面ABC,CD平面ABC
1 ,
AA CD,
1
AA AB  A,AA ,AB 平面AABB,
1 1 1 1
CD平面AABB,
1 1
则 是三棱锥CABD的高,
1

1 1 3
又S  BDBB  1 3  ,
A 1 BD 2 1 2 2
1 1 3 1
V V  S AD    3  .
BA 1 DC CA 1 BD 3 A 1 BD 3 2 2
17. 已知V ABC 的三个顶点分别为A2,3，B  0,5 ，C6,1 .
（1）求边AB上的高CD所在直线的方程；
（2）求边AB上的中线CE所在直线的方程.
【答案】（1） y  x7
3 25
（2） y  x
7 7
【解析】
【分析】（1）先求得直线AB的斜率，利用点斜式求得边AB上的高CD所在直线的方程.
（2）先求得E点坐标，再根据两点式求得边AB上的中线CE所在直线的方程.
【小问1详解】
53
k  1，所以直线CD的斜率为1，
AB 02
所以直线CD的方程为 y11 x6  ,y x7
【小问2详解】
第15页/共19页
学科网（北京）股份有限公司1
 
线段AB的中点E 1,4 ，
y1 x6 3 3 25
所以直线CE所在直线方程为  ,y1  x6  ,y  x .
41 16 7 7 7
18. 如图，在棱长4的正方体ABCDABC D 中，E是AA 的中点，点F 在棱CC 上，且CF 1.
1 1 1 1 1 1
（1）求平面ABCD与平面DEF 夹角的余弦值；
（2）若P为平面ABCD内一点，且DP 平面DEF ，求点P到平面DEF 的距离.
1
4 21
【答案】（1）
21
5 21
（2）
21
【解析】
【分析】（1）建立空间直角坐标系，求出平面ABCD和平面DEF 的法向量，求其夹角的余弦值即可得答
案.
（2）利用空间向量的方法解决点到面的距离.
【小问1详解】
以D为坐标原点，DA,DC,DD 所在直线分别为x轴， y 轴，z轴，建立如图所示的空间直角坐标系，
1
第16页/共19页
学科网（北京）股份有限公司1
     
则E 4,0,2 ,F 0,4,1 ,D 0,0,4 ，
1
 
DE  4,0,2  ,DF   0,4,1  .


 nDE  4x2z 0
设平面DEF 的法向量为 ，则  ，

nDF  4yz 0
  =  ,  , 

取 y 1，则x2,z 4，得n  2,1,4  .

因为DD 平面ABCD，所以平面ABCD的一个法向量为DD  0,0,4 ，
1 1


  DD 1 n 4 21
则平面ABCD与平面DEF 夹角的余弦值为 cosDD 1 ,n   D  D  n   21 .
1
【小问2详解】

设P  a,b,0  ，则DP  a,b,4  .
1
因为DP 平面DEF ，所以  D  P  // n  ，则 a  b  4 ，得a 2,b1，即P  2,1,0  .
1 1 2 1 4


 DPn
因为DP  2,1,0 ，所以点P到平面DEF 的距离为   5 21 .
n 21
19. 如图，平面四边形ABCD中，AB8，CD3，AD 5 3，ADC 90，BAD 30，点E，
 2  1
F满足AE  AD，AF  AB，将△AEF 沿EF翻折至!PEF ，使得PC 4 3．
5 2
（1）证明：EF PD；
第17页/共19页
学科网（北京）股份有限公司1
（2）求平面PCD与平面PBF所成的二面角的正弦值．
【答案】（1）证明见解析
8 65
（2）
65
【解析】
【分析】（1）由题意，根据余弦定理求得 EF 2 ，利用勾股定理的逆定理可证得 EF AD ，则
EF PE,EF DE ，结合线面垂直的判定定理与性质即可证明；
（2）由（1），根据线面垂直的判定定理与性质可证明PE  ED，建立如图空间直角坐标系E xyz ，利
用空间向量法求解面面角即可.
【小问1详解】
 2  1
由AB8,AD5 3,AE  AD,AF  AB ，
5 2
得AE 2 3,AF 4，又BAD30，在△AEF 中，
由余弦定理得 EF  AE2AF22AEAFcosBAD  1612242 3 3  2 ,
2
所以AE2 EF2  AF2，则AE EF ，即EF AD，
所以EF PE,EF DE ，又PEDE E,PE、DE  平面PDE，
所以EF 平面PDE，又PD 平面PDE，
故EF  PD；
【小问2详解】
连接CE，由ADC90,ED3 3,CD3，则CE2 ED2CD2 36，
在PEC中，PC 4 3,PE 2 3,EC 6，得EC2 PE2  PC2，
所以PE EC，由（1）知PE  EF ，又ECEF E,EC、EF  平面ABCD，
所以PE 平面ABCD，又ED平面ABCD，
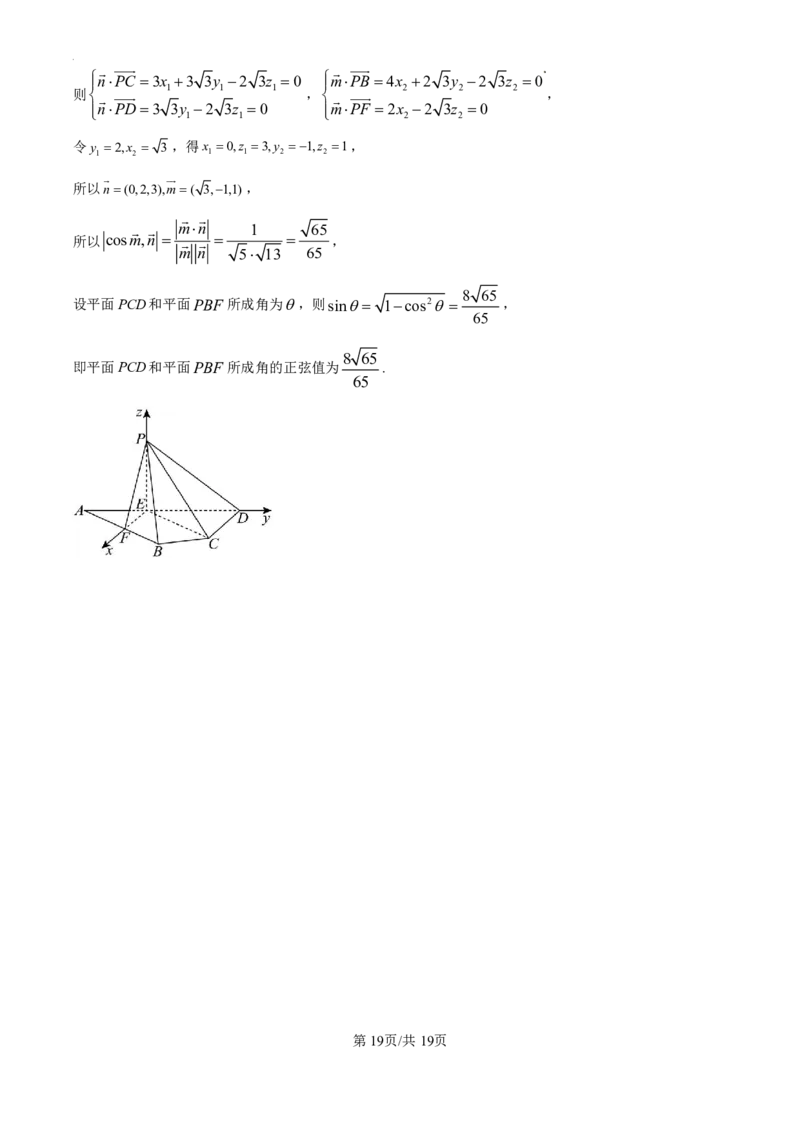
所以PE  ED，则PE,EF,ED 两两垂直，建立如图空间直角坐标系E xyz，
则E(0,0,0),P(0,0,2 3),D(0,3 3,0),C(3,3 3,0),F(2,0,0),A(0,2 3,0)，
由F 是AB的中点，得B(4,2 3,0)，
   
所以PC (3,3 3,2 3),PD(0,3 3,2 3),PB(4,2 3,2 3),PF (2,0,2 3) ，
 
设平面PCD和平面PBF 的一个法向量分别为n(x ,y ,z ),m(x ,y ,z )，
1 1 1 2 2 2
第18页/共19页
学科网（北京）股份有限公司1  
 
 nPC 3x 3 3y 2 3z 0  mPB 4x 2 3y 2 3z 0
则  1 1 1 ，  2 2 2 ，
 
nPD3 3y 2 3z 0 mPF 2x 2 3z 0
1 1 2 2
令y 2,x  3，得x 0,z 3,y 1,z 1，
1 2 1 1 2 2
 
所以n(0,2,3),m( 3,1,1) ，
 
  mn 1 65
所以 cosm,n      ，
m n 5 13 65
8 65
设平面PCD和平面PBF 所成角为，则sin 1cos2 ，
65
8 65
即平面PCD和平面PBF 所成角的正弦值为 .
65
第19页/共19页
学科网（北京）股份有限公司