文档内容
石嘴山市第一中学2024-2025学年高二年级9月月考 7.已知点 是椭圆 上的动点,过 作圆 的两条切线分别为切于点 ,直线
数学试题
与 轴分别相交于 两点,则 ( 为坐标原点)的最小面积为( )
A. B. C. D.
一、单选题
1.已知集合 ,则 ( )
二、多选题
8.下列命题中正确的是( )
A. B. C. D.
A.若 ,则
2.已知复数 满足 ,其中 为虚数单位,则 在复平面内对应的点在( )
B.若 ,则
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.与直线 平行且过点 的直线方程是( ) C.若 ,则
D.若 ,则
A.
9.下列说法正确的有( )
B.
A.不等式 的解集是
C.
B.“ ”是“ ”成立的充分条件
D.
C.命题 ,则
4.圆x2+y2-2x+4y+3=0的圆心到直线x-y=1的距离为( )
D.“ ”是“ ”的必要条件
A.2 B. C.1 D.
10.已知正方形ABCD在平面直角坐标系xOy中,且AC: ,则直线AB的方程可能为( )
5.若直线 与直线 的交点位于第一象限,则直线l的倾斜角的取值范围是( )
A. B.
C. D.
A. B.
11.下列结论正确的是( )
C. D.
A.已知点 在圆 上,则 的最大值是4
B.已知直线 和以 为端点的线段相交,则实数 的取值范围为
6.若圆 上恰有三点到直线 的距离为2,则 的值为( )
C.已知 是圆 外一点,直线 的方程是 ,则直线 与圆相离
A. B. C. D.2
第11页 共24页 ◎ 第12页 共24页
学科网(北京)股份有限公司为坐标原点.
D.若圆 上恰有两点到点 的距离为1,则 的取值范围是
(1)求 的轨迹方程;
(2)当 时,求 的方程及 的面积.
三、填空题
12.圆心在直线y=x上且与x轴相切于点 的圆的方程是 .
18.如图,在四棱锥 中, , , ,点 在 上,且 ,
.
13.若三点 , , ,( )共线,则 的值等于 .
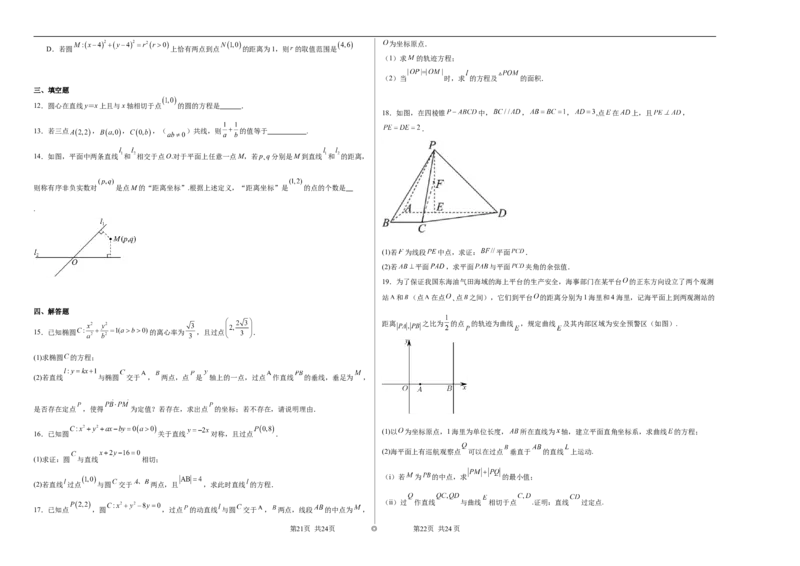
14.如图,平面中两条直线 和 相交于点O.对于平面上任意一点M,若p、q分别是M到直线 和 的距离,
则称有序非负实数对 是点M的“距离坐标”.根据上述定义,“距离坐标”是 的点的个数是
.
(1)若 为线段 中点,求证: 平面 .
(2)若 平面 ,求平面 与平面 夹角的余弦值.
19.为了保证我国东海油气田海域的海上平台的生产安全,海事部门在某平台 的正东方向设立了两个观测
站 和 (点 在点 、点 之间),它们到平台 的距离分别为1海里和4海里,记海平面上到两观测站的
四、解答题
距离 之比为 的点 的轨迹为曲线 ,规定曲线 及其内部区域为安全预警区(如图).
15.已知椭圆 的离心率为 ,且过点 .
(1)求椭圆 的方程;
(2)若直线 与椭圆 交于 , 两点,点 是 轴上的一点,过点 作直线 的垂线,垂足为 ,
是否存在定点 ,使得 为定值?若存在,求出点 的坐标;若不存在,请说明理由.
(1)以 为坐标原点,1海里为单位长度, 所在直线为 轴,建立平面直角坐标系,求曲线 的方程;
16.已知圆 关于直线 对称,且过点 .
(2)海平面上有巡航观察点 可以在过点 垂直于 的直线 上运动.
(1)求证:圆 与直线 相切;
(i)若 为 的中点,求 的最小值;
(2)若直线 过点 与圆 交于 两点,且 ,求此时直线 的方程.
(ii)过 作直线 与曲线 相切于点 .证明:直线 过定点.
17.已知点 ,圆 ,过点 的动直线 与圆 交于 , 两点,线段 的中点为 ,
第21页 共24页 ◎ 第22页 共24页第31页 共24页 ◎ 第32页 共24页
学科网(北京)股份有限公司