天津市南开区2024-2025学年高三上学期11月期中考试数学PDF版含答案_2024-2025高三（6-6月题库）_2024年11月试卷_1117天津市南开区2024-2025学年高三上学期11月期中考试

{#{QQABSYCAoggoQBJAAQhCAQFiCgCQkhEAAQgOwBAEIAAByQNABAA=}#}{#{QQABSYCAoggoQBJAAQhCAQFiCgCQkhEAAQgOwBAEIAAByQNABAA=}#}{#{QQABSYCAoggoQBJAAQhCAQFiCgCQkhEAAQgOwBAEIAAByQNABAA=}#}{#{QQABSYCAoggoQBJAAQhCAQFiCgCQkhEAAQgOwBAEIAAByQNABAA=}#}{#{QQABSYCAoggoQBJAAQhCAQFiCgCQkhEAAQgOwBAEIAAByQNABAA=}#}{#{QQABSYCAoggoQBJAAQhCAQFiCgCQkhEAAQgOwBAEIAAByQNABAA=}#}{#{QQABSYCAoggoQBJAAQhCAQFiCgCQkhEAAQgOwBAEIAAByQNABAA=}#}{#{QQABSYCAoggoQBJAAQhCAQFiCgCQkhEAAQgOwBAEIAAByQNABAA=}#}2024—2025 学年度第一学期阶段性质量监测（一）参考答案 高三年级 数学学科 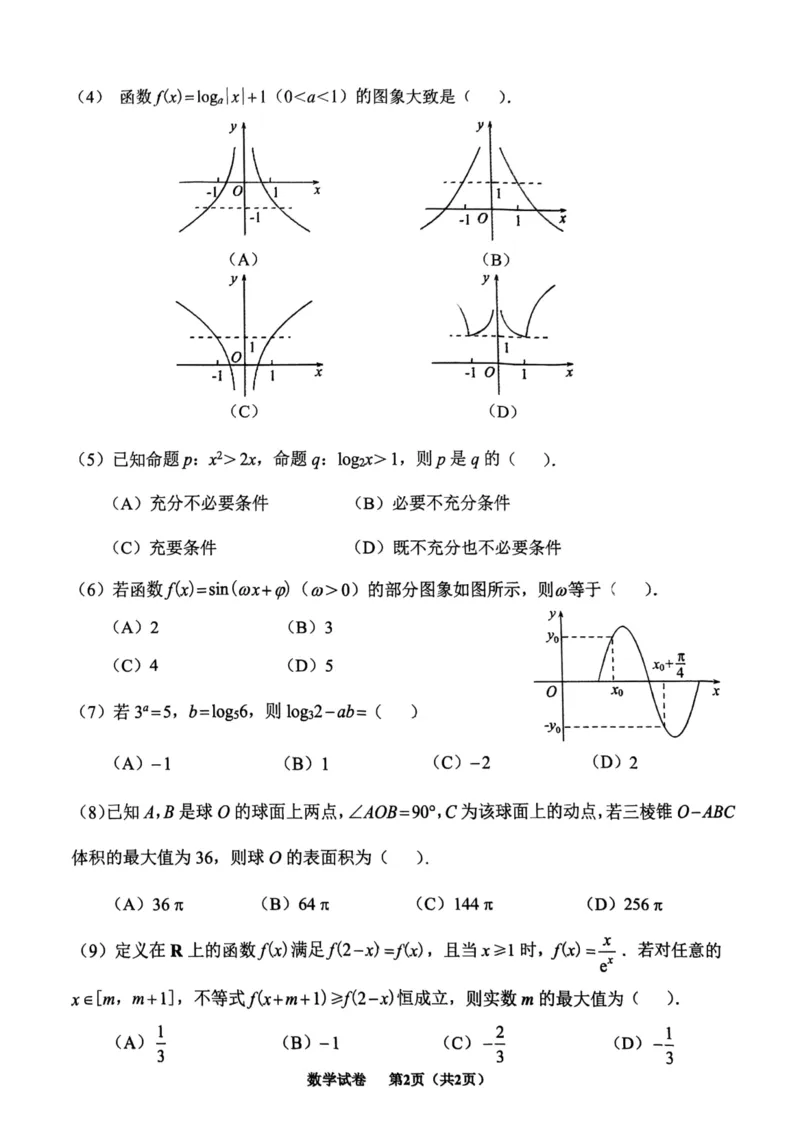一、选择题：（本题共9小题，每题5分，共45分） 题 号 （1） （2） （3） （4） （5） （6） （7） （8） （9） 答 案 D C A B B C A C D 二、填空题：（本题共6小题，每题5分，共30分） （10）−1； （11）−4； （12） 数学试卷参考答案 第1页（共6页）  0 ， 1 3  ； （13） − 3 + 1 4 0 3 （14）a + 3 4 b， 2 1 2 ； （15）−1或2，  1 + 3 ， 1 9 5  ． 三、解答题：（其他正确解法请比照给分） （16）解：（Ⅰ）f(x)=2cos(2x+ π 3 )+1，令 − π + 2 k π ≤ 2 x + π 3 ≤ 2 k π ，kZ， 2 π 解得− π+kπ≤x≤− +kπ，kZ， 3 6 所以函数的单调递增区间为  − 2 3 π + k π ， − π 6 + k π  ，kZ． ………………4分 （Ⅱ）因为  0 ， π 2  ，所以2x+ π 3  4π  ， ， ………………6分   3 3  可得cos(2x+ π 3 )  − 1 ， 1 2  ， ………………10分 π 则2cos(2x+ )+1[−1，2]， 3 即函数f(x)在  0 ， π 2  上的值域为[−1，2]． ………………14分 b2 +c2 −a2 bc 1 （17）解：（Ⅰ）由b2+c2=a2+bc，得cosA= = = ， ………………2分 2bc 2bc 2 π 由A(0，)，所以A= ． ………………4分 3 （Ⅱ）（ⅰ）因为sinC=3sinB，所以由正弦定理得c=3b， ① ………………5分 {#{QQABSYCAoggoQBJAAQhCAQFiCgCQkhEAAQgOwBAEIAAByQNABAA=}#}又b2+c2=4+bc，② 联立①②解得 数学试卷参考答案 第2页（共6页） b = 2 7 7 ， c = 6 7 7 ． ………………7分 （ⅱ）由（ⅰ）知 c o s B = a 2 + 2 c a 2 c − b 2 = 4 2 +  2 3 6 7 6  − 7 4 77 = 5 1 4 7 ． ………………8分 从而sinB = 1 2 4 1 ， ………………9分 所以cos2B=2cos2B−1= 1 1 1 4 ，sin2B=2sinBcosB= 5 1 4 3 ， ………………11分 所以cos(A−2B)= cos( π 3 −2B) ………………12分 = cos π 3 cos 2B + sin π 3 sin2B ………………13分 = 1 2  1 1 1 4 + 2 3 5 3  = 14 1 1 3 4 ． ………………15分 （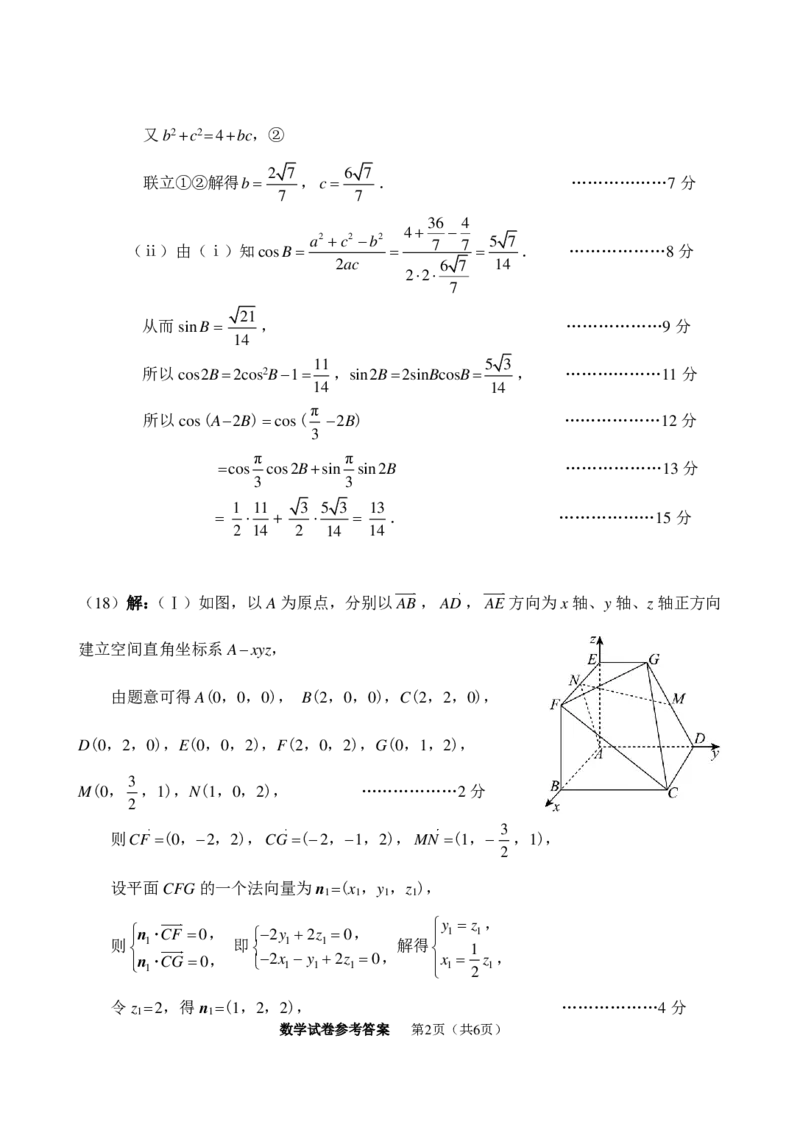18）解：（Ⅰ）如图，以A为原点，分别以 A B ， A D ， A E 方向为x轴、y轴、z轴正方向 建立空间直角坐标系A−xyz， 由题意可得A(0，0，0)， B(2，0，0)，C(2，2，0)， D(0，2，0)，E(0，0，2)，F(2，0，2)，G(0，1，2)， M(0， 3 2 ，1)，N(1，0，2)， ………………2分 则CF =(0，−2，2)，CG =(−2，−1，2)， M N 3 =(1，− ，1)， 2 设平面CFG的一个法向量为n =(x ，y ，z )， 1 1 1 1  n  CF =0 ， −2y +2z =0 ，   y 1 =z 1 ， 则 1 即 1 1 解得 1 n 1  CG=0 ， −2x 1 −y 1 +2z 1 =0 ，   x 1 = 2 z 1 ， 令z =2，得n =(1，2，2)， ………………4分 1 1 {#{QQABSYCAoggoQBJAAQhCAQFiCgCQkhEAAQgOwBAEIAAByQNABAA=}#}3 所以n • MN =(1，2，2) • (1，− ，1) =0， ………………5分 1 2 所以MN ⊥n ，又MN平面CFG， ………………6分 1 所以MN∥平面CFG． ………………7分 （Ⅱ）由（Ⅰ）得直线AN的一个方向向量为 数学试卷参考答案 第3页（共6页） A N =(1，0，2)，平面CFG的一个法向量 为n =(1，2，2)， 1 设直线AN与平面CFG所成角为， 则sin=|cos|= | | n n 1 1|  | A N A N | | = 1 1 2  + 1 2 + 2 0   1 2 2 + + 2 2  2 2 + 2 2 = 3 5 5 = 5 3 ， 所以直线AN与平面CFG所成角的正弦值为 3 5 ． ………………10分 （Ⅲ）设平面CDG的一个法向量n =(x ，y ，z )， 2 2 2 2 由（Ⅰ）可得 C D =(−2，0，0)， C G =(−2，−1，2)，  n  CD=0 ， 则 2 即 n 2  CG=0 ，  − − 2 2 x x 2 2 = − 0 y ， 2 + 2 z 2 = 0 ， 解得  x y 2 2 = = 0 2 ， z 2 ， 令z =1，得n =(0，2，1)， ………………12分 2 2 设平面POB与平面PAB的夹角为， |n  n | 01+22+12 6 2 5 则cos=|cos|= 1 2 = = = ， 1 2 |n 1 ||n 2 | 22 +12 12 +22 +22 53 5 2 5 所以平面CDG与平面CFG夹角的余弦值为 ． ………………15分 5 a （19）解：（Ⅰ）由已知得f(x)=ex− ， ………………1分 x+1 则f(0)=e0−a=1−a，又f(0)=1， ………………3分 {#{QQABSYCAoggoQBJAAQhCAQFiCgCQkhEAAQgOwBAEIAAByQNABAA=}#}所以f(x)图象在点(0，f(0))处的切线方程为y=(1−a)x+1， 将点(2，1)代入得1=2(1−a)+1，解得a=1． ………………6分 （Ⅱ）所以f(x)=ex−ln(x+1)，定义域为(−1，+∞)， ………………7分 所以f(x)=ex− 数学试卷参考答案 第4页（共6页） x 1 + 1 = ( x + 1 x ) + e x 1 − 1 ， 令g(x)=(x+1)ex−1（x＞−1），则g(x)=(x+2)ex， 易得g(x)＞0在(−1，+∞)上恒成立，所以g(x)在(−1，+∞)上单调递增， ………………10分 又g(0)=0， ………………11分 所以当−1＜x＜0时，g(x)＜0，即f(x)＜0，f(x)在(−1，0)上单调递减， 当x＞0时，g(x)＞0，即f(x)＞0，f(x)在(0，+∞)上单调递增， 所以f(x)在x=0处取得极小值，极小值为f(0)=1，无极大值． ………………15分 （20）解：（Ⅰ）当a = 1时，f(x)= ex − 1 + lnx + 2 x ，定义域为(0，+∞)， 1 则f (x)= ex − 1 + − x 2 2 x = 1 x  x e x − 1 + 1 − 2 x  ， 令g(x)= xex − 1 + 1 − 2 x ，x＞0， 则g (x)= (x + 1)ex − 1 + 2 2 x ＞0，所以g(x)在(0，+∞)单调递增， 其中g(1)=e0+1−2=0， 故当0＜x＜1时，g(x)＜0，即f(x)＜0，f(x)单调递减； 当x＞1时，g(x)＞0，即f(x)＞0，f(x)单调递增； {#{QQABSYCAoggoQBJAAQhCAQFiCgCQkhEAAQgOwBAEIAAByQNABAA=}#}f(x)在x = 1处取最小值，又f(1)= e1 − 1 + ln1 + 数学试卷参考答案 第5页（共6页） 2 1 =3， 故f(x)的最小值为3． ………………6分 （Ⅱ）由（Ⅰ）知，当a=1时，f(x) =3，即f(x)≥3成立； ………………7分 min 下面证明当0＜a＜1时，f(x)≥3也成立． 因为f(x)= aex − 1 + lnx + 2 a x ，定义域为(0，+∞)， 1 所以f (x)= aex − 1 + − x a 2 x 2 = 1 x  a x e x − 1 + 1 − 2 a x  ， 2 令h(x)= axex − 1 + 1 − ，又0 ＜ a ＜ 1， ax 2 则h(x)= a(x + 1)ex − 1 + ax2 ＞ 0，所以h(x)在区间(0，+∞)单调递增， 其中h(1)=a+1− 2 a = ( a + 2 ) a ( a − 1 ) ＜0，且 h  1 a  = e 1a − 1 − 1 ＞0， 由零点存在性定理及单调性可知，存在唯一实数x (1， 0 1 a )， 使h(x )= 0 a x 0 e x0 − 1 + 1 − a 2 x 0 = 0 ，即f(x )=0，则 0 a e x0 − 1 = a 2 x 20 − 1 x 0 ，① 当x(0，x )时，h(x)＜0，f(x)＜0，f(x)单调递减； 0 当x(x ，+∞)时，h(x)＞0，f(x)＞0，f(x)单调递增； 0 所以f(x) =f(x )= min 0 a e x0 − 1 + ln x 0 + a 2 x 0 ，将①式代入可得， 2 1 2 f(x )= − +lnx + ，② ………………11分 0 ax2 x 0 ax 0 0 0 下面先证 ln x 0  1 − 1 x 0 1 ，x (1， )， 0 a 1 令(x)= lnx+ ，x(1，+∞)， x 1 1 x−1 则(x)= − = 0，(x)在(1，+∞)单调递增， x x2 x2 {#{QQABSYCAoggoQBJAAQhCAQFiCgCQkhEAAQgOwBAEIAAByQNABAA=}#}则(x)＞(1)=1，即 数学试卷参考答案 第6页（共6页） ln x  1 − 1 x ，故当x (1， 0 1 a )， ln x 0  1 − 1 x 0 ．③ 由②③式可得， f(x )= 0 a 2 x 20 − 1 x 0 + ln x 0 + a 2 x 0 ＞ a 2 x 20 − 2 x 0 + a 2 x 0 + 1 = 2 [ 1 + ( 1 a − 2 x 0 a ) x 0 ] + 1 ， 1 又因为1＜x ＜ ，则ax 2−[(1−a)x +]=(ax −1)(x +)＜0， 0 0 0 0 0 a 即(1−a)x +＞ax 2＞0， 0 0 所以 2 [ 1 + ( 1 a − 2 x 0 a ) x 0 ] + 1 ＞2+=3，所以f(x )＞3，则有f(x)≥f(x) =f(x )＞3． 0 min 0 故当0＜a＜1时，f(x)≥3也成立． ………………15分 综上所述，当0＜a≤1时，f(x)≥3． ………………16分 {#{QQABSYCAoggoQBJAAQhCAQFiCgCQkhEAAQgOwBAEIAAByQNABAA=}#}