期中考试卷_2024-2025高二（7-7月题库）_2024年11月试卷_1123云南省玉溪市一中2024-2025学年高二上学期期中考试_云南省玉溪市一中2024-2025学年高二上学期期中考试数学试题PDF版含答案

玉溪一中 2024—2025 学年上学期高二年级期中考 数学学科试卷 总分：150分，考试时间：120分钟 命题人：任红波 夏荣 谢娇艳 审题人：古莹莹 一．选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有 一项是符合题目要求的．  1.若直线l的一个方向向量n(1, 3)，则l的倾斜角为（ ） A. 30 B. 60 C. 120 D. 150 2.已知直线l :2xmy1，l :mx8ym2，则“m4”是“l //l ”的（ ） 1 2 1 2 A.充分不必要条件 B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件 3.与直线3x4y50关于x轴对称的直线方程为（ ） A.3x4y50 B.4x3y50 C.4x3y50 D.3x4y50 4.圆x2  y2 6x0和圆x2  y2 4x6y 0的公共弦长为（ ） 9 10 9 10 7 10 7 10 A. B. C. D. 5 10 5 10 5.椭圆x2 my2 1的焦点在y轴上，长轴长是短轴长的两倍，则m的值为（ ） 1 1 A. B. C. 2 D. 4 2 4 6．若圆C:(x1)2(y3)2 8上存在四个点到直线l:x ym0的距离为 2，则实数m 的取值范围是（ ） A．10m2 B．6m2 C．2m2或10m6 D．m6或m2 x2 y2 7．点F为椭圆C：  1ab0的右焦点，直线l：ykx与椭圆C交于A，B两 a2 b2 点，O为坐标原点，△OAF 为正三角形，则椭圆的离心率为（ ） 31 31 A． 31 B．2 3 C． D． 2 2 2 8．如图，正方体ABCDABCD 的棱长为1，线段BD上有两个动点E,F，且EF  ．则 1 1 1 1 1 1 2 下列结论中错误的是（ ） A．三棱锥ABEF 的体积为定值 第 1 页 试卷共 4 页B．当E向D 运动时，二面角AEF B的大小不变 1 C．二面角EABC的最小值为45 D．当E向D 运动时，AECF 总成立 1 二．选择题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符 合题目要求．全部选对的得6分，部分选对的得部分分，有选错的得0分． 9.下列说法中正确的是（ ）    A．已知AB(4,2,6)，AC(2,8,4)，AD(3,5,)，若A，B，C，D四点共面，则实 数为5 B．若直线l的一个方向向量与平面的一个法向量的夹角等于120，则直线l与平面所 成的角等于 60   C．已知点 A(1,2,1)，B(3,3,2)，C(1,4,3)，若 AB ， AC 的夹角为锐角，则的取值 范围为(2,4)(4,)   D．已知直线l的一个方向向量是n(4,2,3)，平面的一个法向量是m  (1,2,0)，则 l // 10．已知椭圆 x2  y2 1的左，右焦点为F，F ，A，B分别为它的左右顶点，点P为椭圆 1 2 16 9 上的动点（P不在x轴上），下列选项正确的是（ ）  A．存在点P使得FPF  B．PFF 的周长为 82 7 1 2 2 1 2 9 1 1 1 C．直线PA与直线PB的斜率乘积为 D．  的最小值为 16 PF PF 2 1 2 11.已知圆C的方程为x2 (y1)2 2，则下列结论正确的是（ ） A. 若P(x,y)为圆C上的点，则 （x2）2 （y1）2 的最大值为 3 2 B. 已知直线l:(m1)xmy12m0与圆C所截得的弦长最短，则m的值为0 C. 由直线l:x y30上的一点向圆C引切线，则切线长的最小值为 2 2 D. 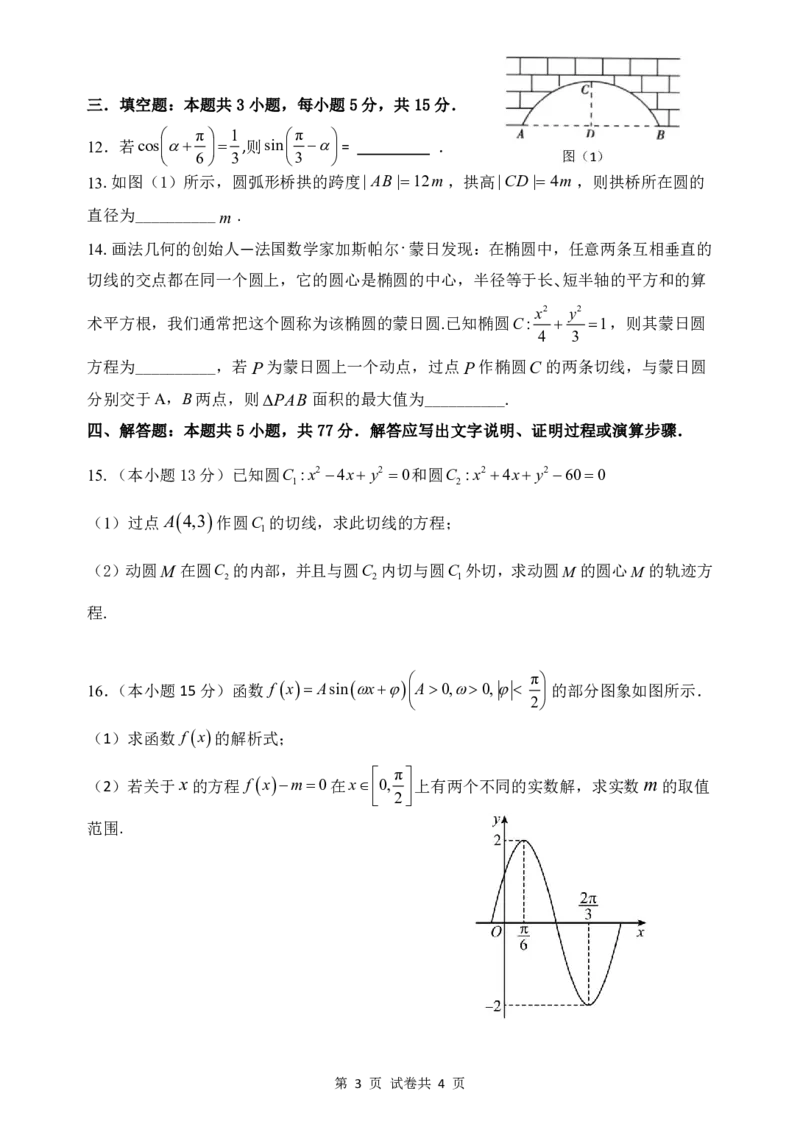若圆C上任一点P(x,y)，其坐标均使得不等式x ym 0恒成立，则实数m的取值 范围是[1,) 第 2 页 试卷共 4 页三．填空题：本题共3小题，每小题5分，共15分．  π 1 π  12．若cos  ,则sin = ．  6 3 3  图（1） 13.如图（1）所示，圆弧形桥拱的跨度| AB|12m，拱高|CD| 4m，则拱桥所在圆的 直径为__________m . 14.画法几何的创始人—法国数学家加斯帕尔蒙日发现：在椭圆中，任意两条互相垂直的 切线的交点都在同一个圆上，它的圆心是椭圆的中心，半径等于长､短半轴的平方和的算 x2 y2 术平方根，我们通常把这个圆称为该椭圆的蒙日圆.已知椭圆C:  1，则其蒙日圆 4 3 方程为__________，若P为蒙日圆上一个动点，过点P作椭圆C的两条切线，与蒙日圆 分别交于A，B两点，则PAB 面积的最大值为__________. 四、解答题：本题共5小题，共77分．解答应写出文字说明、证明过程或演算步骤． 15.（本小题13分）已知圆C :x24x y2 0和圆C :x24x y2600 1 2   （1）过点A 4,3 作圆C 的切线，求此切线的方程； 1 （2）动圆M 在圆C 的内部，并且与圆C 内切与圆C 外切，求动圆M的圆心M 的轨迹方 2 2 1 程. 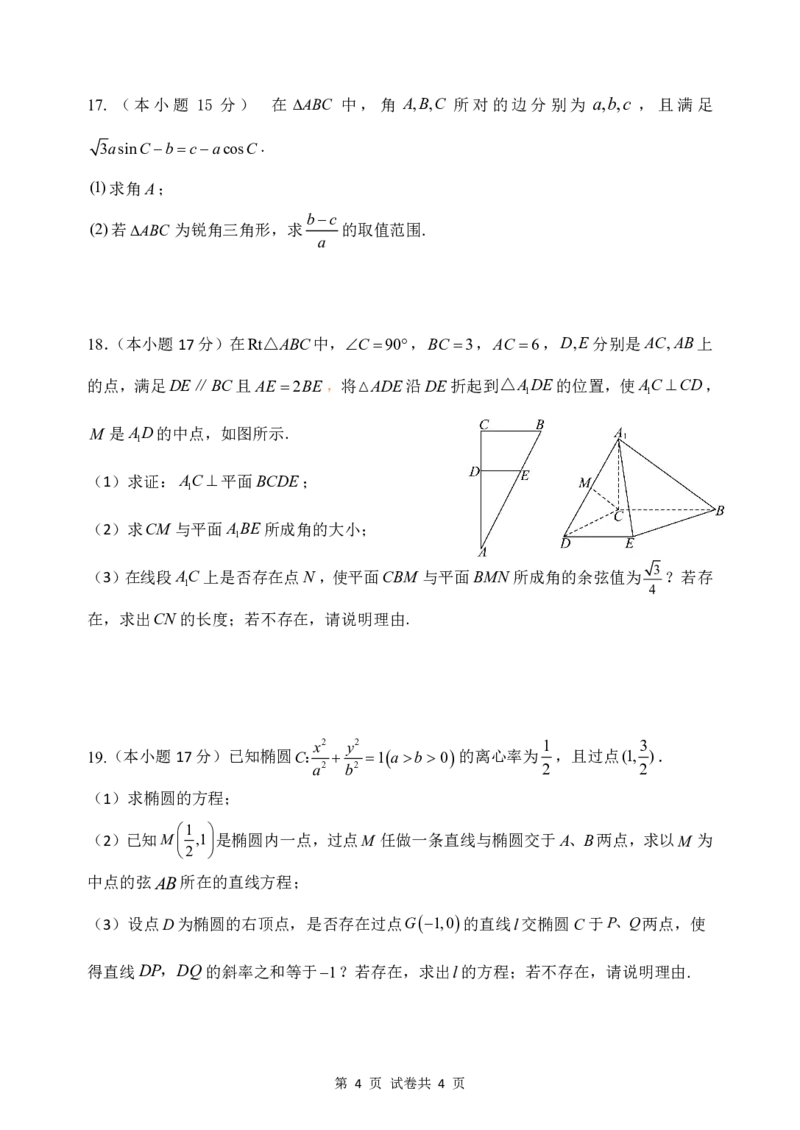 π 16．（本小题15分）函数 f xAsinx A0,0,  的部分图象如图所示．  2 （1）求函数 f x的解析式；  π （2）若关于x的方程 f xm0在x  0,  上有两个不同的实数解，求实数m的取值  2 范围. 第 3 页 试卷共 4 页17.（本小题 15 分） 在 ABC 中，角 A,B,C 所对的边分别为 a,b,c ，且满足 3asinCbcacosC. (1)求角A； bc (2)若ABC 为锐角三角形，求 的取值范围. a 18．（本小题17分）在Rt△ABC中，C90，BC3，AC6，D,E分别是AC,AB上 的点，满足DE∥BC且AE2BE，将VADE沿DE折起到△ADE的位置，使ACCD， 1 1 M 是AD的中点，如图所示. 1 （1）求证：AC平面BCDE； 1 （2）求CM 与平面ABE所成角的大小； 1 3 （3）在线段AC上是否存在点N ，使平面CBM 与平面BMN所成角的余弦值为 ？若存 1 4 在，求出CN 的长度；若不存在，请说明理由. x2 y2 1 3 19.（本小题17分）已知椭圆C：  1a b0的离心率为 ，且过点(1, )． a2 b2 2 2 （1）求椭圆的方程； 1  （2）已知M ,1是椭圆内一点，过点M 任做一条直线与椭圆交于A、B两点，求以M 为 2  中点的弦AB所在的直线方程； （3）设点D为椭圆的右顶点，是否存在过点G1,0的直线l交椭圆C于P、Q两点，使 得直线DP，DQ的斜率之和等于1？若存在，求出l的方程；若不存在，请说明理由. 第 4 页 试卷共 4 页