2003年北京高考文科数学真题及答案_数学高考真题试卷_旧1990-2007·高考数学真题_1990-2007·高考数学真题·PDF_北京

2003 年北京高考文科数学真题及答案 本试卷分第Ⅰ卷（选择题）第Ⅱ卷（非选择题）两部分，共150分，考试时间120分钟 第Ⅰ卷（选择题 共50分） 注意事项： 1．答第Ⅰ卷前，考生务必将自己姓名、准考证号、考试科目用铅笔涂写在答题卡上. 2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡 皮擦干净后，再选涂其它答案，不能答在试题卷上. 3．考试结束，监考人将本试卷和答题卡一并收回. 参考公式： 三角函数的积化和差公式： 正棱台、圆台的侧面积公式 1 1 sincos [sin()sin()] S  (cc)l 2 台侧 2 1 cossin [sin()sin()] 其中c、c分别表示上、下底面 2 1 coscos [cos()cos()] 周长，l表示斜高或母线长. 2 1 sinsin  [cos()cos()] 球 体 的 体 积 公 式 ： 2 4 V  R3，其中R表示球的半径. 球 3 一、选择题：本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有 一项是符合要求的. 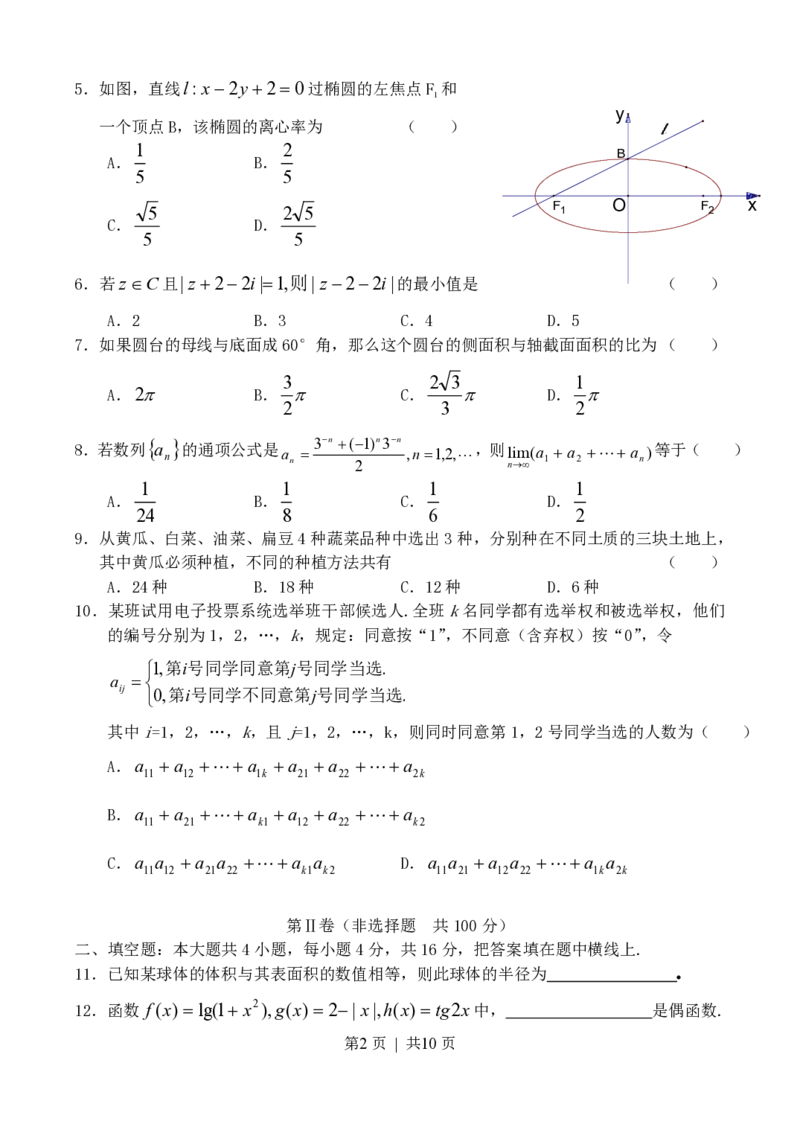1．设集合A{x| x2 10},B {x|log x 0|},则AB等于 （ ） 2 A．{x|x1} B．{x| x 0} C．{x|x1} D．{x| x  1或x 1} 1 2．设y  40.9,y 80.44,y ( )1.5，则 （ ） 1 2 3 2 A．y>y>y B．y>y>y C．y>y>y D．y>y>y 3 1 2 2 1 3 1 2 3 1 3 2 3 5 3．“cos2 ”是“2k ,kZ ”的 （ ） 2 12 A．必要非充分条件 B．充分非必要条件 C．充分必要条件 D．既非充分又非必要条件 4．已知α，β是平面，m，n是直线.下列命题中不正确的是 （ ） A．若m∥α，α∩β=n，则m//n B．若m∥n，α∩β=n，则n⊥α C．若m⊥α，m⊥β，则α∥β D．若m⊥α，m，则α⊥β 第1页 | 共10页5．如图，直线l:x2y20过椭圆的左焦点F 和 1 y 一个顶点B，该椭圆的离心率为 （ ） 1 2 B A． B． 5 5 F O F x 5 2 5 1 2 C． D． 5 5 6．若zC且| z22i|1,则| z22i|的最小值是 （ ） A．2 B．3 C．4 D．5 7．如果圆台的母线与底面成60°角，那么这个圆台的侧面积与轴截面面积的比为（ ） 3 2 3 1 A．2 B．  C．  D．  2 3 2 8．若数列  a n  的通项公式是 a n  3n ( 2 1)n3n ,n1,2,  ，则 n li  m  (a 1 a 2   a n )等于（ ） 1 1 1 1 A． B． C． D． 24 8 6 2 9．从黄瓜、白菜、油菜、扁豆4种蔬菜品种中选出3种，分别种在不同土质的三块土地上， 其中黄瓜必须种植，不同的种植方法共有 （ ） A．24种 B．18种 C．12种 D．6种 10．某班试用电子投票系统选举班干部候选人.全班k名同学都有选举权和被选举权，他们 的编号分别为1，2，…，k，规定：同意按“1”，不同意（含弃权）按“0”，令 1,第i号同学同意第j号同学当选. a  ij 0,第i号同学不同意第j号同学当选. 其中i=1，2，…，k，且j=1，2，…，k，则同时同意第1，2号同学当选的人数为（ ） A．a a  a a a  a 11 12  1k 21 22  2k B．a a  a a a  a 11 21  k1 12 22  k2 C．a a a a  a a D．a a a a  a a 11 12 21 22  k1 k2 11 21 12 22  1k 2k 第Ⅱ卷（非选择题 共100分） 二、填空题：本大题共4小题，每小题4分，共16分，把答案填在题中横线上. 11．已知某球体的体积与其表面积的数值相等，则此球体的半径为 12．函数 f(x) lg(1 x2),g(x)  2| x|,h(x) tg2x中， 是偶函数. 第2页 | 共10页x2 y2 13．以双曲线  1右顶点为顶点，左焦点为焦点的抛物线的方程是 16 9 14．将长度为1的铁丝分成两段，分别围成一个正方形和一个圆形，要使正方形与圆的面积 之和最小，正方形的周长应为 三、解答题：本大题共6小题，共84分.解答应写出文字说明，证明过程或演算步骤. 15．（本小题满分13分） 已知函数 f(x) cos4 x2sinxcosxsin4 x. （Ⅰ）求 f(x)的最小正周期； （Ⅱ）求 f(x)的最大值、最小值. 16．（本小题满分13分）   已知数列 a 是等差数列，且a  2,a a a 12. n 1 1 2 3   （Ⅰ）求数列 a 的通项公式； n （Ⅱ）令b  a 3n(xR).求数列  b  前n项和的公式. n n n 17．（本小题满分15分） 如图，正三棱柱ABC—ABC 中，D是BC的中点，AB=a. 1 1 1 （Ⅰ）求证：直线AD⊥BC； 1 1 1 （Ⅱ）求点D到平面ACC 的距离； 1 （Ⅲ）判断AB与平面ADC的位置关系， 1 并证明你的结论. 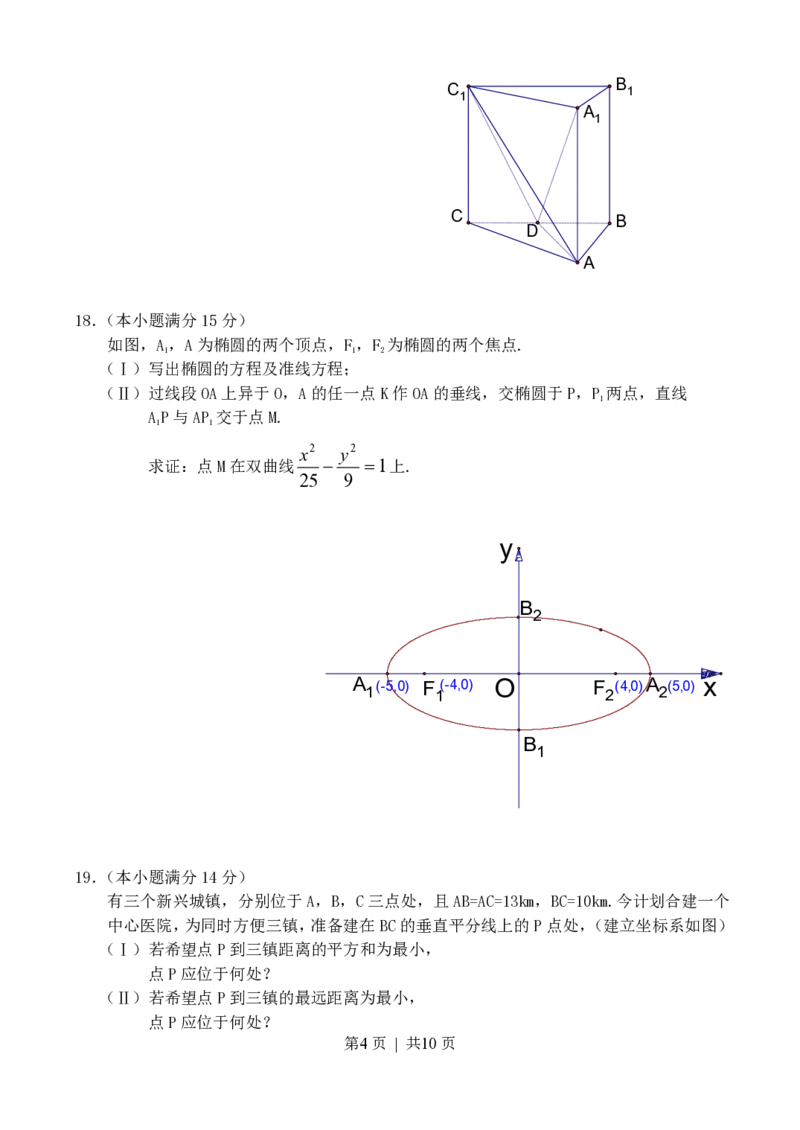第3页 | 共10页B C 1 1 A 1 C B D A 18．（本小题满分15分） 如图，A，A为椭圆的两个顶点，F，F 为椭圆的两个焦点. 1 1 2 （Ⅰ）写出椭圆的方程及准线方程； （Ⅱ）过线段OA上异于O，A的任一点K作OA的垂线，交椭圆于P，P 两点，直线 1 AP与AP 交于点M. 1 1 x2 y2 求证：点M在双曲线  1上. 25 9 y B 2 A 1 (-5,0) F 1 (-4,0) O F 2 (4,0)A 2 (5,0) x B 1 19．（本小题满分14分） 有三个新兴城镇，分别位于A，B，C三点处，且AB=AC=13km，BC=10km.今计划合建一个 中心医院，为同时方便三镇，准备建在BC的垂直平分线上的P点处，（建立坐标系如图） （Ⅰ）若希望点P到三镇距离的平方和为最小， 点P应位于何处？ （Ⅱ）若希望点P到三镇的最远距离为最小， 点P应位于何处？ 第4页 | 共10页y A P B(-b,0) O C(b,0) x 20．（本小题满分14分） 设y  f(x)是定义在区间[1,1]上的函数，且满足条件： （i） f(1)  f(1) 0; （ii）对任意的u,v[1,1],都有| f(u) f(v)||uv|. （Ⅰ）证明：对任意的x[1,1],都有x1 f(x)1x; 1 x,x[1,0) （Ⅱ）判断函数g(x)   是否满足题设条件； 1x,x[0,1] （Ⅲ）在区间[－1，1]上是否存在满足题设条件的函数y  f(x)，且使得对任意的 u,v[1,1],都有| f(u) f(v)|uv. 若存在，请举一例：若不存在，请说明理由. 一、选择题：本题考查基本知识和基本运算. 每小题5分，满分50分. 1．A 2．D 3．A 4．A 5．D 6．B 7．C 8．B 9．B 10．C 二、填空题：本题考查基本知识和基本运算.每小题4分,满分16分. 4 11．3 12． f(x);g(x) 13．y2  36(x4) 14． 4 三、解答题：本大题共6小题，共84分.解答应写出文字说明，证明过程或演算步骤. 15．本小题主要考查三角函数的倍角、和角公式，以及三角函数的性质等基本知识，考查运 第5页 | 共10页算能力，满分13分. （Ⅰ）解：因为 f(x) cos4 x2sinxcosxsin4 x (cos2 xsin2 x)(cos2 xsin2 x)sin2x  cos2xsin2x  2cos(2x ) 4 2 所以 f(x)的最小正周期T  . 2  （Ⅱ）解：因为 f(x)  2cos(2x ),所以 f(x)的最大值为 2 ,最小值为－ 2 4 16．本小题主要考查等差、等比数列等基本知识，考查综合运用数学知识和方法解决问题的 能力.满分13分. （Ⅰ）解：设数列{a }公差为d ，则 a a a 3a 3d 12,又a  2,d  2. n 1 2 3 1 1 所以a  2n. n （Ⅱ）解：由b  a 3n  2n3n,得 n n S 23432  (2n2)3n12n3n,① n  3S 232 433  (2n2)3n 2n3n1.② n  将①式减去②式，得 2S 2(332  3n)2n3n1 3(3n 1)2n3n1. n  所以 3(13n) S  n3n1. n 2 17．本小题主要考查直线与平面的位置关系，正棱柱的性质，棱锥的体积等基本知识，考查 空间想象能力和逻辑推理能力. 满分15分. （Ⅰ）证法一：∵点D是正△ABC中BC边的中点，∴AD⊥BC， 又AA⊥底面ABC，∴AD⊥BC ，∵BC∥BC，∴AD⊥BC. 1 1 1 1 1 1 1 证法二：连结AC，则AC=AB. ∵点D是正△ACB的底边中BC的中点， 1 1 1 1 1 ∴AD⊥BC ，∵BC∥BC，∴AD⊥BC. 1 1 1 1 1 1 （Ⅱ）解法一：作DE⊥AC于E， ∵平面ACC⊥平面ABC， 1 ∴DE⊥平面ACC 于E，即DE的长为点D到平面ACC 的 1 1 3 距离. 在Rt△ADC中，AC=2CD=a,AD a. 2 ∴所求的距离 CDAD 3 DE  a. AC 4 第6页 | 共10页C 1 B 1 A 1 C B D E A 解法二：设点D到平面ACC 的距离为x， 1 1 3 1 1 ∵体积V V   a2CC   aCC x. C 1 ACD 1 DACC 1 3 8 1 3 2 1 3 x a,即点D到平面ACC 1 的距离为 3 a . 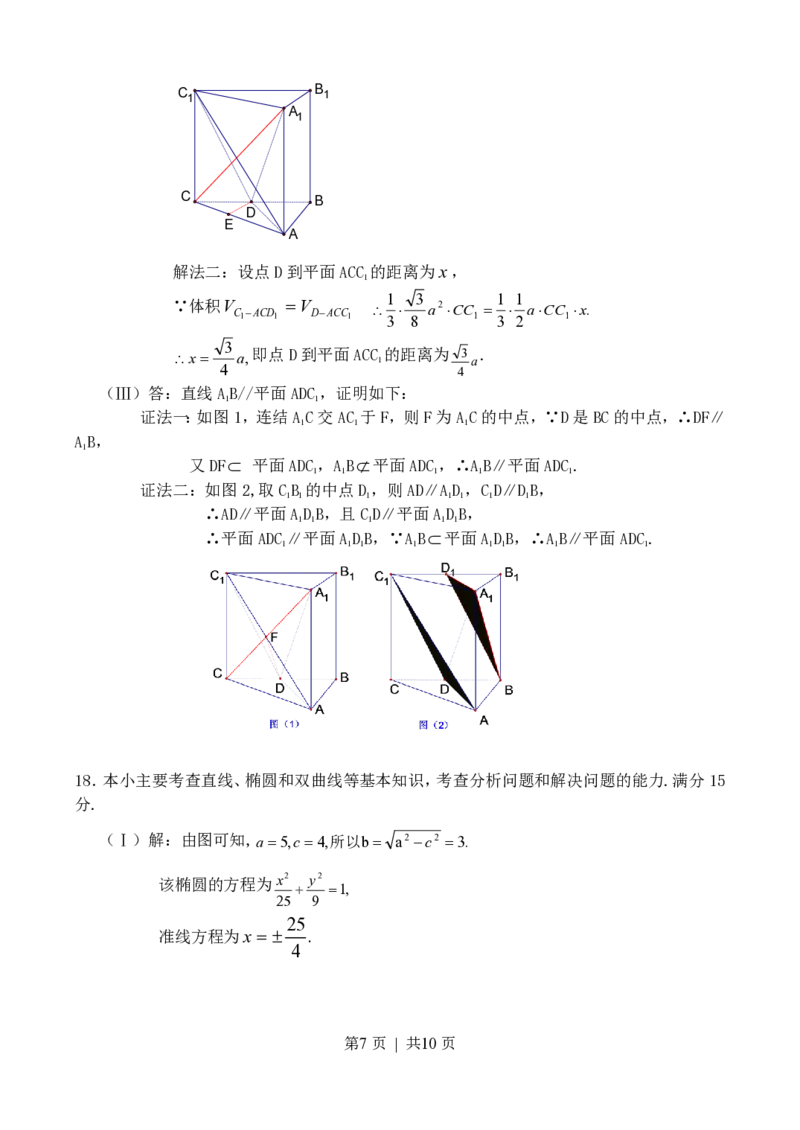4 4 （Ⅲ）答：直线AB//平面ADC，证明如下： 1 1 证法一：如图1，连结AC交AC 于F，则F为AC的中点，∵D是BC的中点，∴DF∥ 1 1 1 AB， 1 又DF 平面ADC，AB平面ADC，∴AB∥平面ADC. 1 1 1 1 1 证法二：如图2,取CB 的中点D，则AD∥AD，CD∥DB， 1 1 1 1 1 1 1 ∴AD∥平面ADB，且CD∥平面ADB， 1 1 1 1 1 ∴平面ADC∥平面ADB，∵AB平面ADB，∴AB∥平面ADC. 1 1 1 1 1 1 1 1 18．本小主要考查直线、椭圆和双曲线等基本知识，考查分析问题和解决问题的能力.满分15 分. （Ⅰ）解：由图可知,a5,c4,所以b a2 c2 3. 该椭圆的方程为x2 y2  1, 25 9 25 准线方程为x   . 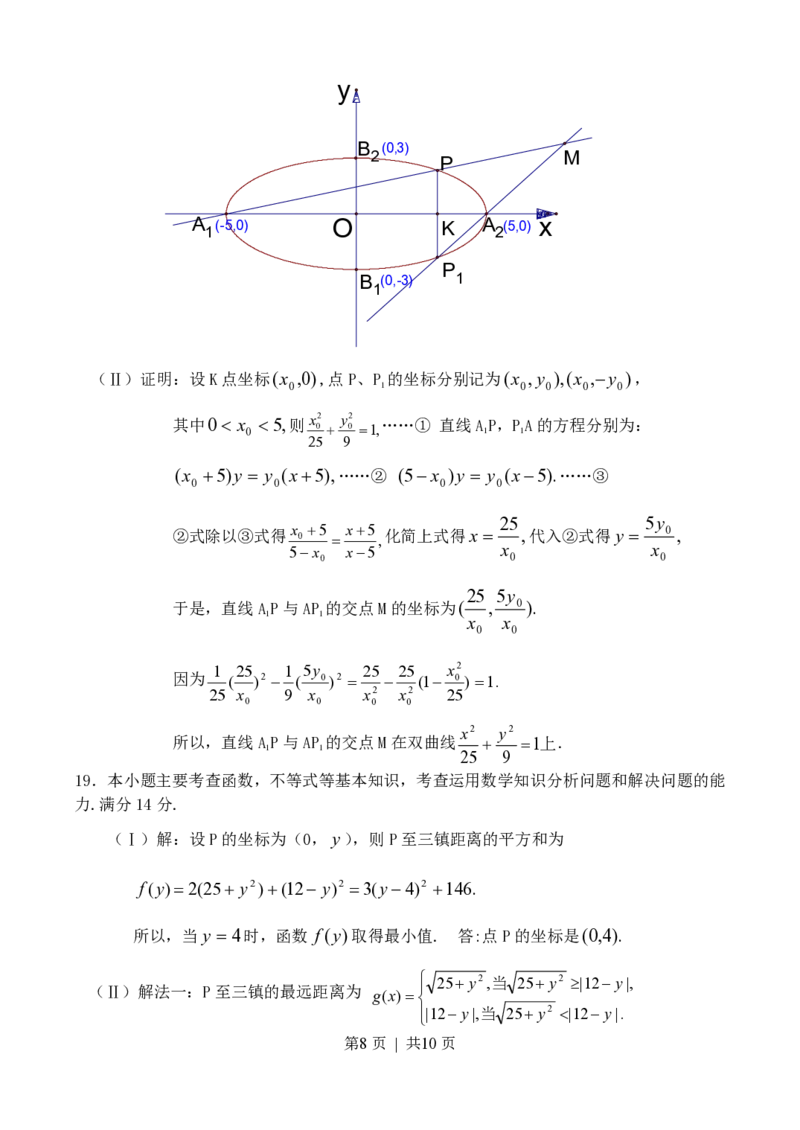4 第7页 | 共10页y B (0,3) 2 M P A (-5,0) O K A (5,0) x 1 2 P B (0,-3) 1 1 （Ⅱ）证明：设K点坐标(x ,0),点P、P 的坐标分别记为(x ,y ),(x ,y )， 0 1 0 0 0 0 其中0 x 5,则x2 y2 ……① 直线AP，PA的方程分别为： 0 0  0 1, 1 1 25 9 (x 5)y  y (x5),……② (5x )y  y (x5).……③ 0 0 0 0 25 5y ②式除以③式得 x 0 5  x5 , 化简上式得x  ,代入②式得y  0 , 5x x5 x x 0 0 0 25 5y 于是，直线AP与AP 的交点M的坐标为( , 0). 1 1 x x 0 0 1 25 1 5y 25 25 x2 因为 ( )2  ( 0)2   (1 0 )1. 25 x 9 x x2 x2 25 0 0 0 0 x2 y2 所以，直线AP与AP 的交点M在双曲线  1上. 1 1 25 9 19．本小题主要考查函数，不等式等基本知识，考查运用数学知识分析问题和解决问题的能 力.满分14分. （Ⅰ）解：设P的坐标为（0，y），则P至三镇距离的平方和为 f(y)2(25 y2)(12 y)2 3(y4)2 146. 所以，当y  4时，函数 f(y)取得最小值. 答:点P的坐标是(0,4). 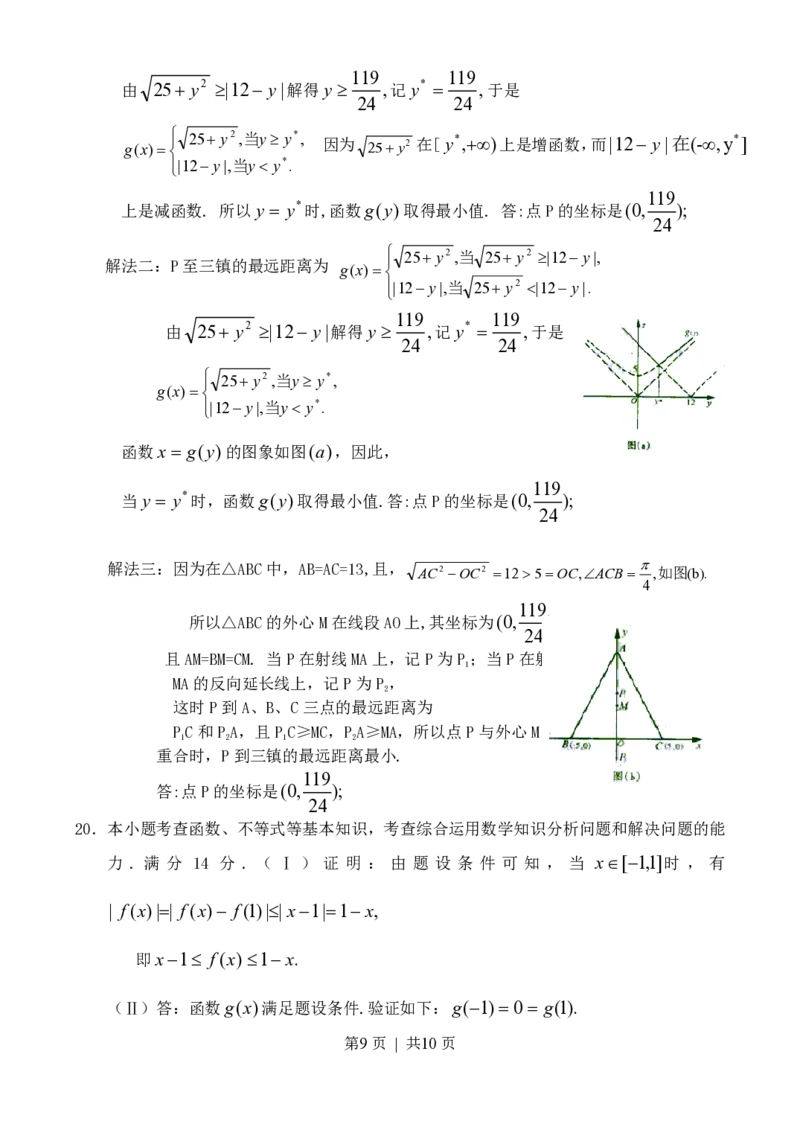（Ⅱ）解法一：P至三镇的最远距离为   25y2,当 25y2 |12y|, g(x) |12y|,当 25y2 |12y|.  第8页 | 共10页119 119 由 25 y2 |12 y|解得y  ,记y*  ,于是 24 24 g(x)    25y2,当y y*, 因为 25y2 在[y*,)上是增函数，而|12 y|在(-,y*]  |12y|,当y y*. 119 上是减函数. 所以y  y*时,函数g(y)取得最小值. 答:点P的坐标是(0, ); 24 解法二：P至三镇的最远距离为   25y2,当 25y2 |12y|, g(x) |12y|,当 25y2 |12y|.  119 119 由 25 y2 |12 y|解得y  ,记y*  ,于是 24 24   25y2,当y y*, g(x)  |12y|,当y y*. 函数x  g(y)的图象如图(a)，因此， 119 当y  y*时，函数g(y)取得最小值.答:点P的坐标是(0, ); 24 解法三：因为在△ABC中，AB=AC=13,且， AC2 OC2 125OC,ACB  ,如图(b). 4 119 所以△ABC的外心M在线段AO上,其坐标为(0, ), 24 且AM=BM=CM. 当P在射线MA上，记P为P；当P在射线 1 MA的反向延长线上，记P为P， 2 这时P到A、B、C三点的最远距离为 PC和PA，且PC≥MC，PA≥MA，所以点P与外心M 1 2 1 2 重合时，P到三镇的最远距离最小. 119 答:点P的坐标是(0, ); 24 20．本小题考查函数、不等式等基本知识，考查综合运用数学知识分析问题和解决问题的能 力 . 满 分 14 分 . （ Ⅰ ） 证 明 ： 由 题 设 条 件 可 知 ， 当 x[1,1]时 ， 有 | f(x)|| f(x) f(1)|| x1|1x, 即x1 f(x)1x. （Ⅱ）答：函数g(x)满足题设条件.验证如下：g(1) 0  g(1). 第9页 | 共10页对任意的u,v[1,1]， 当u,v[0,1]时,有| g(u)g(v)||(1u)(1v)||uv|; 当u,v[-1,0]时,同理有| g(u)g(v)||uv|; 当uv 0,不妨设u[1,0),v(0,1], 有| g(u)g(v)||(1u)(1v)||uv||vu|. 所以，函数g(x)满足题设条件. （Ⅲ）答：这样满足的函数不存在.理由如下： 假设存在函数 f(x)满足条件，则由 f(1)  f(1) 0,得| f(1) f(1)|0,① 由于对任意的u,v[1,1]，都有| f(u) f(v)||uv|. 所以，| f(1) f(1)||1(1)| 2.② ①与②矛盾，因此假设不成立，即这样的函 数不存在. 第10页 | 共10页