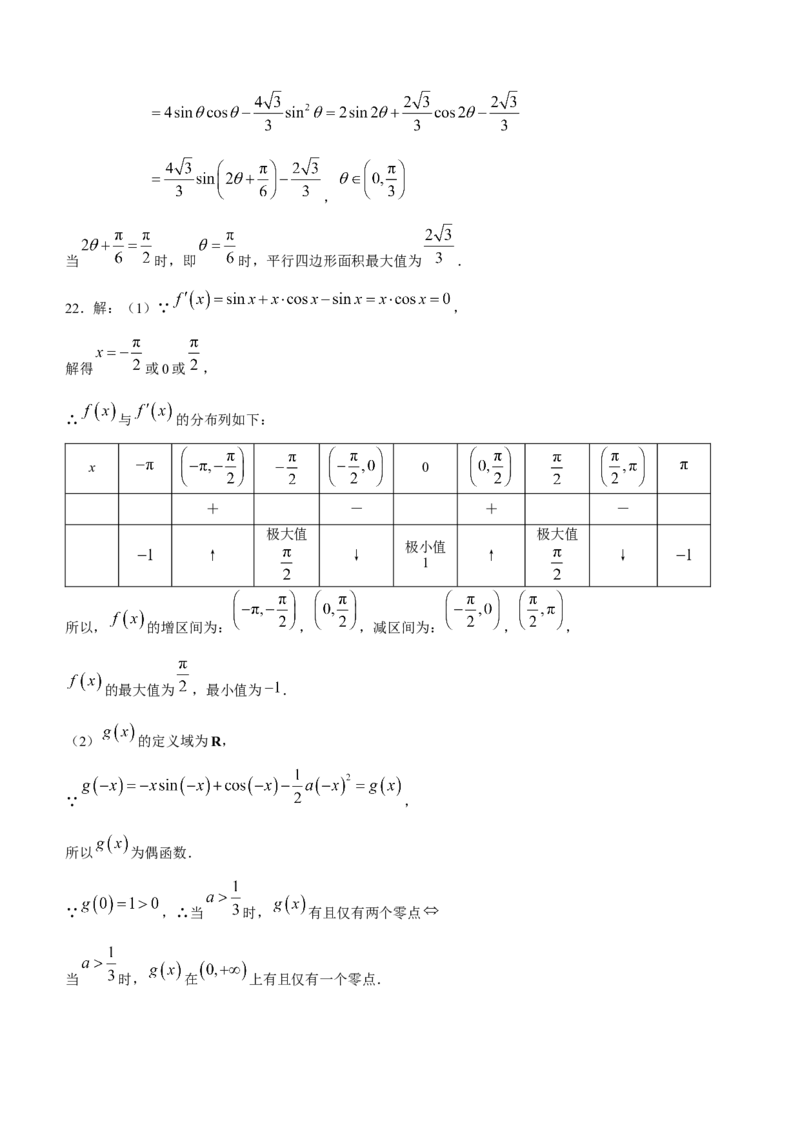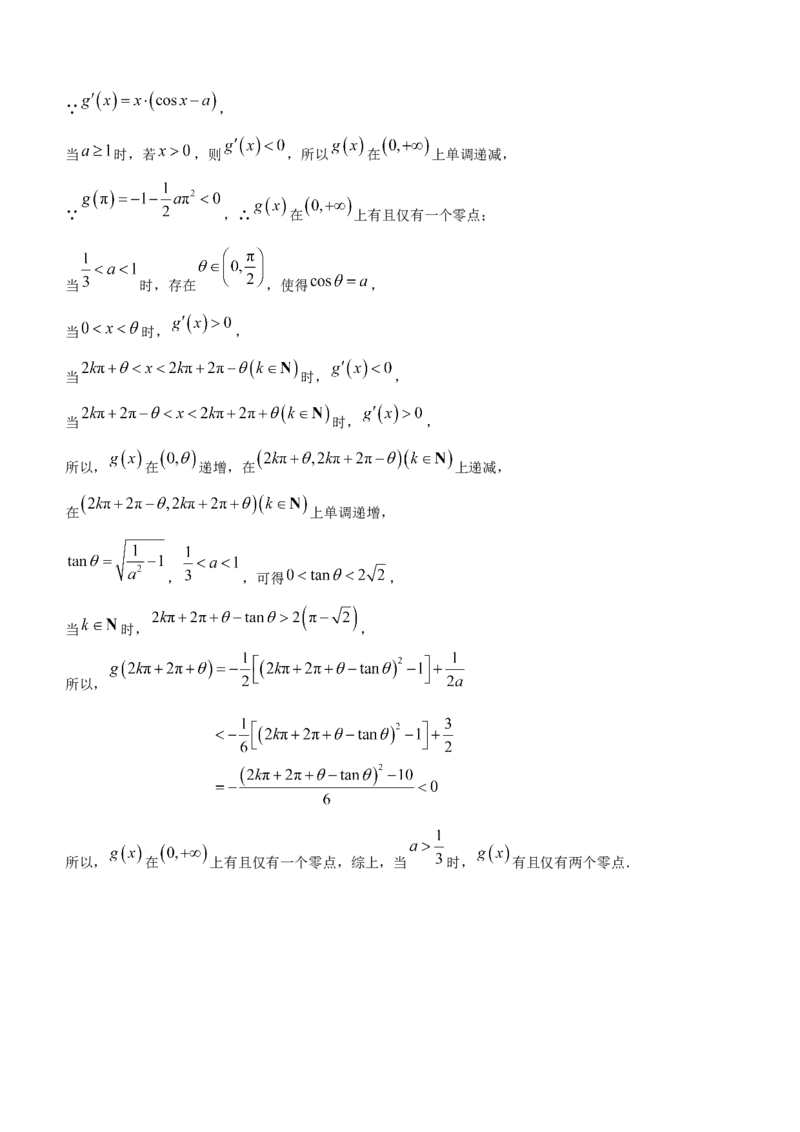文档内容
保密★启用前
准考证号__________ 姓名__________
(在此卷上答题无效)
2023~2024 学年高中毕业班第一学期期中考试
数学试题
2023.11
一、单选题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
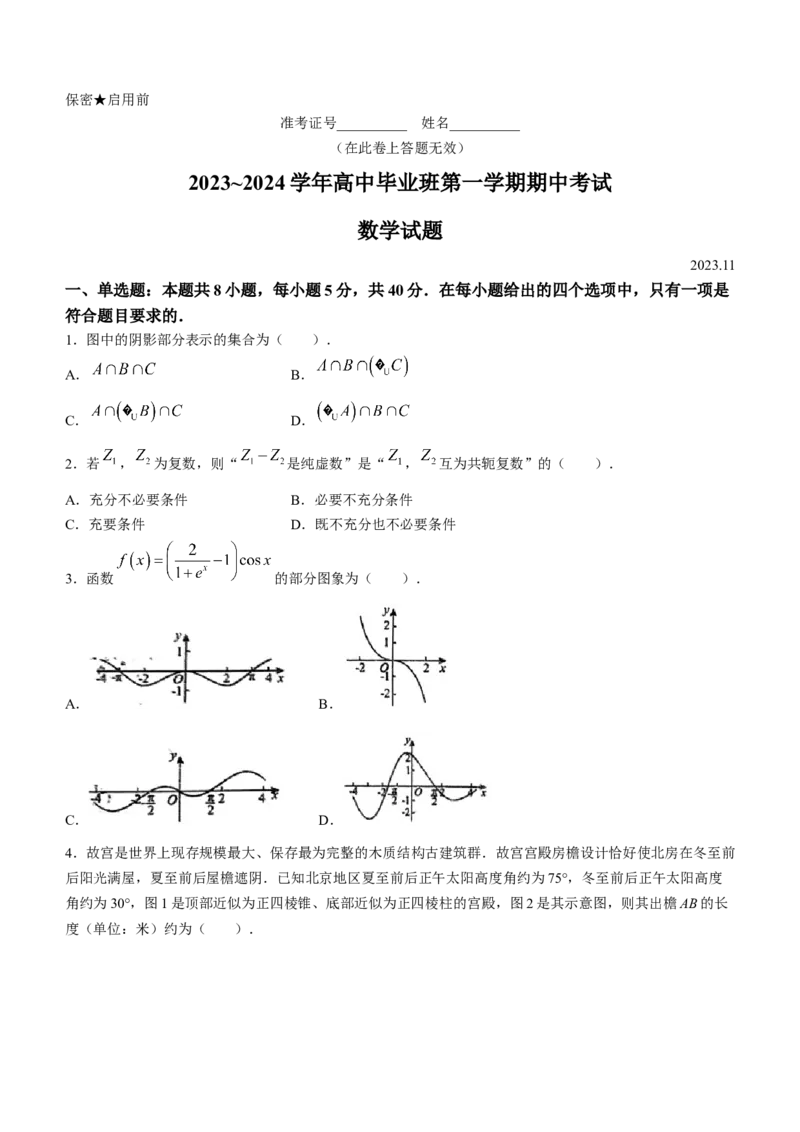
1.图中的阴影部分表示的集合为( ).
A. B.
C. D.
2.若 , 为复数,则“ 是纯虚数”是“ , 互为共轭复数”的( ).
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
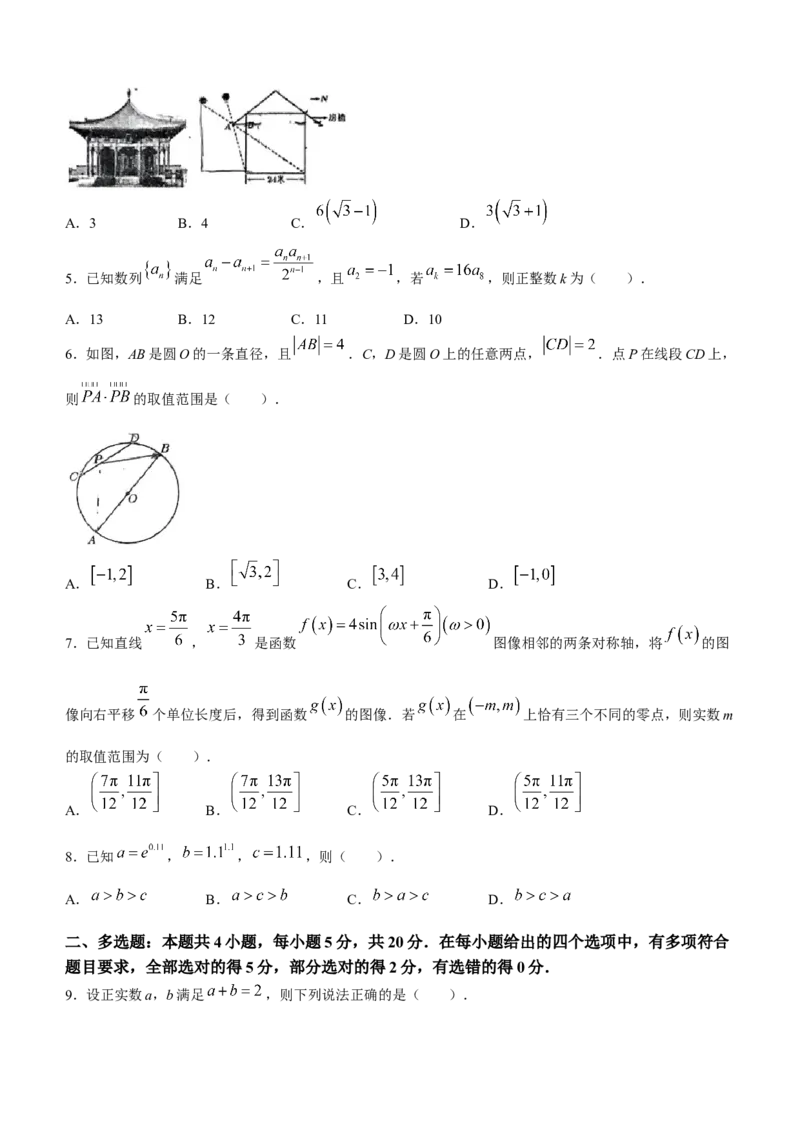
3.函数 的部分图象为( ).
A. B.
C. D.
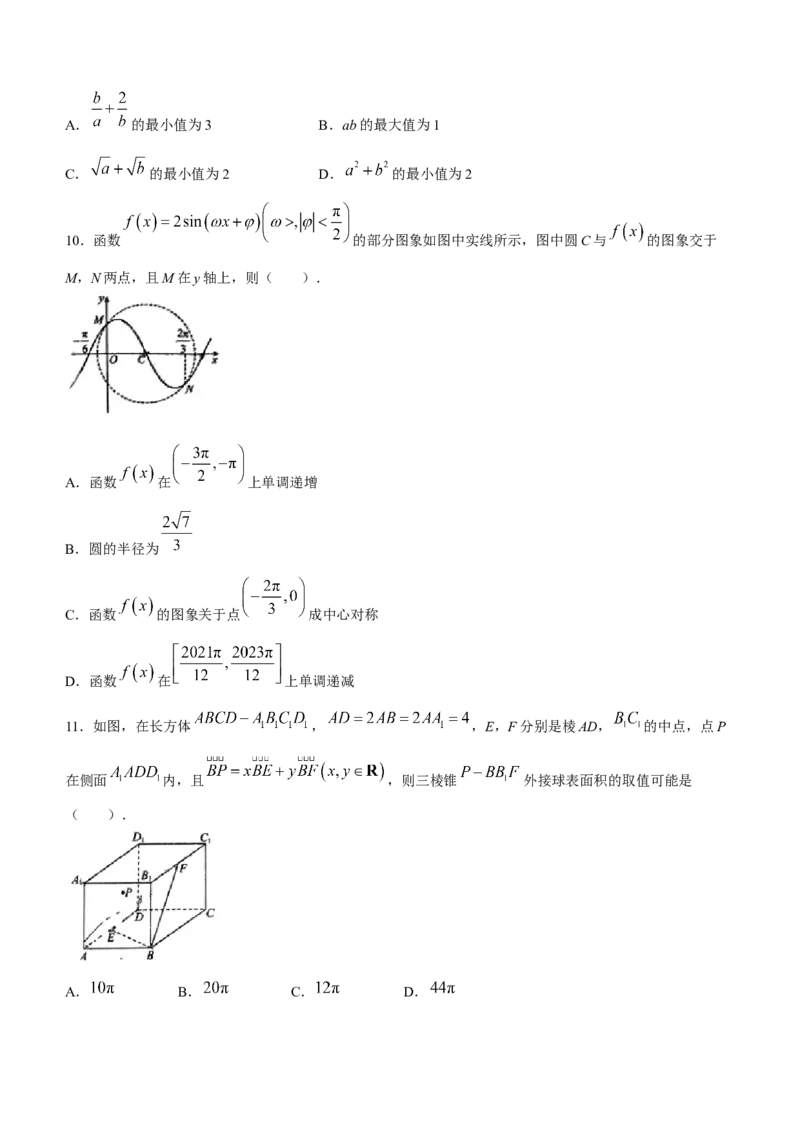
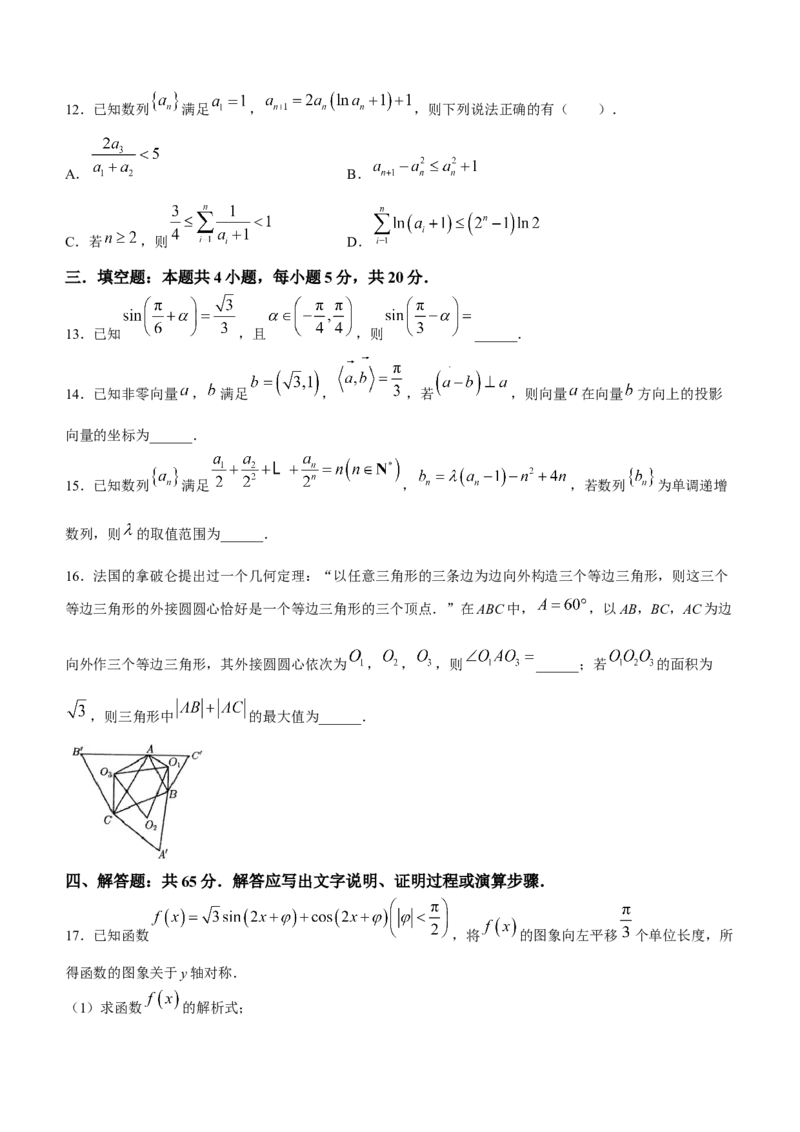
4.故宫是世界上现存规模最大、保存最为完整的木质结构古建筑群.故宫宫殿房檐设计恰好使北房在冬至前
后阳光满屋,夏至前后屋檐遮阴.已知北京地区夏至前后正午太阳高度角约为75°,冬至前后正午太阳高度
角约为30°,图1是顶部近似为正四棱锥、底部近似为正四棱柱的宫殿,图2是其示意图,则其出檐AB的长
度(单位:米)约为( ).
学科网(北京)股份有限公司A.3 B.4 C. D.
5.已知数列 满足 ,且 ,若 ,则正整数k为( ).
A.13 B.12 C.11 D.10
6.如图,AB是圆O的一条直径,且 .C,D是圆O上的任意两点, .点P在线段CD上,
则 的取值范围是( ).
A. B. C. D.
7.已知直线 , 是函数 图像相邻的两条对称轴,将 的图
像向右平移 个单位长度后,得到函数 的图像.若 在 上恰有三个不同的零点,则实数m
的取值范围为( ).
A. B. C. D.
8.已知 , , ,则( ).
A. B. C. D.
二、多选题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合
题目要求,全部选对的得5分,部分选对的得2分,有选错的得0分.
9.设正实数a,b满足 ,则下列说法正确的是( ).
学科网(北京)股份有限公司A. 的最小值为3 B.ab的最大值为1
C. 的最小值为2 D. 的最小值为2
10.函数 的部分图象如图中实线所示,图中圆C与 的图象交于
M,N两点,且M在y轴上,则( ).
A.函数 在 上单调递增
B.圆的半径为
C.函数 的图象关于点 成中心对称
D.函数 在 上单调递减
11.如图,在长方体 , ,E,F分别是棱AD, 的中点,点P
在侧面 内,且 ,则三棱锥 外接球表面积的取值可能是
( ).
A. B. C. D.
学科网(北京)股份有限公司12.已知数列 满足 , ,则下列说法正确的有( ).
A. B.
C.若 ,则 D.
三.填空题:本题共4小题,每小题5分,共20分.
13.已知 ,且 ,则 ______.
14.已知非零向量 , 满足 , ,若 ,则向量 在向量 方向上的投影
向量的坐标为______.
15.已知数列 满足 , ,若数列 为单调递增
数列,则 的取值范围为______.
16.法国的拿破仑提出过一个几何定理:“以任意三角形的三条边为边向外构造三个等边三角形,则这三个
等边三角形的外接圆圆心恰好是一个等边三角形的三个顶点.”在ABC中, ,以AB,BC,AC为边
向外作三个等边三角形,其外接圆圆心依次为 , , ,则 ______;若 的面积为
,则三角形中 的最大值为______.
四、解答题:共65分.解答应写出文字说明、证明过程或演算步骤.
17.已知函数 ,将 的图象向左平移 个单位长度,所
得函数的图象关于y轴对称.
(1)求函数 的解析式;
学科网(北京)股份有限公司(2)若关于x的方程 在 上恰有两个实数根,求实数a的取值范围.
18.已知函数 .
(1)讨论函数 的单调性;
(2)若 ,是否存在整数 ,都有 恒成立,若存在求出实数m的最小值,
若不存在说明理由.
19.设数列 前n项和 满足 , .
(1)证明:数列 为等比数列;
(2)记 ,求数列 的前n项和 .
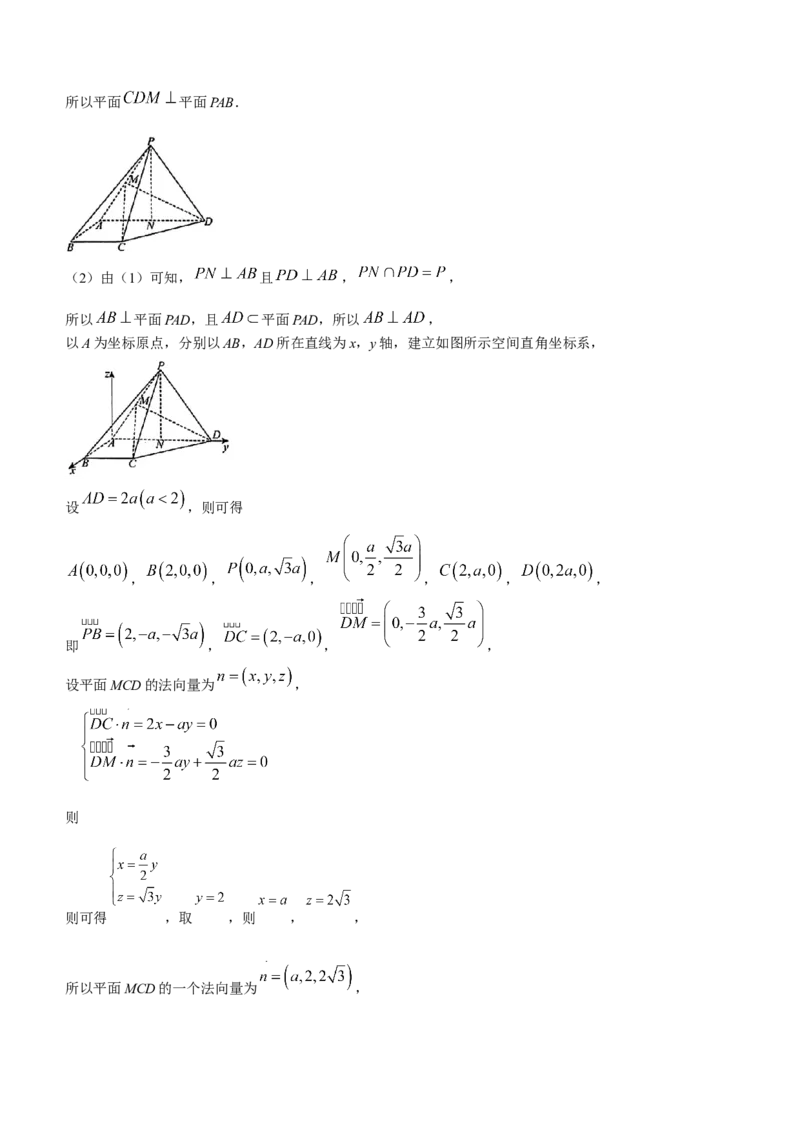
20.如图,在四棱锥 中,PAD为等边三角形,M为PA的中点, ,平面 平面
ABCD.
(1)证明:平面 平面PAB;
(2)若 , , ,直线PB与平面MCD所成角的正弦值为 ,求三棱锥
的体积.
21.如图,在海岸线EF一侧有一休闲游乐场,游乐场的前一部分边界为曲线段FGBC,该曲线段是函数
, 的图像,图像的最高点为 .边界的中间
部分为长1千米的直线段CD,且 ,游乐场的后一部分边界是以O为圆心的一段圆弧DE.
学科网(北京)股份有限公司(1)求曲线段FGBC的函数表达式;
(2)曲线段FGBC上的入口G距海岸线EF最近距离为1千米,现准备从入口G修一条笔直的景观路到O,
求景观路GO长;
(3)如图,在扇形ODE区域内建一个平行四边形休闲区OMPQ,平行四边形的一边在海岸线EF上,一边
在半径OD上,另外一个顶点P在圆弧DE上,且 ,求平行四边形休闲区OMPQ面积的最大值及
此时 的值.
22.已知函数 .
(1)求 在 的单调区间与最值;
(2)当 时,若 ,证明: 有且仅有两个零点.
2023 年~2024 学年高中毕业班第一学期期中考试
数学评分参考标准
一、单选题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
1 2 3 4 5 6 7 8
B D C C B D A A
二、多选题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合
题目要求,全部选对的得5分,部分选对的得2分,有选错的得0分.
9 10 11 12
ABD CD BCD BCD
三、填空题:本题共4小题,每小题5分,共20分.
13. 14. 15. 16. ,4
四、解答题:共65分.解答应写出文字说明、证明过程或演算步骤.
学科网(北京)股份有限公司17.解:(1) ,
将函数 的图象向左平移 个单位长度后,
所得函数为 ,
∴ , ,∴ , .
又 ,∴ ,∴ .
(2)∵ ,∴ ,
当 ,即 时, 单调递增;
当 ,即 时, 单调递减.
且 , , .
∵方程 在 上恰有两个实数根,
∴ ,∴实数a的取值范围为 .
18.解:(1)∵ , ,
当 , ,∴ 在 单调递增,
当 时, ,
令 ,得 , 得 ,
学科网(北京)股份有限公司∴ 在 单调递增,在 单调递减.
综上, 时, 在 单调递增;
当 时, 在 单调递增,在 单调递减.
(2)∵ ,∴ ,
∴ ,∴ ,
令 ,∴ ,
令 , ,∴ 在 单调递减.
∵
∵ ,
∴ ,使得 ,即 , ,
当 , , , 单调递增,
当 , , , 单调递减,
∴ ,
∵ , ,∴ ,∴m的最小值为3.
19.(1)证明:∵ ,且 ,
学科网(北京)股份有限公司∴ ,
∴ ,∴ ,
令 ,可得 ,∴ ,
所以数列 是首项为 ,公比为 的等比数列.
(2)由(1)可得 ,
∴ ,∴ ,
∴ ,
∴ .
20.【解析】(1)取AD中点为N,连接PN,
因为PAD为等边三角形,所以 ,
且平面 平面ABCD,平面 平面 , 面PAD,
所以 平面ABCD,
又 平面ABCD,所以 ,
又因为 , ,PN, 平面PAD,
所以 平面PAD,
又因为 平面PAD,所以 ,
因为M为AP中点,所以 ,且 ,PA, 平面PAD,
所以 平面PAB,且 平面CDM,
学科网(北京)股份有限公司所以平面 平面PAB.
(2)由(1)可知, 且 , ,
所以 平面PAD,且 平面PAD,所以 ,
以A为坐标原点,分别以AB,AD所在直线为x,y轴,建立如图所示空间直角坐标系,
设 ,则可得
, , , , , ,
即 , , ,
设平面MCD的法向量为 ,
则
则可得 ,取 ,则 , ,
所以平面MCD的一个法向量为 ,
学科网(北京)股份有限公司设直线PB与平面MCD所成角为 ,
所以 ,
解得 ,或 ,即 (舍去)或1,
所以 , .
21.解:(1)由已知条件,得 ,
又∵ , ,∴ .
又∵当 时,有 ,∴ ,
∴曲线段FBC的解析式为 , .
(2)由 得 ,
又 ,∴ , ,∴ , ,
∴景观路GO长为 千米.
(3)如图, , ,∴ , ,
作 轴于 点,在 中, ,
在 中, ,
∴ ,
学科网(北京)股份有限公司,
当 时,即 时,平行四边形面积最大值为 .
22.解:(1)∵ ,
解得 或0或 ,
∴ 与 的分布列如下:
x 0
+ - + -
极大值 极大值
极小值
↑ ↓ ↑ ↓
1
所以, 的增区间为: , ,减区间为: , ,
的最大值为 ,最小值为 .
(2) 的定义域为R,
∵ ,
所以 为偶函数.
∵ ,∴当 时, 有且仅有两个零点
当 时, 在 上有且仅有一个零点.
学科网(北京)股份有限公司∵ ,
当 时,若 ,则 ,所以 在 上单调递减,
∵ ,∴ 在 上有且仅有一个零点;
当 时,存在 ,使得 ,
当 时, ,
当 时, ,
当 时, ,
所以, 在 递增,在 上递减,
在 上单调递增,
, ,可得 ,
当 时, ,
所以,
所以, 在 上有且仅有一个零点,综上,当 时, 有且仅有两个零点.
学科网(北京)股份有限公司