福建省莆田锦江中学2023-2024学年高三上学期期中考试数学(1)_2023年11月_01每日更新_23号_2024届福建省莆田锦江中学高三上学期期中考试

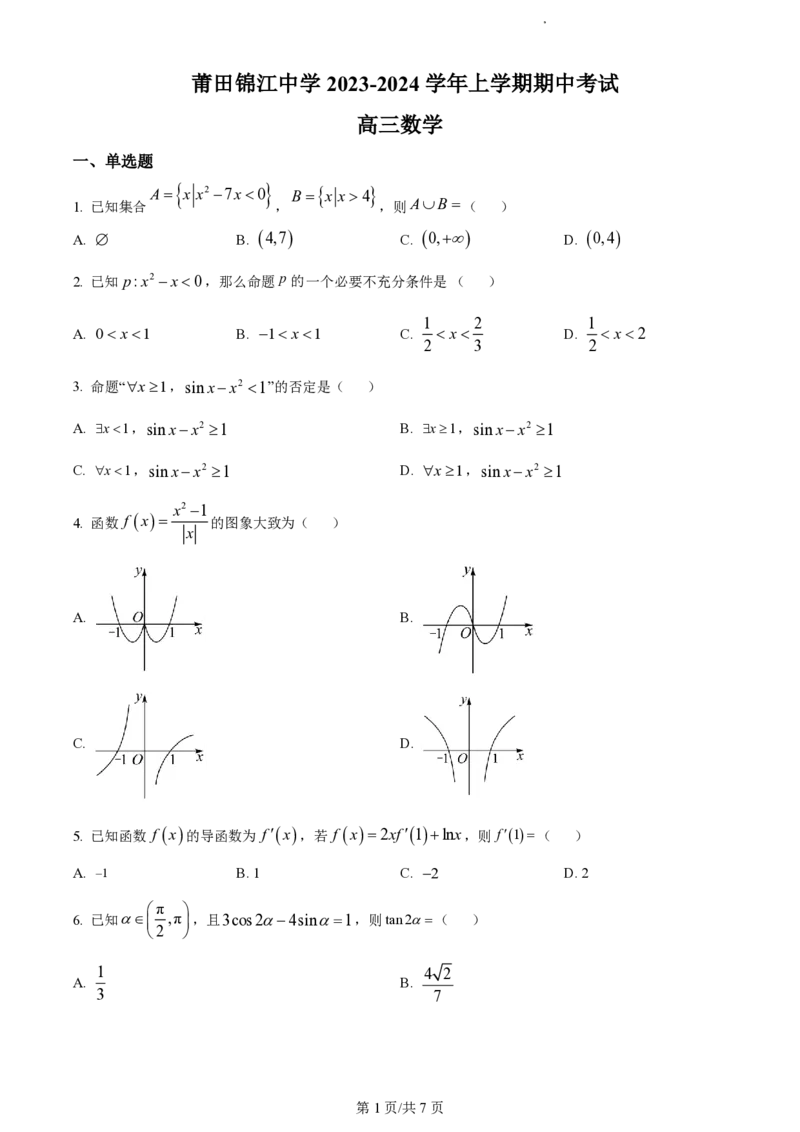
莆田锦江中学 2023-2024 学年上学期期中考试 高三数学 一、单选题   A x x2 7x0 B  x x4  1. 已知集合 ， ，则AB（ ） A.  B. 4,7 C. 0, D. 0,4 2. 已知 p:x2 x0，那么命题 p 的一个必要不充分条件是 （ ） 1 2 1 A. 0 x1 B. 1 x1 C.  x D.  x2 2 3 2 3. 命题“x1，sinxx2 1”的否定是（ ） A. x1，sinxx2 1 B. x1，sinxx2 1 C. x1，sinxx2 1 D. x1，sinxx2 1 x2 1 4. 函数 f x 的图象大致为（ ） x A. B. C. D. 5. 已知函数 f x 的导函数为 f x ，若 f x2xf1lnx，则 f1（ ） A. 1 B. 1 C. 2 D. 2 π  6. 已知  ,π ，且3cos24sin1，则tan2（ ） 2  1 4 2 A. B. 3 7 第1页/共7页1 4 2 C.  D.  3 7 7. 第19届亚运会将于2023年9月23日至10月8日在杭州举行，甲､乙等4名杭州亚运会志愿者到游泳､ 射击､体操三个场地进行志愿服务，每名志愿者只去一个场地，每个场地至少一名志愿者，若甲不去游泳 场地，则不同的安排方法共有（ ） A. 12种 B. 18种 C. 24种 D. 36种 8. 数学来源于生活，约3000年以前，我国人民就创造出了属于自己的计数方法．十进制的算筹计数法就是 中国数学史上一个伟大的创造，算筹实际上是一根根同长短的小木棍．下图是利用算筹表示数1～9的一种 方法．例如：3可表示为“”，26可表示为“ ”，现有5根算筹，据此表示方法，若算筹不能剩余，则用 1～9这9个数字表示的所有两位数中，个位数与十位数之和为5的概率是（ ） 1 5 7 1 A. B. C. D. 3 12 2 12 二、多选题 1x 9. 关于函数 f xln ，下列选项中正确的有（ ） 1x A. f x 的定义域为 ,1U1, B. f x 为奇函数 C. f x 在定义域上是增函数 D. 函数 f x 与y ln1xln1x 是同一个函数 π 10. 已知函数 f x 的图象是由函数y 2sinxcosx的图象向右平移 个单位得到，则（ ） 6 A. f x 的最小正周期为π  π π B. f x 在区间   ,  上单调递增  6 3 π C. f x 的图象关于直线x 对称 3 π  D. 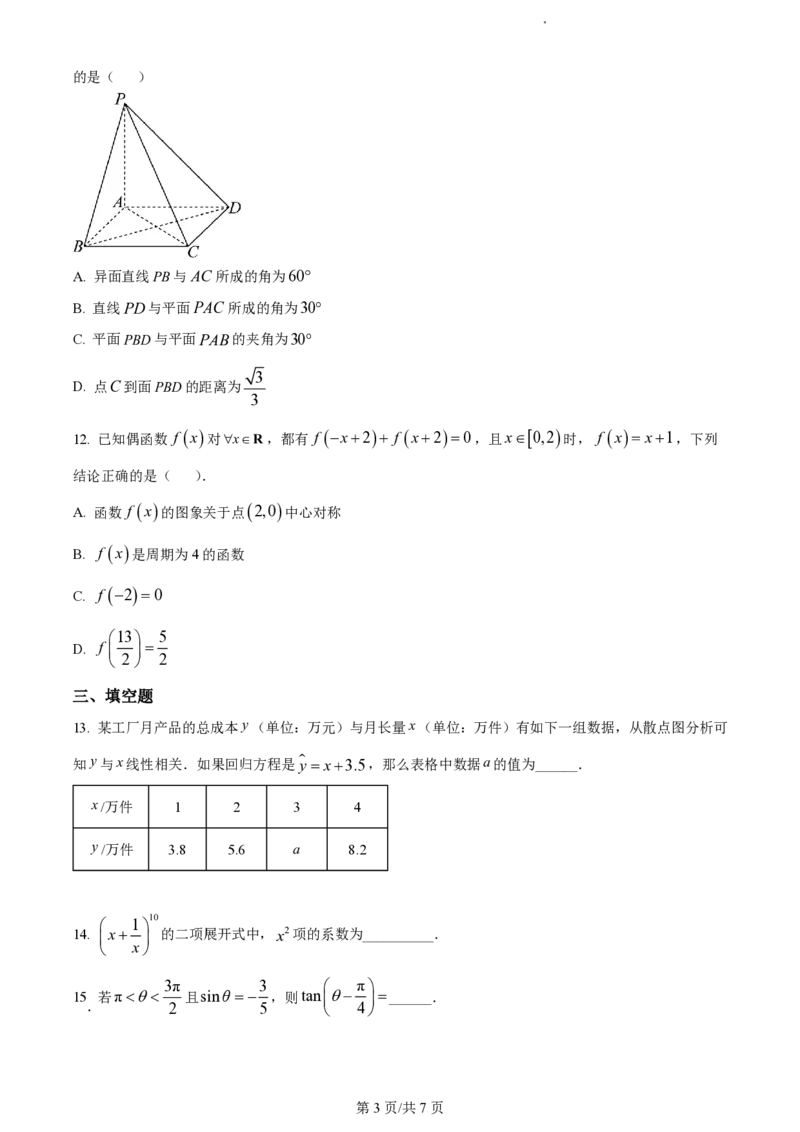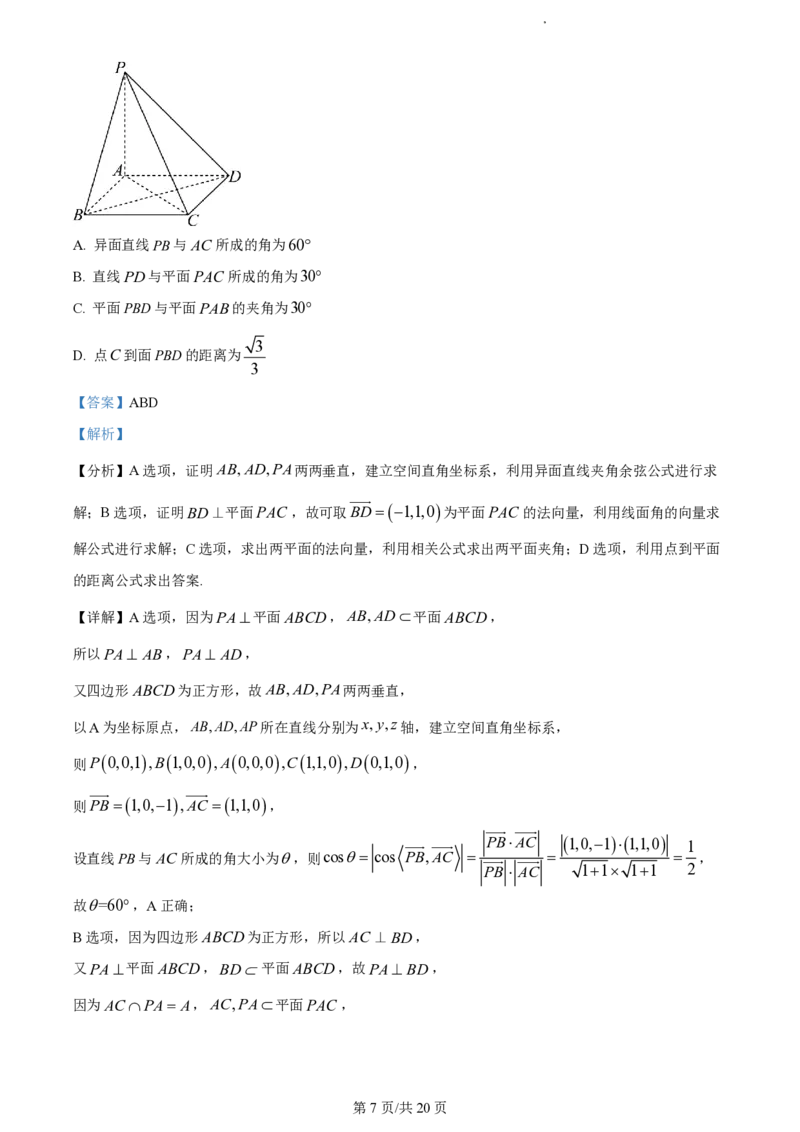f x 的图象关于点 ,0 对称 6  11. 如图，在底面为正方形的四棱锥PABCD中，PA平面ABCD，AP AB1，则下列说法正确 第2页/共7页的是（ ） A. 异面直线PB与AC所成的角为60 B. 直线PD与平面PAC 所成的角为30 C. 平面PBD与平面PAB的夹角为30 3 D. 点C到面PBD的距离为 3 12. 已知偶函数 f x 对xR，都有 f x2 f x20，且x0,2 时， f x x1，下列 结论正确的是（ ）． A. 函数 f x 的图象关于点 2,0 中心对称 B. f x 是周期为4的函数 C. f 20 13 5 D. f     2  2 三、填空题 13. 某工厂月产品的总成本y（单位：万元）与月长量x（单位：万件）有如下一组数据，从散点图分析可 知y与x线性相关．如果回归方程是y  x3.5，那么表格中数据a的值为______． x/万件 1 2 3 4 y/万件 3.8 5.6 a 8.2 10  1 14.  x  的二项展开式中，x2项的系数为__________．  x 3π 3  π 15 若π 且sinθ  ，则tan    ______． . 2 5  4 第3页/共7页16. 我们将服从二项分布的随机变量称为二项随机变量，服从正态分布的随机变量称为正态随机变量.概率 论中有一个重要的结论是棣莫弗—拉普拉斯极限定理，它表明，若随机变量Y ~ Bn,p ，当n充分大 时，二项随机变量Y 可以由正态随机变量X 来近似，且正态随机变量X 的期望和方差与二项随机变量Y 1 的期望和方差相同.棣莫弗在1733年证明了P 的特殊情形.1812年，拉普拉斯对一般的P进行了证明. 2 现抛掷一枚质地均匀的硬币100次，则利用正态分布近似估算硬币正面向上次数不超过60次的概率为 ______. （附：若X  N  ,2 ，则P X 0.683，P2 X 20.954， P3 X 30.997） 四、解答题  π  π 17. 已知函数 f xsin  2x  sin  2x   3cos2x.  3  3 （1）求函数 f(x)的最小正周期；  π （2）当x  0,  时，求函数 f(x)的单调递减区间和值域. 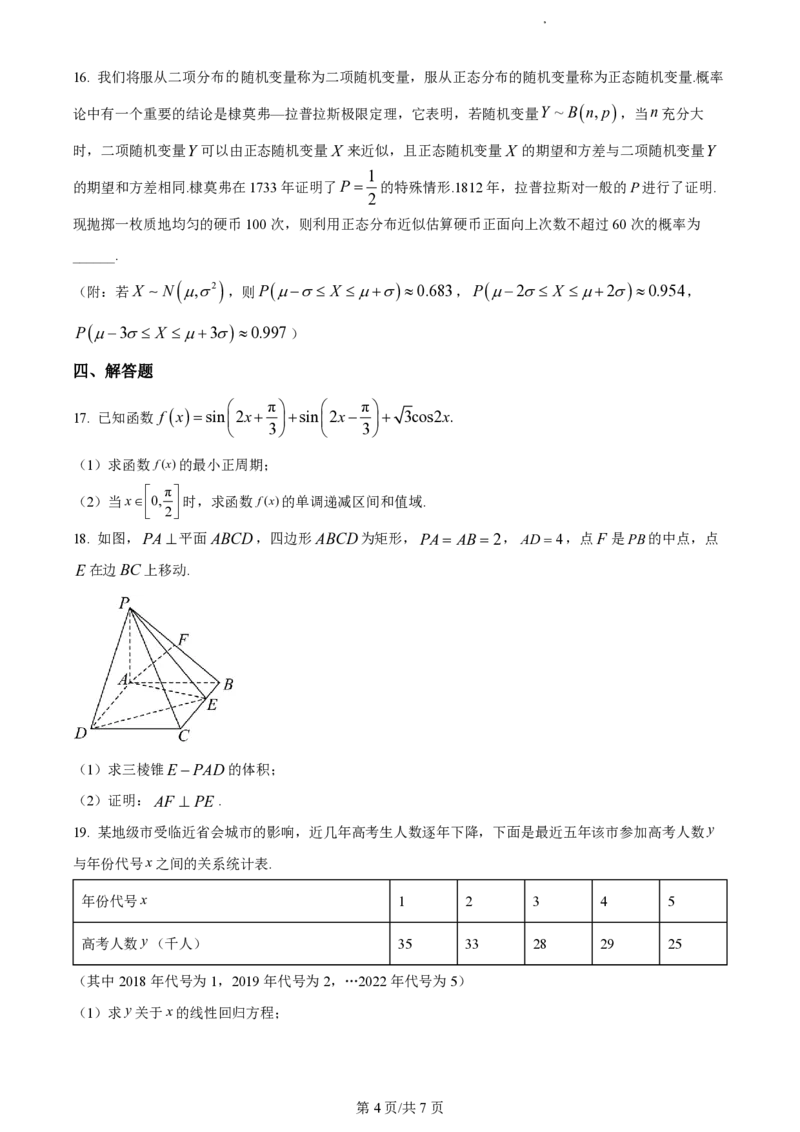 2 18. 如图，PA平面ABCD，四边形ABCD为矩形，PA AB2，AD4，点F 是PB的中点，点 E在边BC上移动. （1）求三棱锥EPAD的体积； （2）证明：AF  PE. 19. 某地级市受临近省会城市的影响，近几年高考生人数逐年下降，下面是最近五年该市参加高考人数y 与年份代号x之间的关系统计表. 年份代号x 1 2 3 4 5 高考人数y（千人） 35 33 28 29 25 （其中2018年代号为1，2019年代号为2，…2022年代号为5） （1）求y关于x的线性回归方程； 第4页/共7页（2）根据（1）的结果预测该市2023年参加高考的人数； （3）试分析该市参加高考人数逐年减少的原因. 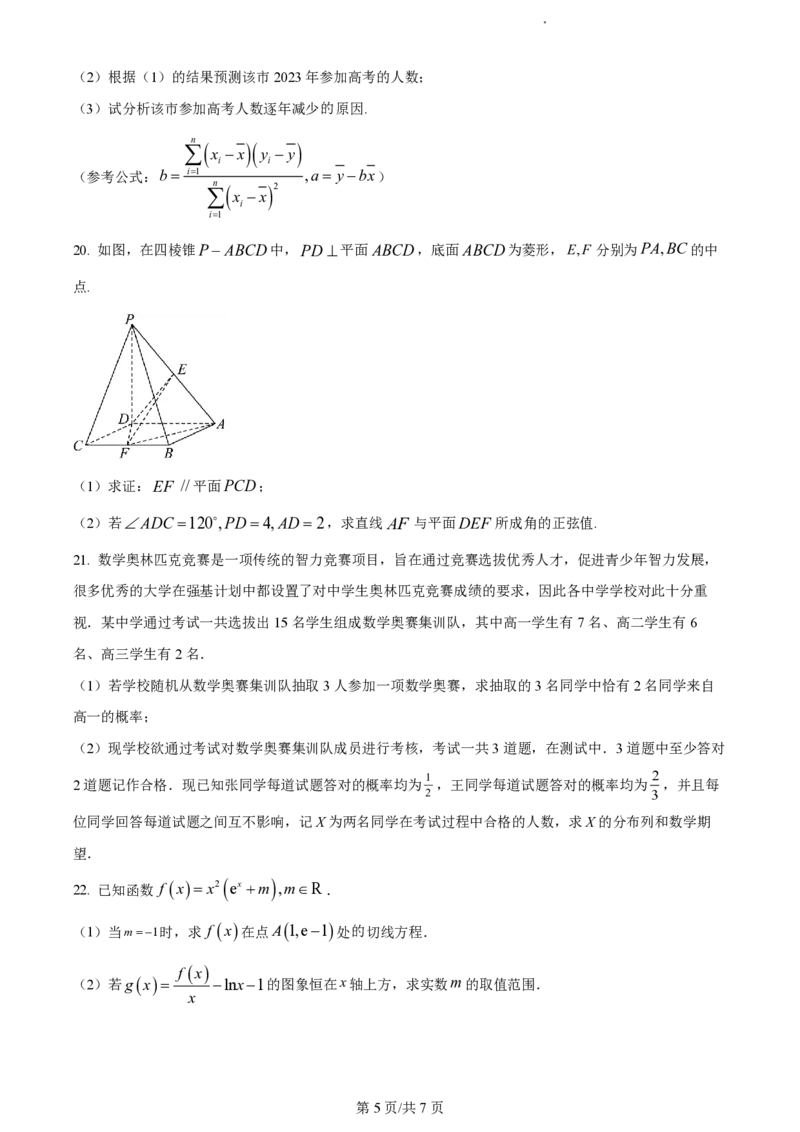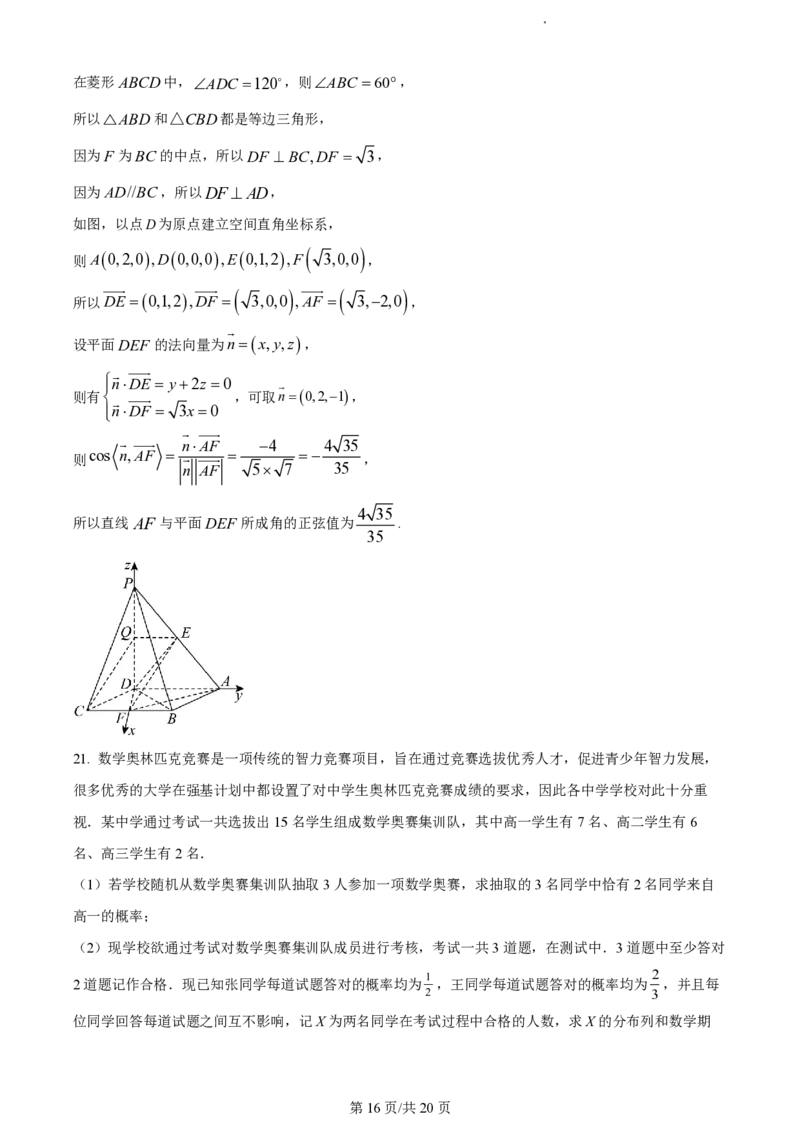n  x x  y  y  i i （参考公式：b i1 ,a ybx）  n  x x 2 i i1 20. 如图，在四棱锥PABCD中，PD 平面ABCD，底面ABCD为菱形，E,F 分别为PA,BC的中 点. （1）求证：EF //平面PCD； （2）若ADC 120,PD4,AD2，求直线 AF 与平面DEF 所成角的正弦值. 21. 数学奥林匹克竞赛是一项传统的智力竞赛项目，旨在通过竞赛选拔优秀人才，促进青少年智力发展， 很多优秀的大学在强基计划中都设置了对中学生奥林匹克竞赛成绩的要求，因此各中学学校对此十分重 视．某中学通过考试一共选拔出15名学生组成数学奥赛集训队，其中高一学生有7名、高二学生有6 名、高三学生有2名． （1）若学校随机从数学奥赛集训队抽取3人参加一项数学奥赛，求抽取的3名同学中恰有2名同学来自 高一的概率； （2）现学校欲通过考试对数学奥赛集训队成员进行考核，考试一共3道题，在测试中．3道题中至少答对 1 2 2道题记作合格．现已知张同学每道试题答对的概率均为 ，王同学每道试题答对的概率均为 ，并且每 2 3 位同学回答每道试题之间互不影响，记X为两名同学在考试过程中合格的人数，求X的分布列和数学期 望． 22. 已知函数 f x x2 ex m  ,mR ． （1）当m1时，求 f x 在点A1,e1 处的切线方程． f x （2）若gx lnx1的图象恒在x轴上方，求实数m的取值范围． x 第5页/共7页第6页/共7页第7页/共7页莆田锦江中学 2023-2024 学年上学期期中考试 高三数学 一、单选题   A x x2 7x0 B  x x4  1. 已知集合 ， ，则AB（ ） A.  B. 4,7 C. 0, D. 0,4 【答案】C 【解析】 【分析】先将集合A化简，再根据集合的并集运算得解. 【详解】因为A  x x2 7x0    x 0 x7  ，B  x x4  ， 故A  B0, . 故选：C． 2. 已知 p:x2 x0，那么命题 p的一个必要不充分条件是 （ ） 1 2 1 A. 0 x1 B. 1 x1 C.  x D.  x2 2 3 2 【答案】B 【解析】 【分析】根据必要条件的定义对每个选择进行分析即可求解． 【详解】 p:x2 x00 x1， 根据充分条件、必要条件的定义可知： 对于A，0 x1是 p的充要条件,A错误； 对于B，1 x1是 p的必要不充分条件，B正确； 1 2 对于C，  x 是 p的充分不必要条件，C错误； 2 3 1 对于D，  x2是 p的既不充分也不必要条件，D错误． 2 故选:B． 3. 命题“x1，sinxx2 1”的否定是（ ） A. x1，sinxx2 1 B. x1，sinxx2 1 第1页/共20页C. x1，sinxx2 1 D. x1，sinxx2 1 【答案】B 【解析】 【分析】根据全称量词命题的否定为存在量词命题得出结果. 【详解】因为全称量词命题的否定为存在量词命题， 故“x1，sinxx2 1”的否定是“x1，sinxx2 1”， 故选：B． x2 1 4. 函数 f x 的图象大致为（ ） x A. B. C. D. 【答案】D 【解析】 【分析】根据函数的奇偶性可排除BC,根据单调性可判断A，即可求解. x2 1 (x)2 1 x2 1 【详解】 f x 的定义域是  x x0  ，关于原点对称， f(x)   f x ，所以 x x x f x 是偶函数，排除B，C； x2 1 1 当x0时， f(x)  x ，易知 f x 在 0, 上是增函数，排除A． x x 故选：D 5. 已知函数 f x 的导函数为 f x ，若 f x2xf1lnx，则 f1（ ） A. 1 B. 1 C. 2 D. 2 【答案】A 第2页/共20页【解析】 1 【分析】求得 fx2f1 ，令x1，即可求解. x 1 【详解】由函数 f x2xf1lnx，可得 fx2f1 ， x 令x1，可得 f12f11，解得 f11. 故选：A. π  6. 已知  ,π ，且3cos24sin1，则tan2（ ） 2  1 4 2 A. B. 3 7 1 4 2 C.  D.  3 7 【答案】D 【解析】 1 【分析】由倍角余弦公式并整理得3sin22sin10，结合角的范围得sin ，进而求tan， 3 应用倍角正切公式求值即可. 【详解】由3cos24sin36sin24sin1，即 3sin22sin1(3sin1)(sin1)0， 1 π  1 所以sin 或sin1，又  ,π ，则sin ， 3 2  3 2 2 1 所以cos ，则tan ， 3 2 2 2tan 4 2 由tan2  . 1tan2 7 故选：D 7. 第19届亚运会将于2023年9月23日至10月8日在杭州举行，甲､乙等4名杭州亚运会志愿者到游泳､ 射击､体操三个场地进行志愿服务，每名志愿者只去一个场地，每个场地至少一名志愿者，若甲不去游泳 场地，则不同的安排方法共有（ ） A. 12种 B. 18种 C. 24种 D. 36种 【答案】C 第3页/共20页【解析】 【分析】本题只需考虑游泳场有2名志愿者和1名志愿者两种情况即可. 【详解】①游泳场地安排2人，则不同的安排方法有C2A2 6种， 3 2 ②游泳场地只安排1人，则不同的安排方法有C1C2A2 18种， 3 3 2 所以不同的安排方法有61824种. 故选：C 8. 数学来源于生活，约3000年以前，我国人民就创造出了属于自己的计数方法．十进制的算筹计数法就是 中国数学史上一个伟大的创造，算筹实际上是一根根同长短的小木棍．下图是利用算筹表示数1～9的一种 方法．例如：3可表示为“”，26可表示为“ ”，现有5根算筹，据此表示方法，若算筹不能剩余，则用 1～9这9个数字表示的所有两位数中，个位数与十位数之和为5的概率是（ ） 1 5 7 1 A. B. C. D. 3 12 2 12 【答案】A 【解析】 【分析】根据题意把5根算筹所能表示的两位数列举出来后，求出数字和为5的两位数个数作答. 【详解】1根算筹只能表示1，2根算筹可表示2和6，3根算筹可表示3和7，4根算筹可表示4和8，5 根算筹可表示5和9， 因此5根算筹表示的两位数有14，18，41，81，23，27，32，72，63，67，36，76，共12个， 其中个位数与十位数之和为5的有14，41，23，32，共4个， 4 1 所以所求概率为P  ． 12 3 故选：A 二、多选题 1x 9. 关于函数 f xln ，下列选项中正确的有（ ） 1x A. f x 的定义域为 ,1U1, B. f x 为奇函数 C. f x 在定义域上是增函数 第4页/共20页D. 函数 f x 与y ln1xln1x 是同一个函数 【答案】BD 【解析】 1x 【分析】①求函数 f x 的定义域,可令 0,解出此不等式的解集即可得到所求函数的定义域； 1x ②判断函数的奇偶性,要用定义法,由函数解析式研究 f x 与 f x 的关系,即可证明出函数的性质； ③此函数是一个减函数,由定义法证明要先任取x,x 且x  x ,再两函数值作差,判断差的符号,再由定义得 1 2 1 2 出结论. ④判断函数事都是同一函数,首先看定义域,定义域相同,然后看解析式,解析式也相同,即为同一函数. 1x 【详解】①由题意令 0,解得1 x1,所以数的定义域是(1,1),A错误； 1x 1+x 1- x ②由A知函数的定义域(1,1)关于原点对称,且 f (- x) =ln =- ln =- f(x)函数是奇函数,B正 1- x 1+x 确； ③此函数在定义域上是减函数,证明如下：任取x,x 属于(1,1)且x  x , 1 2 1 2 1- x 1- x (1- x )(1+x ) f (x )- f (x ) =ln 1 - ln 2 =ln 1 2 , 1 2 1+x 1+x (1- x )(1+x ) 1 2 2 1 由于x,x 属于(1,1)且x  x , 1 2 1 2 1x 1x 0 1x 1x 0, 1 2 , 2 1 1x 1x  可得 1 2 1 1x 1x  2 1 (1- x )(1+x ) 所以ln 1 2 >0, (1- x )(1+x ) 2 1 即有 f x  f x 0,即 f x  f x  , 1 2 1 2 故函数在定义域是减函数,C错误； 1x0 ④函数y ln1xln1x 定义域： ,即(1,1), 1x0 1x y ln1xln1xln  f x , 1x 第5页/共20页故函数 f x 与y ln1xln1x 是同一个函数,D正确. 故选BD 【点睛】本题考查函数的基本性质：定义域、奇偶性、单调性,只需按照定义判断即可. π 10. 已知函数 f x 的图象是由函数y 2sinxcosx的图象向右平移 个单位得到，则（ ） 6 A. f x 的最小正周期为π  π π B. f x 在区间   ,  上单调递增  6 3 π C. f x 的图象关于直线x 对称 3 π  D. f x 的图象关于点 ,0 对称 6  【答案】AD 【解析】  π 【分析】用二倍角公式化简y 2sinxcosx，向右平移后得 f xsin  2x ，分别代入正弦函数的单  3 调区间，对称轴，对称中心分别对四个选项判断即可. π  π  π 【详解】因为y 2sinxcosxsin2x，向右平移 个单位得 f xsin2  x  sin  2x ，则 6  6  3 2π 最小正周期为T  π，故A选项正确； 2 π π π π 5π 令 2kπ2x  2kπ，解得 kπ x kπ，所以单调递增区间为 2 3 2 12 12  π 5π    kπ, kπ  ,kZ，故B选项错误；  12 12  π π 5π kπ 令2x  kπ,解得x  ,kZ，故C选项错误； 3 2 12 2 π π π  令2x kπ,解得x kπ,kZ所以函数 f x 的对称中心为 kπ,0  ,kZ，故D选项正确. 3 6 6  故选：AD 11. 如图，在底面为正方形的四棱锥PABCD中，PA平面ABCD，AP AB1，则下列说法正确 的是（ ） 第6页/共20页A. 异面直线PB与AC所成的角为60 B. 直线PD与平面PAC 所成的角为30 C. 平面PBD与平面PAB的夹角为30 3 D. 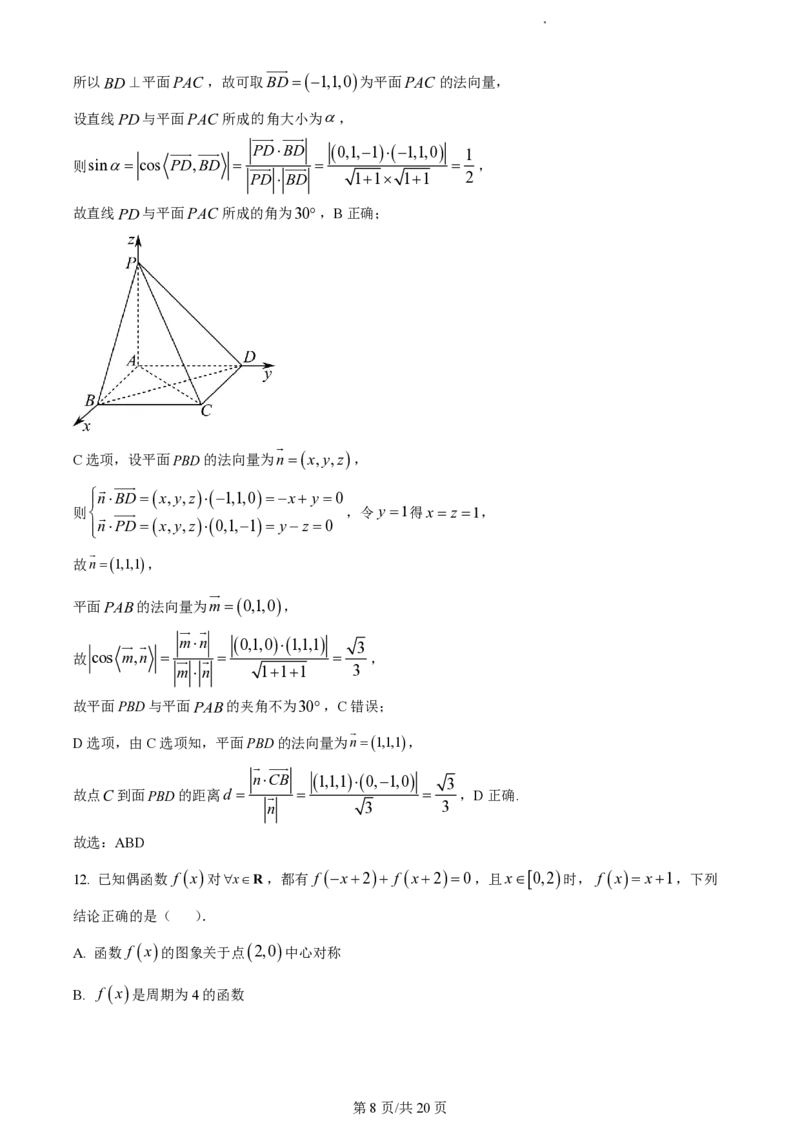点C到面PBD的距离为 3 【答案】ABD 【解析】 【分析】A选项，证明AB,AD,PA两两垂直，建立空间直角坐标系，利用异面直线夹角余弦公式进行求  解；B选项，证明BD⊥平面PAC ，故可取BD1,1,0为平面PAC 的法向量，利用线面角的向量求 解公式进行求解；C选项，求出两平面的法向量，利用相关公式求出两平面夹角；D选项，利用点到平面 的距离公式求出答案. 【详解】A选项，因为PA平面ABCD，AB,AD平面ABCD， 所以PA AB，PA AD， 又四边形ABCD为正方形，故AB,AD,PA两两垂直， 以A为坐标原点，AB,AD,AP所在直线分别为x,y,z轴，建立空间直角坐标系， 则P0,0,1,B1,0,0,A0,0,0,C1,1,0,D0,1,0 ，   则PB1,0,1,AC 1,1,0，     PBAC 1,0,11,1,0 1 设直线PB与AC所成的角大小为，则cos cos PB,AC      ， PB  AC 11 11 2 故=60，A正确； B选项，因为四边形ABCD为正方形，所以AC⊥BD， 又PA平面ABCD，BD平面ABCD，故PA BD， 因为ACPA A，AC,PA平面PAC ， 第7页/共20页 所以BD⊥平面PAC ，故可取BD1,1,0为平面PAC 的法向量， 设直线PD与平面PAC 所成的角大小为，     PDBD 0,1,11,1,0 1 则sin cos PD,BD    ，   PD  BD 11 11 2 故直线PD与平面PAC 所成的角为30，B正确；  C选项，设平面PBD的法向量为nx,y,z，   n  BDx,y,z1,1,0x y 0 则  ，令y 1得x z 1，  n  PDx,y,z0,1,1 yz 0  故n1,1,1，  平面PAB的法向量为m0,1,0，     mn 0,1,01,1,1 3 故 cos m,n    ，   m  n 111 3 故平面PBD与平面PAB的夹角不为30，C错误；  D选项，由C选项知，平面PBD的法向量为n1,1,1，   nCB 1,1,10,1,0 3 故点C到面PBD的距离d     ，D正确. n 3 3 故选：ABD 12. 已知偶函数 f x 对xR，都有 f x2 f x20，且x0,2 时， f x x1，下列 结论正确的是（ ）． A. 函数 f x 的图象关于点 2,0 中心对称 B. f x 是周期为4的函数 第8页/共20页C. f 20 13 5 D. f     2  2 【答案】ACD 【解析】 【分析】由 f x2 f x20可推出函数 f x 的对称中心即可判断A项，根据 f x 为偶函数及 f x f x20可推出函数 f x 的周期可判断B项，采用赋值法、偶函数性质、周期性即可判断C 项、D项. 【详解】对于A项，由 f x2 f x20得 f x 的图象关于 2,0 中心对称，故A正确； 对于B项，因为 f x 为偶函数，所以 f x2 f x2 ， 又因为 f x2 f x20，所以 f x2f x2 ， 所以 f xf x4 ， 所以 f x8f x4 f x ，即 f x 是周期为8的函数，故B项错误； 对于C项，因为 f x2f x2 ， 所以令x0，则 f 2f 2 ，即 f 20， 又因为 f x 为偶函数，所以 f 2 f 20，故C项正确； 对于D项，因为x0,2 时， f x x1， f x 的周期为8， f x 为偶函数， 13  3 3 5 所以 f    f     f    ，故D项正确．  2   2 2 2 故选：ACD． 三、填空题 13. 某工厂月产品的总成本y（单位：万元）与月长量x（单位：万件）有如下一组数据，从散点图分析可 知y与x线性相关．如果回归方程是y  x3.5，那么表格中数据a的值为______． x/万件 1 2 3 4 y/万件 3.8 5.6 a 8.2 第9页/共20页32 【答案】6.4## 5 【解析】 【分析】分别求出工厂总成本和月长量的平均值，代入回归方程，即可求出表格中数据a的值. 【详解】由题意及表知， 1234 5 1 17.6a x  ，y  3.85.6a8.2 ， 4 2 4 4 ∵回归方程是y  x3.5， 17.6a ∴ 2.53.5， 4 ∴a 6.4． 故答案为：6.4. 10  1 14.  x  的二项展开式中，x2项的系数为__________．  x 【答案】210 【解析】 【分析】先求出二项式展开式的通项公式，然后令x的次数为2，求出r，代入通项公式中可求得结果. 10 r  1 1 【详解】 x 的二项展开式的通项公式为T Cr x10r  Cr x102r，      x r1 10  x 10 令102r2，得r 4， 所以x2项的系数为C4 210， 10 故答案为：210 3π 3  π 15. 若π 且sinθ  ，则tan    ______． 2 5  4 1 【答案】 7 【解析】 【分析】先根据平方关系及商数关系求出cos,tan，再利用两角差的正切公式即可得解. 3π 3 4 【详解】因为π 且sinθ  ，所以cos 1sin2 ， 2 5 5 3 所以tan ， 4 第10页/共20页π 3 tantan 1  π 4 4 1 则tan       .  4 π 3 7 1tantan 1 4 4 1 故答案为： . 7 16. 我们将服从二项分布的随机变量称为二项随机变量，服从正态分布的随机变量称为正态随机变量.概率 论中有一个重要的结论是棣莫弗—拉普拉斯极限定理，它表明，若随机变量Y ~ Bn,p ，当n充分大 时，二项随机变量Y 可以由正态随机变量X 来近似，且正态随机变量X 的期望和方差与二项随机变量Y 1 的期望和方差相同.棣莫弗在1733年证明了P 的特殊情形.1812年，拉普拉斯对一般的P进行了证明. 2 现抛掷一枚质地均匀的硬币100次，则利用正态分布近似估算硬币正面向上次数不超过60次的概率为 ______. （附：若X  N  ,2 ，则P X 0.683，P2 X 20.954， P3 X 30.997） 【答案】0.977 【解析】 【分析】利用二项分布的期望和方差的公式以及正态分布的3原则求解即可.  1 【详解】抛掷一枚质地均匀的硬币100次，设硬币正面朝上次数为X ,则X  B  100, ,  2 1 1  1 故EX100 50， DX100   1  25， 2 2  2 由已知得X  N  ,2 ，且 EX 50,2  DX  25, 因为P40 X 600.954， 所以P40 X 601PX 40PX 60 12PX 60 解得PX 600.023， , 所以PX 601PX 6010.0230.977, 故答案为：0.977. 四、解答题  π  π 17. 已知函数 f xsin  2x  sin  2x   3cos2x.  3  3 （1）求函数 f(x)的最小正周期； 第11页/共20页 π （2）当x  0,  时，求函数 f(x)的单调递减区间和值域.  2 【答案】（1）π  π π （2） f(x)的减区间为  ,  ；函数 f(x)的值域为   3,2  12 2 【解析】 π 【分析】（1）化简得 f(x)2sin(2x )，从而利用周期公式即可求解； 3 π π 3π  π （2）令 2kπ2x  2kπ,kZ，求解并结合x  0,  即可求得单调减区间；由于 2 3 2  2  π π π 4π x  0,  ，可得2x   ,  ，再结合正弦函数的性质即可求解.  2 3 3 3  【小问1详解】 π 1 3 π 1 3 因为sin(2x ) sin2x cos2x，sin(2x ) sin2x cos2x， 3 2 2 3 2 2 π 所以 f(x)sin2x 3cos2x2sin(2x )， 3 2π 所以 f(x)的最小正周期是 =π； 2 【小问2详解】 π π 3π π 7π 令 2kπ2x  2kπ,kZ，解得 kπ x kπ,kZ， 2 3 2 12 12 π 7π 令k 0，则  x 12 12  π  π π 由于x  0,  ，所以 f(x)的减区间为  , .  2 12 2  π π π 4π  π  3  因为x  0,  ，则2x   ,  ，所以sin  2x   ,1，  2 3 3 3   3  2   π 所以2sin  2x     3,2  ，即函数 f(x)的值域为   3,2  . 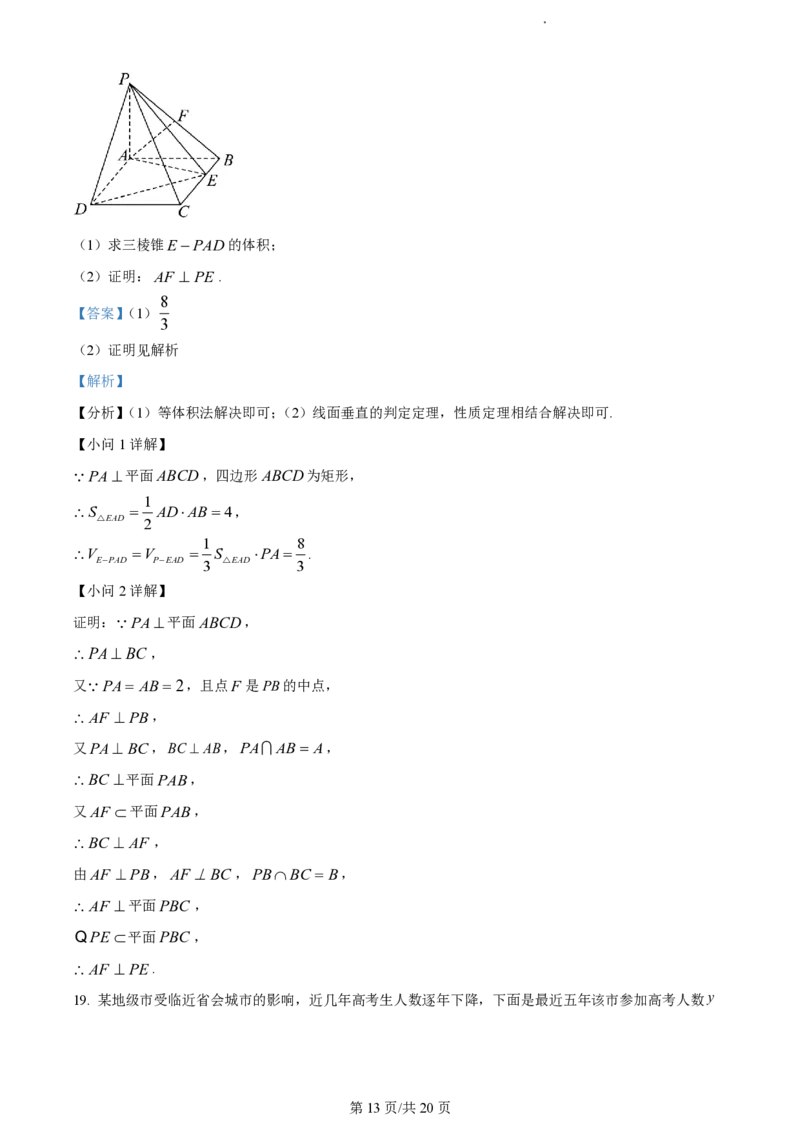 3 18. 如图，PA平面ABCD，四边形ABCD为矩形，PA AB2，AD4，点F 是PB的中点，点 E在边BC上移动. 第12页/共20页（1）求三棱锥EPAD的体积； （2）证明：AF  PE. 8 【答案】（1） 3 （2）证明见解析 【解析】 【分析】（1）等体积法解决即可；（2）线面垂直的判定定理，性质定理相结合解决即可. 【小问1详解】 PA平面ABCD，四边形ABCD为矩形，  1 S  ADAB4， △EAD 2 1 8 V V  S PA . EPAD PEAD 3 △EAD 3 【小问2详解】 证明： PA平面ABCD，  PA BC， 又 PA AB2，且点F 是PB的中点，  AF  PB， 又PA BC，BC AB，PA AB A，  BC 平面PAB， 又AF 平面PAB， BC  AF ， 由AF  PB，AFBC ，PBBC  B， AF 平面PBC ， QPE 平面PBC ， AF  PE. 19. 某地级市受临近省会城市的影响，近几年高考生人数逐年下降，下面是最近五年该市参加高考人数y 第13页/共20页与年份代号x之间的关系统计表. 年份代号x 1 2 3 4 5 高考人数y（千人） 35 33 28 29 25 （其中2018年代号为1，2019年代号为2，…2022年代号为5） （1）求y关于x的线性回归方程； （2）根据（1）的结果预测该市2023年参加高考的人数； （3）试分析该市参加高考人数逐年减少的原因. n  x x  y  y  i i （参考公式：b i1 ,a ybx）  n  x x 2 i i1 【答案】（1）y 2.4x37.2 （2）22.8千人 （3）答案见解析 【解析】 【分析】（1）根据题中数据计算得b2.4,a37.2即可解决；（2）根据（1）中回归方程计算即可；（3） 言之有理，客观分析即可. 【小问1详解】 设回归方程为y bxa，由表中数据知， x3，y 30. 25(1)30(2)1(1)2(5) 12 所以b  2.4， 4141 5 所以a  ybx302.4337.2， 所以y关于x的回归方程y 2.4x37.2. 【小问2详解】 由（1）得y关于x的回归方程y 2.4x37.2. 令x6，y 2.4637.222.8（千人）， 所以预测该市2023年参加高考的人数为22.8千人. 【小问3详解】 ①该市经济发展速度慢； ②该市人口数量减少； 第14页/共20页③到省会城市求学人数增多. 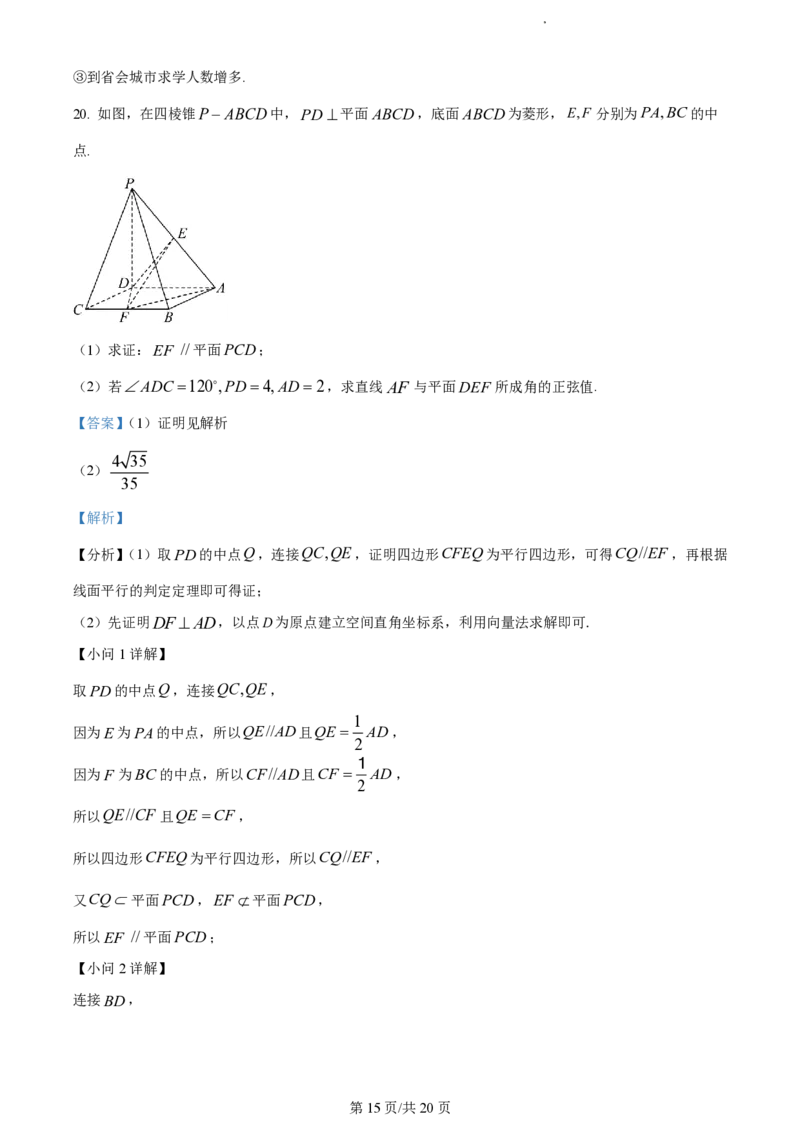20. 如图，在四棱锥PABCD中，PD 平面ABCD，底面ABCD为菱形，E,F 分别为PA,BC的中 点. （1）求证：EF //平面PCD； （2）若ADC 120,PD4,AD2，求直线 AF 与平面DEF 所成角的正弦值. 【答案】（1）证明见解析 4 35 （2） 35 【解析】 【分析】（1）取PD的中点Q，连接QC,QE，证明四边形CFEQ为平行四边形，可得CQ//EF，再根据 线面平行的判定定理即可得证； （2）先证明DFAD，以点D为原点建立空间直角坐标系，利用向量法求解即可. 【小问1详解】 取PD的中点Q，连接QC,QE， 1 因为E为PA的中点，所以QE//AD且QE  AD， 2 1 因为F 为BC的中点，所以CF//AD且CF  AD， 2 所以QE//CF 且QE CF， 所以四边形CFEQ为平行四边形，所以CQ//EF， 又CQ平面PCD，EF 平面PCD， 所以EF //平面PCD； 【小问2详解】 连接BD， 第15页/共20页在菱形ABCD中，ADC 120，则ABC 60， 所以△ABD和△CBD都是等边三角形， 因为F 为BC的中点，所以DF  BC,DF  3， 因为AD//BC，所以DFAD， 如图，以点D为原点建立空间直角坐标系，   则A0,2,0,D0,0,0,E0,1,2,F 3,0,0 ，        所以DE 0,1,2,DF  3,0,0 ,AF  3,2,0 ，  设平面DEF 的法向量为nx,y,z，   n  DE  y2z 0  则有 ，可取n0,2,1，   nDF  3x0     nAF 4 4 35 cos n,AF    则   ， n AF 5 7 35 4 35 所以直线 AF 与平面DEF 所成角的正弦值为 . 35 21. 数学奥林匹克竞赛是一项传统的智力竞赛项目，旨在通过竞赛选拔优秀人才，促进青少年智力发展， 很多优秀的大学在强基计划中都设置了对中学生奥林匹克竞赛成绩的要求，因此各中学学校对此十分重 视．某中学通过考试一共选拔出15名学生组成数学奥赛集训队，其中高一学生有7名、高二学生有6 名、高三学生有2名． （1）若学校随机从数学奥赛集训队抽取3人参加一项数学奥赛，求抽取的3名同学中恰有2名同学来自 高一的概率； （2）现学校欲通过考试对数学奥赛集训队成员进行考核，考试一共3道题，在测试中．3道题中至少答对 1 2 2道题记作合格．现已知张同学每道试题答对的概率均为 ，王同学每道试题答对的概率均为 ，并且每 2 3 位同学回答每道试题之间互不影响，记X为两名同学在考试过程中合格的人数，求X的分布列和数学期 第16页/共20页望． 24 【答案】（1） 65 67 （2）分布列见解析，EX 54 【解析】 【分析】（1）利用组合数及古典概型求解； （2）分别计算两位同学合格的概率，再计算合格人数的概率，列出分布列，计算期望即可. 【小问1详解】 设事件A为“抽取的3名同学中恰有2名同学来自高一”， C2C1 24 则有PA 7 8  ． C3 65 15 【小问2详解】 设张同学、王同学答对的题数分别为Y，Z， 张同学在考试中合格的概率为： 2 1 3 0 1 1 1 1 1 PY 2 PY 2PY 3C2  C3   ，         3 2 2 3 2 2 2 王同学在考试中合格的概率为： 2 1 3 0 2 1 2 1 20 PZ 2 PZ 2PZ 3C2  C3   ．         3 3 3 3 3 3 27 由题意得X可取0，1，2，  1  20 7 则PX 0  1    1   ，  2  27 54 1  20  1 20 1 PX 1   1    1    ， 2  27  2 27 2 1 20 10 PX 2   ， 2 27 27 所以X的分布列为 X 0 1 2 7 10 1 P 54 2 27 7 1 10 67 因此X的数学期望EX0 1 2  ． 54 2 27 54 第17页/共20页22. 已知函数 f x x2 ex m  ,mR ． （1）当m1时，求 f x 在点A1,e1 处的切线方程． f x （2）若gx lnx1的图象恒在x轴上方，求实数m的取值范围． x 【答案】（1） 3e2x y2e10 （2）m1 【解析】 【分析】（1）由题意，将m1代入函数 f x 的解析式中，对函数 f x 进行求导，得到 f1 和 f 1 ， 代入切线方程中即可求解； lnx1 lnx1 （2）将函数gx 的图像恒在x轴上方，转化成m ex恒成立，构造函数x ex， x x 此时问题转化成函数最值问题，对函数x 进行求导，利用导数的几何意义以及零点存在性定理进行求解 即可． 【小问1详解】 f x x2 ex 1    fx  x2 2x  ex 2x  f13e2． 又 f 1e1 \ f (x)在点A1,e1 处的切线方程为 3e2x y2e10 【小问2详解】 f x gx lnx1的图像恒在x轴上方，等价于x  ex m  lnx10恒成立 x lnx1 即m ex恒成立， x lnx1 lnx lnxx2ex 令x ex，则x ex  x x2 x2 令gx  lnxexx2 ，则gx   1 x2ex 2xex   0  x  第18页/共20页所以gx 在 0, 上单调递减 1 又g   0,g10，所以在 0, 上存在唯一的x 使gx 0 2 0 0 当x0,x  时x0,x 单调递增，当xx ,时x0,x 单调递减． 0 0 lnx 1 故x 的最大值为x  0 ex 0 0 x 0 lnx 又1nx ex 0x 2 0，故x ex 0  0 ， 0 0 0 x 0 两边取对数得lnx  x lnlnx lnx  0 0 0 0 1 又hx xlnx在定义域内单调递增，所以x lnx ，故ex 0  0 0 x 0 lnx 1 lnx 1 1 所以x  0 ex 0  0   1 0 x x x x 0 0 0 0 所以m1. 【点睛】方法点睛：含参不等式恒成立求参数值(取值范围)常用的方法： （1）直接法：直接求导确定函数的单调性得到最值，再通过解不等式确定参数范围； （2）分离参数法：先将参数分离，转化成求函数的最值问题加以解决； （3）数形结合法：先对解析式变形，进而构造两个函数，然后在同一平面直角坐标系中画出函数的图 象，利用数形结合的方法求解. 第19页/共20页第20页/共20页