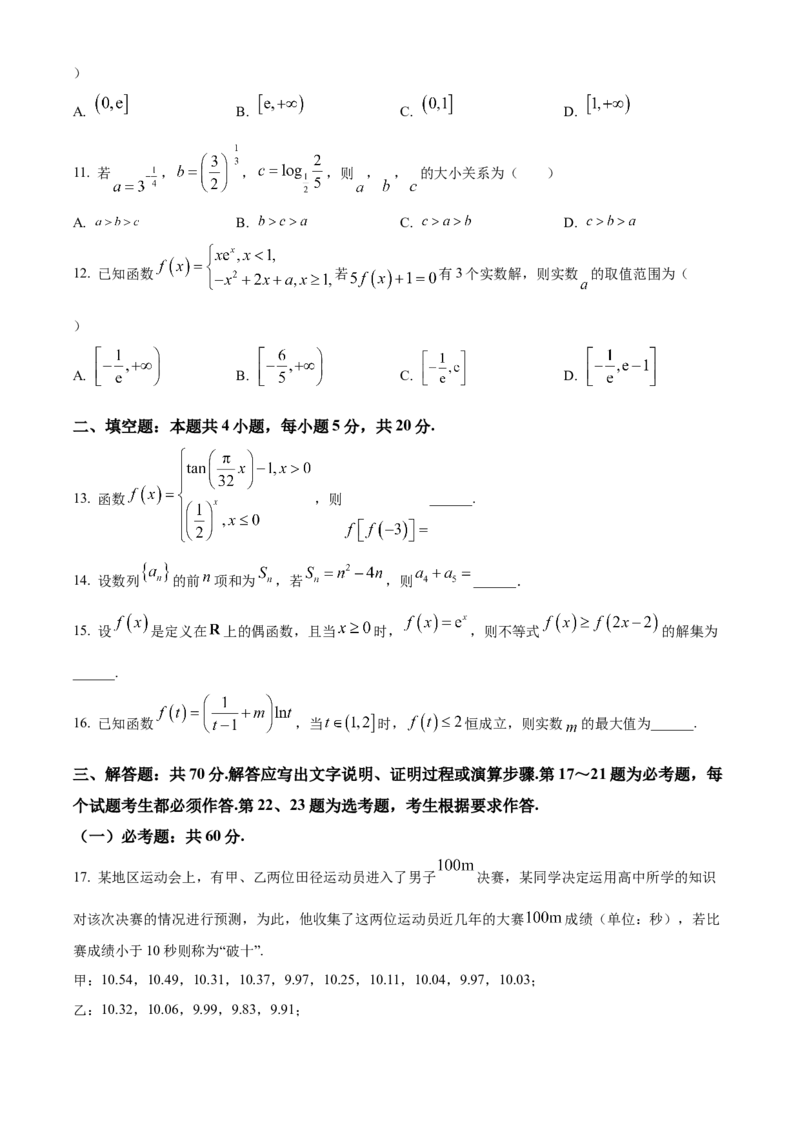文档内容
2024 届高三第一次联考
文科数学
考试时间120分钟,满分150分
注意事项:
1.答题前,考生务必在答题卡上将自己的姓名、座位号和考籍号用0.5毫米的黑色签字笔填写
清楚,考生考试条形码由监考老师粘贴在答题卡上的“贴条形码区”.
2.选择题使用2B铅笔填涂在答题卡上对应题目标号的位置上,如需改动,用橡皮擦擦干净后
再填涂其它答案;非选择题用0.5毫米的黑色签字笔在答题卡的对应区域内作答,超出答题
区域答题的答案无效;在草稿纸上、试卷上答题无效.
3.考试结束后由监考老师将答题卡收回.
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项
是符合题目要求的.
1. 已知集合 , ,全集 ,则 ( )
.
A B.
.
C D.
2. 已知幂函数 的图象过点 ,则 ( )
A. B. 1 C. 2 D. 3
3. 已知 为复数单位, ,则 的模为( )
A. B. 1 C. 2 D. 4
4. 在 中,“ ”是“ 为锐角三角形”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
5. 在等比数列 中, , 是方程 两根,若 ,则m的值为( )A. 3 B. 9 C. D.
6. 已知 , , , ,若存在非零实数 使得 ,则 的最小值为
( )
.
A 8 B. 9 C. 10 D. 12
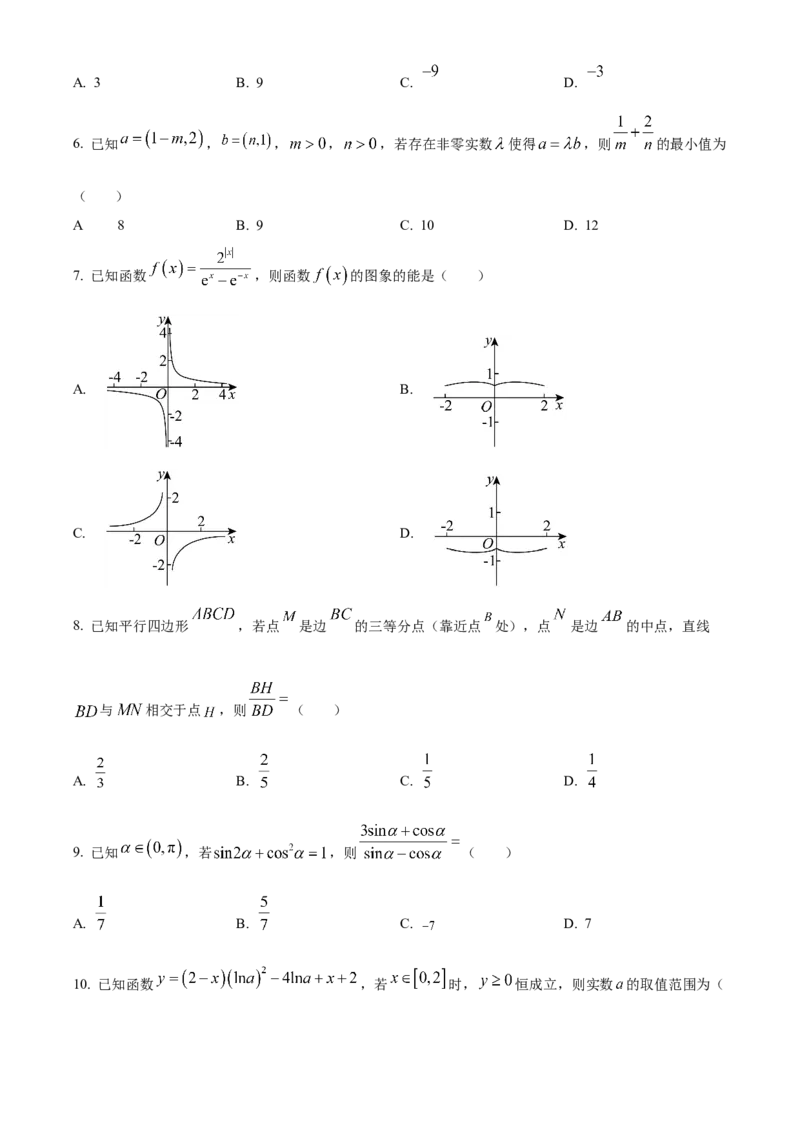
7. 已知函数 ,则函数 的图象的能是( )
A. B.
C. D.
8. 已知平行四边形 ,若点 是边 的三等分点(靠近点 处),点 是边 的中点,直线
与 相交于点 ,则 ( )
A. B. C. D.
9. 已知 ,若 ,则 ( )
A. B. C. D. 7
10. 已知函数 ,若 时, 恒成立,则实数 的取值范围为()
A. B. C. D.
11. 若 , , ,则 , , 的大小关系为( )
A. B. C. D.
12. 已知函数 若 有3个实数解,则实数 的取值范围为(
)
A. B. C. D.
二、填空题:本题共4小题,每小题5分,共20分.
13. 函数 ,则 ______.
14. 设数列 的前 项和为 ,若 ,则 ______.
15. 设 是定义在 上的偶函数,且当 时, ,则不等式 的解集为
______.
16. 已知函数 ,当 时, 恒成立,则实数 的最大值为______.
三、解答题:共70分.解答应㝍出文字说明、证明过程或演算步骤.第17~21题为必考题,每
个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.
(一)必考题:共60分.
17. 某地区运动会上,有甲、乙两位田径运动员进入了男子 决赛,某同学决定运用高中所学的知识
对该次决赛的情况进行预测,为此,他收集了这两位运动员近几年的大赛 成绩(单位:秒),若比
赛成绩小于10秒则称为“破十”.
甲:10.54,10.49,10.31,10.37,9.97,10.25,10.11,10.04,9.97,10.03;
乙:10.32,10.06,9.99,9.83,9.91;(1)求甲成绩的中位数与平均数(平均数的结果保留3位小数);
(2)从乙的5次成绩中任选3次,求恰有2次成绩“破十”的概率.
18. 已知 的内角A,B,C所对的边分别为a,b,c,且 .
(1)求角B;
(2)若边 上的中线 长为2,求 面积的最大值.
19. 如图,在直三棱柱 中,底面 是以 为底边的等腰直角三角形, ,
.
(1)求证:平面 平面 ;
(2)求点 到平面 的距离.
20. 已知椭圆 的左、右焦点分别为 , ,短半轴 长为1,点 在椭圆 上
运动,且 的面积最大值为 .
(1)求椭圆 的方程;
(2)当点 为椭圆 的上顶点时,设过点 的直线 交椭圆 于 , 两点,直线 ,
的斜率分别为 , ,求证: 为定值.
21. 已知函数 , .
(1)当 时,求 在 处的切线方程;(2)当 时,设函数 ,求证: 有解.
(二)选考题:共10分.请考生在22、23题中任选一题作答,如果多做,则按所做的第一题
计分.
选修4-4:坐标系与参数方程
22. 在直角坐标系中,直线 的参数方程为 ( 为参数),曲线 的参数方程为
( 为参数).
(1)求直线 和曲线 的直角坐标方程;
(2)若直线 与曲线 相交弦的中点坐标为 ,求直线 的极坐标方程.
选修4-5:不等式选讲
23. 已知定义域为 的函数 .
(1)若 ,求函数 的最小值;
的
(2)若 ,不等式 恒成立,求实数 最小值.