文档内容
济南市 2026 届高三第一次模拟考试
数 学 试 题
本试卷共4页,19题,全卷满分150分。考试用时120分钟。
注意事项:
1.答卷前,考生务必将自己的姓名、考生号、考场号、座位号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改
动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写在本试
卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、单项选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项
是符合题目要求的。
1.设集合A={x|00)的左、右焦点分别为F₁,F₂,A 是C 的左顶点,P 为C 所
a2 b2
在平面内一点,且∠F₃F₂P=60°.若△PF₁F₂与△PF₁A 均为等腰三角形,则C的离心率为
1
3
8.若存在a>0,对任意的x∈(0,+∞),都有 xlnx+2a≥ax+b,!,则b的最大值为
1
A.− B.ξ₂ C.2ln2 D.1+ln2
e
二、多项选择题:本题共3小题,每小题6分,共18分。在每小题给出的四个选项中,有多项符
合题目要求。全部选对的得6分,部分选对的得部分分,有选错的得0分。
9.已知实数a,b,c 满足a0)的实轴长为4,且经过点 P(3, ).
a2 b2 2
(1)求C 的方程;
(2)记C的右顶点为A,点R 在线段AP(不含端点)上运动,垂直于x 轴的直线RM 交C于点
M(x ,y )(M在第一象限),点S 满足 ⃗MR=⃗RS,设直线 AS 与C 的另一个交点为N(x₂,y₂).
1 1
(i)用x₁,y₁表示直线AS 的斜率k₀;
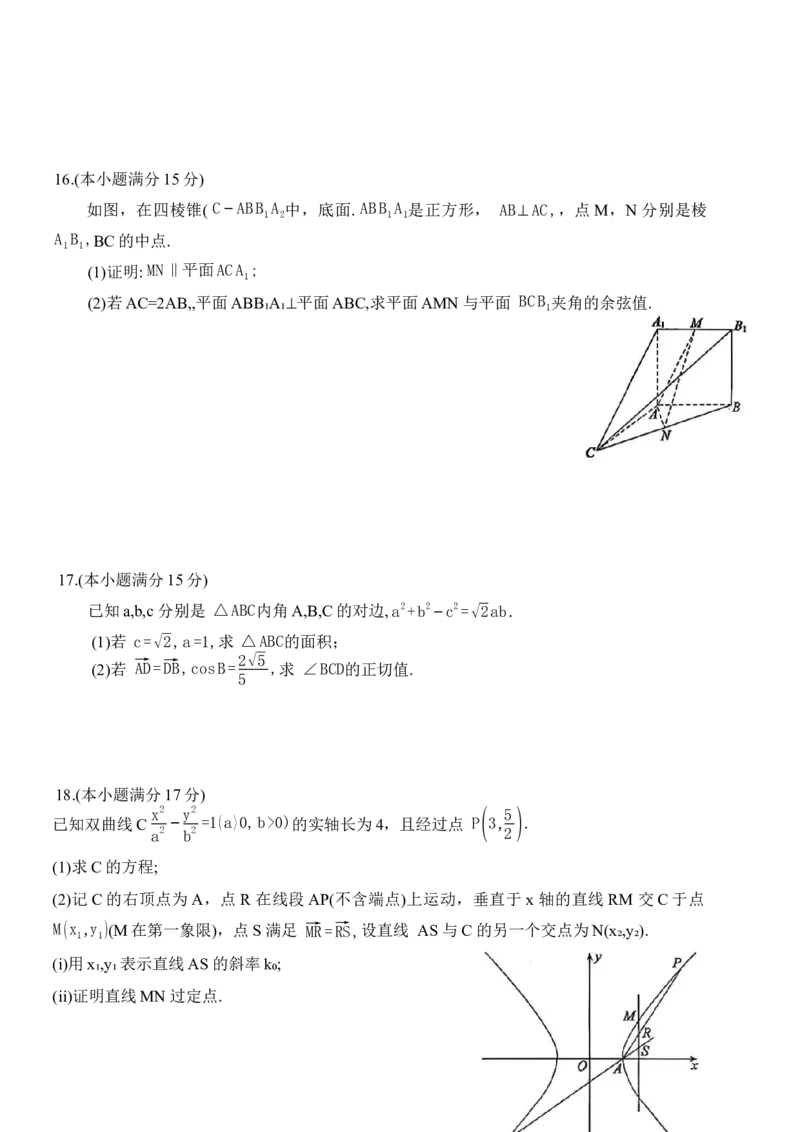
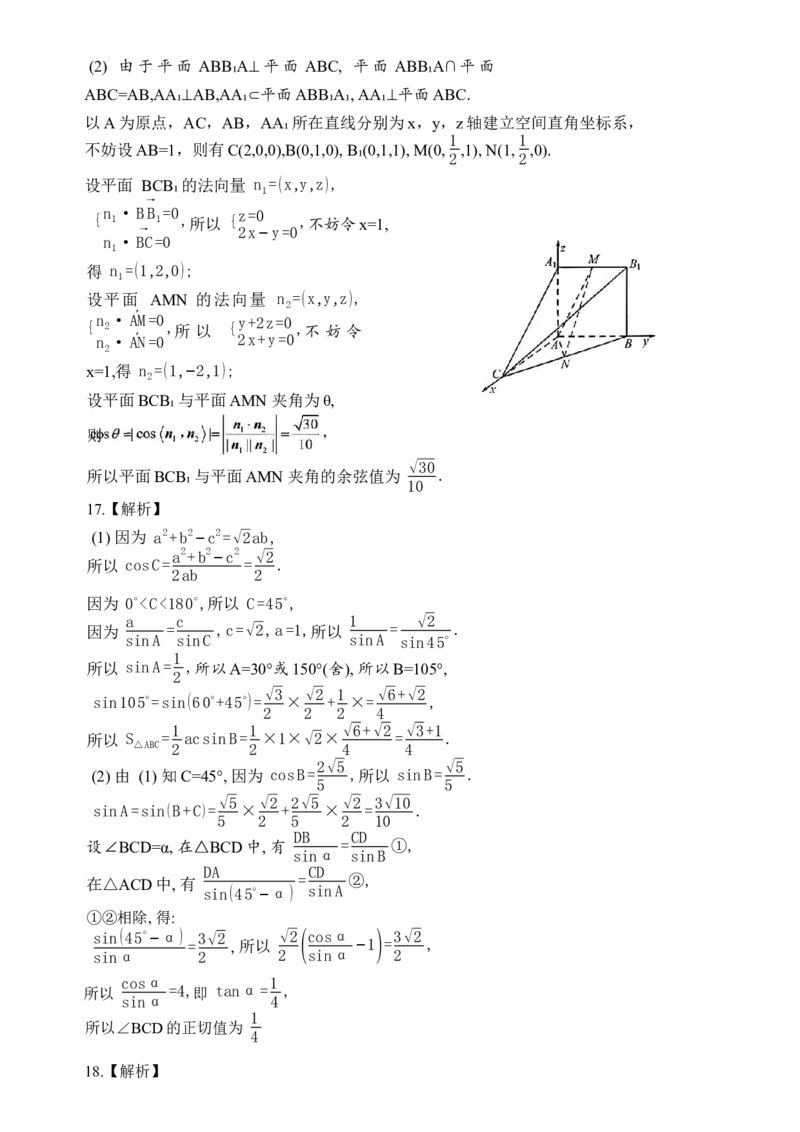
(ii)证明直线MN 过定点.19.(本小题满分17分)
sinx
已知函数f(x)的定义域为(0,+∞),导函数 f' (x)= .将f(x)所有的极值点按照从小到
x
大的顺序排列构成数列( {x },n∈N∗.
n
(1)若 x∈(x ,x ),比较|f'(x)|与| f' (2x −x)∣的大小;
n n+1 n+1
(2)从下列两个命题中任选一个证明:
①数列 {f(x )}为递减数列;②数列 {f(x )}为递增数列;
2n−1 n
(若两个命题均选,按照第一个解答计分)
(3)若k 为正整数,且对任意的 x ,x ∈[π,+∞),都有 ∣f(x )−f(x )∣0,
1 2 5−4k2 1 2 5−4k2
y y kx +m kx +m 2kx x +(m−2k)(x +x )−4m 5
1 + 2 = 1 + 2 = 1 2 1 2 = =5,
x −2 x −2 x −2 x −2 x x −2(x +x )+4 m+2k
1 2 1 2 1 2 1 2
所以m=1-2k,
所以直线MN:y= kx+1-2k=k(x-2)+1,
所以直线MN过定点(2,1).
19.【解析】
sinx
(1) 令 f' (x)= =0,得x=nπ, n∈N,
x
因为x=nπ为f'(x)的变号零点, 所以. x =nπ.
n
当 x∈(x ,x )时, 2x −x>0,且sinx≠0.
n n+1 n+1
∣sin(2(n+1)π−x)| ∣sinx∣ ∣sinx∣
∣f′ (2x −x)∣=∣=∣= = ,∣f′ (x)∣= ,
n+1 |2x −x∣ 2x −x x
n+1 n+1
∣sinx∣ ∣sinx∣ 2(x −x)
∣f' (x)∣−∣f' (2x −x)∣= − =∣sinx∣ n+1 >0.
n+1 x 2x −x x(2x −x)
n+1 n+1
故 ∣f' (x)∣>∣f' (2x −x)∣.
n+1
(2) 选择①,
令 g(x)=f(x)−f(2x −x),x∈[x ,x ],
2n 2n−1 2n
则 g' (x)=f' (x)+f' (2x −x),
2n
当 x∈[x
2n−1
,x
2n
]时,即.x∈[(2n-1)π,2nπ]时, 2x
2n
−x∈[2nπ,(2n+1)π],sinx sinx
f' (x)= ≤0,f' (2x −x)=− ≥0,
x 2n 2x −x
2n
故 g' (x)=f' (x)+f' (2x −x)=−∣f' (x)∣+∣f' (2x −x)∣,
2n 2n
由(1) 知,g'(x)≤0.
故g(x)单调递减,从而有 g(x )>g(x )=f(x )−f(2x −x )=0,
2n−1 2n 2n 2n 2n
即 g(x )=f(x )−f(2x −x )=f(x )−f(x )>0,
2n−1 2n−1 2n 2n−1 2n−1 2n+1
即 f(x )>f(x ),从而数列 {f(x )}为递减数列.
2n−1 2n+1 2n−1
选择②,
令 g(x)=f(x)−f(2x −x),x∈[x ,x ],
2n+1 2n 2n+1
则 g' (x)=f' (x)+f' (2x −x),
2n+1
当 x∈[x
2n
,x
2n+1
]时, 即x∈[2nπ,(2n+1)π]时, 2x
2n+1
−x∈[(2n+1)π,(2n+2)π],
sinx sinx
f' (x)= ≥0,f' (2x −x)=− ≤0,
x 2n+1 2x −x
2n+1
故 g' (x)=f' (x)+f' (2x −x)=∣f' (x)∣−∣f' (2x −x)∣,
2n+1 2n+1
由(1) 知, g'(x)≥0,
故g(x)单调递增,从而有 g(x )