文档内容
2024 年高三年级期初调研检测
数学试题
2024.09
本试卷共 4页,19题.全卷满分 150分.考试用时 120分钟.
注意事项:
1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上,并将准考证
号条形码粘贴在答题卡上的指定位置.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需要
改动,用橡皮擦干净后,再选涂其它答案标号.回答非选择题时,将答案写在答题卡上.写在
本试卷上无效.
3.考试结束后,将本试卷和答题卡一并交回.
一、选择题:本题共 8小题,每小题 5分,共 40分.在每小题给出的四个选项中,只有一项
是符合题目要求的.
A= { x y =ln ( 4−x )} B={ 1,2,3,4,5 } AB =
1. 已知集合 , ,则 ( )
A. {5} B. {1,2,3} C. {1,2,3,4} D. {1,2,3,4,5}
【答案】B
【解析】
【分析】根据对数中真数大于0解出集合A,再利用交集含义即可得到答案.
【详解】A= { x y =ln ( 4−x )} = { x x<4 } ,则A∩B={1,2,3}.
故选:B.
2. 已知复数z满足 ( 1+2i ) z =4+3i,则z的虚部为( )
A. 1 B. −1 C. i D. −i
【答案】A
【解析】
【分析】根据复数的除法的计算公式得z =2−i,再根据共轭复数和复数虚部的概念即可.
4+3i ( 4+3i )( 1−2i ) 10−5i
【详解】z = = = =2−i,
1+2i ( 1+2i )( 1−2i ) 5
则z =2+i,则其虚部为1.
故选:A.
第1页/共21页
学科网(北京)股份有限公司π π
3. 已知命题p:∀α∈R,sin −α =cos +α ,则¬p为( )
4 4
π π π π
A. ∀α∈R,sin −α ≠cos +α B. ∃α∈R,sin −α ≠cos +α
4 4 4 4
π π π π
C. ∀α∉R,sin −α =cos +α D. ∃α∉R,sin −α =cos +α
4 4 4 4
【答案】B
【解析】
【分析】根据全称量词命题的否定,否定结论,全称变特称即可.
【详解】根据全称量词命题的否定,否定结论,全称变特称,则¬p为“∃α∈R,
π π
sin −α ≠cos +α ”.
4 4
故选:B.
4. 等差数列 的首项为−1,公差不为0,若a ,a ,a 成等比数列,则 的前6项和为( )
2 3 6
{𝑎𝑎𝑛𝑛} {𝑎𝑎𝑛𝑛}
A. −1 B. 3 C. −24 D. 24
【答案】D
【解析】
【分析】根据等比中项得到方程,解出d =2,后根据等差数列求和公式计算即可.
【详解】a ,a ,a 成等比数列,则a2 =a ⋅a ,即(a +2d)2 =(a +d)⋅(a +5d),
2 3 6 3 2 6 1 1 1
a =−1代入.得到(−1+2d)2=(−1+d)⋅(−1+5d),d ≠0,解得d =2.
1
6×5
则 { a } 的前6项和S =6×(−1)+ ×2=24.
n 6 2
故选:D.
5. 在平面直角坐标系 xOy 中,角 α 与角 β 均以 x 轴的非负半轴为始边,它们的终边关于 x 轴对称.若
1
cosα=− ,则cos (α−β)=( )
3
1 7 7
A. B. − C. 1 D.
9 9 9
【答案】B
【解析】
第2页/共21页
学科网(北京)股份有限公司【分析】运用角的终边对称性,得到正弦余弦值之间的关系,再用两角差的余弦值计算即可.
【详解】角α与角β均以x轴的非负半轴为始边,它们的终边关于x轴对称.
1 8 8
则cosα=cosβ=− ,sinα=−sinβ,且sin2α=1−cos2α= ,sinα⋅sinβ=−sin2α=− ,
3 9 9
1 8 7
故cos (α−β)=cosα⋅cosβ+sinα⋅sinβ= − =− .
9 9 9
故选:B
6. 两个粒子A,B从同一发射源发射出来,在某一时刻,它们的位移分别为S =(1,2),S =(4,3).粒子
A B
B相对粒子A的位移为S,则S在S 上的投影向量为( )
A
5 2 5 ( )
A. , B. 5,2 5 C. (1,2) D. (2,1)
5 5
【答案】C
【解析】
【分析】根据题意,求得S S S (3,1),结合向量的数量积的公式和投影向量的公式,准确计算,即
B A
可求解.
【详解】由向量S =(1,2),S =(4,3),可得粒子B相对粒子A的位移为S S S (3,1),
A B B A
可得S ⋅S =1×3+2×1=5且 S = 5 ,
A A
S ⋅S S 5
所以S 在S 上的投影向量为 A ⋅ A = ⋅(1,2)=(1,2) .
A S S 5× 5
A A
故选:C.
( x+a )2 ,x≤0
7. 设 f
(
x
)=
1 ,若 f
(
0
)
是 f
(
x
)
的最小值,则a的取值范围为( )
x+ +a,x>0
x
A.
[−1,0 ]
B.
[−1,2 ]
C.
[−2,−1 ]
D.
[−2,0 ]
【答案】A
【解析】
【分析】根据分段函数的最值,结合二次函数和基本不等式,二次不等式求解.
( x+a )2 ,x≤0
【详解】由于 f
(
x
)=
1
,则当x=0, f
(
0
)=a2
.由于 f
(
0
)
是 f
(
x
)
的最小值,
x+ +a,x>0
x
第3页/共21页
学科网(北京)股份有限公司1
则(−∞,0]为减区间,即有a≤0.则a2 ≤ x+ +a,x >0恒成立.
x
1 1
由x+ ≥2 x× =2,当且仅当x=1取最值.则 a2 ≤2+a,解得−1≤a ≤2。
x x
则a的取值范围为
[−1,0 ]
.
故选:A.
x2 y2
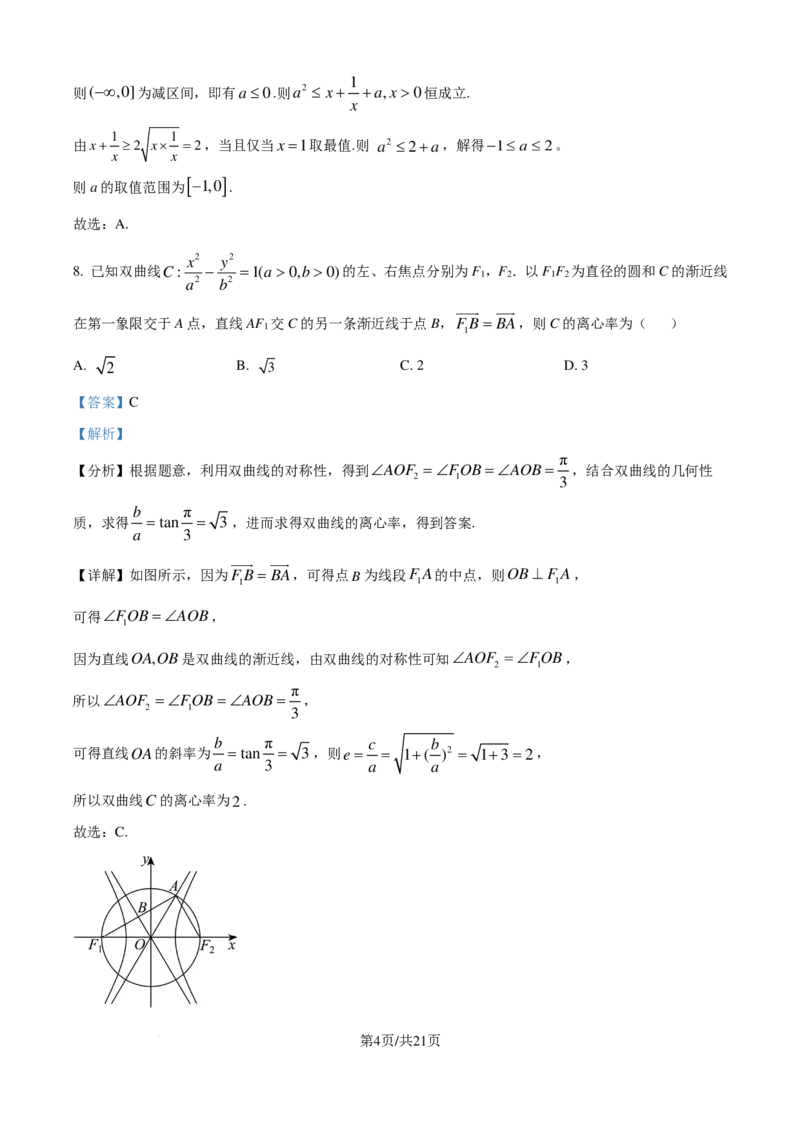
8. 已知双曲线C: − =1(a >0,b>0)的左、右焦点分别为F ,F .以F F 为直径的圆和C的渐近线
1 2 1 2
a2 b2
在第一象限交于A点,直线AF 交C的另一条渐近线于点B,FB= BA,则C的离心率为( )
1 1
A. 2 B. 3 C. 2 D. 3
【答案】C
【解析】
π
【分析】根据题意,利用双曲线的对称性,得到∠AOF =∠FOB=∠AOB= ,结合双曲线的几何性
2 1 3
b π
质,求得 =tan = 3,进而求得双曲线的离心率,得到答案.
a 3
【详解】如图所示,因为FB= BA,可得点B为线段FA的中点,则OB⊥ FA,
1 1 1
可得∠FOB=∠AOB,
1
因为直线OA,OB是双曲线的渐近线,由双曲线的对称性可知∠AOF =∠FOB,
2 1
π
所以∠AOF =∠FOB=∠AOB= ,
2 1 3
b π c b
可得直线OA的斜率为 =tan = 3,则e= = 1+( )2 = 1+3 =2,
a 3 a a
所以双曲线C的离心率为2.
故选:C.
第4页/共21页
学科网(北京)股份有限公司二、选择题:本题共 3小题,每小题 6分,共 18分.在每小题给出的四个选项中,有多项符
合题目要求.全部选对的得 6分,部分选对的得部分分,有选错的得 0分.
9. 一组数据:x ,x ,…,x 是公差为-2的等差数列,去掉首末两项x ,x 后得到一组新数据,则( )
1 2 10 1 10
A. 两组数据的极差相同 B. 两组数据的中位数相同
C. 两组数据的平均数相同 D. 两组数据的标准差相同
【答案】BC
【解析】
【分析】根据平均数的概念结合等差数列的性质判断C,由中位数的概念可判断B,由方差及等差数列的
通项公式计算即可判断D,根据极差及等差数列的通项公式可判断A.
1 1 1
【详解】对于C,原数据的平均数为x = (x +x ++x )= ×5(x + x )= (x +x ),
10 1 2 10 10 5 6 2 5 6
1 1 1
去掉x,x 后的平均数为x′= (x +x ++x )= ×4(x +x )= (x +x )= x ,则C正确;
1 10 8 2 3 9 8 5 6 2 5 6
1
对于B,原数据的中位数为 (x +x ),
2 5 6
1
去掉x,x 后的中位数仍为 (x +x ),即中位数没变,则B正确;
1 10 2 5 6
对于A,原数据的极差为x −x =−9d =18,
1 10
去掉x,x 后的极差为x −x =−7d =14,即极差变小,则A错误;
1 10 2 9
对于D,设公差为d,则原数据的方差为
2 2 2
1 1 1 1
s2 = 10 x 1 − 2 (x 5 +x 6 ) + x 2 − 2 (x 5 +x 6 ) ++ x 10 − 2 (x 5 +x 6 )
1 9 7 5 3 1 1
= [(− d)2 +(− d)2 +(− d)2 +(− d)2 +(− d)2 +( d)2 +
10 2 2 2 2 2 2
3 5 7 9
( d)2 +( d)2 +( d)2 +( d)2]=33,
2 2 2 2
2 2 2
1 1 1 1
去掉x 1 ,x 10 后的方差为s′2 = 8 x 2 − 2 (x 5 +x 6 ) + x 3 − 2 (x 5 +x 6 ) ++ x 9 − 2 (x 5 +x 6 )
1 7 5 3 1 1 3 5 7
= [(− d)2 +(− d)2 +(− d)2 +(− d)2 +( d)2 +( d)2 +( d)2 +( d)2]=21,
8 2 2 2 2 2 2 2 2
即方差变小.标准差也变小,则D错误.
故选:BC
10. 平面α过正方体ABCD− ABC D 的顶点A,平面α//平面CBD ,平面α平面ABCD=m,平
1 1 1 1 1 1
第5页/共21页
学科网(北京)股份有限公司面α平面ABB A =n,则( )
1 1
π
A. BD //m B. AB//平面α C. n⊥平面ADC B D. m,n所成的角为
1 1 1 1 1
3
【答案】ABC
【解析】
【分析】设平面α平面ABC D =m′ 证得m//m′和m′//BD ,可判定A正确;过DC作平面 γ ,
1 1 1 1 1 1 1
设平面γ平面α=a,证得AB//a,可判定B正确;设平面α平面DCC D =n′,证得n′⊥平面
1 1 1
ADC B ,可判定C正确;把m,n所成的角转化为BD与DC所成的角,结合CB D 为等边三角形,可
1 1 1 1 1 1 1
判定D不正确.
【详解】对于A中,设平面α平面ABC D =m′
1 1 1 1
在正方体ABCD− ABC D 中,可得平面ABCD//平面ABC D ,
1 1 1 1 1 1 1 1
因为平面α平面ABCD=m,所以m//m′,
又因为平面α//平面CBD ,且平面α平面ABC D =m′,
1 1 1 1 1 1
平面CBD ∩平面ABC D = BD ,所以m′//BD ,所以m//BD ,所以A正确;
1 1 1 1 1 1 1 1 1 1 1 1
对于B中,在正方体ABCD− ABC D 中,可得AB//DC,
1 1 1 1 1 1
因为平面α//平面CBD ,且平面DC ⊂平面CBD ,所以DC//平面α,
1 1 1 1 1 1
过DC作平面 γ ,设平面γ平面α=a,可得DC//a,
1 1
可得AB//a,且AB⊄α,所以AB//平面α,所以B正确;
1 1 1
对于C中,设平面α平面DCC D =n′,
1 1
因为平面α//平面CBD 且平面CBD ∩平面DCC D = DC ,所以n′//DC ,
1 1 1 1 1 1 1 1
在正方体ABCD− ABC D 中,可得AD ⊥平面DCC D ,
1 1 1 1 1 1
因为DC ⊂平面DCC D ,所以AD⊥ DC,
1 1 1 1
又因为DC ⊥DC,且ADDC = D,AD,DC ⊂平面ADC B ,
1 1 1 1 1 1
所以DC ⊥平面ADC B ,所以n′⊥平面ADC B ,
1 1 1 1 1
在正方体ABCD− ABC D 中,可得平面ABB A //平面DCC D ,
1 1 1 1 1 1 1 1
第6页/共21页
学科网(北京)股份有限公司因为平面α平面DCC D =n′,平面α平面ABB A =n,所以n//n′,
1 1 1 1
所以n⊥平面ADC B ,所以C正确;
1 1
对于D中,因为m//BD 且n//DC,所以m,n所成的角,即为BD与DC所成的角,
1 1 1 1 1 1
π
因为CB D 为等边三角形,可得∠CDB = ,
1 1 1 1 3
π
所以异面直线m,n所成的角为 ,所以D不正确.
3
故选:ABC.
m 1+a
11. 设数列 和 的项数均为m,称∑ a −b 为数列 和 的距离.记满足a = n 的所有数
i i n+1 1−a
i=1 n
{𝑎𝑎𝑛𝑛} {𝑏𝑏𝑛𝑛} {𝑎𝑎𝑛𝑛} {𝑏𝑏𝑛𝑛}
列 构成的集合为C.已知数列 { A } 和 { B } 为C中的两个元素,项数均为m,下列正确的有( )
n n
{𝑎𝑎𝑛𝑛}
A. 数列1,3,5,7和数列2,4,6,8的距离为4
( )
B. 若m=4p p∈N* ,则AA A = BB B
1 2 m 1 2 m
m
C. 若m=4p ( p∈N* ) ,则∑ A ≤m
i
i=1
D. 若A =2,B =3,数列 { A } 和 { B } 的距离小于2017,则m的最大值为3456
1 1 n n
【答案】ABD
【解析】
【分析】根据数列距离的定义求两数列的距离判断A,结合数列 { A } , { B } 的递推关系证明两数列具有
n n
m
周期性,判断B,利用基本不等式求 A + A + A + A ,由此求∑ A ,判断C,由条件求
4k+1 4k+2 4k+3 4k+4 i
i=1
4 7 3456 3457
∑ A −B = ,结合周期性可求∑ A −B ,∑ A −B ,由此判断D.
i i 3 i i i i
i=1 i=1 i=1
【详解】对于A,根据数列距离的定义可得:
第7页/共21页
学科网(北京)股份有限公司数列1,3,5,7和数列2,4,6,8的距离为1−2 + 3−4 + 5−6 + 7−8 =4,A正确;
1+ A
对于B,设A =t,其中t ≠0,且t ≠±1,由A = n ,
1 n+1 1−A
n
1+t 1 t−1
所以A = ,A =− ,A = ,A =t,
2 1−t 3 t 4 t+1 5
则A = A ,
1 5
{ }
因此数列 A 中的项周期性重复,且间隔4项重复一次,
n
所以A A A A =1,1≤k ≤ p−1, p∈N∗,
4k+1 4k+2 4k+3 4k+4
1+B
设B = s,其中s ≠0,且s ≠±1,由B = n ,
1 n+1 1−B
n
1+s 1 s−1
所以B = ,B =− ,B = ,B =s,
2 1−s 3 s 4 s+1 5
则B = B ,
1 5
{ }
因此数列 B 中的项周期性重复,且间隔4项重复一次,
n
所以B B B B =1,1≤k ≤ p−1, p∈N∗,
4k+1 4k+2 4k+3 4k+4
( )
所以若m=4p p∈N* ,则AA A = BB B ,B正确;
1 2 m 1 2 m
1+t 1 t−1
因为 A + A + A + A = t + + − + ,其中t ≠0,且t ≠±1,
4k+1 4k+2 4k+3 4k+4 1−t t t+1
1 t+1 t−1
所以 t ≠ , ≠ ,
t t−1 t+1
1 t+1 t−1
所以 A + A + A + A = t + + + >2+2=4,
4k+1 4k+2 4k+3 4k+4 t t−1 t+1
m
所以若m=4p ( p∈N* ) ,∑ A >4p=m,C错误;
i
i=1
1 1
所以数列 { A } 中,A =2,A =−3,A =− ,A = ,k∈N∗,
n 4k−3 4k−2 4k−1 2 4k 3
1 1
故 { B } 中,B =3,B =−2,B =− ,B = ,k∈N∗,
n 4k−3 4k−2 4k−1 3 4k 2
k+1 k
∑ b −c ≥∑ b −c ,
i i i i
i=1 i=1
第8页/共21页
学科网(北京)股份有限公司所以项数m越大,数列 { A } 和 { B } 的距离越大,
n n
4 7 3456 7
由∑ A −B = ,可得∑ b −c = ×864=2016,
i i 3 i i 3
i=1 i=1
3457
∑ b −c =2016+1=2017,
i i
i=1
m
所以m≤3456时,∑ b −c <2017,
i i
i=1
故m的最大值为3456;
所以数列 { A } 和 { B } 的距离小于2017,则m的最大值为3456,D正确.
n n
故选:ABD.
【点睛】“新定义”主要是指即时定义新概念、新公式、新定理、新法则、新运算五种,然后根据此新定
义去解决问题,有时还需要用类比的方法去理解新的定义,这样有助于对新定义的透彻理解.但是,透过现
象看本质,它们考查的还是基础数学知识,所以说“新题”不一定是“难题”,掌握好三基,以不变应万
变才是制胜法宝.
三、填空题:本题共 3个小题,每小题 5分,共 15分.
12. 若曲线y =axcosx在点 ( 0,0 ) 处的切线斜率为−1,则a= ______.
【答案】−1
【解析】
【分析】先求导,再代入0,运用导数几何意义可解.
【详解】求导得到y′=a(cosx−xsinx),将0代入导数,运用导数几何意义,得
a(cos0−sin0)=a = −1.
故答案为:−1.
π
13. 若x = ,x =π是函数 f ( x )=sinωx (ω>0 ) 的两个相邻极值点,则ω= ______.
1 3 2
3
【答案】
2
【解析】
【分析】根据题意得到借助最小正周期公式,再用两个相邻极值点相差半个周期可解.
π 1 π
【详解】x = ,x =π是函数 f ( x )=sinωx (ω>0 ) 的两个相邻极值点,则 T =(π− ),
1 3 2 2 3
第9页/共21页
学科网(北京)股份有限公司1 2π π 3
即 × =(π− ),解得ω= .
2 ω 3 2
3
故答案为:
2
14. 正方体ABCD-ABC D 的棱长为3,P是侧面ADD A(包括边界)上一动点,E是棱CD上一点,
1 1 1 1 1 1
若∠APB=∠DPE,且△APB的面积是DPE面积的9倍,则三棱锥P-ABE体积的最大值是______.
9 2
【答案】
8
【解析】
【分析】由条件先证明APB∽EPD,结合面积关系可得AP=3PD,在平面ADD A上建立平面直角坐
1 1
标系,确定点P的轨迹方程,结合体积公式求三棱锥P-ABE体积的最大值.
【详解】由已知AB⊥平面ADD A,AP⊂平面ADD A,
1 1 1 1
所以AB⊥ AP,
因为DE ⊥平面ADD A,DP⊂平面ADD A,
1 1 1 1
所以DE ⊥ DP,
所以∠BAP=∠EDP=90,又∠APB=∠DPE,
所以APB∽DPE,又△APB的面积是DPE面积的9倍,
AP 1
所以 = ,
DP 3
以点D为原点,DA,DC,DD 为x,y,z轴建立空间直角坐标系,
1
( ) ( )
则A 3,0,0 ,D 0,0,0 ,
( )
设点P的坐标为 x,0,z ,则0≤ x≤3,0≤ z ≤3,
由已知 AP =3 PD ,
所以 ( x−3 )2 +z2 =3 x2 +z2 ,
3 9
所以x2 +z2 + x− =0,其中0≤ x≤3,0≤ z ≤3,
4 8
3 9
所以点P的轨迹为以点 − ,0,0为圆心, 为半径的圆在侧面ADD A内的一段圆弧,
8 8 1 1
第10页/共21页
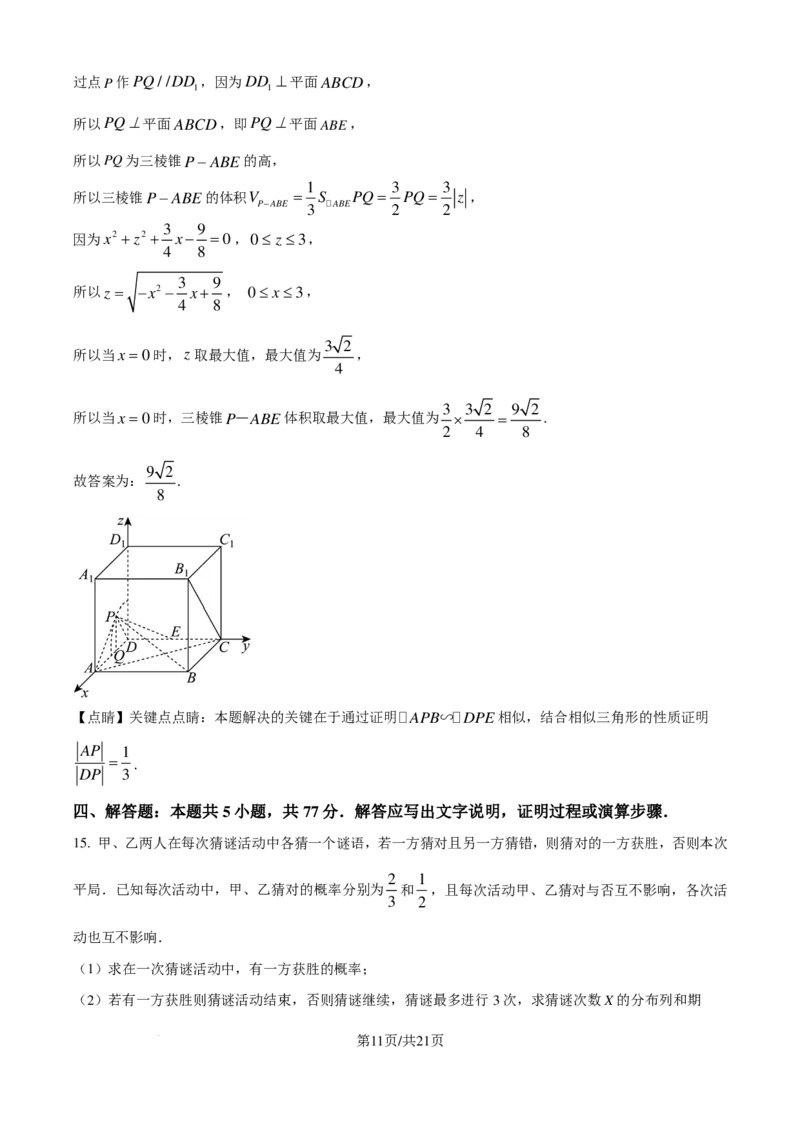
学科网(北京)股份有限公司过点P作PQ//DD ,因为DD ⊥平面ABCD,
1 1
所以PQ⊥平面ABCD,即PQ⊥平面ABE,
所以PQ为三棱锥P−ABE的高,
1 3 3
所以三棱锥P−ABE的体积V = S PQ= PQ= z ,
P−ABE
3
ABE
2 2
3 9
因为x2 +z2 + x− =0,0≤ z ≤3,
4 8
3 9
所以z = −x2 − x+ , 0≤ x≤3,
4 8
3 2
所以当x=0时,z取最大值,最大值为 ,
4
3 3 2 9 2
所以当x=0时,三棱锥P-ABE体积取最大值,最大值为 × = .
2 4 8
9 2
故答案为: .
8
【点睛】关键点点睛:本题解决的关键在于通过证明APB∽DPE相似,结合相似三角形的性质证明
AP 1
= .
DP 3
四、解答题:本题共 5小题,共 77分.解答应写出文字说明,证明过程或演算步骤.
15. 甲、乙两人在每次猜谜活动中各猜一个谜语,若一方猜对且另一方猜错,则猜对的一方获胜,否则本次
2 1
平局.已知每次活动中,甲、乙猜对的概率分别为 和 ,且每次活动甲、乙猜对与否互不影响,各次活
3 2
动也互不影响.
(1)求在一次猜谜活动中,有一方获胜的概率;
(2)若有一方获胜则猜谜活动结束,否则猜谜继续,猜谜最多进行3次,求猜谜次数X的分布列和期
第11页/共21页
学科网(北京)股份有限公司望.
1
【答案】(1)
2
7
(2)分布列见解析,
4
【解析】
【分析】(1)有一方获胜,意味着结果为一对一错,分情况用相互独立事件的乘法公式计算相加即可;
(2)确定X 取每一个值对应时间的概率,即可求解.
【小问1详解】
设甲猜对为事件A,乙猜对为事件B,
事件AB+ AB表示“星队”第一轮活动中只有1人猜对,且事件AB与AB互斥,
则P ( AB ) = P ( A ) ×P ( B )= 1 ,P ( AB ) = P ( A )×P ( B ) = 1 ,
6 3
( ) ( ) ( ) 1 1
∴P AB+ AB = P AB +P AB = ,即有一方获胜的概率为 .
2 2
【小问2详解】
由题意X 的可能取值为1,2,3
1
X =1表示第一次猜谜有人获胜,所以 p ( X =1 )= ,
2
1 1 1
X =2表示第一次猜谜没人获胜同时第二次猜谜有人获胜,所以 p ( X =2 )= × =
2 2 4
1 1 1
由分布列的性质,可得 p ( X =3 )=1− − = ,
2 4 4
所以分布列为
X 1 2 3
1 1 1
p
2 4 4
1 1 1 7
所以E ( X )=1× +2× +3× =
2 4 4 4
a
16. 已知ABC的内角A,B,C 的对边分别为a,b,c, 2 ( ccosB+bcosC )= .
cosA
(1)求A;
1
(2)若AB边上的高等于 c,求sinC.
3
第12页/共21页
学科网(北京)股份有限公司π
【答案】(1)
4
3 10
(2)
10
【解析】
【分析】(1)利用正弦定理,边化角,结合两角和的正弦公式化简即可;
(2)先用c表示ABC中线段的长度,然后利用等面积法求解即可.
【小问1详解】
a sinA
由 2 ( ccosB+bcosC )= 得 2 ( sinCcosB+sinBcosC )= ,
cosA cosA
所以 2sin ( B+C )= sinA ,即 2sinA= sinA ,又sinA≠0,所以cosA= 2 ,
cosA cosA 2
π
又0< A<π,得A= .
4
【小问2详解】
由题得示意图
1
作CD⊥ AB,则 CD = c,
3
π 1 2 2
因为A= ,所以 AD = CD = c,得 AC = c, DB = c,
4 3 3 3
5 1 1
所以 BC = c,利用等面积法可知: AB CD = AC BC sinC
3 2 2
1 2 5
即c× c= c× c×sinC,
3 3 3
3 10
解得:sinC = .
10
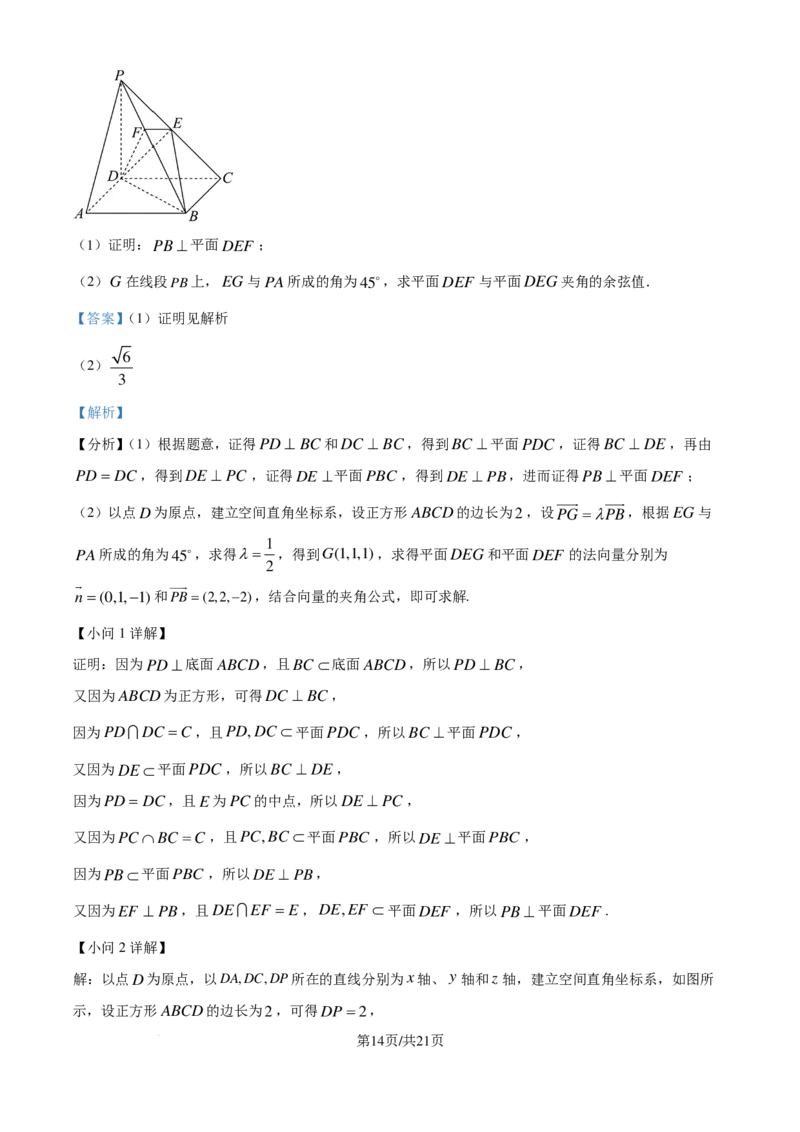
17. 如图,在四棱锥P−ABCD中,底面四边形ABCD是正方形,PD= DC,PD⊥底面ABCD,E是
线段PC的中点,F 在线段PB上,EF ⊥ PB.
第13页/共21页
学科网(北京)股份有限公司(1)证明:PB⊥平面DEF ;
(2)G在线段PB上,EG与PA所成的角为45,求平面DEF 与平面DEG夹角的余弦值.
【答案】(1)证明见解析
6
(2)
3
【解析】
【分析】(1)根据题意,证得PD⊥ BC和DC ⊥ BC,得到BC ⊥平面PDC,证得BC ⊥ DE,再由
PD= DC,得到DE ⊥ PC ,证得DE ⊥平面PBC ,得到DE ⊥ PB,进而证得PB⊥平面DEF ;
(2)以点D为原点,建立空间直角坐标系,设正方形ABCD的边长为2,设PG =λPB,根据EG与
1
PA所成的角为45,求得λ= ,得到G(1,1,1),求得平面DEG和平面DEF 的法向量分别为
2
n=(0,1,−1)和PB=(2,2,−2),结合向量的夹角公式,即可求解.
【小问1详解】
证明:因为PD⊥底面ABCD,且BC ⊂底面ABCD,所以PD⊥ BC,
又因为ABCD为正方形,可得DC ⊥ BC,
因为PDDC =C,且PD,DC ⊂平面PDC,所以BC ⊥平面PDC,
又因为DE ⊂平面PDC,所以BC ⊥ DE,
因为PD= DC,且E为PC的中点,所以DE ⊥ PC ,
又因为PC∩BC =C,且PC,BC ⊂平面PBC ,所以DE ⊥平面PBC ,
因为PB⊂平面PBC ,所以DE ⊥ PB,
又因为EF ⊥ PB,且DEEF = E,DE,EF ⊂平面DEF ,所以PB⊥平面DEF .
【小问2详解】
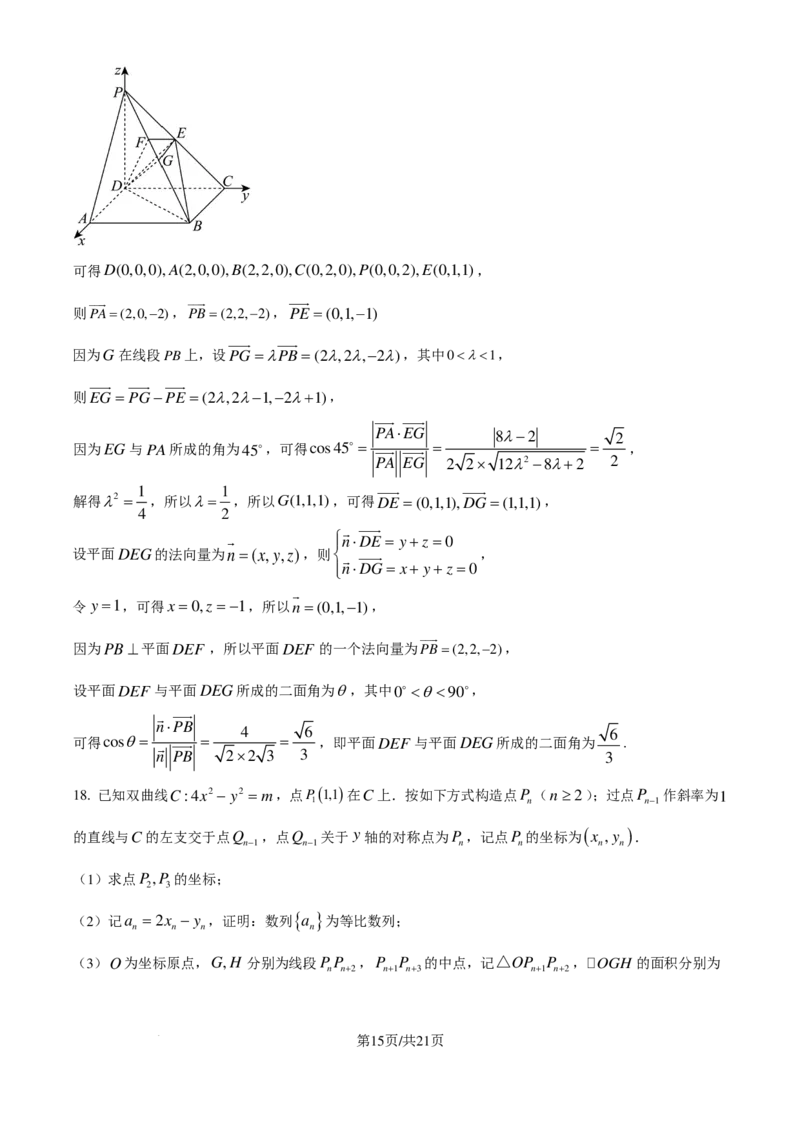
解:以点D为原点,以DA,DC,DP所在的直线分别为x轴、 y轴和z轴,建立空间直角坐标系,如图所
示,设正方形ABCD的边长为2,可得DP=2,
第14页/共21页
学科网(北京)股份有限公司可得D(0,0,0),A(2,0,0),B(2,2,0),C(0,2,0),P(0,0,2),E(0,1,1),
则PA=(2,0,−2),PB=(2,2,−2),PE =(0,1,−1)
因为G在线段PB上,设PG =λPB=(2λ,2λ,−2λ),其中0<λ<1,
则EG = PG−PE =(2λ,2λ−1,−2λ+1),
PA⋅EG 8λ−2 2
因为EG与PA所成的角为45,可得cos45 = = = ,
PA EG 2 2× 12λ2 −8λ+2 2
1 1
解得λ2 = ,所以λ= ,所以G(1,1,1),可得DE =(0,1,1),DG =(1,1,1),
4 2
n⋅DE = y+z =0
设平面DEG的法向量为n=(x,y,z),则 ,
n⋅DG = x+ y+z =0
令 y =1,可得x =0,z = −1,所以n=(0,1,−1),
因为PB⊥平面DEF ,所以平面DEF 的一个法向量为PB=(2,2,−2),
设平面DEF 与平面DEG所成的二面角为θ,其中0 <θ<90,
n⋅PB
4 6 6
可得cosθ= = = ,即平面DEF 与平面DEG所成的二面角为 .
n PB 2×2 3 3 3
18. 已知双曲线C:4x2 − y2 =m,点P(1,1)在C上.按如下方式构造点P(n≥2);过点P 作斜率为1
1 n n−1
的直线与C的左支交于点Q ,点Q 关于 y轴的对称点为P ,记点P 的坐标为 ( x ,y ) .
n−1 n−1 n n n n
(1)求点P,P 的坐标;
2 3
(2)记a =2x − y ,证明:数列 { a } 为等比数列;
n n n n
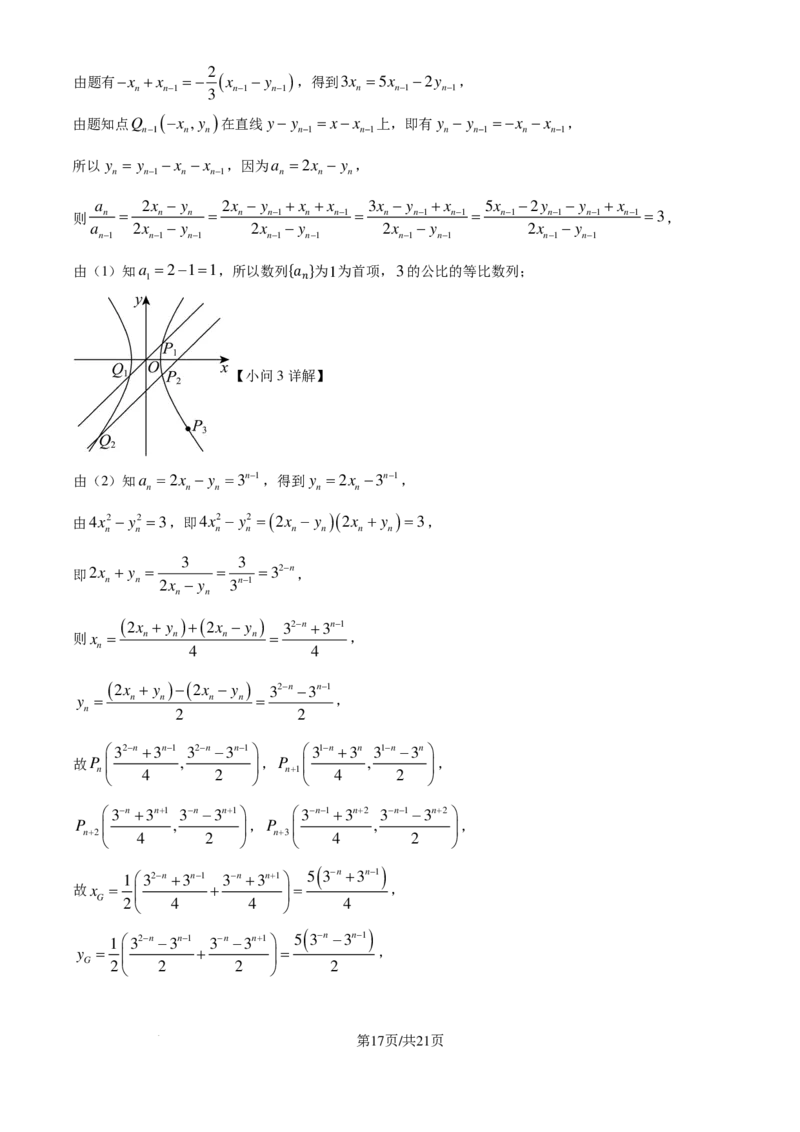
(3)O为坐标原点,G,H 分别为线段PP ,P P 的中点,记△OP P ,OGH 的面积分别为
n n+2 n+1 n+3 n+1 n+2
第15页/共21页
学科网(北京)股份有限公司S
S ,S ,求 1 的值.
1 2 S
2
7 13
【答案】(1)P(1,−1),P
,−
2 3 3 3
S 9
(2)证明见解析 (3) 1 =
S 25
2
【解析】
【分析】(1)由点P ( 1,1 ) 可得m的值,求出l 的方程后联立双曲线可得Q ,即可得P ,再借助l 的方
1 P 1 Q 1 1 2 P 2 Q 2
程后联立双曲线可得Q ,即可得P ;
2 3
(2)联立y− y = x−x 与双曲线方程,结合韦达定理可得3x =5x −2y ,结合点Q (−x ,y )
n−1 n−1 n n−1 n−1 n−1 n n
代入可得y = y −x −x ,再利用等比数列定义与判定定理计算即可得证;
n n−1 n n−1
(3)由2x − y =3n−1,结合4x2 − y2 =3,从而可得x 与 y ,再利用面积公式分别计算出S ,S 即可得.
n n n n n n 1 2
【小问1详解】
由题知m =4−1=3,所以双曲线C:4x2 − y2 =3,
又过点P ( 1,1 ) ,斜率为1的直线方程为y = x,
1
由双曲线与直线的对称性可知Q (−1,−1),所以P(1,−1),
1 2
又过P(1,−1),且斜率为1的直线方程为y+1= x−1,即y = x−2,
2
y = x−2 7 7 7 13
由 ,解得x=1或x =− ,当x =− 时,y =− −2=− ,
4x2 − y2 =3 3 3 3 3
7 13 7 13
所以Q − ,− ,所以P ,− ;
2 3 3 3 3 3
【小问2详解】
设P (x ,y )(n≥2,n∈N∗),
n−1 n−1 n−1
则过P (x ,y )(n≥2,n∈N∗),且斜率为1的直线方程为y− y = x−x ,
n−1 n−1 n−1 n−1 n−1
y− y = x−x
联立 n−1 n−1,消 y得到3x2 +2 ( x − y ) x−( x − y )2 −3=0,
4x2 − y2 =3 n−1 n−1 n−1 n−1
第16页/共21页
学科网(北京)股份有限公司2
由题有−x +x =− ( x − y ),得到3x =5x −2y ,
n n−1 3 n−1 n−1 n n−1 n−1
由题知点Q (−x ,y ) 在直线y− y = x−x 上,即有y − y =−x −x ,
n−1 n n n−1 n−1 n n−1 n n−1
所以y = y −x −x ,因为a =2x − y ,
n n−1 n n−1 n n n
a 2x − y 2x − y +x +x 3x − y +x 5x −2y − y +x
则 n = n n = n n−1 n n−1 = n n−1 n−1 = n−1 n−1 n−1 n−1 =3,
a 2x − y 2x − y 2x − y 2x − y
n−1 n−1 n−1 n−1 n−1 n−1 n−1 n−1 n−1
由(1)知a =2−1=1,所以数列 为1为首项,3的公比的等比数列;
1
{𝑎𝑎𝑛𝑛}
【小问3详解】
由(2)知a =2x − y =3n−1,得到y =2x −3n−1,
n n n n n
由4x2 − y2 =3,即4x2 − y2 =( 2x − y )( 2x + y )=3,
n n n n n n n n
3 3
即2x + y = = =32−n,
n n 2x − y 3n−1
n n
( 2x + y )+( 2x − y ) 32−n +3n−1
则x = n n n n = ,
n 4 4
( 2x + y )−( 2x − y ) 32−n −3n−1
y = n n n n = ,
n 2 2
32−n +3n−1 32−n −3n−1 31−n +3n 31−n −3n
故P , ,P , ,
n 4 2 n+1 4 2
3−n +3n+1 3−n −3n+1 3−n−1+3n+2 3−n−1−3n+2
P , ,P , ,
n+2
4 2
n+3
4 2
132−n +3n−1 3−n +3n+1 5 ( 3−n +3n−1 )
故x = + = ,
G 2 4 4 4
132−n −3n−1 3−n −3n+1 5 ( 3−n −3n−1 )
y = + = ,
G 2 2 2 2
第17页/共21页
学科网(北京)股份有限公司5 ( 3−n +3n−1 ) 5 ( 3−n −3n−1 ) 5 ( 3−n−1+3n ) 5 ( 3−n−1−3n )
即G , ,则H , ,
4 2 4 2
1 1 31−n +3n 3−n −3n+1 3−n +3n+131−n −3n
则S = x y −x y = −
1 2 n+1 n+2 n+2 n+1 2 4 2 4 2
1
( 31−n +3n )( 3−n −3n+1 ) − ( 3−n +3n+1 )( 31−n −3n )
=
2 8
1 31−2n +1−9−32n+1−31−2n −9+1+32n+1
=
2 8
1 −16
= =1,
2 8
1 1 5 ( 3−n +3n−1 ) 5 ( 3−n−1−3n ) 5 ( 3−n−1+3n ) 5 ( 3−n −3n−1 )
S = x y −x y = −
2 2 G H H G 2 4 2 4 2
= 1 × 25 ( 3−n +3n−1 )( 3−n−1−3n ) − ( 3−n−1+3n )( 3−n −3n−1 )
2 8
25 1 1
= 3−2n−1−1+ −32n−1−3−2n−1−1+ +32n−1
16 9 9
25 −16 25
= = ,
16 9 9
S 1 9
1 = =
故S 25 25.
2
9
【点睛】关键点点睛:本题最后一问关键点在于得到2x − y =3n−1后,结合4x2 − y2 =3,从而可得x
n n n n n
与 y ,再利用面积公式计算即可得.
n
19. 已知函数 f ( x ) 定义域为I ,D⊆ I ,若∀x∈D,∃t∈D,当x0 𝑥𝑥 ∈(0,+∞) 𝑓𝑓 (𝑥𝑥)<0
即 f
(
x
)
在
(−1,0 )
上单调递增,在 上单调递减,
(0,+∞)
即对∀x∈(−1,0 ] ,∃t∈(−1,0 ] ,当x0时,令ax+2a−2=0,则x= = −2,
a a
2
则当
−2≤0,即a≥1时,g′(
x
)≥0,即g (
x
)
在 上单调递增,
a
[0,1]
则
f′(
x
)=
g
(
x
)≥
g
(
0
)=0,即
f
(
x
)
在 上单调递增,
[0,1]
有 f
(
x
)≥
f
(
0
)
,不符合要求,故舍去;
2 2
当 −2≥1,即00,
a a
2 2
即g ( x ) 在0, −2上单调递减,在 −2,1上单调递增,
a a
2
则若需 f ( x )≤ f ( 0 ) 恒成立,有 ,解得a≤ −2,
ln2
e2
ln 2
由 2 2−3ln2 lne2 −ln23 8 ,故 −2<1,
−2−1= = = <0 ln2
ln2 ln2 ln2 ln2
2 2
由 ,故 −2> ,
3
3 4 e ln2 3
2 2 2(3−4ln2) 2(lne −ln2 ) ln16
2 2
即l当n2−<2
a
−≤3= 3−ln
2
2时, = 符合3l要n2求; = ln2 >0
3 ln2
2
综上所述,a≤ −2;
ln2
【小问2详解】
若 f
(
x
)
在D上的“Ω点”个数为0,则 f
(
m
)≤
f
(
1
)=0,符合要求;
若 f ( x ) 在D上的“Ω点”个数为s∈N*,令 f ( x ) 在D上的“Ω点”分别为i 、i 、、i ,
1 2 s
其中i 1,由题意 f ( i −1 )< f ( i ) , f ( 1 )< f ( i ) , f ( i −1 )≤ f ( 1 ) ,
k 1 1 1 1
第20页/共21页
学科网(北京)股份有限公司故0< f ( i )− f ( 1 )≤1,即0< f ( i )≤1,又 f ( m )≤ f ( i ) ,故 f ( m )≤1,符合要求;
1 1 1
若s≥2,
则 , ,, ,
由𝑓𝑓f (𝑖𝑖(1 x ))−−𝑓𝑓f (1() x=−1𝑓𝑓)(≤𝑖𝑖1) 1>,0则0𝑓𝑓<(𝑖𝑖2 f )(−i 𝑓𝑓)(−𝑖𝑖1 f )(>i 0−1 )≤1,𝑓𝑓( 𝑖𝑖𝑠𝑠)−𝑓𝑓(𝑖𝑖𝑠𝑠−1)>0
k k
若i −i =1,即i =i −1,则0< f ( i )− f ( i )≤1,
k k−1 k−1 k k k−1
若i −i = j >1,由题意 f ( i + j−1 )= f ( i −1 )< f ( i ) , f ( i )< f ( i ) ,且
k k−1 k−1 k k k−1 k
f ( i −1 )≤ f ( i ) ,
k k−1
又0< f ( i )− f ( i −1 )≤1,故0< f ( i )− f ( i )≤1,即0< f ( i )− f ( i )≤1,
k k k k−1 2 1
0< f ( i )− f ( i )≤1,,0< f ( i )− f ( i )≤1,
3 2 s s−1
即有0< f ( i )− f ( i )+ f ( i )− f ( i )+− f ( i )≤s−1,即0< f ( i )− f ( i )≤s−1,
2 1 3 2 s−1 s 1
由0< f ( i )≤1,故0< f ( i )≤s,
1 s
又 f
(
m
)≤
f
(
i
)
,故 f
(
m
)≤s,
s
( ) ( )
即 f x 在D上的“Ω点”个数不小于 f m .
【点睛】关键点点睛:最后一问关键点在于借助 f ( x )− f ( x−1 )≤1,结合定义得到相邻两个“Ω点”的函
( )
数值之差小于等于1,即可得“Ω点”个数与 f m 的关系.
第21页/共21页
学科网(北京)股份有限公司