文档内容
宜春一中 2024—2025 学年第二学期高二年级期中考试 的解集为( )
A. B. C. D.
数学试卷
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题
符合题目要求的.
目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9. 已知实数数列 的前n项和为 ,下列说法正确的是( )
1. 已知函数 在 处可导,且 ,则 ( )
A.若数列 为等差数列,则 是等差数列
A. B. C. D. 2
B.若数列 为等差数列,则 , , ,…为等差数列
2.若数列 各项均为正数,则“ 为等比数列”是“ 为等差数列”的( )
C.若数列 为等比数列,且 , ,则
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
D.若数列 为等比数列,则 , , ,…为等比数列
3.已知数列 满足 ,若 ,则 ( )
A.28 B.13 C.18 D.20 10. 已知函数 ,则下列结论正确的是( )
4.在公差不为0的等差数列 中,若 是 与 的等差中项,则 的最小值为( ) A.函数 存在两个不同的零点
B.函数 既存在极大值又存在极小值
A. B. C. D.
C.当 时,方程 有且只有两个实根
5.在等比数列 中, , 是函数 的极值点,则 ( )
D.若 时, ,则t的最小值为2
A.3 B. C.-4 D.4
6.已知函数f(x)是奇函数,函数g(x)是偶函数,且当x>0时,f '(x)>0,g'(x)>0,则当x<0时, 11. 已知数列 的前 项和为 ,且满足 , , ,
以下说法正确的是( ) 则下列说法正确的有( )
f '(x)
A.f '(x)+g'(x)>0 B.f '(x)—g'(x)>0 C.f '(x)g'(x)>0 D. >0 A. 数列 为等比数列 B. 数列 为等差数列
g'(x)
C. D.
7.已知函数 的图象在点 处的切线的斜率为 ,则数列 的前
项和 为( )
三、填空题:本题共3小题,每小题5分,共15分.
A. B. C. D.
12.记 为等差数列 的前 项和,若 ,则 .
13.若不等式 有解,则实数m的取值范围为 .
8.已知函数 在 上可导,且f (1)=1,其导函数 满足 ,则不等式 14.已知数列 满足 , ,则 .四、解答题(本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.)
18.已知函数 .
15.在数列 中, , .
(1)求函数f(x)的单调区间.
(1)求数列 的通项公式;
(2)当 时,若对任意 ,不等式 恒成立, 求 的最小值.
(2)若 ,求数列 的前n项和 .
16.已知函数 .
19.对于数列 ,如果存在一个正整数 ,使得对任意 ,都有 成立,那么就把这
(1)求函数 在点 处的切线方程;
样的一类数列 称作周期为 的周期数列, 的最小值称作数列 的最小正周期,简称周期.
(2)求 的单调区间和极值.
(1)判断数列 是否为周期数列,如果是,写出该数列的周期,如果不是,说明理由.
(2)已知无穷数列 是周期为2的周期数列,且 , , 是数列 的前 项和,若
对一切正整数 恒成立,求常数 的取值范围;
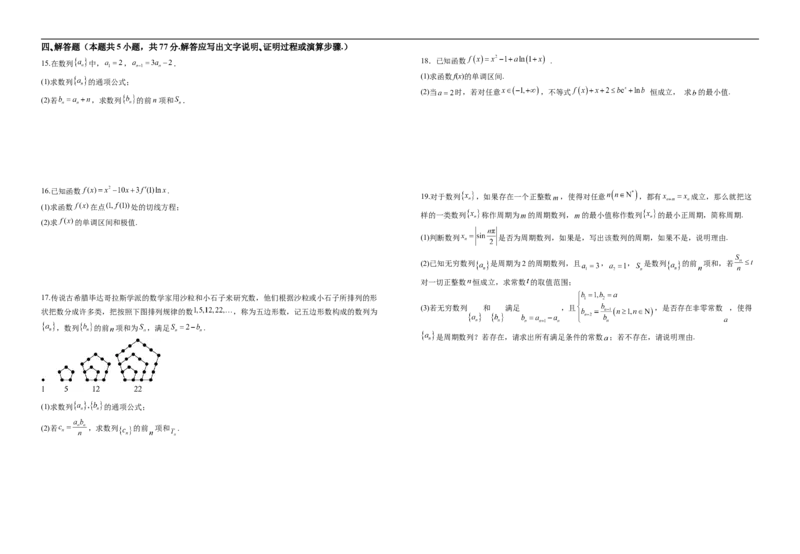
17.传说古希腊毕达哥拉斯学派的数学家用沙粒和小石子来研究数,他们根据沙粒或小石子所排列的形
(3)若无穷数列 和 满足 ,且 ,是否存在非零常数 ,使得
状把数分成许多类,把按照下图排列规律的数 ,称为五边形数,记五边形数构成的数列为
,数列 的前 项和为 ,满足 .
是周期数列?若存在,请求出所有满足条件的常数 ;若不存在,请说明理由.
(1)求数列 的通项公式;
(2)若 ,求数列 的前 项和 .则 ,解得 ,于是 , ,
所以所求切线方程为: ,即 ............................6'
宜春一中 2024—2025 学年第二学期高二年级期中考试
(2)由(1)知,函数 ,定义域为 ,求导得
数学试卷
,
1.D 2.C 3.C 4.A 5.B 6.B. 7.C 8.B
当 或 时, ,当 时, ,
9.AB 10.ABC
因此函数 在 上单调递增,在 上单调递减........................................................10'
【详解】对于A,由 ,得 ,∴ ,故A正确;
当 时, 取得极大值 ,当 时, 取得极小值 ,
所以函数 的递增区间为 ,递减区间为 ,
对于B, ,
极大值 ,极小值 ..................................................................................15'
当 时, ,当 时, ,
17.【答案】(1) , (2)
∴ 在 , 上单调递减,在 上单调递增,
∴ 是函数的极小值, 是函数的极大值,故B正确; 【详解】(1)由题意可知 , 当 时,
对于C,当 时, ,根据B可知,函数的最小值是 ,再根据单调性可知,当
累加得
时,方程 有且只有两个实根,所以C正确;
对于D:由图象可知,t的最大值是2,所以D不正确.
11. ACD
12.45 13. 14.3 当 时, 满足上式.
【详解】由 可知:
........................................................................................................4'
当 为偶数时, ,当 为奇数时, , . 当 时, ,且 ,
所以 ,
两式相减得 , ,即
即
,由此解得 . 数列 是首项为1,公比为 的等比数列, .............................................................7'
15.【答案】(1) (2)
(2)
【详解】(1)因为 ,所以数列 是以 为首项,3为公比
的等比数列,所以 ,所以
...................................................................................................6'
(2)因为 ,所以 ................................13' ②
16.【答案】(1) ;
①-②得
(2)递增区间为 ,递减区间为 ,极大值 ,极小值 .
【详解】(1)函数 ,求导得 ,当 时, ,则 在 上单调递增,
,
当 时, ,则 在 上单调递减,
...........................................15'
4 4
所以 ,即满足不等式成立的b≥ ,所以 的最小值为
e e
;.............................17'
4
18.【答案】(1)见解析 (2)
e
19.【答案】(1)数列 为周期数列,周期为2,(2) ,(3)不存在,理由见解析
【详解】
【详解】(1)因为 ,
,
所以数列 是周期数列,其最小正周期为2..............................................................................4'
(2)因为无穷数列 是周期为 的周期数列,且 , ,
所以当 为偶数时, ;
当 为奇数时, ,
因为 对一切正整数 恒成立,
所以当 为偶数时, ,故只需 即可;
.........................................8'
当 为奇数时, 恒成立,故只需 即可;
(2)当 时,不等式可化为 ,
变形为 综上, 对一切正整数 恒成立,常数 的取值范围为 .......................................................9'
同构函数 ,求导得 , (3)假设存在非零常数 ,使得 是周期为T的数列,所以 ,即 ,
所以 ,即 ,
所以 在 上是增函数,而原不等式可化为 ,
所以 ,即 ,
根据单调性可得: , 所以数列 是周期为 的周期数列,
因为 ,
再构造 ,则 ,即 ,因为 ,
所以 , ,
所以数列 的周期为 ,
所以 ,即 ,显然方程无解,
所以不存在非零常数 ,使得 是周期数列.......................17'