2004年河北高考理科数学真题及答案_数学高考真题试卷_旧1990-2007·高考数学真题_1990-2007·高考数学真题·PDF_河北

2004 年河北高考理科数学真题及答案 本试卷分第I卷（选择题）和第II卷（非选择题）两部分. 共150分. 考试时间120分钟. 第I卷（选择题 共60分） 参考公式： 球的表面积公式 如果事件A、B互斥，那么 S=4R2 P（A+B）=P（A）+P（B） 其中R表示球的半径， 如果事件A、B相互独立，那么 球的体积公式 P（A·B）=P（A）·P（B） 4 如果事件A在一次试验中发生的概率是P，那么 V= R3， 3 n次独立重复试验中恰好发生k次的概率 其中R表示球的半径 P(k)=Ck Pk(1－P)n－k n n 一、选择题 ：本大题共12小题，每小题6分，共60。 1．(1－i)2·i= （ ） A．2－2i B．2+2i C．－2 D．2 1x 2．已知函数 f(x) lg .若f(a) b.则f(a)  （ ） 1 x 1 1 A．b B．－b C． D．－ b b 3．已知a、b均为单位向量，它们的夹角为60°，那么|a+3b|= （ ） A． 7 B． 10 C． 13 D．4 4．函数y  x11(x 1)的反函数是 （ ） A．y=x2－2x+2(x<1) B．y=x2－2x+2(x≥1) C．y=x2－2x (x<1) D．y=x2－2x (x≥1) 1 5．(2x3  )7的展开式中常数项是 （ ） x A．14 B．－14 C．42 D．－42 6．设A、B、I均为非空集合，且满足AB I，则下列各式中错误的是 （ ） A．( A)∪B=I B．( A)∪( B)=I I I I C．A∩( B)= D．( A)∪( B)= B I I I I x2 7．椭圆  y2 1的两个焦点为F、F，过F 作垂直于x轴的直线与椭圆相交，一个交点 1 2 1 4 为P，则| PF |= （ ） 2 第1页 | 共12页3 7 A． B． 3 C． D．4 2 2 8．设抛物线y2=8x的准线与x轴交于点Q，若过点Q的直线l与抛物线有公共点，则直线l 的斜率的取值范围是 （ ） 1 1 A．[－ ， ] B．[－2，2] C．[－1，1] D．[－4，4] 2 2  9．为了得到函数y sin(2x )的图象，可以将函数y cos2x的图象 （ ） 6   A．向右平移 个单位长度 B．向右平移 个单位长度 6 3   C．向左平移 个单位长度 D．向左平移 个单位长度 6 3 10．已知正四面体ABCD的表面积为S，其四个面的中心分别为E、F、G、H.设四面体EFGH的表面积为T， T 则 等于 （ ） S 1 4 1 1 A． B． C． D． 9 9 4 3 11．从数字1，2，3，4，5，中，随机抽取3个数字（允许重复）组成一个三位数，其各位数字之和等于9 的概率为 （ ） 13 16 18 19 A． B． C． D． 125 125 125 125 12．a2 b2 1,b2 c2  2,c2 a2  2,则abbcca的最小值为 （ ） 1 1 1 1 A． 3－ B． － 3 C．－ － 3 D． + 3 2 2 2 2 第Ⅱ卷（非选择题 共90分） 二、填空题：本大题共4小题，每小题4分，共16分.把答案填在题中横线上. 13．不等式|x+2|≥|x|的解集是 . 14．由动点 P 向圆x2+y2=1 引两条切线 PA、PB，切点分别为 A、B，∠APB=60°，则动点 P 的轨迹方程 为 . 第2页 | 共12页15．已知数列{a}，满足a=1，a=a+2a+3a+…+(n－1)a (n≥2)，则{a}的通项 n 1 n 1 2 3 n－1 n 1, n=1, a= ,n≥2. n 16．已知a、b为不垂直的异面直线，α是一个平面，则a、b在α上的射影有可能是 . ①两条平行直线 ②两条互相垂直的直线 ③同一条直线 ④一条直线及其外一点 在一面结论中，正确结论的编号是 （写出所有正确结论的编号）. 三、解答题：本大题共6小题，共74分.解答应写出文字说明，证明过程或演算步骤. 17．（本小题满分12分） sin4 xcos4 xsin2 xcos2 x 求函数 f(x)  的最小正周期、最大值和最小值. 2sin2x 18．（本小题满分12分） 一接待中心有A、B、C、D四部热线电话，已知某一时刻电话A、B占线的概率均为0.5，电话C、D占 线的概率均为0.4，各部电话是否占线相互之间没有影响.假设该时刻有ξ部电话占线.试求随机变量ξ的概 率分布和它的期望. 第3页 | 共12页19．（本小题满分12分） 已知aR,求函数 f(x)  x2eax的单调区间. 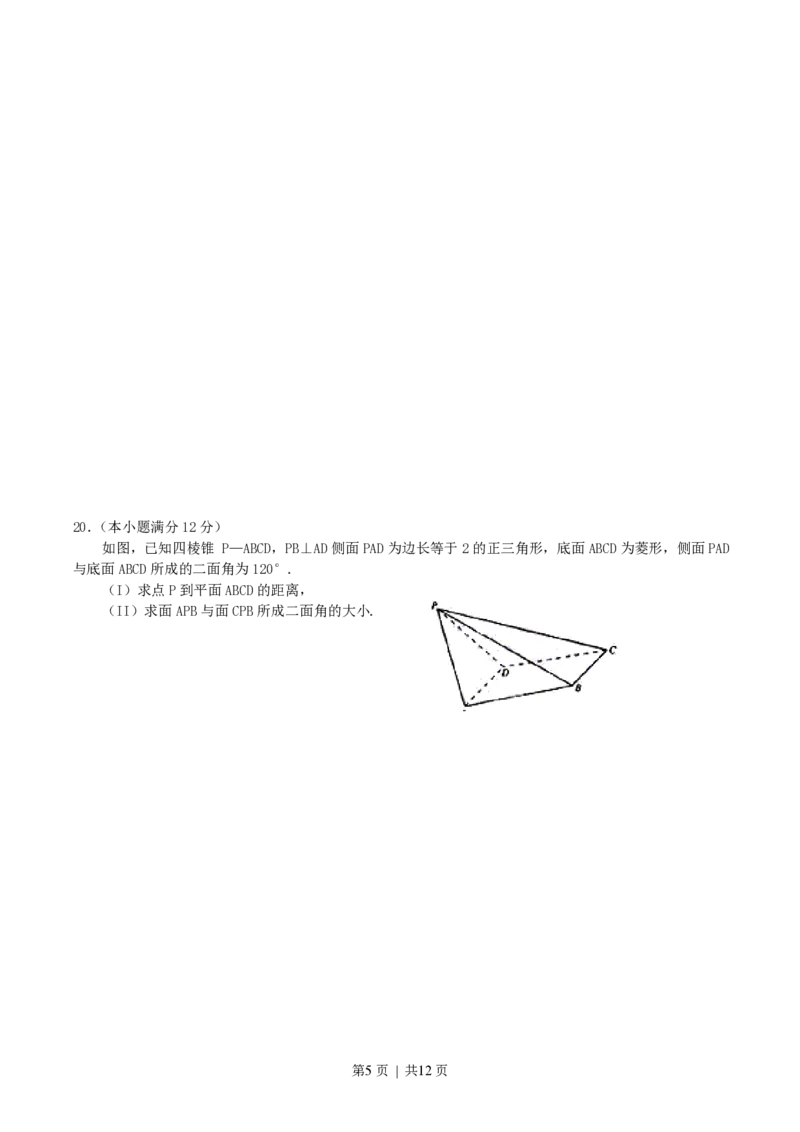第4页 | 共12页20．（本小题满分12分） 如图，已知四棱锥 P—ABCD，PB⊥AD侧面PAD为边长等于2的正三角形，底面ABCD为菱形，侧面PAD 与底面ABCD所成的二面角为120°. （I）求点P到平面ABCD的距离， （II）求面APB与面CPB所成二面角的大小. 第5页 | 共12页21．（本小题满分12分） x2 设双曲线C：  y2 1(a 0)与直线l:x y 1相交于两个不同的点A、B. a2 （I）求双曲线C的离心率e的取值范围： 5 （II）设直线l与y轴的交点为P，且PA PB.求a的值. 12 第6页 | 共12页22．（本小题满分14分） 已知数列{a }中a 1，且 n 1 a=a +(－1)K, 2k 2k－1 a =a+3k, 2k+1 2k 其中k=1,2,3,……. （I）求a, a； 3 5 （II）求{ a}的通项公式. n 第7页 | 共12页2004年高考理科数学答案 一、选择题 DBCBABCCBADB 二、填空题：本大题共4小题，每小题4分，共16分.把答案填在题中横线上. n! 13．{x|x≥－1} 14．x2+y2=4 15． 16．①②④ 2 三、解答题 17．本小题主要考查三角函数基本公式和简单的变形，以及三角函娄的有关性质.满分12分. (sin2 xcos2 x)2 sin2 xcos2 x 解： f(x)  22sinxcosx 1sin2 xcos2 x  2(1sinxcosx) 1  (1sinxcosx) 2 1 1  sin2x 4 2 3 1 所以函数f(x)的最小正周期是π，最大值是 ，最小值是 . 4 4 18．本小题主要考查离散型随机变量分布列和数学期望等概念.考查运用概率知识解决实际问题的能力.满 分12分. 解：P(ξ=0)=0.52×0.62=0.09. P(ξ=1)=C1 ×0.52×0.62+C1 ×0.52×0.4×0.6=0.3 2 2 P(ξ=2)= C2 ×0.52×0.62+C1 C1×0.52×0.4×0.6+C2 ×0.52×0.42=0.37. 2 2 2 2 P(ξ=3)= C2 C1×0.52×0.4×0.6+C1 C2×0.52×0.42=0.2 2 2 2 2 P(ξ=4)= 0.52×0.42=0.04 于是得到随机变量ξ的概率分布列为： ξ 0 1 2 3 4 P 0.09 0.3 0.37 0.2 0.04 所以Eξ=0×0.09+1×0.3+2×0.37+3×0.2+4×0.04=1.8. 19．本小题主要考查导数的概率和计算，应用导数研究函数性质的方法，考查分类讨论的数学思想.满分12 分. 解：函数f(x)的导数： f (x)  2xeax ax2eax (2xax2)eax. （I）当a=0时，若x<0，则 f (x)<0，若x>0,则 f (x)>0. 所以当a=0时，函数f(x)在区间（－∞，0）内为减函数，在区间（0，+∞）内为增函数. 2 （II）当a 0时,由2xax2 0,解得x   或x 0, a 第8页 | 共12页2 由2xax2 0,解得  x 0. a 2 2 所以，当a>0时，函数f(x)在区间（－∞，－ ）内为增函数，在区间（－ ，0）内为减函数，在 a a 区间（0，+∞）内为增函数； 2 （III）当a<0时，由2x+ax2>0，解得0－ . a 2 所以当a<0时，函数f(x)在区间（－∞，0）内为减函数，在区间（0，－ ）内为增函数，在区间 a 2 （－ ，+∞）内为减函数. a 20．本小题主要考查棱锥，二面角和线面关系等基本知识，同时考查空间想象能力和推理、运算能力.满分 12分. 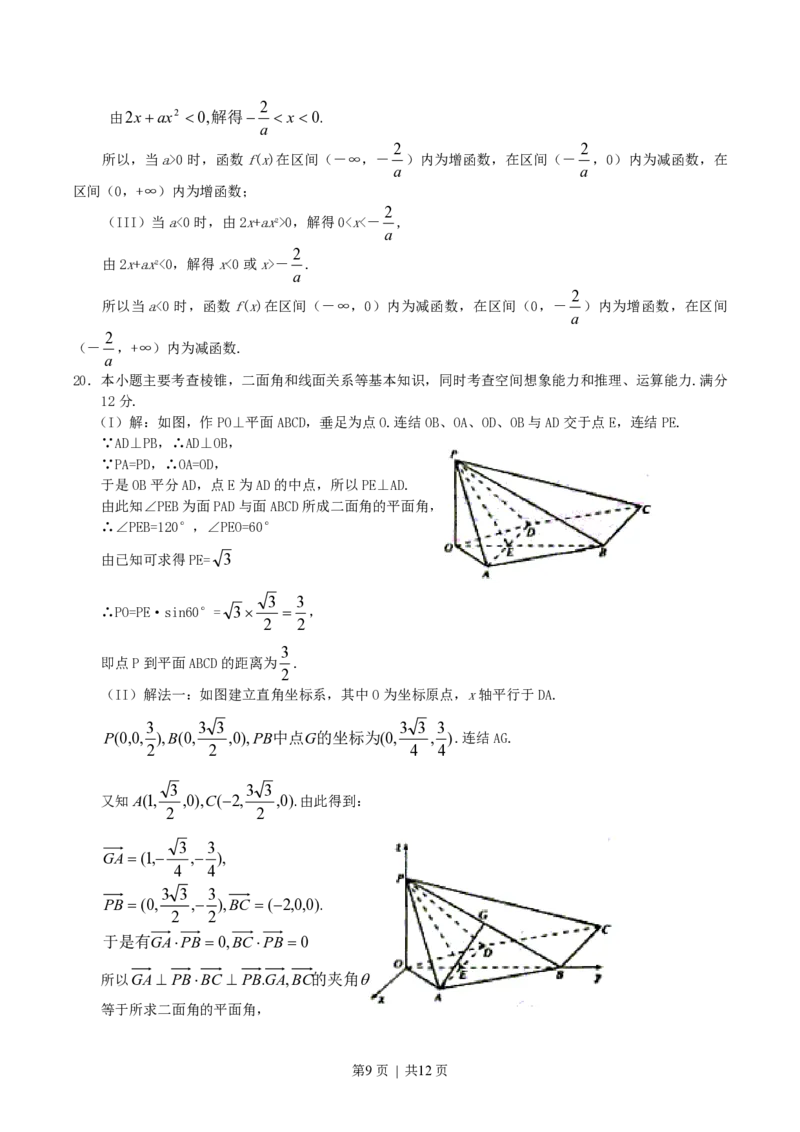（I）解：如图，作PO⊥平面ABCD，垂足为点O.连结OB、OA、OD、OB与AD交于点E，连结PE. ∵AD⊥PB，∴AD⊥OB， ∵PA=PD，∴OA=OD， 于是OB平分AD，点E为AD的中点，所以PE⊥AD. 由此知∠PEB为面PAD与面ABCD所成二面角的平面角， ∴∠PEB=120°，∠PEO=60° 由已知可求得PE= 3 3 3 ∴PO=PE·sin60°= 3  ， 2 2 3 即点P到平面ABCD的距离为 . 2 （II）解法一：如图建立直角坐标系，其中O为坐标原点，x轴平行于DA. 3 3 3 3 3 3 P(0,0, ),B(0, ,0),PB中点G的坐标为(0, , ).连结AG. 2 2 4 4 3 3 3 又知A(1, ,0),C(2, ,0).由此得到： 2 2 3 3 GA(1, , ), 4 4 3 3 3 PB (0, , ),BC (2,0,0). 2 2 于是有GAPB 0,BCPB 0 所以GA PBBC  PB.GA,BC的夹角 等于所求二面角的平面角， 第9页 | 共12页GABC 2 7 于是cos   , |GA|| BC | 7 2 7 所以所求二面角的大小为arccos . 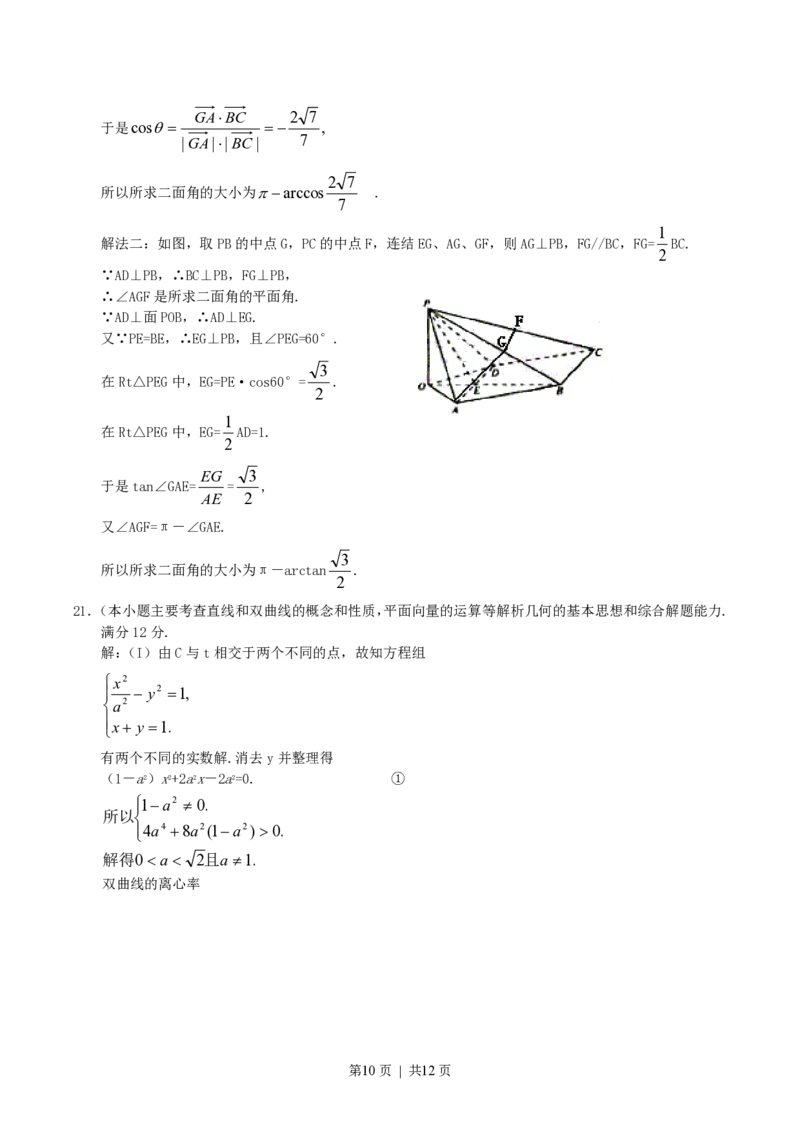7 1 解法二：如图，取PB的中点G，PC的中点F，连结EG、AG、GF，则AG⊥PB，FG//BC，FG= BC. 2 ∵AD⊥PB，∴BC⊥PB，FG⊥PB， ∴∠AGF是所求二面角的平面角. ∵AD⊥面POB，∴AD⊥EG. 又∵PE=BE，∴EG⊥PB，且∠PEG=60°. 3 在Rt△PEG中，EG=PE·cos60°= . 2 1 在Rt△PEG中，EG= AD=1. 2 EG 3 于是tan∠GAE= = , AE 2 又∠AGF=π－∠GAE. 3 所以所求二面角的大小为π－arctan . 2 21．（本小题主要考查直线和双曲线的概念和性质，平面向量的运算等解析几何的基本思想和综合解题能力. 满分12分. 解：（I）由C与t相交于两个不同的点，故知方程组 x2   y2 1, a2  x y 1. 有两个不同的实数解.消去y并整理得 （1－a2）x2+2a2x－2a2=0. ① 1a2  0. 所以   4a4 8a2(1a2) 0. 解得0 a  2且a 1. 双曲线的离心率 第10页 | 共12页1a2 1 e   1. a a2 0 a  2且a 1,  6 e  且e  2 2 6 即离心率e的取值范围为( , 2) ( 2,).  2 （II）设A(x ,y ),B(x ,y ),P(0,1) 1 1 2 2 5 PA PB,  12 5 (x ,y 1)  (x ,y 1). 1 1 12 2 2 5 由此得x  x . 1 12 2 由于x+x都是方程①的根，且1－a2≠0， 1 2 17 2a2 所以 x  . 12 2 1a2 5 2a2 x2  . 12 2 1a2 2a2 289 消去,x ,得  2 1a2 60 17 由a0,所以a 13 22．本小题主要考查数列，等比数列的概念和基本知识，考查运算能力以及分析、归纳和推理能力.满分14 分. 解：（I）a=a+(－1)1=0, 2 1 a=a+31=3. 3 2 a=a+(－1)2=4, 4 3 a=a+32=13, 5 4 所以，a=3,a=13. 3 5 (II) a =a+3k 2k+1 2k = a +(－1)k+3k, 2k－1 所以a －a =3k+(－1)k, 2k+1 2k－1 同理a －a =3k－1+(－1)k－1, 2k－1 2k－3 …… a－a=3+(－1). 3 1 所以(a －a )+(a －a )+…+(a－a) 2k+1 2k－1 2k－1 2k－3 3 1 =(3k+3k－1+…+3)+[(－1)k+(－1)k－1+…+(－1)], 3 1 由此得a －a= (3k－1)+ [(－1)k－1], 2k+1 1 2 2 第11页 | 共12页3k1 1 于是a =  (1)k 1. 2k+1 2 2 a= a +(－1)k 2k 2k－1 3k 1 =  (－1)k－1－1+(－1)k 2 2 3k 1 =  (－1)k=1. 2 2 {a}的通项公式为： n n1 3 2 n1 1 当n为奇数时，a= (1) 2  1; n 2 2 n 当n为偶数时， 32 n 1 a  (1)2  1. n 2 2 第12页 | 共12页