山西省长治市2024-2025学年高三上学期9月质量监测数学试题答案_2024-2025高三（6-6月题库）_2024年09月试卷_09232025山西三重教育高三9月质量检测（长治市高三9月质量监测）

长治市 2024-2025 学年度第一学期高三九月份质量监测
数学答案
一、ACBBC ADB 二、ABC AD ACD
三、12. 81 13. 2 3 14. e5
四、15.解：（1）由题及正弦定理得：2a2 (2bc)b(2cb)c,bc b2 c2 a2----2分
b2 c2 a2 1
cosA  ， -------------------------------------------4分
2bc 2
  
A0， ，A -------------------------------------------------6分
 2 3
 
0C 

 2  
（2）由△ABC为锐角三角形知， , C  ------8分
2  6 2

0 C 

 3 2
 3 3 
cosB2cosC co（s C）2cosC  cosC sinC  3sin（C ）--10分
3 2 2 3
  5 3 
C  ，  3sin（C ） 3-------------------12分
2 3 6 2 3
3
cosBcosC 的取值范围为（ ，3）-------------------13分
2
16.（1）MA平面ABC,BC 平面ABC,MA BC------------------2分
AB是圆的直径BC  AC, ------------------4分
MA AC  A,BC 平面MAC,------------------6分
BC 平面MBC,平面MBC 平面MAC------------------7分
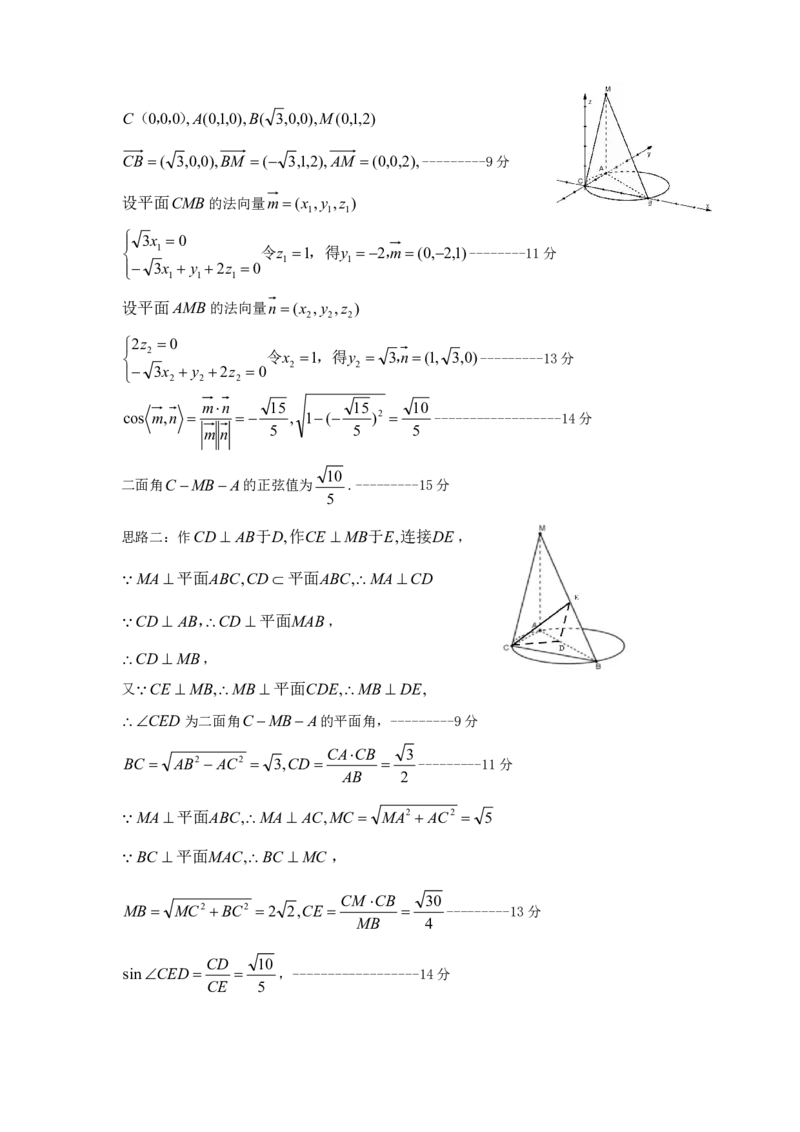
（ 2 ） 思 路 一 ： 如 图 ， 建 立 空 间 直 角 坐 标 系 Cxyz ，C（0，0，0）,A(0,1,0),B( 3,0,0),M(0,1,2)
CB ( 3,0,0),BM ( 3,1,2),AM (0,0,2),---------9分
设平面CMB的法向量m(x ,y ,z )
1 1 1
  3x 0

1 令z 1，得y 2，m(0,2,1)--------11分
1 1
   3x  y 2z 0
1 1 1
设平面AMB的法向量n(x ,y ,z )
2 2 2
2z 0
 2 令x 1，得y  3，n(1, 3,0)---------13分
  3x  y 2z 0 2 2
2 2 2
mn 15 15 10
cos m,n   , 1( )2  ------------------14分
m n 5 5 5
10
二面角CMB A的正弦值为 .---------15分
5
思路二：作CD  AB于D,作CE  MB于E,连接DE，
MA平面ABC,CD平面ABC,MACD
CD  AB，CD 平面MAB，
CD  MB，
又CE  MB,MB 平面CDE,MB  DE,
CED为二面角CMB A的平面角，---------9分
CACB 3
BC  AB2  AC2  3,CD   ---------11分
AB 2
MA平面ABC,MA AC,MC  MA2  AC2  5
BC 平面MAC,BC  MC ，
CM CB 30
MB  MC2 BC2 2 2,CE   ---------13分
MB 4
CD 10
sinCED   ，------------------14分
CE 510
二面角CMB A的正弦值为 .------------------15分
5
a 2
17.解：（1） f(x)  .------------------1分
x x2
由 曲 线 y  f(x)在点(1, f(1)) 处 的 切 线 与 直 线 x2y  0 垂 直 得 ，
f(1)a22------------------3分
a 0------------------4分
（2） f(x)的定义域为{x| x  0},.c------------------5分
ax2
om f(x) /.Com]
x2
当a  0时， f(x)0, f(x)在(0,)上是增函数；/]c------------------7分
2
当a0时,由f(x)0,得x
a
2
当x(0, )时, f(x)0, f(x)单调递增，
a
2
当x( ,)时, f(x)0, f(x)单调递减；------------------9分
a
综上，当a  0时， f(x)在(0,)上是增函数；
2 2
当a0时， f(x)在(0, )单调递增， f(x)在 ( ,)单调递减.
a a
2
（3）当a 2时， f(x1)2ln(x1) ,------------------10分
x1
2
令g(x) f(x1)4x102ln(x1) 4x10，x1,-----------------11分
x1
2 2 2(2x1)(x2)
g(x)  4 ------------------13分
x1 (x1)2 (x1)2
当x(1，2)时,g(x)0,g(x)单调递增；当x(2，)时,g(x)0,g(x)单调递减.
g(x) g(2)0，------------------14分
 f(x1)4x10.------------------15分
18.解：（1）由题得a2 b2 9，------------------1分
  x2 y2 12 3
将 2 3，3 代入  1得：  1
b2 9 b2 b2 9 b2b4 6b2 270,(b2 9)(b2 3)0,b2 9,a2 18------------------4分
x2 y2
椭圆E的方程为  1------------------5分
18 9
（2）设A(x ,y ),B(x ,y )，
1 1 2 2
x 2 y 2 x 2 y 2 x 2 x 2 y 2  y 2
1  1 1，2  2 1，两式相减得：1 2  1 2 ----------------6分
18 9 18 9 18 9
y  y （9 x x） 1
1 2  1 2  ------------------8分
x x 1（8 y  y） 2
1 2 1 2
1
l方程为y1 (x1),即x2y30------------------10分
2
y k(x3)

（3）由x2 y2 得：（12k2)x2 12k2x18k2 180

 1
18 9
12k2 18k2 18
x x  ,x x  ------------------12分
1 2 12k2 1 2 12k2
y  y 9y 3y 9k(x 3) 3k(x 3)
1 2  y  2  1  y x  2  1 k(x 3)x
2 1 y 2 2 2 1 2 2 2 1
k k   2  
AR FQ 6x 3 3(6x ) 3(6x )
1 1 1
9 54k2 18k2 18 1836k2
k（ （x x）x x 18） k（   ）
2 1 2 1 2 12k2 12k2 12k2
  0，------16分
3(6x ) 3(6x )
1 1
AR//FQ,又AF与RQ不平行，四边形ARQF 为梯形.------------------17分
19.（1）x2050.12550.23050.453550.24050.05300-----2分
0.95450.6827
（2）（ i ）P（250.25 X 399.5)0.6827 0.8186------5分
2
（
ii
）Z 服从二项分布B(20,0.8186），E(Z)200.818616.372------7分
1 1 1
（3）当3n59时，P  P  P ，P P  （P P ）------9分
n 2 n1 2 n2 n n1 2 n1 n2
1 1 1 1 3 1
P  ，P     ，P P  ------10分
1 2 2 2 2 2 4 2 1 41 1
  P P （ 2n59)是以 为首项， 为公比的等比数列，------11分
n n1 4 2
n2
1  1
P P    (2n59)
n n1 4  2
n2
1 1  1 1  1
P P  ，P P   ，...,P P    (2n59)
2 1 4 3 2 4  2 n n1 4  2
累加得：
 n1
1  1
 1  
4    2   2 1  1 n1 1 1 1 1 58
P P  ,P     (2n59),P  P    
n 1 1 n 3 6  2 60 2 58 3 6 2
1
2
 n1
2 1  1
    ，1n59
3 6  2
P 
n 58 ------15分
1 1 1
   ，n60

3 6 2
58  58
1 1 1 1 1
P P       1  0,P  P ------17分
59 60 3 3 2 3  2  59 60
 
注 ： 比 较 P 和 P 的 另 一 个 过 程 ：
59 60
58
2 1 1 2 1 1 1
P        ,P 1P   P
59 3 6 2 3 6 2 60 59 2 59