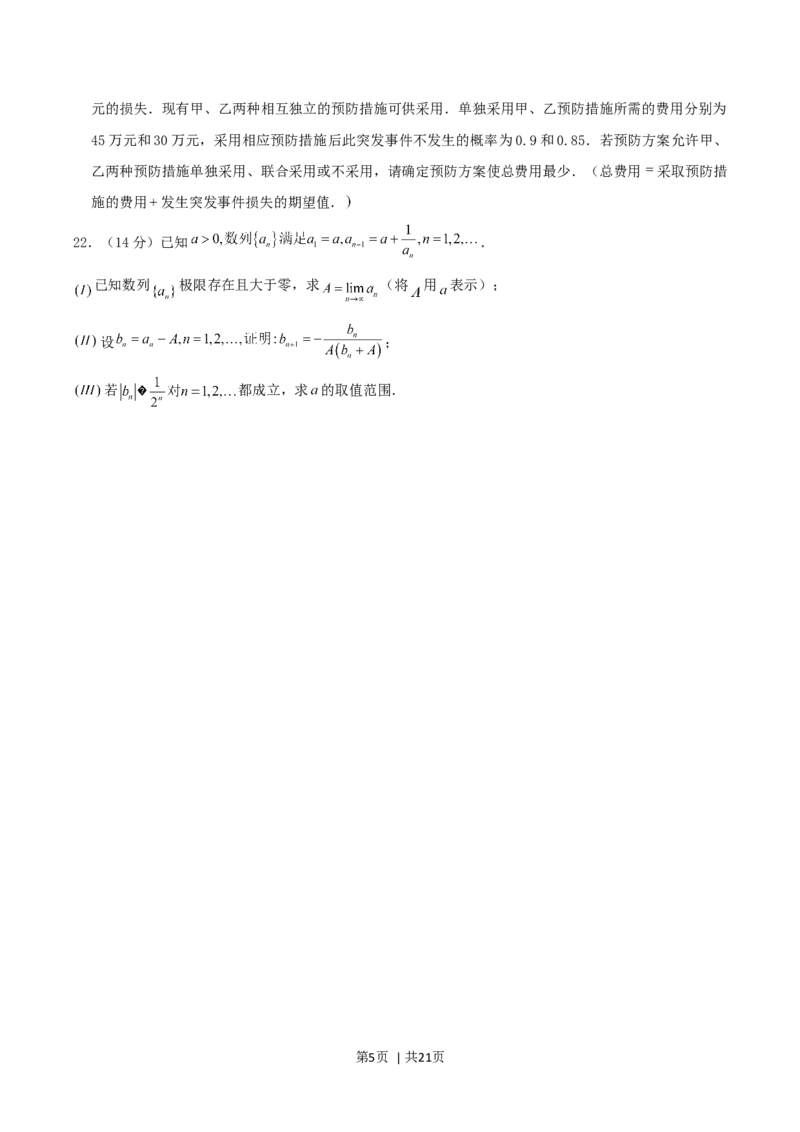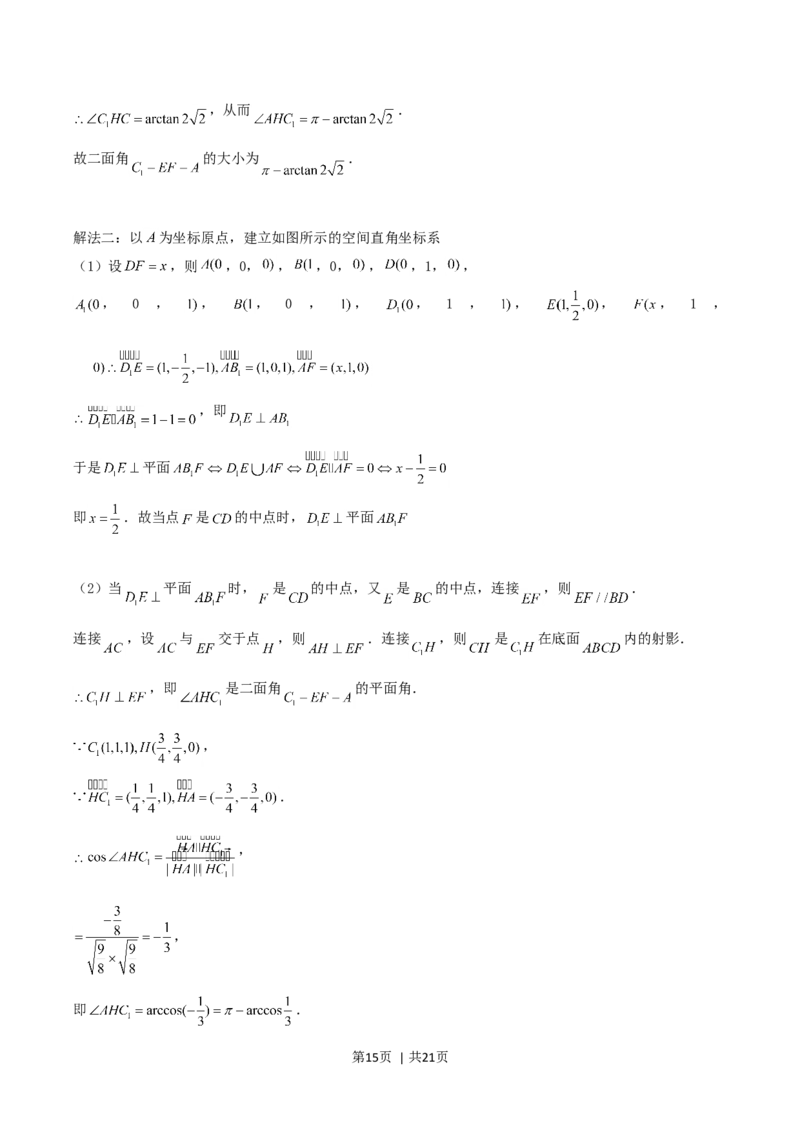2004年湖北高考理科数学真题及答案_数学高考真题试卷_旧1990-2007·高考数学真题_1990-2007·高考数学真题·word_湖北

2004 年湖北高考理科数学真题及答案 一、选择题（共12小题，每小题5分，满分60分） 1．（5分）与直线 的平行的抛物线 的切线方程是 A． B． C． D． 2．（5分）复数 的值是 A． B．16 C． D． 3．（5分）已知 ，则 的解析式为 A． B． C． D． 4．（5分）已知 为非零的平面向量．甲： ，乙： ，则 A．甲是乙的充分条件但不是必要条件 B．甲是乙的必要条件但不是充分条件 C．甲是乙的充要条件 D．甲既不是乙的充分条件也不是乙的必要条件 5．（5分）若 ，则下列不等式 ① ； ② ； ③ ； ④ 中，正确的不等式有 A．0个 B．1个 C．2个 D．3个 6．（5分）已知椭圆 的左、右焦点分别为 、 ，点 在椭圆上．若 、 、 是一个直角 三角形的三个顶点，则点 到 轴的距离为 第1页 | 共21页A． B．3 C． D． 7．（5分）函数 在 ， 上的最大值与最小值的和为 ，则 的值为 A． B． C．2 D．4 8．（5分）已知数列 的前 项和 ，其中 、 是非零常 数，则存在数列 、 使得 A． ，其中 为等差数列， 为等比数列 B． ，其中 和 都为等差数列 C． ，其中 为等差数列， 都为等比数列 D． ，其中 和 都为等比数列 9．（5分）函数 有极值的充要条件是 A． B． C． D． 10．（5分）设集合 ， 对任意实数 恒成立 ，则下列关系 中成立的是 A． B． C． D． 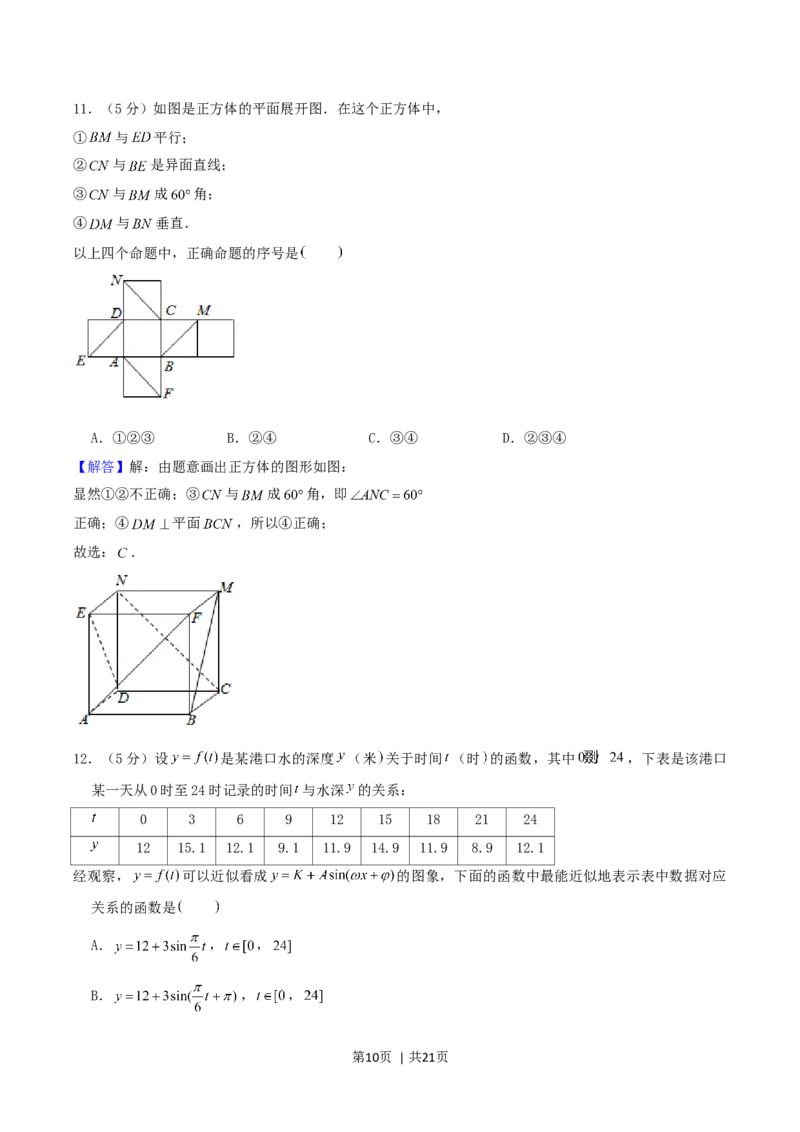11．（5分）如图是正方体的平面展开图．在这个正方体中， ① 与 平行； ② 与 是异面直线； ③ 与 成 角； ④ 与 垂直． 以上四个命题中，正确命题的序号是 第2页 | 共21页A．①②③ B．②④ C．③④ D．②③④ 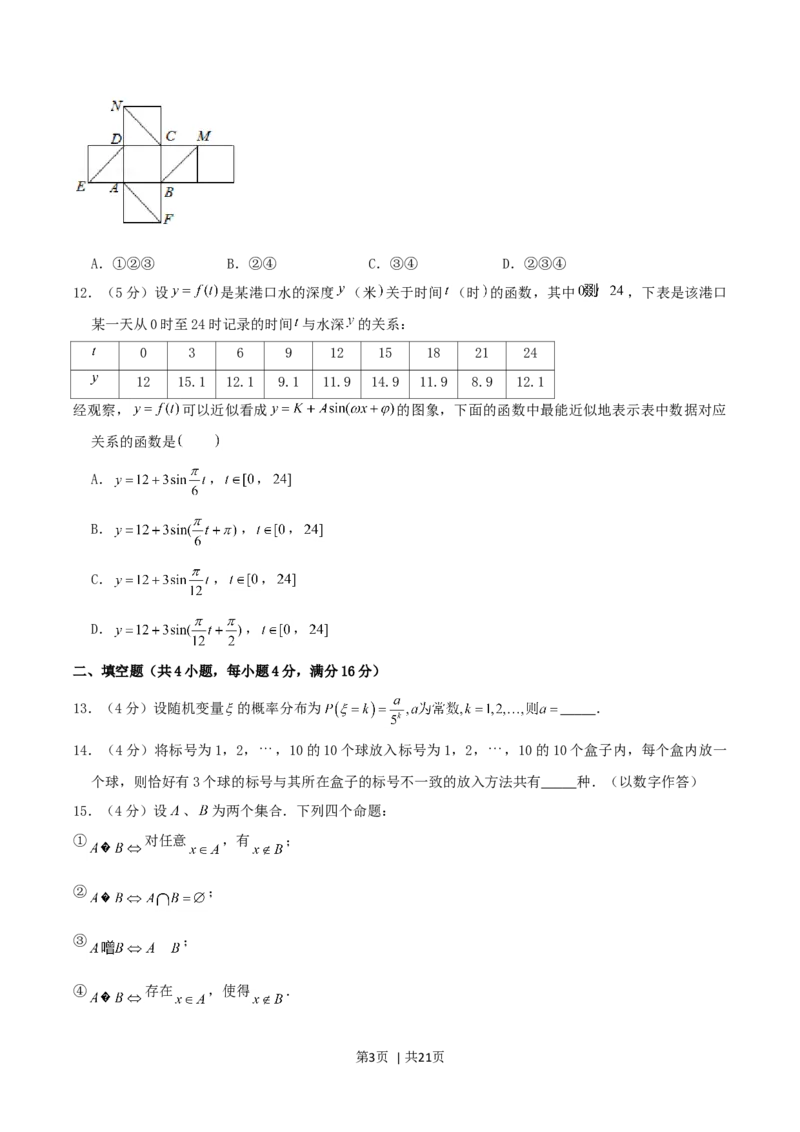12．（5分）设 是某港口水的深度 （米 关于时间 （时 的函数，其中 ，下表是该港口 某一天从0时至24时记录的时间 与水深 的关系： 0 3 6 9 12 15 18 21 24 12 15.1 12.1 9.1 11.9 14.9 11.9 8.9 12.1 经观察， 可以近似看成 的图象，下面的函数中最能近似地表示表中数据对应 关系的函数是 A． ， ， B． ， ， C． ， ， D． ， ， 二、填空题（共4小题，每小题4分，满分16分） 13．（4分）设随机变量 的概率分布为 ． 14．（4分）将标号为1，2， ，10的10个球放入标号为1，2， ，10的10个盒子内，每个盒内放一 个球，则恰好有3个球的标号与其所在盒子的标号不一致的放入方法共有 种．（以数字作答） 15．（4分）设 、 为两个集合．下列四个命题： ① 对任意 ，有 ； ② ； ③ ； ④ 存在 ，使得 ． 第3页 | 共21页其中真命题的序号是 ．（把符合要求的命题序号都填上） 16．（4分）某日中午12时整，甲船自 处以 的速度向正东行驶，乙船自 的正北 处以 的速度向正南行驶，则当日12时30分时两船之间距间对时间的变化率是 ． 三、解答题（共6小题，满分74分） 17．（12分）已知 ， ， ，求 的值． 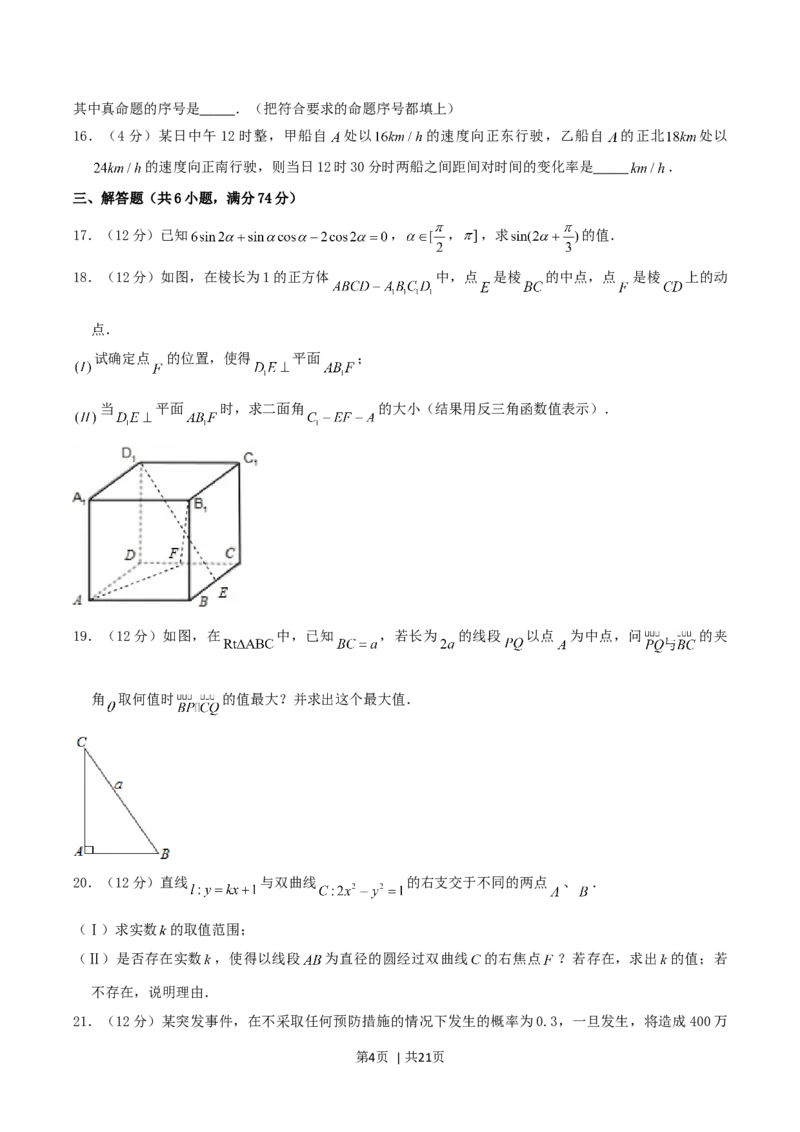18．（12分）如图，在棱长为1的正方体 中，点 是棱 的中点，点 是棱 上的动 点． 试确定点 的位置，使得 平面 ； 当 平面 时，求二面角 的大小（结果用反三角函数值表示）． 19．（12分）如图，在 中，已知 ，若长为 的线段 以点 为中点，问 的夹 角 取何值时 的值最大？并求出这个最大值． 20．（12分）直线 与双曲线 的右支交于不同的两点 、 ． （Ⅰ）求实数 的取值范围； （Ⅱ）是否存在实数 ，使得以线段 为直径的圆经过双曲线 的右焦点 ？若存在，求出 的值；若 不存在，说明理由． 21．（12分）某突发事件，在不采取任何预防措施的情况下发生的概率为0.3，一旦发生，将造成400万 第4页 | 共21页元的损失．现有甲、乙两种相互独立的预防措施可供采用．单独采用甲、乙预防措施所需的费用分别为 45万元和30万元，采用相应预防措施后此突发事件不发生的概率为0.9和0.85．若预防方案允许甲、 乙两种预防措施单独采用、联合采用或不采用，请确定预防方案使总费用最少．（总费用 采取预防措 施的费用 发生突发事件损失的期望值． 22．（14分）已知 ． 已知数列 极限存在且大于零，求 （将 用 表示）； 设 ； 若 都成立，求 的取值范围． 第5页 | 共21页2004年湖北省高考数学试卷（理科） 参考答案与试题解析 一、选择题（共12小题，每小题5分，满分60分） 1．（5分）与直线 的平行的抛物线 的切线方程是 A． B． C． D． 【解答】解：由题意可设切线方程为 联立方程组 得 △ 解得 ， 切线方程为 ， 故选： ． 2．（5分）复数 的值是 A． B．16 C． D． 【解答】解：复数 故选： ． 3．（5分）已知 ，则 的解析式为 A． B． C． D． 【解答】解：令 ， 得 ， ， 第6页 | 共21页． 故选： ． 4．（5分）已知 为非零的平面向量．甲： ，乙： ，则 A．甲是乙的充分条件但不是必要条件 B．甲是乙的必要条件但不是充分条件 C．甲是乙的充要条件 D．甲既不是乙的充分条件也不是乙的必要条件 【解答】解：命题甲： （舍去）或 或 ． 命题乙： ，因而乙 甲，但甲 乙． 故甲是乙的必要条件但不是充分条件． 故选： ． 5．（5分）若 ，则下列不等式 ① ； ② ； ③ ； ④ 中，正确的不等式有 A．0个 B．1个 C．2个 D．3个 【解答】解： ， ， ，故①正确． ，则 ，故②错误． ③显然错误． 由于 ， ， ，故④正确． 综上，①④正确，②③错误， 故选： ． 6．（5分）已知椭圆 的左、右焦点分别为 、 ，点 在椭圆上．若 、 、 是一个直角 三角形的三个顶点，则点 到 轴的距离为 A． B．3 C． D． 第7页 | 共21页【解答】解：设椭圆短轴的一个端点为 ． 由于 ， ， ， 只能 或 ． 令 得 ， ． 即 到 轴的距离为 ， 故选： ． 7．（5分）函数 在 ， 上的最大值与最小值的和为 ，则 的值为 A． B． C．2 D．4 【解答】解： 是 ， 上的增函数或减函数， 故 （1） ，即 ， ． 故选： ． 8．（5分）已知数列 的前 项和 ，其中 、 是非零常 数，则存在数列 、 使得 A． ，其中 为等差数列， 为等比数列 B． ，其中 和 都为等差数列 第8页 | 共21页C． ，其中 为等差数列， 都为等比数列 D． ，其中 和 都为等比数列 【解答】解：当 时， ，当 时， ， 故选： ． 9．（5分）函数 有极值的充要条件是 A． B． C． D． 【解答】解：当 时，函数 是单调增函数无极值，故排除 ， 当 时，函数 是单调增函数无极值，故排除 ， 故选： ． 10．（5分）设集合 ， 对任意实数 恒成立 ，则下列关系 中成立的是 A． B． C． D． 【解答】解： 对任意实数 恒成立 ， 对 分类：① 时， 恒成立； ② 时，需△ ，解得 ． 综合①②知 ， ． ， 故选： ． 第9页 | 共21页11．（5分）如图是正方体的平面展开图．在这个正方体中， ① 与 平行； ② 与 是异面直线； ③ 与 成 角； ④ 与 垂直． 以上四个命题中，正确命题的序号是 A．①②③ B．②④ C．③④ D．②③④ 【解答】解：由题意画出正方体的图形如图： 显然①②不正确；③ 与 成 角，即 正确；④ 平面 ，所以④正确； 故选： ． 12．（5分）设 是某港口水的深度 （米 关于时间 （时 的函数，其中 ，下表是该港口 某一天从0时至24时记录的时间 与水深 的关系： 0 3 6 9 12 15 18 21 24 12 15.1 12.1 9.1 11.9 14.9 11.9 8.9 12.1 经观察， 可以近似看成 的图象，下面的函数中最能近似地表示表中数据对应 关系的函数是 A． ， ， B． ， ， 第10页 | 共21页C． ， ， D． ， ， 【解答】解：排除法： 可以近似看成 的图象， 由 可排除 、 ， 将 代入 排除 ． 故选： ． 二、填空题（共4小题，每小题4分，满分16分） 13．（4分）设随机变量 的概率分布为 4 ． 【解答】解： 由题意知根据所有的概率和为 把 提出 括号中为无穷等比数列，根据无穷等比递缩数列的求和公式得到 故答案为：4 14．（4分）将标号为1，2， ，10的10个球放入标号为1，2， ，10的10个盒子内，每个盒内放一 个球，则恰好有3个球的标号与其所在盒子的标号不一致的放入方法共有 24 0 种．（以数字作答） 【解答】解：由分步计数原理知 从10个盒中挑3个与球标号不一致，共 种挑法， 每一种3个盒子与球标号全不一致的方法为2种， 共有 种． 故答案为：240． 15．（4分）设 、 为两个集合．下列四个命题： ① 对任意 ，有 ； 第11页 | 共21页② ； ③ ； ④ 存在 ，使得 ． 其中真命题的序号是 ④ ．（把符合要求的命题序号都填上） 【解答】解：如下图所示： 存在 ，有 结合图象可得①错误；②错误；④正确． 对③判断如下图所示． 与 不存在必然的关系，故③错误． 故答案为：④ 16．（4分）某日中午12时整，甲船自 处以 的速度向正东行驶，乙船自 的正北 处以 的速度向正南行驶，则当日12时30分时两船之间距间对时间的变化率是 ． 【解答】解： 甲船自 处以 的速度向正东行驶，乙船自 的正北 处以 的速度向正 南 行 驶 ， 当 日 12 时 30 分 时 ， 甲 船 没 有 到 达 处 ， 故 甲 乙 两 船 之 间 的 距 离 函 数 是 当日12时30分时， ， 第12页 | 共21页此时两船之间距间对时间的变化率是 故答案为： ． 三、解答题（共6小题，满分74分） 17．（12分）已知 ， ， ，求 的值． 【解答】解： ， ， ， ， ， ， ， ， ． 18．（12分）如图，在棱长为1的正方体 中，点 是棱 的中点，点 是棱 上的动 点． 试确定点 的位置，使得 平面 ； 当 平面 时，求二面角 的大小（结果用反三角函数值表示）． 第13页 | 共21页【解答】解法一： 连接 ，则 是 在面 ；内的射影 ， ， 于是 平面 ． 连接 ，则 是 在底面 内的射影． ． 是正方形， 是 的中点． 当且仅当 是 的中点时， ， 即当点 是 的中点时， 平面 ．（6分） 当 平面 时，由 知点 是 的中点． 又已知点 是 的中点，连接 ，则 ．连接 ， 设 与 交于点 ，则 ，连接 ，则 是 在底面 内的射影． ，即 是二面角 的平面角． 在 △ 中， ， ， ． 第14页 | 共21页，从而 ． 故二面角 的大小为 ． 解法二：以 为坐标原点，建立如图所示的空间直角坐标系 （1）设 ，则 ，0， ， ，0， ， ，1， ， ， 0 ， ， ， 0 ， ， ， 1 ， ， ， ， 1 ， ，即 于是 平面 即 ．故当点 是 的中点时， 平面 （2）当 平面 时， 是 的中点，又 是 的中点，连接 ，则 ． 连接 ，设 与 交于点 ，则 ．连接 ，则 是 在底面 内的射影． ，即 是二面角 的平面角． ， ． ， ， 即 ． 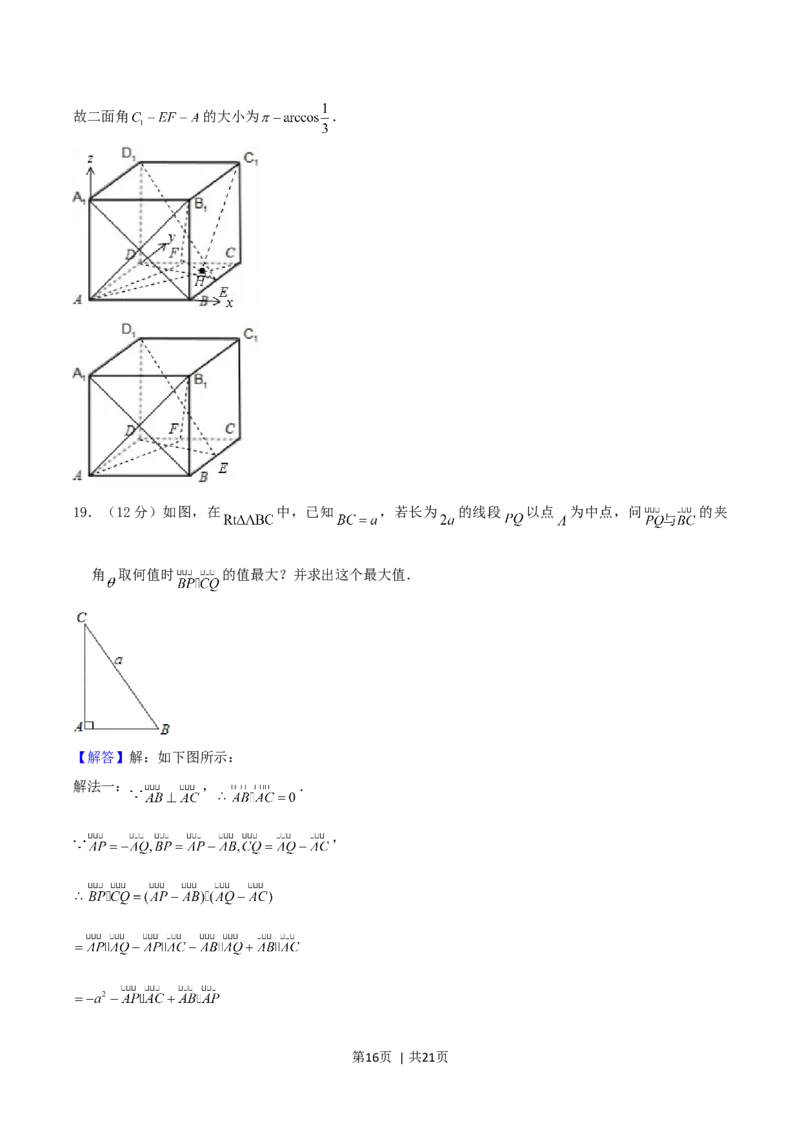第15页 | 共21页故二面角 的大小为 ． 19．（12分）如图，在 中，已知 ，若长为 的线段 以点 为中点，问 的夹 角 取何值时 的值最大？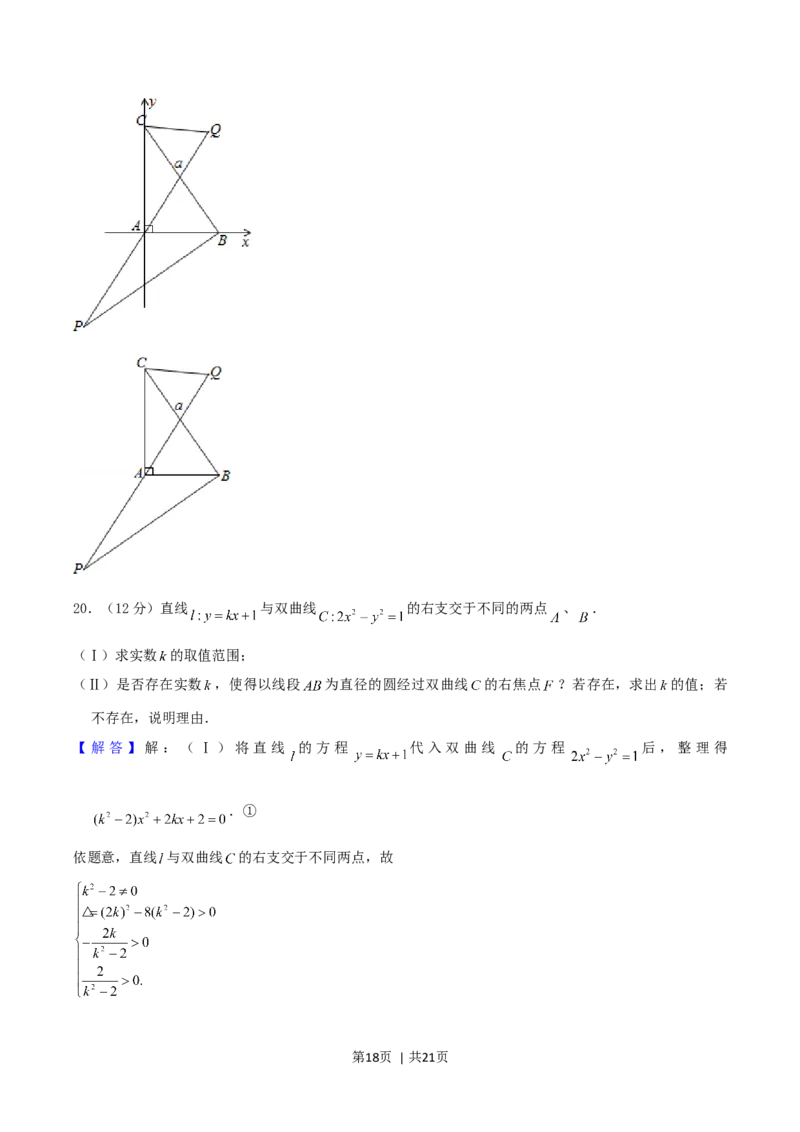并求出这个最大值． 【解答】解：如下图所示： 解法一： ， ． ， 第16页 | 共21页． 故当 ，即 与 方向相同）时， 最大．其最大值为0． 解法二：以直角顶点 为坐标原点，两直角边所在直线为坐标轴建立如图所示的平面直角坐标系． 设 ，则 ， ， ， 且 ， ． 设点 的坐标为 ，则 ． ， ． ． ． ． ． 故当 ， 即 与 方向相同）时， 最大，其最大值为0． 第17页 | 共21页20．（12分）直线 与双曲线 的右支交于不同的两点 、 ． （Ⅰ）求实数 的取值范围； （Ⅱ）是否存在实数 ，使得以线段 为直径的圆经过双曲线 的右焦点 ？若存在，求出 的值；若 不存在，说明理由． 【解答】解：（Ⅰ）将直线 的方程 代入双曲线 的方程 后，整理得 ．① 依题意，直线 与双曲线 的右支交于不同两点，故 第18页 | 共21页解得 的取值范围是 ． （Ⅱ）设 、 两点的坐标分别为 ， 、 ， ，则由①式得 ② 假设存在实数 ，使得以线段 为直径的圆经过双曲线 的右焦点 ． 则由 得： ． 即 ． 整理得 ．③ 把②式及 代入③式化简得 ． 解得 可知 使得以线段 为直径的圆经过双曲线 的右焦点． 21．（12分）某突发事件，在不采取任何预防措施的情况下发生的概率为0.3，一旦发生，将造成400万 元的损失．现有甲、乙两种相互独立的预防措施可供采用．单独采用甲、乙预防措施所需的费用分别为 45万元和30万元，采用相应预防措施后此突发事件不发生的概率为0.9和0.85．若预防方案允许甲、 乙两种预防措施单独采用、联合采用或不采用，请确定预防方案使总费用最少．（总费用 采取预防措 施的费用 发生突发事件损失的期望值． 【解答】解：①不采取预防措施时，总费用即损失期望为 （万元）； ②若单独采取措施甲，则预防措施费用为45万元，发生突发事件的概率为 ，损失期望值为 （万元），所以总费用为 （万元） ③若单独采取预防措施乙，则预防措施费用为30万元，发生突发事件的概率为 ，损失期望 值为 （万元），所以总费用为 （万元）； ④若联合采取甲、乙两种预防措施，则预防措施费用为 （万元），发生突发事件的概率为 ，损失期望值为 （万元），所以总费用为 （万元）． 综合①、②、③、④，比较其总费用可知，应选择联合采取甲、乙两种预防措施，可使总费用最少． 22．（14分）已知 ． 第19页 | 共21页已知数列 极限存在且大于零，求 （将 用 表示）； 设 ； 若 都成立，求 的取值范围． 【 解 答 】 解 ： 由 ， ． ． ． ． ． ． ． 当 时结论成立（已验证）． 假设当 故只须证明 ． ， ， ． 第20页 | 共21页． ． 即 时结论成立． 根据 和 可知结论对一切正整数都成立． 故 ． 声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布 日期：2019/5/23 23:08:08；用户：15217760367；邮箱：15217760367；学号：10888156 第21页 | 共21页