文档内容
重庆乌江新高考协作体 2024 届高考模拟监测(二)
数学答案
(分数:150分,时间:120分钟)
1-4.BBCA 5-8.ABDB
9.BCD
10.AD
11.AB
12.
13. /
14. .
15.(1)由于 ,则切点坐标为 ,
因为 ,所以切线斜率为 ,
故切线方程为 ;
(2)当 时, 等价于 ,
令 , ,
恒成立,则 恒成立, ,
当 时, ,函数 在 上单调递减, ,不符合题意;当 时,由 ,得 ,
时, ,函数 单调递减, ,不符合题意;
当 时, ,因为 ,所以 ,则 ,
所以函数 在 上单调递增 ,符合题意.
综上所述, ,所以 的取值范围为 .
16.(1) ,由正弦定理得 ,
则 ,
即 则 ,
且 , , ;
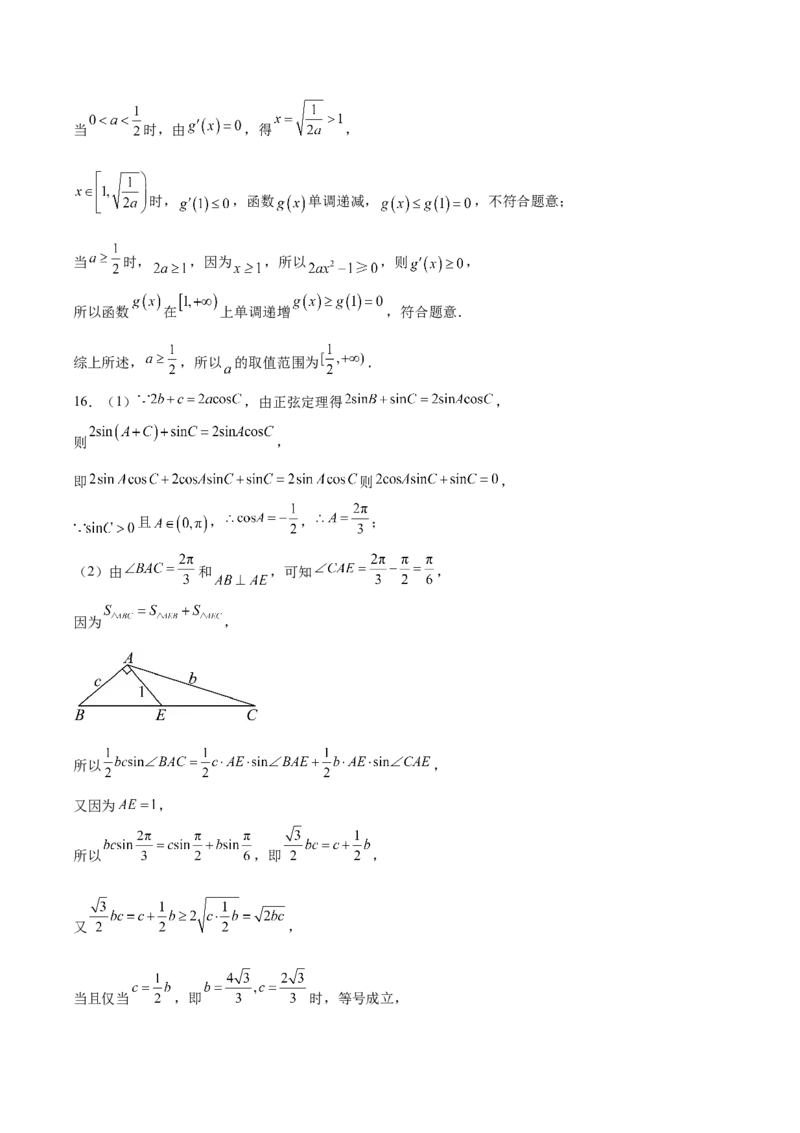
(2)由 和 ,可知 ,
因为 ,
所以 ,
又因为 ,
所以 ,即 ,
又 ,
当且仅当 ,即 时,等号成立,所以 ,
所以 ,
所以△ABC的面积的最小值为 .
17.(1) 的所有可能取值为 .
,
,
所以 的分布列为
-1 0 1
(2)①由题意,
得 ,所以
所以 ,
又 ,
所以所以
,
所以 ,
②记“该型号汽车启动自动驾驶功能后无需自动切换到另一个自动驾驶系统”为事件 ,“该型号汽车启
动自动驾驶功能后先启动系统 ”为事件 ,
因为 ,
所以由题意,得 ,
,
所以
,
即该型号汽车启动自动驾驶功能后无需自动切换到另一个自动驾驶系统的概率为0.9988.
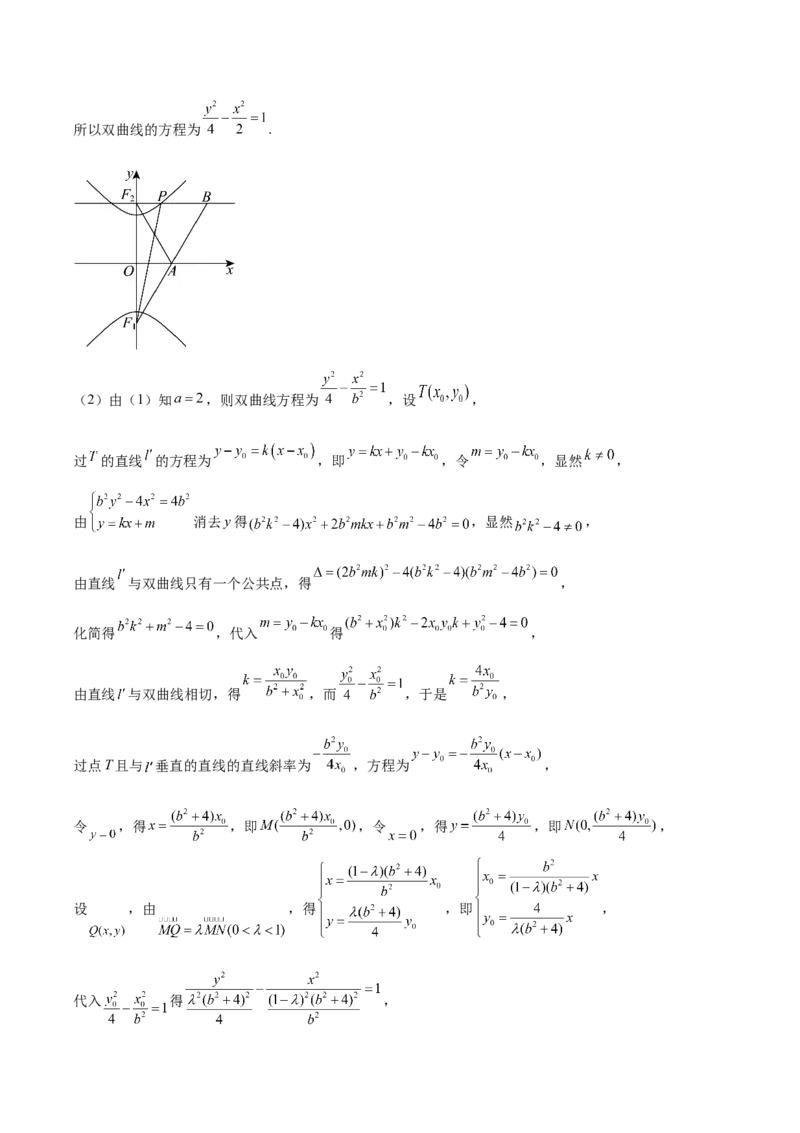
18.(1)依题意,
,解得 ,又双曲线的一条渐近线为 ,则 ,即 ,所以双曲线的方程为 .
(2)由(1)知 ,则双曲线方程为 ,设 ,
过 的直线 的方程为 ,即 ,令 ,显然 ,
由 消去y得 ,显然 ,
由直线 与双曲线只有一个公共点,得 ,
化简得 ,代入 得 ,
由直线 与双曲线相切,得 ,而 ,于是 ,
过点T且与 垂直的直线的直线斜率为 ,方程为 ,
令 ,得 ,即 ,令 ,得 ,即 ,
设 ,由 ,得 ,即 ,
代入 得 ,依题意,该双曲线与双曲线 共焦点,则 ,
化简得 ,于是 ,
,当且仅当 , 时取等号,
所以 的最大值为1.
19.(1)椭圆 的标准方程为 ,则 .
当直线 的倾斜角为 时, 分别为椭圆的左、右顶点,此时两切线平行无交点,不符合题意,
所以直线 的倾斜角不为 ,
设直线 ,
由 ,得 ,
则 ,
所以,
又椭圆 在点 处的切线方程为 ,在点 处的切线方程为 ,
由 ,得 ,
代入 ,得 ,所以 ,
则点 到直线 的距离 ,
所以 ,
设 ,则 ,
令 ,则 ,所以 在 上单调递增,
所以当 ,即 时, 的面积最小,最小值是 ;
(2)椭圆 的焦点在 轴上,长半轴长为 ,短半轴长为1,
椭球由椭圆 及其内部绕 轴旋转 而成旋转体,
构造一个底面半径为1,高为 的圆柱,在圆柱中挖去一个以圆柱下底面圆心为顶点,
圆柱上底面为底面的圆锥后得到一新几何体,当平行于底面的截面与圆锥顶点距离为 时,设小圆锥底面半径为 ,
则 ,即 ,所以新几何体的截面面积为 ,
把 代入 ,得 ,解得 ,
所以半椭球的截面面积为 ,
由祖暅原理,得椭球的体积 .