2005年上海高考数学试卷（文）（自主命题）（空白卷）_数学高考真题试卷_旧1990-2007·高考数学真题_1990-2007·高考数学真题·PDF_上海

绝密★启用前 2005年普通高等学校招生全国统一考试（上海卷） 数学试卷(文史类) （满分150分，考试时间120分钟） 考生注意 1.本场考试时间120分钟，试卷共4页，满分150分，答题纸共2页. 2.作答前，在答题纸正面填写姓名、准考证号，反面填写姓名，将核对后的条形码贴在答 题纸指定位置. 3.所有作答务必填涂或书写在答题纸上与试卷题号对应的区域，不得错位.在试卷上作答 一律不得分. 4.用2B铅笔作答选择题，用黑色字迹钢笔、水笔或圆珠笔作答非选择题. 一、填空题（本大题满分48分）本大题共有12题，只要求直接填写结果，每个空格填对得4 分，否则一律得零分. 1．函数 f(x) log (x1)的反函数 f 1(x)=__________. 4 2．方程4x 2x 20的解是__________. 3．若x,y满足条件x y3，则z 3x4y的最大值是__________.   y2x 4．直角坐标平面xoy中，若定点A(1,2)与动点P(x,y)满足OPOA 4，则点P的轨迹 方程是__________. 5．函数y cos2xsinxcosx的最小正周期T=__________. 1     6．若cos ，0, ，则cos =__________. 7  2  3   7．若椭圆长轴长与短轴长之比为2，它的一个焦点是 2 15,0 ，则椭圆的标准方程是____ ______. 8．某班有50名学生，其中15人选修A课程，另外35人选修B课程.从班级中任选两名学生， 他们是选修不同课程的学生的概率是__________.（结果用分数表示） 1 9．直线y  x关于直线x 1对称的直线方程是__________. 2 10．在ABC中，若A120，AB=5，BC=7，则AC=__________.   11．函数 f(x) sinx2|sinx|,x 0,2 的图象与直线y  k 有且仅有两个不同的交点 ，则k的取值范围是__________. 2 12．有两个相同的直三棱柱，高为 ，底面三角形的 a 第1页 | 共8页三边长分别为3a,4a,5a(a0).用它们拼成一个三棱柱或四棱柱，在所有可能的情形中 ，全面积最小的是一个四棱柱，则a的取值范围是__________. 二、选择题（本大题满分16分）本大题共有4题，每题都给出代号为A、B、C、D的四个结 论，其中有且只有一个结论是正确的，必须把正确结论的代号写在题后的圆括号内， 选对得4分，不选、选错或者选出的代号超过一个（不论是否都写在圆括号内），一律 得零分. 1 13．若函数 f(x) ，则该函数在,上是 （ ） 2x 1 A．单调递减无最小值 B．单调递减有最小值 C．单调递增无最大值 D．单调递增有最大值 14．已知集合M x||x1|2,xR，P   x| 5 1,xZ  ，则M  P等于（ ）  x1  A．x|0 x3,xZ B．x|0 x3,xZ C．x|1 x0,xZ D．x|1 x0,xZ 15．条件甲：“a 1”是条件乙：“a  a”的 （ ） A．既不充分也不必要条件 B．充要条件 C．充分不必要条件 D．必要不充分条件 16．用n个不同的实数a ,a , ,a 可得到n!个不同的排列，每个排列为一行写成一个n! 1 2  n 行的数阵.对第i行a ,a , ,a ，记b  a 2a 3a  (1)nna ， i1 i2  in i i1 i2 i3  in i 1,2,3, ,n!.例如：用1，2，3可得数阵如图， 1 2 3  1 3 2 由于此数阵中每一列各数之和都是12，所以， 2 1 3 b b  b  12212312 24， 1 2  6 2 3 1 那么，在用1，2，3，4，5形成的数阵中， 3 1 2 3 2 1 b b  b 等于（ ） 1 2  120 A．－3600 B．1800 C．—1080 D．—720 三、解答题（本大题满分86分）本大题共有6题，解答下列各题必 须写出必要的步骤. 17．（本题满分12分）已知长方体ABCD A BC D 中，M、N 1 1 1 1 分别是BB 和BC的中点，AB=4，AD=2，B D与平面ABCD 1 1 第2页 | 共8页所成角的大小为60，求异面直线B D与MN所成角的大小.（结果用反三角函数值表 1 示） 3i 18．（本题满分12分）在复数范围内解方程| z|2 (z z)i  （i为虚数单位）. 2i 第3页 | 共8页19．（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分. 已知函数 f(x)  kxb的图象与x,y轴分别相交于点A、B，AB  2i2j（i, j分 别是与x,y轴正半轴同方向的单位向量），函数g(x)  x2 x6. （1）求k,b的值； g(x)1 （2）当x满足 f(x)  g(x)时，求函数 的最小值. f(x) 第4页 | 共8页20．（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分. 假设某市2004年新建住房面积400万平方米，其中有250万平方米是中低价房.预计在今 后的若干年内，该市每年新建住房面积平均比上一年增长8%.另外，每年新建住房中，中 低价房的面积均比上一年增加50万平方米.那么，到哪一年底， （1）该市历年所建中低价层的累计面积（以2004年为累计的第一年）将首次不少于47 50万平方米？ （2）当年建造的中低价房的面积占该年建造住房面积的比例首次大于85%？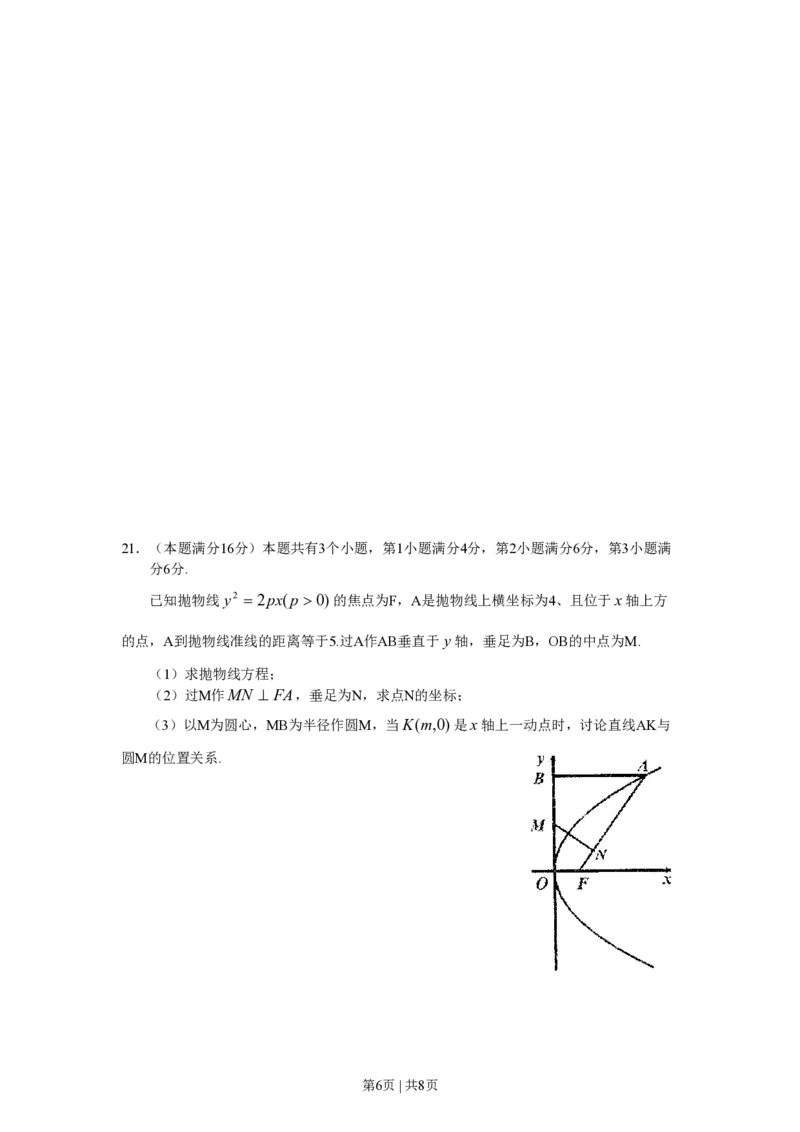 第5页 | 共8页21．（本题满分16分）本题共有3个小题，第1小题满分4分，第2小题满分6分，第3小题满 分6分. 已知抛物线y2  2px(p 0)的焦点为F，A是抛物线上横坐标为4、且位于x轴上方 的点，A到抛物线准线的距离等于5.过A作AB垂直于y轴，垂足为B，OB的中点为M. （1）求抛物线方程； （2）过M作MN  FA，垂足为N，求点N的坐标； （3）以M为圆心，MB为半径作圆M，当K(m,0)是x轴上一动点时，讨论直线AK与 圆M的位置关系. 第6页 | 共8页22．（本题满分18分）本题共有3个小题，第1小题满分4分，第2小题满分8分，第3小题满 分6分. 对定义域是D 、D 的函数y  f(x)、y  g(x)，规定：函数 f g f(x)g(x), 当xD 且xD f g  h(x)   f(x), 当xD 且xD . f g  g(x), 当xD 且xD  f g （1）若函数 f(x)  2x3，g(x)  x2，写出函数h(x)的解析式； （2）求问题（1）中函数h(x)的最大值；   （3）若g(x)  f(x)，其中是常数，且 0, ，请设计一个定义域为R的 函数y  f(x)，及一个的值，使得h(x) cos2x，并予以证明. 第7页 | 共8页第8页 | 共8页