广东省华南师范大学附属中学2024-2025学年高三上学期11月综合测试（二）数学PDF版含解析（可编辑）_2024-2025高三（6-6月题库）_2024年11月试卷

2025 届高三综合测试（二） 数 学 满分：150分 时间：120分钟 一、选择题：本题共8小题，每小题5分，共40分. 在每小题给出的四个选项中，只有一项是符合题目要 求的。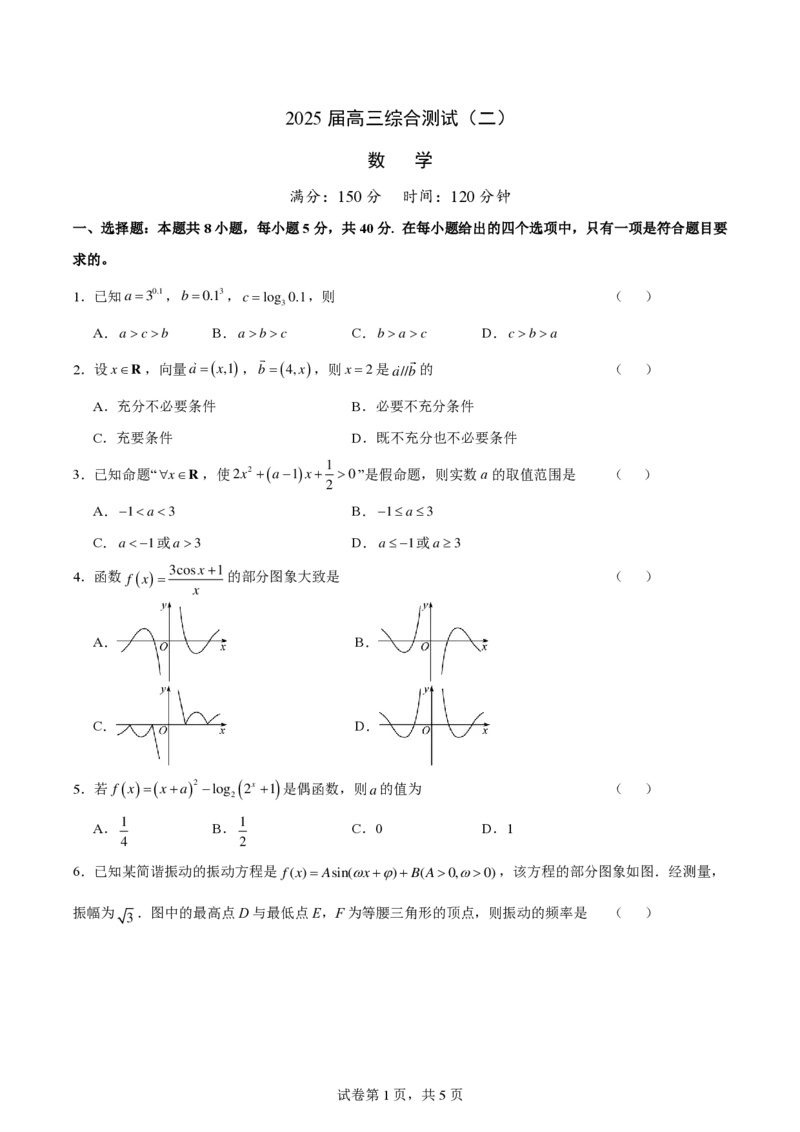 1．已知a=30.1， 试卷第1页，共5页 b = 0 .1 3 ， c = lo g 3 0 .1 ，则 （ ） A． a  c  b B． a  b  c C． b  a  c D． c  b  a 2．设 x  R ，向量 a = ( x ,1 ) ， b = ( 4 , x ) ，则 x = 2 是a//b的 （ ） A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 3．已知命题“  x  R ，使 2 x 2 + ( a − 1 ) x + 1 2  0 ”是假命题，则实数a的取值范围是 （ ） A． − 1  a  3 B． − 1  a  3 C． a  − 1 或 a  3 D． a  − 1 或 a  3 4．函数 f ( x ) = 3 c o s x x + 1 的部分图象大致是 （ ） A． B． C． D． 5．若 f ( x ) = ( x + a ) 2 − lo g 2 ( 2 x + 1 ) 是偶函数，则 a 的值为 （ ） 1 1 A． B． C．0 D．1 4 2 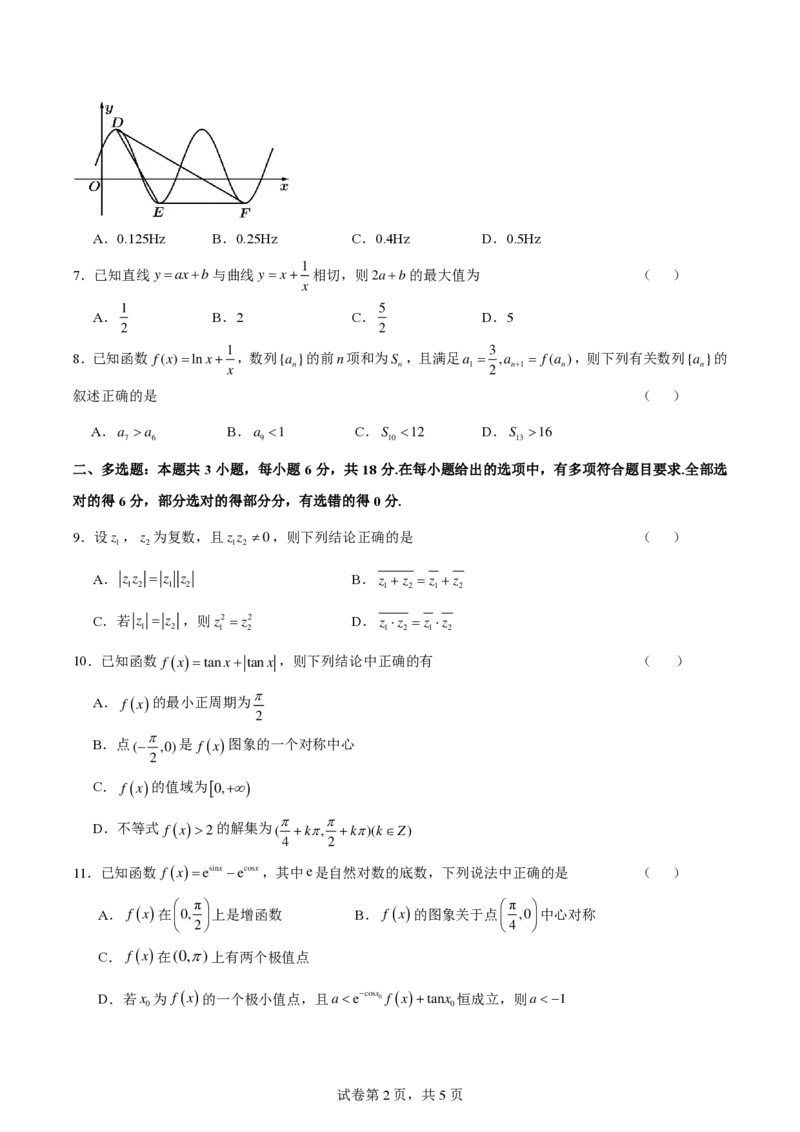6．已知某简谐振动的振动方程是 f(x)= Asin(x+)+B(A0,0)，该方程的部分图象如图．经测量， 振幅为 3 ．图中的最高点D与最低点E，F为等腰三角形的顶点，则振动的频率是 （ ） {{##{{QQQQAABBJLYYACEswgggiggwAkBAJaAAACAQgC4LAAQQ23AkCCggAoQQkkhoCCAgCJcYggEGxhQBCADMOIAAARBjSiBZFFAABFAIAA==}#}#}}A．0.125Hz B．0.25Hz C．0.4Hz D．0.5Hz 7．已知直线 试卷第2页，共5页 y = a x + b 与曲线 y = x + 1 x 相切，则 2 a + b 的最大值为 （ ） 1 5 A． B．2 C． D．5 2 2 1 3 8．已知函数 f(x)=lnx+ ，数列{a }的前n项和为S ，且满足a = ,a = f(a )，则下列有关数列 x n n 1 2 n+1 n { a n } 的 叙述正确的是 （ ） A．a a B． 7 6 a 9  1 C． S 1 0  1 2 D． S 1 3  1 6 二、多选题：本题共 3 小题，每小题 6 分，共 18 分.在每小题给出的选项中，有多项符合题目要求.全部选 对的得6分，部分选对的得部分分，有选错的得0分. 9．设z ， 1 z 2 为复数，且 z 1 z 2  0 ，则下列结论正确的是 （ ） A． z 1 z 2 = z 1 z 2 B． z 1 + z 2 = z 1 + z 2 C．若 z = z ，则z2 =z2 D． 1 2 1 2 z 1  z 2 = z 1  z 2 10．已知函数 f ( x ) = ta n x + ta n x ，则下列结论中正确的有 （ ） A． f ( x )  的最小正周期为 2 B．点 ( 2 , 0 )  − 是 f ( x ) 图象的一个对称中心 C． f ( x ) 的值域为  0 , )  + D．不等式 f ( x )  2   的解集为( +k, +k)(kZ) 4 2 11．已知函数 f (x)=esinx −ecosx，其中e是自然对数的底数，下列说法中正确的是 （ ） A． f ( x ) 在  0 , π 2  上是增函数 B． f ( x ) π  的图象关于点 ,0中心对称 4  C． f (x)在(0,)上有两个极值点 D．若x 为 f (x)的一个极小值点，且ae−cosx0 f (x)+tanx 恒成立，则a−1 0 0 {{##{{QQQQAABBJLYYACEswgggiggwAkBAJaAAACAQgC4LAAQQ23AkCCggAoQQkkhoCCAgCJcYggEGxhQBCADMOIAAARBjSiBZFFAABFAIAA==}#}#}}三、填空题：本题共3小题，每小题5分，共15分。 12．若集合 试卷第3页，共5页 A = { x | x 2 + a x + b = 0 } ， B = { x | x 2 + c x + 6 = 0 } ， A B =  2  ， A B = B ，则 a + b + c = . 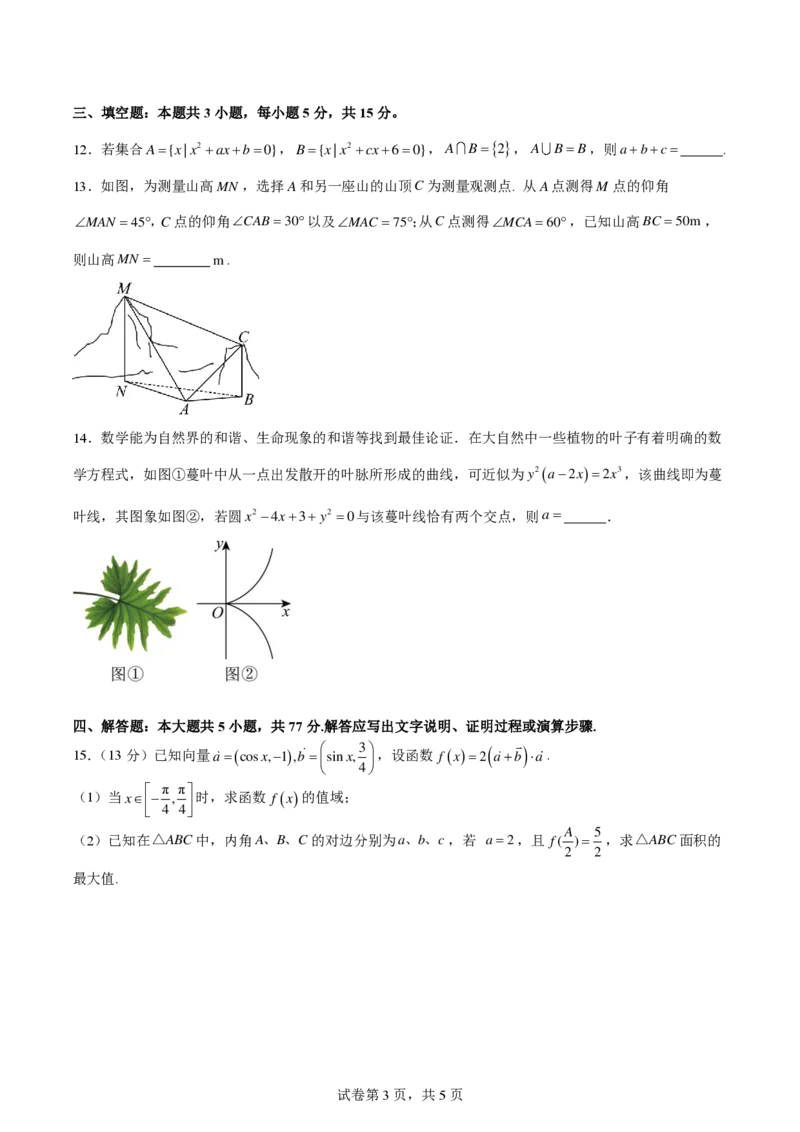13．如图，为测量山高 M N ，选择A和另一座山的山顶 C 为测量观测点. 从 A 点测得 M 点的仰角  M A N = 4 5  ， C 点的仰角  C A B = 3 0  以及  M A C = 7 5  ； 从 C 点测得  M C A = 6 0  ，已知山高 B C = 5 0 m ， 则山高 M N = m . 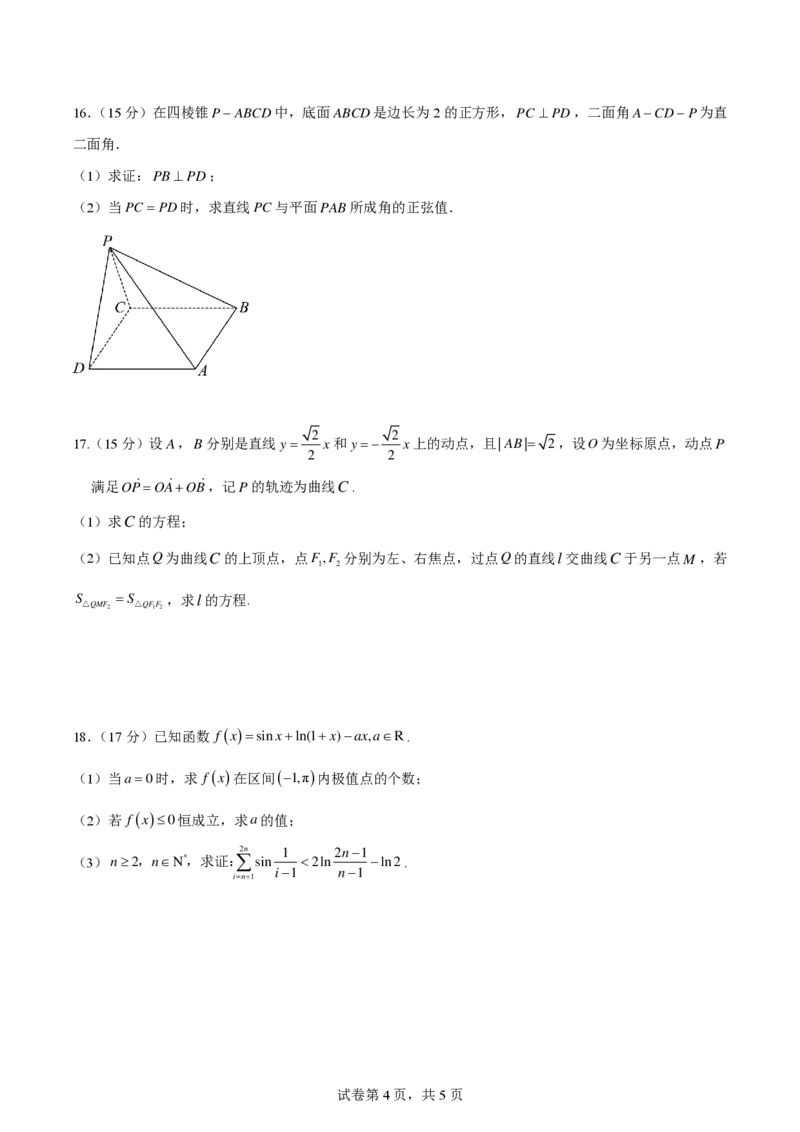14．数学能为自然界的和谐、生命现象的和谐等找到最佳论证．在大自然中一些植物的叶子有着明确的数 学方程式，如图①蔓叶中从一点出发散开的叶脉所形成的曲线，可近似为 y 2 ( a − 2 x ) = 2 x 3 ，该曲线即为蔓 叶线，其图象如图②，若圆x2 −4x+3+ y2 =0与该蔓叶线恰有两个交点，则 a = ． 四、解答题：本大题共5小题，共77分.解答应写出文字说明、证明过程或演算步骤. 15．（13分）已知向量a=(cosx,−1),b =  sinx, 3  ，设函数 f (x)=2 ( a+b ) a.  4  π π （1）当x − , 时，求函数    4 4 f ( x ) 的值域； （2）已知在△ABC中，内角A、B、C的对边分别为 a 、 b 、 c A 5 ，若 a=2，且 f( )= ，求△ABC面积的 2 2 最大值. {{##{{QQQQAABBJLYYACEswgggiggwAkBAJaAAACAQgC4LAAQQ23AkCCggAoQQkkhoCCAgCJcYggEGxhQBCADMOIAAARBjSiBZFFAABFAIAA==}#}#}}16．（15分）在四棱锥 试卷第4页，共5页 P − A B C D 中，底面 A B C D 是边长为2的正方形， P C ⊥ P D ，二面角 A − C D − P 为直 二面角． （1）求证：PB⊥PD； （2）当 P C = P D 时，求直线 P C 与平面 P A B 所成角的正弦值． 17.（15分）设 A ， B 分别是直线 y = 2 2 x 和 y = − 2 2 x 上的动点，且 | A B |= 2 ，设 O 为坐标原点，动点 P 满足 O P = O A + O B ，记P的轨迹为曲线 C . （1）求C的方程； （2）已知点 Q 为曲线 C 的上顶点，点 F 1 , F 2 分别为左、右焦点，过点 Q 的直线l交曲线 C 于另一点M ，若 S △ Q M F 2 = S △ Q F F1 2 ，求 l 的方程. 18．（17分）已知函数 f ( x ) = s in x + ln (1 + x ) − a x , a  R . （1）当a=0时，求 f ( x ) 在区间 ( − 1 , π ) 内极值点的个数； （2）若 f (x)0恒成立，求a的值； （3） n  2 ， n  N *， 求 证 ： 2 n i= n + 1 s in i 1 − 1  2 ln 2 n n − − 1 1 − ln 2 . {{##{{QQQQAABBJLYYACEswgggiggwAkBAJaAAACAQgC4LAAQQ23AkCCggAoQQkkhoCCAgCJcYggEGxhQBCADMOIAAARBjSiBZFFAABFAIAA==}#}#}}19. （17分）进位制是人们为了计数和运算方便而约定的记数系统，约定满二进一，就是二进制；满十进一， 就是十进制；满十六进一，就是十六进制等等。一般地，若 试卷第5页，共5页 k 是一个大于1的整数，那么以 k 为基数的 k 进 制数可以表示为一串数字符号连写在一起的形式a a ...aa (a ,a ,...,a,a 0,1,2,...,k−1,a 0)， n n−1 1 0(k) n n−1 1 0 n k 进 制 的 数 也 可 以 表 示 成 不 同 位 上 数 字 符 号 与 基 数 的 幂 的 乘 积 之 和 的 形 式 ， 如 a n a n − 1 ...a 1 a 0 (k ) = a n k n + a n − 1 k n − 1 + ... + a 1 k + a 0 . 例如十进制数 2 5 = 2  3 2 + 2  3 + 1 ，所以 2 5 在三进制下可写为 221 . (3) （1）设正整数 m 在三进制下的各位数字之和为 S ( m ) （i）将满足 S ( m ) = 3 的数从小到大排成一列，直接写出该列数的前四个数； （ii）在1至2025中任选一个正整数 m ，求 S ( m ) 为3的倍数的概率. （2）已知正项数列  a n  的前 n 项和为 S ， n a 1 = a 2 ( a  N  , a  3 1 ) ，且 S n S n − 1 + ( S n − 1 + 2 a ) a n = a 2 ，记 M =  a 1 + 1 2  +  a 2 + 1 2  + ... +  a n + 1 2  + ... （其中  x  表示不大于 x 的最大整数），求M 的值.（用 a 表示） {{##{{QQQQAABBJLYYACEswgggiggwAkBAJaAAACAQgC4LAAQQ23AkCCggAoQQkkhoCCAgCJcYggEGxhQBCADMOIAAARBjSiBZFFAABFAIAA==}#}#}}2025 届高三综合测试（二）数 学 参考答案 1．B 2．A 3．D 4．A 5．A 6．B 7．C 8．C 7.【详解】设切点横坐标为 答案第1页，共11页 m ( m  0 ) ，求导： y = x + 1 x 得 y ' = 1 − 1 x 2 ， 由题意可得  a a = m 1 + − b m = 1 2 m + 1 m  1 a=1−   m2 解得： ，  2 b=  m 2 2  1 1 2 5 所以2a+b=− + +2=−2 −  + ， m2 m m 2 2 所以 m = 2 时，2a+b的最大值为 5 2 . 故选:C 8.【详解】由 f ( x ) = ln x + 1 x ，求导得 f '( x ) = x − 2 x 1  0 , ( x  1 ) ，  f ( x ) 在 (1 , +  ) 单调递增，故 f ( x )  f (1 ) = 1 。 a 1 = 3 2  1 ，  a 2 = f ( a 1 )  f ( 1 ) = 1 ，迭代下去，可得 a n  1 。故B错误； 3 3 2 1 2 7 由a = ，a = f (a )=ln +  + = ，故 1 2 2 1 2 3 2 3 6 a 2  a 1 迭代下去，可得 1  a n  a n − 1    a 1 = 3 2 ，数列{a }单调递减。 n 故A错误； S 1 0  a 1 + 9 a 2  3 2 + 7 6  9 = 1 2 ，故C正确 3 7 S a +12a  + 12=15.5，故D错误． 13 1 2 2 6 故选： C ． 9．ABD 【详解】设 z 1 = a + b i ， z 2 = c + d i (a,b,c,dR)， 对于选项A，因为z z =(a+bi)(c+di)=(ac−bd)+(ad +bc)i， 1 2 所以 z 1 z 2 = ( a c − b d ) 2 + ( a d + b c ) 2 = a 2 c 2 + b 2 d 2 + a 2 d 2 + b 2 c 2 ， 且 z z = a2 +b2 c2 +d2 = a2c2 +b2d2 +a2d2 +b2c2 ，所以 1 2 z 1 z 2 = z 1 z 2 ，故A正确； 对于选项B，因为z +z =(a+c)+(b+d)i，z =a−bi，z =c−di， 1 2 1 2 {{##{{QQQQAABBJLYYACEswgggiggwAkBAJaAAACAQgC4LAAQQ23AkCCggAoQQkkhoCCAgCJcYggEGxhQBCADMOIAAARBjSiBZFFAABFAIAA==}#}#}}则 答案第2页，共11页 z 1 + z 2 = ( a + c ) − ( b + d ) i ， z 1 + z 2 = ( a + c ) − ( b + d ) i ， 所以z +z =z +z ，故B正确； 1 2 1 2 对于选项C，若 z 1 = z 2 ，例如 z 1 = 1 + i ， z 2 = 1 − i ，满足 z 1 = z 2 = 2 ， 但z2 =(1+i)2 =2i，z2 =(1−i)2 =−2i，即z2  z2，故C错误； 1 2 1 2 对于选项D，因为z z =(a+bi)(c+di)=(ac−bd)+(ad+bc)i， 1 2 所以 z 1  z 2 = ( a c − b d ) − ( a d + b c ) i ， z 1  z 2 = ( a − b i ) ( c − d i ) = ( a c − b d ) − ( a d + b c ) i ， 所以z z =z z ，故D正确. 1 2 1 2 故选：ABD. 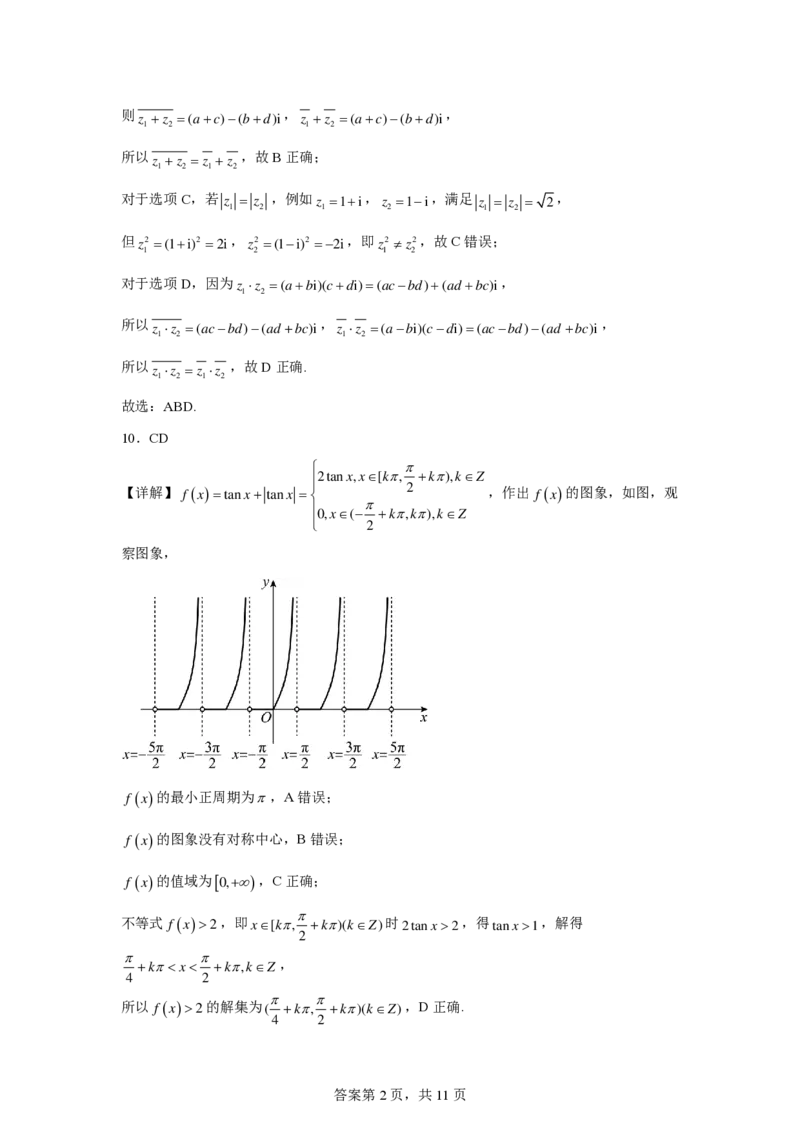10．CD 【详解】 f ( x ) ta n x ta n x 2 0 ta , x n x , ( x 2 [ k k , 2 , k k ) , k ) , k Z Z       = + =   −  + +   ，作出 f ( x ) 的图象，如图，观 察图象， f ( x ) 的最小正周期为，A错误； f (x)的图象没有对称中心，B错误； f ( x ) 的值域为0,+)，C正确；  不等式 f (x)2，即x[k, +k)(kZ)时2tanx2，得tanx1，解得 2   +kx +k,kZ ， 4 2   所以 f (x)2的解集为( +k, +k)(kZ)，D正确. 4 2 {{##{{QQQQAABBJLYYACEswgggiggwAkBAJaAAACAQgC4LAAQQ23AkCCggAoQQkkhoCCAgCJcYggEGxhQBCADMOIAAARBjSiBZFFAABFAIAA==}#}#}}故选：CD 11．ABD 【详解】由题设， 答案第3页，共11页 f ( x ) = e sin x c o s x + e co s x s in x ，  π A：在 0,  上 f(x)0，故  2 f ( x )  π 在 0,  是增函数，A正确；  2 B：g(x)= f(x+ π )=e sin(x+ π 4 ) −e cos(x+ π 4 )， 4 则 = g ( − co s( e π2 x + ) x = π − 4 sin (− x + e ) sin ( − e π4 π2 ) + − x − co s(− e π ) = e 4 x + co π ) 4 s(x = π + 4 e ) − − sin e π (x − ) 4 sin (x + − π ) 4 e = co s(x − g π − ) 4 ( x ) π ，即 f(x+ )是奇函数， 4 图象关于点  π 4 , 0  中心对称，故B正确； C：若在 ( 0 , π ) 上有极值点，令 f ( x ) = 0 则有 c s o s in x x = − e co s x − sin x  0 ， 而 s in x  0 ，此时cosx0，所以极值点在  π 2 , π  上， 令h(x)= f(x)，有 h ( x ) = e sin x ( c o s 2 x − s in x ) + e co s x ( c o s x − s in 2 x ) ， π 3π ∴在  ,  上， 2 4  c o s 2 x − s in x  0 ， c o s x − s in 2 x  0 ，即 h ( x )  0 ， f ( x ) 单调递减； 又 f ( π 2 ) = 1 ， f ( 3 π 4 ) = 2 2 ( e − 22 − e 22 )  0 ，显然存在 f(x)=0， 在  3 π 4 , π  上， s in x  c o s x 且 c o s x  0 ， s in x  0 ，故sinx−cosx， ∴ 0ecosx 1esinx，则 c o s x e sin x  s in x e co s x ， 即 f(x)=esinxcosx+ecosxsinx0，∴ f ( x ) 不存在零点； 综上， f(x)在 ( 0 , π ) 上只有一个极值点，故C错误； D：易知 f ( x ) 为周期函数，T =2π是其一个周期， 由C知：  x 1   π 2 , 3 π 4  ，使得 f(x )=0， 1 π  ∵ f(x)=esinx −ecosx在  ,x  上 2 1  f ( x )  0 ，即 f ( x ) 递增，  3π 在 x,  上 f(x)0即 f(x)递减，即 f (x )为 f(x)在  1 4  1 ( 0 , π ) 上的极大值，也是最大值， 又由B项的结论：x (−π,0)使得 f (x )为 f(x)在(−π,0)上的极小值，也是最小值， 2 2 {{##{{QQQQAABBJLYYACEswgggiggwAkBAJaAAACAQgC4LAAQQ23AkCCggAoQQkkhoCCAgCJcYggEGxhQBCADMOIAAARBjSiBZFFAABFAIAA==}#}#}}则x =x +2kπ(kZ)，且 0 2 答案第4页，共11页 x 1 + x 2 = π 2 ， f (x )+ f (x )=0， 1 2 不妨令 k = 0 π ，则x =x = −x ， 0 2 2 1 令 g ( x ) = e sin x e − co s e x0 co s x + ta n x 0 ，则 g ( x ) m in = f ( x co e ) m s x0 in + ta n x 0 π  ecosx1 −esinx1 1 即ag(x) =g(x )=g −x = + ， min 2 2 1  esinx1 tanx 1 而结合C知有 − e co s x1 − sin x1 = ta 1 n x 1 ，∴ g ( x ) m ax = − 1 ，故 a  − 1 ，正确. 故选：ABD 12．【答案】-5 13．【答案】50 3 14.【答案】 6 + 3 3 【详解】 方法一：根据蔓叶线和圆的对称性，圆 ( x − 2 ) 2 + y 2 = 1 与该蔓叶线恰有两个交点， 即当y0时，圆和蔓叶线的上半部分只有一个交点， 即方程 ( 4 x − x 2 − 3 )  a 2 − x  = x 3 (1  x  3 ) 有一个实数根， 即方程 a 2 = 4 4 x x − 2 − x 2 3 x − 3 (1  x  3 ) 有一个实数根， 令 f ( x ) = 4 4 x x − 2 − x 2 3 x − 3 (1  x  3 ) ，则 f  ( x ) = 1 ( 3 4 x x 2 − − 2 4 2 x x − + 3 ) 9 2 ， 令 f  ( x ) = 0 ，则 x = 1 2 + 1 3 3 3 或 1 2 − 1 3 3 3 （舍）， 所以 f (x)在区间  1 , 1 2 + 1 3 3 3  12+3 3  内单调递减，在区间 ,3内单调递增，   13   12+3 3 6+3 3 所以 f(x) = f  = ， min  13  2   x → 1 + , f ( x ) → +  , x → 3 − , f ( x ) → +  , 故当a=6+3 3时，圆x2 −4x+3+ y2 =0与该蔓叶线恰有两个交点． 方法二：根据蔓叶线和圆的对称性，圆(x−2)2 + y2 =1与该蔓叶线恰有两个交点， 即当y0时，圆和蔓叶线的上半部分只有一个交点，此时两个曲线相切,故 {{##{{QQQQAABBJLYYACEswgggiggwAkBAJaAAACAQgC4LAAQQ23AkCCggAoQQkkhoCCAgCJcYggEGxhQBCADMOIAAARBjSiBZFFAABFAIAA==}#}#}}答案第5页，共11页 a 2 = 4 4 x x − 2 − x 2 3 x − 3 (1  x  3 ) ，此时(8+a)x2 −(6+4a)x+3a=0，  = 0 ， 故(6+4a)2 −12a(a+8)=0，解得 a = 6  3 3 ，当 a = 6 − 3 3 时，x1不符合题意， 当a=6−3 3时， x = 1 2 + 1 3 3 3 符合题意. 故答案为： 6 + 3 3 . 15．【详解】（1） a + b =  c o s x + s in x , − 1 4  ，  1 1 f(x)=2(a+b)a=2cosx+sinx,− (cosx,−1)=2cos2x+2sinxcosx+ ………1分  4 2 = s in 2 x + c o s 2 x + 3 2 = 2 s in  2 x + π 4  + 3 2 ， ………3分   π π π  π 3π 当x − , 时，2x+  − , ， ………4分      4 4 4  4 4    π  2  sin2x+ − ,1 ………5分  4  2   2 s in  2 x + π 4  + 3 2   1 2 , 2 + 3 2  ， 所以函数 f ( x ) 的值域为  1 2 , 2 + 3 2  ………6分 （2）由（1）可知 f ( x ) = 2 s in  2 x + π 4  + 3 2 ， 又 f ( A 2 ) = 5 2 ，所以 s in  A + π 4  = 2 2 ， 因为 A  ( 0 , π ) ，所以 A + π 4   π 4 , 5 π 4  π ，故A= ， ………8分 2 因为a=2，由 a 2 = b 2 + c 2 可知， 4 = b 2 + c 2 ， ………9分 由基本不等式得 4 = b 2 + c 2  2 b c ， 解得 b c  2 ，当且仅当 b = c = 2 时，等号成立， ………11分 故三角形面积 1 2 b c s in A  1 2  2  1 = 1 ， 即 ABC 面积最大值为1. ………13分 16．【详解】：（1）证明：由于底面 A B C D 是边长为2的正方形，则 B C ⊥ C D ， 由于二面角 A − C D − P 为直二面角， C D = 平 面 A C D 平 面 P C D ,则 B C ⊥ 平面 P C D ， 2分 {{##{{QQQQAABBJLYYACEswgggiggwAkBAJaAAACAQgC4LAAQQ23AkCCggAoQQkkhoCCAgCJcYggEGxhQBCADMOIAAARBjSiBZFFAABFAIAA==}#}#}}由于PD平面 答案第6页，共11页 P C D ，则 P D ⊥ B C ，又 P C ⊥ P D ，PC BC=C， P C 、 B C  平面 P B C ， 则PD⊥平面 P B C ，       5分 由于PB平面PBC ，则 P B ⊥ P D ．6分 （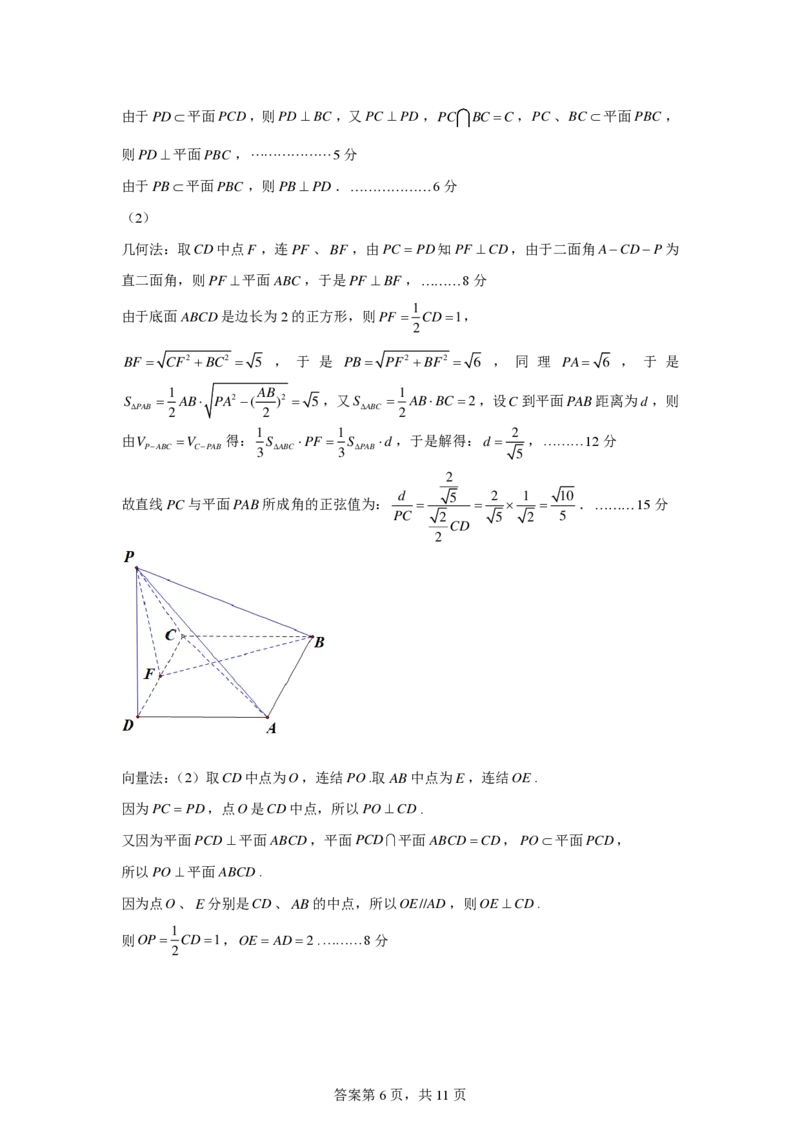2） 几何法：取 C D 中点F ，连PF、BF，由 P C = P D 知 P F ⊥ C D ，由于二面角 A − C D − P 为 直二面角，则 P F ⊥ 平面 A B C ，于是 P F ⊥ B F ，    8分 由于底面 A B C D 是边长为2的正方形，则 P F = 1 2 C D = 1 ， B F = C F 2 + B C 2 = 5 ， 于 是 PB= PF2 +BF2 = 6 ， 同 理 PA= 6 ， 于 是 S  P A B = 1 2 A B  P A 2 − ( A B 2 ) 2 = 5 ，又 S  A B C = 1 2 A B  B C = 2 ，设 C 到平面 P A B 距离为d ，则 由 V P − A B C = V C − P A B 得： 1 3 S  A B C  P F = 1 3 S  P A B  d 2 ，于是解得：d = ，12分 5 故直线 P C 与平面 P A B 所成角的正弦值为： P d C = 2 2 2 5 C D = 2 5  1 2 = 1 5 0 ．    15分 向量法：（2）取 C D 中点为 O ，连结 P O .取 A B 中点为 E ，连结 O E . 因为 P C = P D ，点 O 是 C D 中点，所以 P O ⊥ C D . 又因为平面PCD⊥平面ABCD，平面PCD 平面ABCD=CD，PO平面 P C D ， 所以PO⊥平面ABCD. 因为点 O 、 E 分别是 C D 、AB的中点，所以OE//AD，则 O E ⊥ C D . 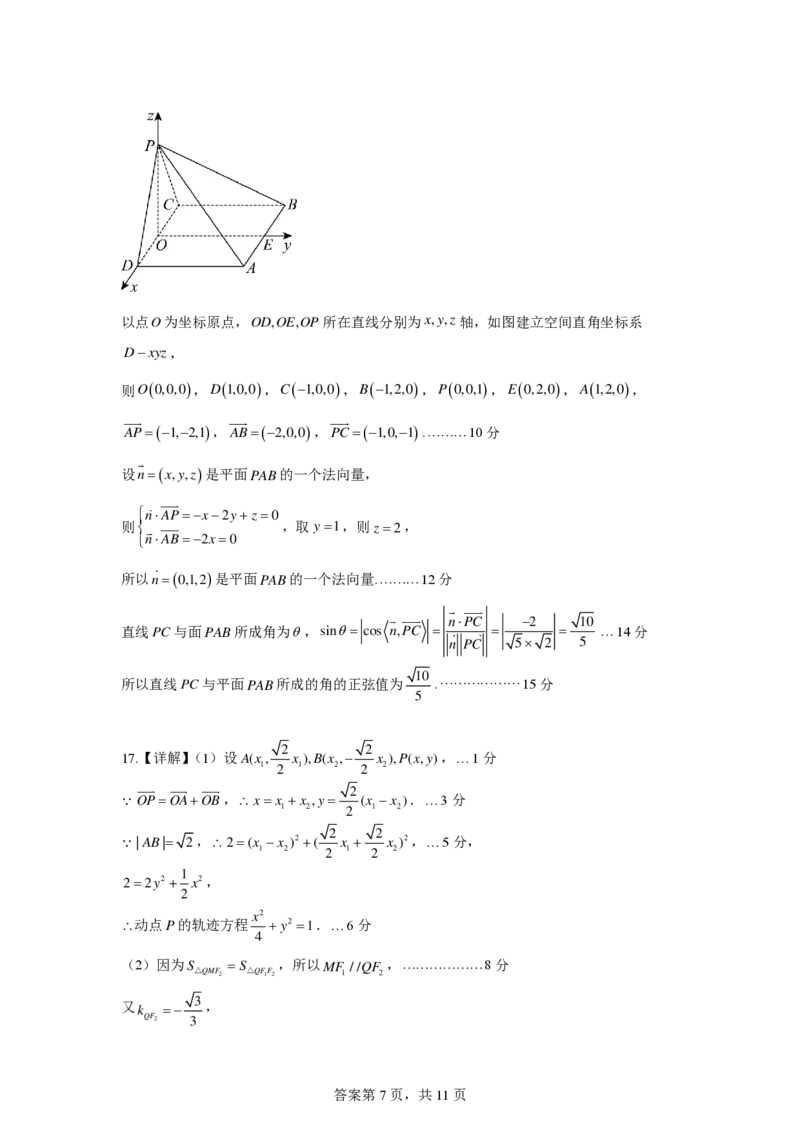1 则OP= CD=1，OE= AD=2.8分 2 {{##{{QQQQAABBJLYYACEswgggiggwAkBAJaAAACAQgC4LAAQQ23AkCCggAoQQkkhoCCAgCJcYggEGxhQBCADMOIAAARBjSiBZFFAABFAIAA==}#}#}}以点 答案第7页，共11页 O 为坐标原点，OD,OE,OP所在直线分别为 x , y , z 轴，如图建立空间直角坐标系 D − x y z ， 则 O ( 0 , 0 , 0 ) ， D ( 1 , 0 , 0 ) ，C(−1,0,0)， B ( − 1 , 2 , 0 ) ， P ( 0 , 0 ,1 ) ， E ( 0 , 2 , 0 ) ， A ( 1 , 2 , 0 ) ， A P = ( − 1 , − 2 ,1 ) ， A B = ( − 2 , 0 , 0 ) ， P C = ( − 1 , 0 , − 1 ) .10分 设n=(x,y,z)是平面 P A B 的一个法向量， 则  n n   A A P B = = − − x 2 − x 2 = y 0 + z = 0 ，取 y = 1 ，则 z = 2 ， 所以 n = ( 0 ,1 , 2 ) 是平面 P A B 的一个法向量.    12分 直线 P C 与面 P A B 所成角为， s in c o s n , P C n n P P C C 5 2 2 1 5 0  = =  = −  = 14分 所以直线 P C 与平面 P A B 所成的角的正弦值为 1 5 0 . 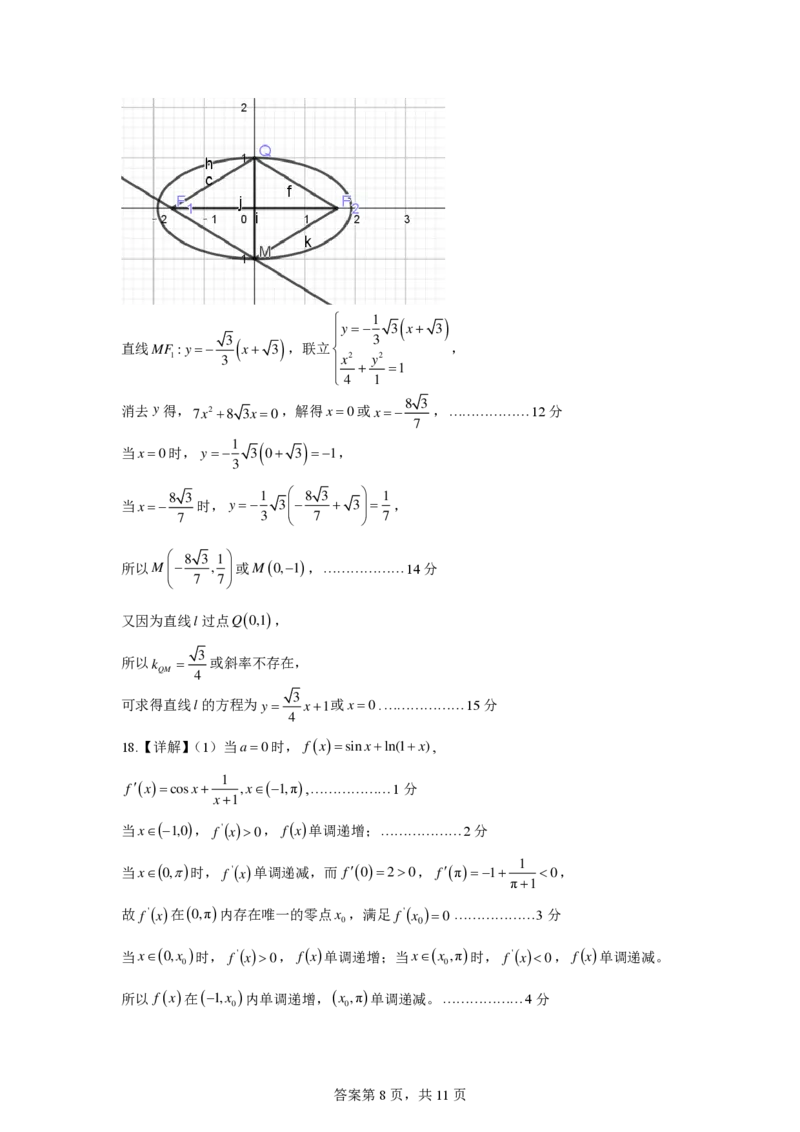      15分 2 2 17.【详解】（1）设A(x, x ),B(x ,− x ),P(x,y)，1分 1 2 1 2 2 2 O P = O A + O B 2 ，x=x +x ,y= (x −x )． 1 2 2 1 2  3分 |AB|= 2，  2 2 2=(x −x )2 +( x + x )2， 1 2 2 1 2 2  5分， 1 2=2y2 + x2， 2 x2 动点P的轨迹方程 + y2 =1． 4  6分 （2）因为S =S ，所以MF //QF ，8分 △QMF2 △QF1F2 1 2 3 又k =− ， QF2 3 {{##{{QQQQAABBJLYYACEswgggiggwAkBAJaAAACAQgC4LAAQQ23AkCCggAoQQkkhoCCAgCJcYggEGxhQBCADMOIAAARBjSiBZFFAABFAIAA==}#}#}}直线 答案第8页，共11页 M F 1 : y = − 3 3 ( x + 3 ) ，联立  y x 4 = 2 + − 1 3 y 1 2 3 = ( 1 x + 3 ) ， 消去 y 得，7x2 +8 3x=0，解得 x = 0 或 x = − 8 7 3 ，12分 当 x = 0 时， y = − 1 3 3 ( 0 + 3 ) = − 1 ， 当 x = − 8 7 3 时， y = − 1 3 3  − 8 7 3 + 3  = 1 7 ， 所以 M  − 8 7 3 , 1 7  或M(0,−1)，14分 又因为直线 l 过点Q(0,1)， 所以 k Q M = 4 3 或斜率不存在， 可求得直线 l 的方程为 y = 4 3 x + 1 或 x = 0 .       15分 18.【详解】（1）当 a = 0 时， f ( x ) = s in x + ln (1 + x ) , f  ( x ) = c o s x + x 1 + 1 , x  ( − 1 , π ) ,       1分 当x(−1,0)， f (' x )  0 ， f ( x ) 单调递增；2分 当x(0,)时， f'(x)单调递减，而 f(0)=20， f  ( π ) = − 1 + π 1 + 1  0 ， 故 f'(x)在(0,π)内存在唯一的零点 x 0 ，满足 f (' x 0 ) = 0       3分 当x(0,x )时， 0 f (' x )  0 ， f ( x ) 单调递增；当x(x ,π)时， 0 f (' x )  0 ， f ( x ) 单调递减。 所以 f (x)在(−1,x )内单调递增，(x ,π)单调递减。4分 0 0 {{##{{QQQQAABBJLYYACEswgggiggwAkBAJaAAACAQgC4LAAQQ23AkCCggAoQQkkhoCCAgCJcYggEGxhQBCADMOIAAARBjSiBZFFAABFAIAA==}#}#}}故 f (x)在(−1,π)存在1个极大值点，无极小值点。5分 （2） f(x)0在 答案第9页，共11页 x  ( − 1 ,+  ) 恒成立，且 f ( 0 ) = 0 。  0是 f ( x ) 的极大值点，故 f'(0)=0；又 f  ( x ) = c o s x + x 1 + 1 − a , ，  a = 2    6分 当a=2，此时 f  ( x ) = c o s x + x 1 + 1 − 2 , 显然当𝑥 ∈(0,+∞)时， f  ( x )  1 + 1 − 2 = 0 ， 故 f (x)在(0,+∞)上为减函数；此时 f ( x )  0 。7分 当 x  ( − 1 , 0 ) 时，令 g ( x ) = f (' x ) ， 1 g'(x)=−sinx− −sinx−10， (x+1)2 故 g ( x ) 在 ( − 1 , 0 ) 上单调递减，  g ( x )  g ( 0 ) = 0 。8分  f ( x ) 在 ( − 1 , 0 ) 上单调递增。故  x  ( − 1 , 0 ) ， f ( x )  f ( 0 ) = 0 ， 从而 f (x)0在 x  ( − 1 ,+  ) 恒成立，故a=2。       9分 （3）由（2）可知， s in x  2 x − ln ( x + 1 ) ，当且仅当 x = 0 时取等号， 2n 1 2n 1 2n  1  所以 sin 2 −  ln1+  ， i−1 i−1  i−1 i=n+1 i=n+1 i=n+1       11分 2 n i= n + 1 ln  1 + i 1 − 1  = 2 n i= n + 1 ln  i i − 1  = ln n + n 1 + ln n n + + 2 1 + + ln 2 2 n n − 1 = ln 2 ， 因为 ln 2 n n − − 1 1 = ln  2 2 n n − − 1 2  2 2 n n − − 2 3 n n − 1  = ln 2 2 n n − − 1 2 + ln 2 2 n n − − 2 3 + + ln n n − 1 = 2 n i= n + 1 ln  n n − − 1 2  ， 1 i−1 所以即证 ln  i−1 i−2       13分 令 x i i 1 2 1 i 1 2 ( 1 , )  = − − = + −  + ，则 i 1 − 1 = 1 − 1 x ，14分 1 所以即证：1− lnx，𝑥 ∈(1,+∞)， x       15分 令 m ( x ) = 1 − 1 x − ln x ，则 m  ( x ) = 1 x 2 − 1 x = 1 − x 2 x ， 所以𝑥 ∈(1,+∞)时， m  ( x )  0 ，m(x)单调递减， 1 所以m(x)m(1)=0，即1− lnx，𝑥 ∈(1,+∞)，16分 x {{##{{QQQQAABBJLYYACEswgggiggwAkBAJaAAACAQgC4LAAQQ23AkCCggAoQQkkhoCCAgCJcYggEGxhQBCADMOIAAARBjSiBZFFAABFAIAA==}#}#}}2n 1 2n−1 综上， sin 2ln −ln2， i−1 n−1 i=n+1 答案第10页，共11页 n  2 ， n  N  17分 19【详解】 （1）（i）5,7,11,13 ………2分 （ii）设 m = 3 n a n + 3 n − 1 a n − 1 + ... + 3 a 1 + a 0 若 m 为3的倍数，则 a 0 为3的倍数，即 a 0 = 0 ， 所以m=a a ...a 0 ， n n−1 1 (3) m + 1 = a n a n − 1 ...a 11 (3 ) ， m + 2 = a n a n − 1 ...a 1 2 (3 ) S ( m ) = a n + a n − 1 + ... + a 1 S ( m + 1 ) = a n + a n − 1 + ... + a 1 + 1 S ( m + 2 ) = a n + a n − 1 + ... + a 1 + 2 所以当 m 为3的倍数时， S ( m ) , S ( m + 1 ) , S ( m + 2 ) 中恰有一个是3的倍数 ………5分 S ( 1 ) = 1 ， S ( 2 ) = 2 ， 2 0 2 5 = 2 2 1 0 0 0 0 (3 ) ， S ( 2 0 2 5 ) = 5 所以S(1),S(2),S(2025)都不是3的倍数 ………7分 而 S ( 3 ) , S ( 4 ) , ..., S ( 2 0 2 4 ) 这2022个数中，有 2 0 2 3 2 = 6 7 4 个是3的倍数 所以S(m)为3的倍数的概率为 6 7 4 2 0 2 5 . ………8分 （3）因为S S +(S +2a)a =a2， n n−1 n−1 n S n − 1 = S n − a n ( n  2 ) 所以S (S −a )+(S −a +2a)a =a2， n n n n n n S 2n = ( a n − a ) 2 ………9分 S =a −a或S =a−a n n n n 因为a 为正项数列，所以S a a −a，所以 n n n n S n = a − a n ( n  2 ) ………10分 因为 S 1 = a 1 = a 2 ，所以S =a−a ( nN) n n S =a−a (n2) n−1 n−1 两式作差得 a n = 1 2 a n − 1 a 1 所以a 是以 为首项， 为公比的等比数列，可得 n 2 2 a n = a 2 n ………12分 因为a31，所以设a=24x +23x +22x +2x +x (x ,x,x ,x ,x 0,1) ………13分 4 3 2 1 0 0 1 2 3 4 {{##{{QQQQAABBJLYYACEswgggiggwAkBAJaAAACAQgC4LAAQQ23AkCCggAoQQkkhoCCAgCJcYggEGxhQBCADMOIAAARBjSiBZFFAABFAIAA==}#}#}}则 答案第11页，共11页  a 1 + 1 2  =  2 4 x 4 + 2 3 x 3 + 2 2 2 x 2 + 2 x 1 + x 0 + 1  = 2 3 x 4 + 2 2 x 3 + 2 x 2 + x 1 +  x 0 + 2 1  ， 当 x 0 = 0 时，  x 0 + 2 1  = 0 ，当 x 0 = 1 时，  x 0 + 2 1  = 1 x +1  1 所以 0 =x ，即 a + =23x +22x +2x +x +x ………14分   2   0   1 2   4 3 2 1 0  x 2 + 1 2  =  2 4 x 4 + 2 3 x 3 + 2 2 x 2 22 + 2 ( x 1 + 1 ) + x 0  = 2 2 x 4 + 2 x 3 + x 2 +  2 ( x 1 + 2 1 2 ) + x 0  当 x 1 = 0 2(x +1)+x  2+x  时，  1 0 =  0  =0，当  22   4  x 1 = 1 2(x +1)+x  4+x  时，  1 0 =  0  =1  22   4  所以  2 ( x 1 + 2 1 2 ) + x 0  = x 1 ，即  a 2 + 1 2  = 2 2 x 4 + 2 x 3 + x 2 + x 1 ………15分 同理可得  a 3 + 1 2  = 2 x 4 + x 3 + x 2  a 4 + 1 2  = x 4 + x 3  a 5 + 1 2  = x 4 当 n  6 1 a 1 31 1 时，a + = +  + 1，所以 n 2 2n 2 64 2  a n + 1 2  = 0 ………16分 所以  1  1  1 M = a + + a + +...+ a +   1 2     2 2     5 2   = ( 23 +22 +2+1+1 ) x + ( 22 +2+1+1 ) x +(2+1+1)x +(1+1)x +x ………17分 4 3 2 1 0 =24x +23x +22x +2x +x 4 3 2 1 0 =a {{##{{QQQQAABBJLYYACEswgggiggwAkBAJaAAACAQgC4LAAQQ23AkCCggAoQQkkhoCCAgCJcYggEGxhQBCADMOIAAARBjSiBZFFAABFAIAA==}#}#}}