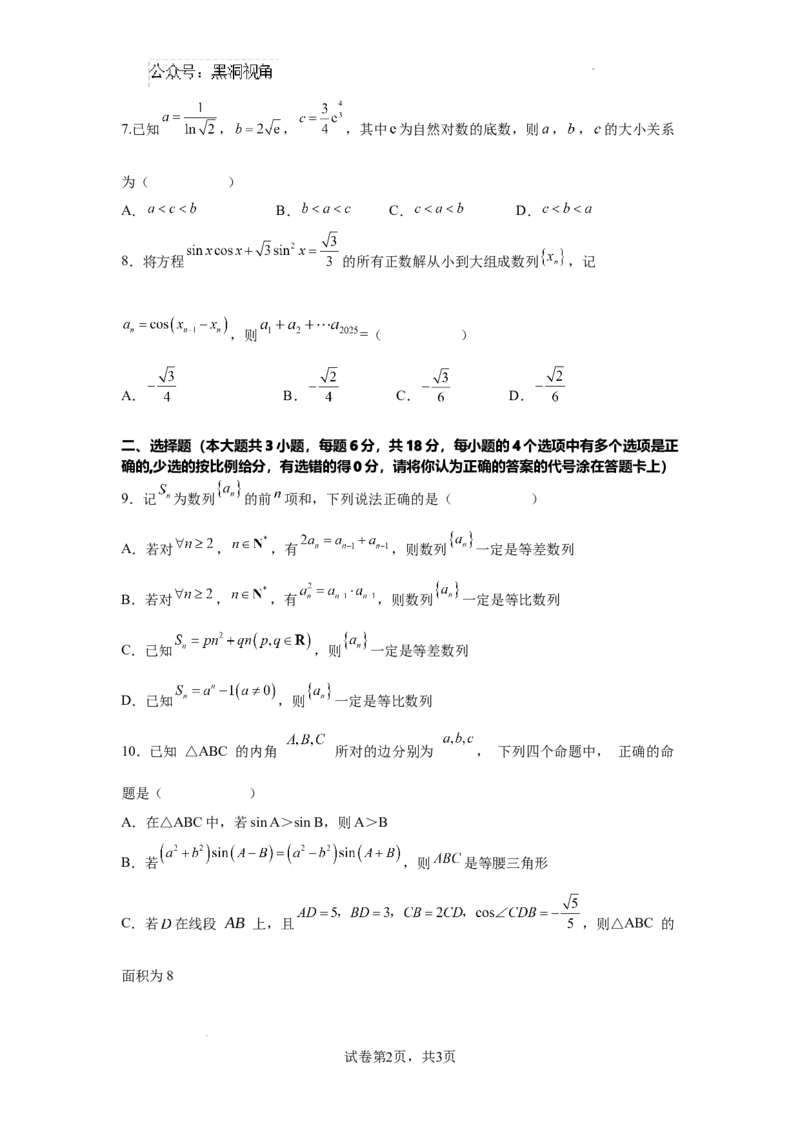文档内容
红岭中学(红岭教育集团)2025 届高三第二次统一考试
数 学
(说明:本试卷考试时间为120分钟,满分为150分)
一、选择题(本大题共8小题,每题5分,共40分,每小题的4个选项中仅有一个选项
是正确的,请将你认为正确的答案的代号涂在答题卡上)
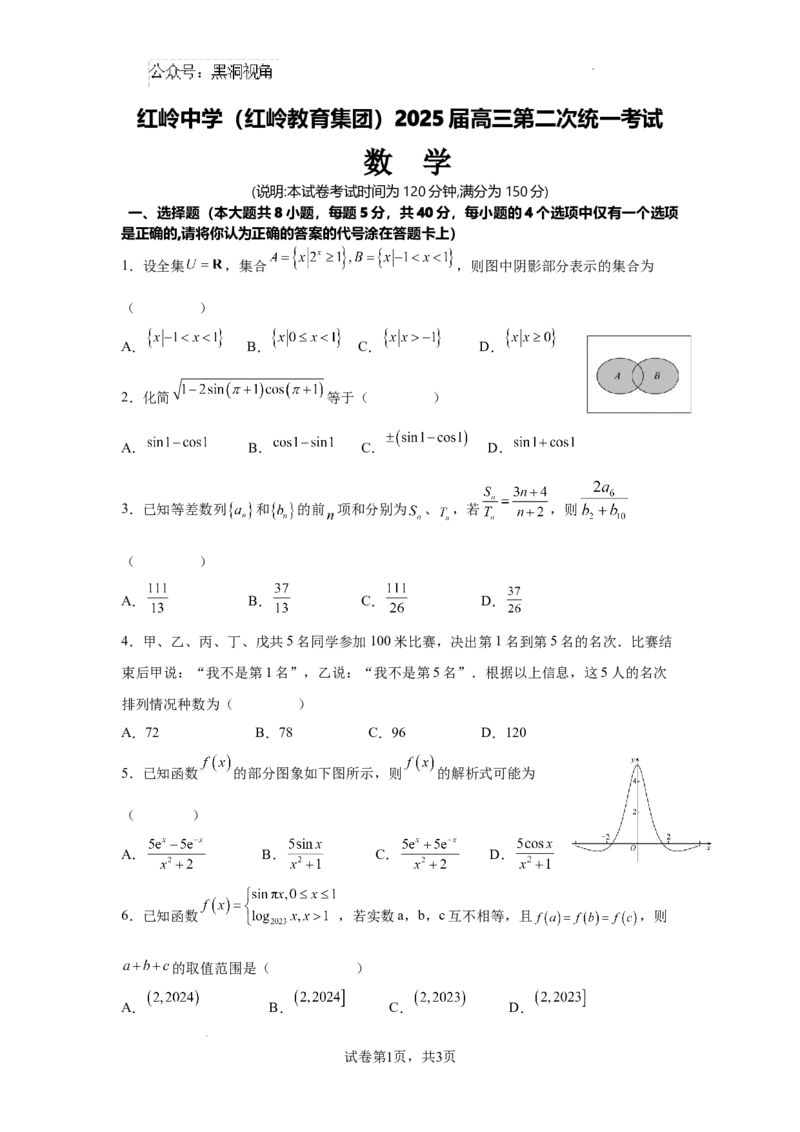
1.设全集 ,集合 ,则图中阴影部分表示的集合为
( )
A. B. C. D.
2.化简 等于( )
A. B. C. D.
3.已知等差数列 和 的前 项和分别为 、 ,若 ,则
( )
A. B. C. D.
4.甲、乙、丙、丁、戊共5名同学参加100米比赛,决出第1名到第5名的名次.比赛结
束后甲说:“我不是第1名”,乙说:“我不是第5名”.根据以上信息,这5人的名次
排列情况种数为( )
A.72 B.78 C.96 D.120
5.已知函数 的部分图象如下图所示,则 的解析式可能为
( )
A. B. C. D.
6.已知函数 ,若实数a,b,c互不相等,且 ,则
的取值范围是( )
A. B. C. D.
试卷第1页,共3页
学科网(北京)股份有限公司7.已知 , , ,其中 为自然对数的底数,则 , , 的大小关系
为( )
A. B. C. D.
8.将方程 的所有正数解从小到大组成数列 ,记
,则 =( )
A. B. C. D.
二、选择题(本大题共3小题,每题6分,共18分,每小题的4个选项中有多个选项是正
确的,少选的按比例给分,有选错的得0分,请将你认为正确的答案的代号涂在答题卡上)
9.记 为数列 的前 项和,下列说法正确的是( )
A.若对 , ,有 ,则数列 一定是等差数列
B.若对 , ,有 ,则数列 一定是等比数列
C.已知 ,则 一定是等差数列
D.已知 ,则 一定是等比数列
10.已知 △ABC 的内角 所对的边分别为 , 下列四个命题中, 正确的命
题是( )
A.在△ABC中,若sin A>sin B,则A>B
B.若 ,则 是等腰三角形
C.若 在线段 AB 上,且 ,则△ABC 的
面积为8
试卷第2页,共3页
学科网(北京)股份有限公司D.若 ,动点 在△ABC 所在平面内且 ,则 动点 的轨迹的
长度为
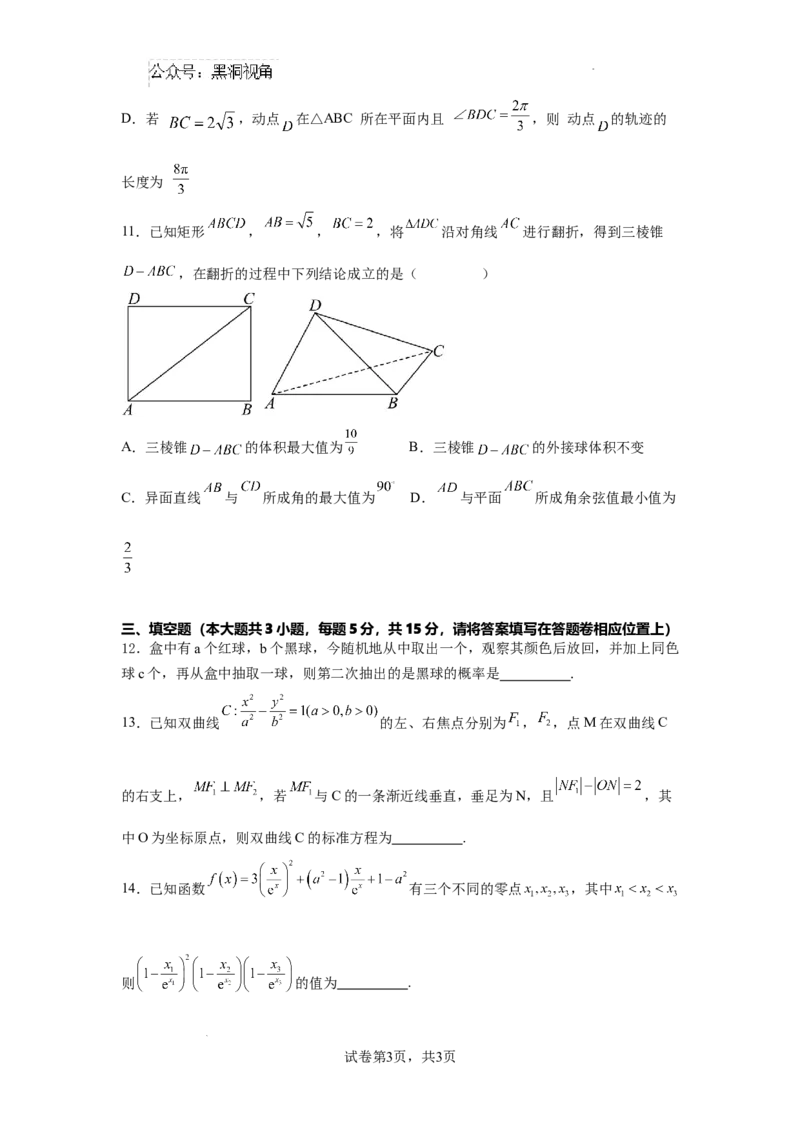
11.已知矩形 , , ,将 沿对角线 进行翻折,得到三棱锥
,在翻折的过程中下列结论成立的是( )
A.三棱锥 的体积最大值为 B.三棱锥 的外接球体积不变
C.异面直线 与 所成角的最大值为 D. 与平面 所成角余弦值最小值为
三、填空题(本大题共3小题,每题5分,共15分,请将答案填写在答题卷相应位置上)
12.盒中有a个红球,b个黑球,今随机地从中取出一个,观察其颜色后放回,并加上同色
球c个,再从盒中抽取一球,则第二次抽出的是黑球的概率是 .
13.已知双曲线 的左、右焦点分别为 , ,点M在双曲线C
的右支上, ,若 与C的一条渐近线垂直,垂足为N,且 ,其
中O为坐标原点,则双曲线C的标准方程为 .
14.已知函数 有三个不同的零点 ,其中
则 的值为 .
试卷第3页,共3页
学科网(北京)股份有限公司四、解答题(共77分,请将答案填写在答题卷相应位置上,答错位置不给分,要求要有必
要的文字叙述和推理说明)
15.(本小题13分)
设正项数列 的前n项和为 ,且 ,当 时, .
(1)求数列 的通项公式;
(2)设数列 满足 ,且 ,求数列 的通项公式.
16.(本小题15分)
如图, 、 、 为圆锥三条母线, .
(1)证明: ;
(2)若圆锥侧面积为 为底面直径, ,求平面PAB和平面PAC所成角的余弦
值.
17.(本小题15分)
已知椭圆 : 的离心率为 ,右顶点 与 的上,下顶点所围成的三
角形面积为 .
(1)求 的方程;
(2)不过点 的动直线 与 交于 , 两点,直线 与 的斜率之积恒为 ,证明直线
过定点,并求出这个定点.
试卷第4页,共3页
学科网(北京)股份有限公司18.(本小题17分)
已知函数 .
(1)若 的极大值为 ,求 的值;
(2)当 时,若 , 使得 ,求 的取值范围.
19.(本小题17分)
法国数学家费马在给意大利数学家托里拆利的一封信中提到“费马点”,即平面内到三角
形三个顶点距离之和最小的点,托里拆利确定费马点的方法如下:
当 的三个内角均小于 时,满足 的点 为
① 120∘ ∠AOB=∠BOC=∠COA=120∘ O
费马点;
当 有一个内角大于或等于 时,最大内角的顶点为费马点.
② 120∘
请用以上知识解决下面的问题:
已知 的内角 所对的边分别为 ,点 为 的费马点,且
A,B,C a,b,c M
cos2A+cos2B−cos2C=1.
(1)求C;
(2)若c=4,求|MA|⋅|MB|+|MB|⋅|MC|+|MC|⋅|MA|的最大值;
(3)若|MA|+|MB|=t|MC|,求实数t的最小值.
试卷第5页,共3页
学科网(北京)股份有限公司