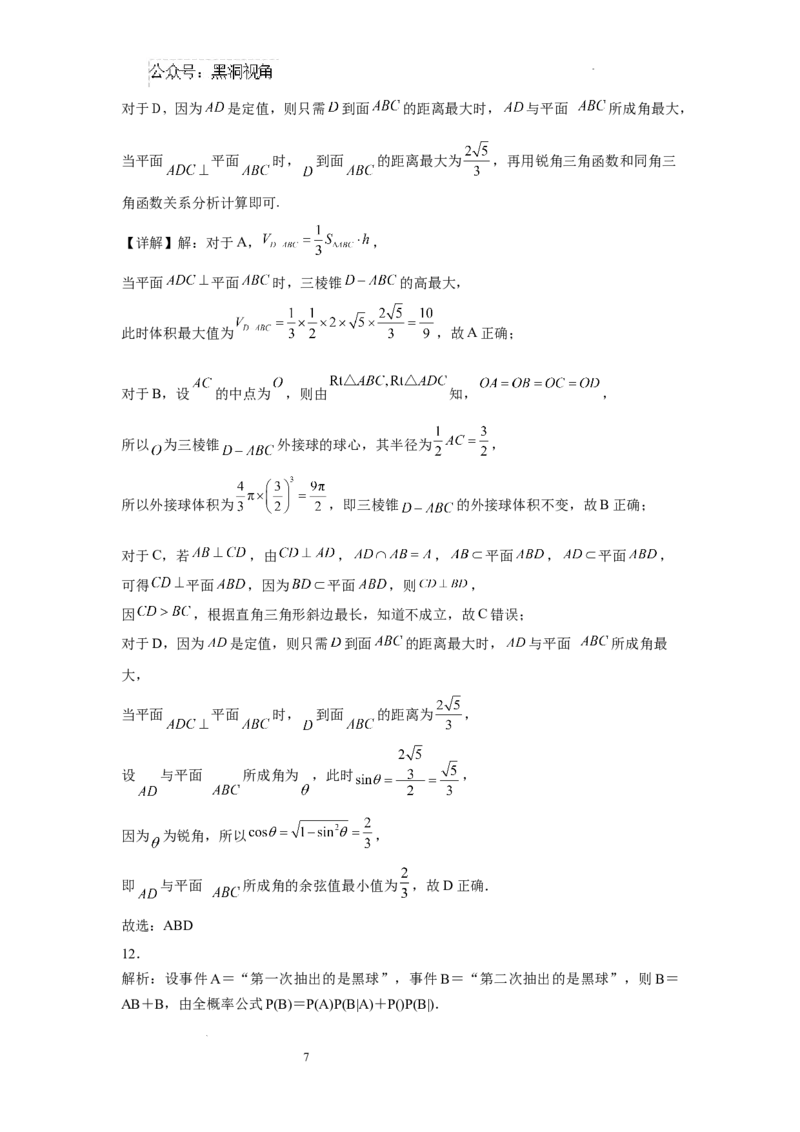文档内容
红岭中学(红岭教育集团)2025 届高三第二次统一考试
数学参考答案
(说明:本试卷考试时间为120分钟,满分为150分)
1 2 3 4 5 6 7 8 9 10 11
C A B B D A C C AC ACD ABD
1.C
2.A
【分析】利用同角三角函数的基本关系式,结合三角函数值的符号,化简所求表达式.
【详解】依题意,原式
①.
由于 ,所以 ,故①可化为
. 故选:A.
【点睛】本小题主要考查同角三角函数的基本关系式,考查诱导公式,考查三角函数值在
各个象限的符号,考查化归与转化的数学思想方法,属于基础题.
3.B
【详解】设等差数列 的公差为 ,则
因为等差数列 和 的前 项和分别为 、 ,满足 ,
, 故选:B
4.B
【分析】讨论甲是否在第5名,根据排列组合公式计算即可.
【详解】当甲是第5名时,共有 种;
当甲不是第5名时,共有 种;
综上,共有78种. 故选:B
5.D
1
学科网(北京)股份有限公司【分析】由图知函数为偶函数,应用排除,先判断B中函数的奇偶性,再判断A、C中函
数在 上的函数符号排除选项,即得答案.
【详解】由图知:函数图象关于y轴对称,其为偶函数,且 ,
由 且定义域为R,即B中函数为奇函数,排除;
当 时 、 ,即A、C中 上函数值为正,排除;
故选:D
6.A
【分析】根据函数的解析式作出函数的图象,根据 结合函数的对称性可得
及 的范围,从而求解 的范围.
【详解】作出函数 的图象如图:
设 ,且 ,
则函数 与直线 的三个交点从左到右依次为
, , ,
则点 与 在函数 上,而函数 的图象关于直线 对
称,
所以 ,由 得 ,
若满足 ,则 ,所以 ,
所以 ,即 的取值范围是 . 故选:A.
7. C
2
学科网(北京)股份有限公司【解析】构造函数 ,得 , , , .
当 时, ,当 时, ,所以 在 上单调递减,
上单调递增.
易知 ,所以 ,所以 .
又 ,因为 ,所以 ,所以 .
所以 .
8.C
3
学科网(北京)股份有限公司9.AC
【分析】利用等差,等比数列的定义和性质,以及等差,等比数列的前 项和的形式,可
逐一判断.
【详解】由 和等差中项的性质,可得数列 是等差数列,即A正
确;
当 时,由 和等比中项的性质,
可得数列 是等比数列,即B不正确;
4
学科网(北京)股份有限公司由等差数列前 项和 ,
得 可看成 的二次函数,且不含常数项,则C正确;
由等比数列前 项和 ,
若 ,则 ,所以 ,则此时数列 不是等比数列,则D错.故选:AC
10.ACD
【分析】化简条件得到 ,求得 或 ,可判定B不正确;设
,在 中,利用余弦定理求得 ,得到 ,求得
和 ,结合面积公式,可判定C正确;根据题意得到点 在以 为弦的一个圆上,
结合正弦定理和圆的性质,以及弧长公式,可判定D正确.
【详解】对于A中,由正弦定理可知A正确;
对于B中,由 ,
可得 ,
整理得 ,
由正弦定理得 ,可得 ,
因为 ,可得 或 ,即 或 ,
所以 是等腰三角形或直角三角形,所以B不正确;
对于C中,由 在线段 上,且 , , , ,
则 ,设 ,
在 中,利用余弦定理 ,
整理得 ,解得 或 (舍去),
5
学科网(北京)股份有限公司所以 ,
在 中,可得 ,
在 中,由余弦定理可得 ,
,所以 ,
所以 的面积为 ,所以C正确;
对于D中,在 中,因为 , ,
则点 在以 为弦的一个圆上,
由正弦定理可得 外接圆的直径为 ,即 ,
当点 在 外部时,如图所示,
因为 ,可得 ,所以 ,
所以 的长度为 ,
同理,当点在 内部时,可得对应的弧长也是 ,
所以动点 的轨迹的长度为 ,故D正确.
故选:ACD.
11.ABD
【分析】对于A, 当平面 平面 时,三棱锥 的高最大,再棱锥体积公
式计算即可;
对于B,设 的中点为 ,则由 知, ,所以 为
三棱锥 外接球的球心,其半径为 ,再用球的体积公式计算即可;
对于C,若 ,由 , , 平面 , 平面 ,
可得 平面 ,得到 ,因为 ,直角三角形斜边最长,知道不成立;
6
学科网(北京)股份有限公司对于D, 因为 是定值,则只需 到面 的距离最大时, 与平面 所成角最大,
当平面 平面 时, 到面 的距离最大为 ,再用锐角三角函数和同角三
角函数关系分析计算即可.
【详解】解:对于A, ,
当平面 平面 时,三棱锥 的高最大,
此时体积最大值为 ,故A正确;
对于B,设 的中点为 ,则由 知, ,
所以 为三棱锥 外接球的球心,其半径为 ,
所以外接球体积为 ,即三棱锥 的外接球体积不变,故B正确;
对于C,若 ,由 , , 平面 , 平面 ,
可得 平面 ,因为 平面 ,则 ,
因 ,根据直角三角形斜边最长,知道不成立,故C错误;
对于D,因为 是定值,则只需 到面 的距离最大时, 与平面 所成角最
大,
当平面 平面 时, 到面 的距离为 ,
设 与平面 所成角为 ,此时 ,
因为 为锐角,所以 ,
即 与平面 所成角的余弦值最小值为 ,故D正确.
故选:ABD
12.
解析:设事件A=“第一次抽出的是黑球”,事件B=“第二次抽出的是黑球”,则B=
AB+B,由全概率公式P(B)=P(A)P(B|A)+P()P(B|).
7
学科网(北京)股份有限公司由题意P(A)=,P(B|A)=,
P()=,P(B|)=,
所以P(B)=+=.
13.
【分析】利用中位线的性质得到 ,且 ,根据 得到
,然后利用点到直线的距离公式得到 ,最后再直角三角形 中利用勾股
定理列方程得到 ,即可得到双曲线方程.
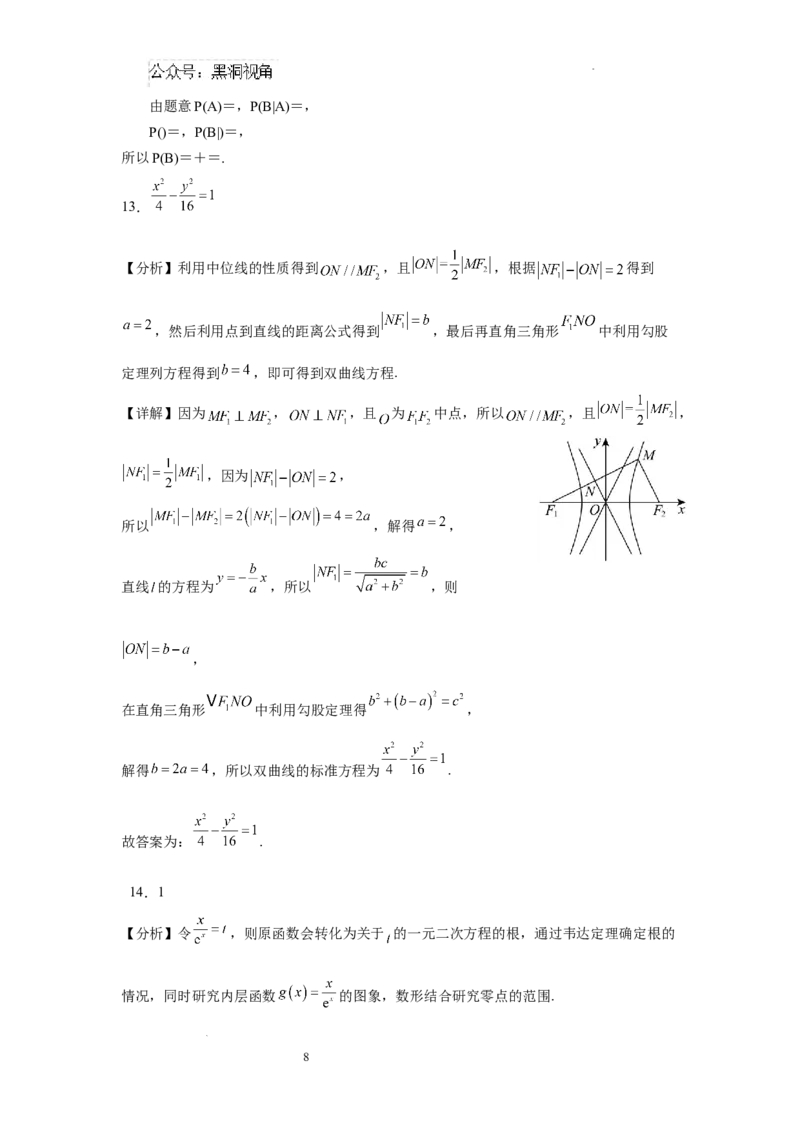
【详解】因为 , ,且 为 中点,所以 ,且 ,
,因为 ,
所以 ,解得 ,
直线 的方程为 ,所以 ,则
,
在直角三角形 中利用勾股定理得 ,
解得 ,所以双曲线的标准方程为 .
故答案为: .
14.1
【分析】令 ,则原函数会转化为关于 的一元二次方程的根,通过韦达定理确定根的
情况,同时研究内层函数 的图象,数形结合研究零点的范围.
8
学科网(北京)股份有限公司【详解】设 ,
,
当 时, ;
当 时, ,
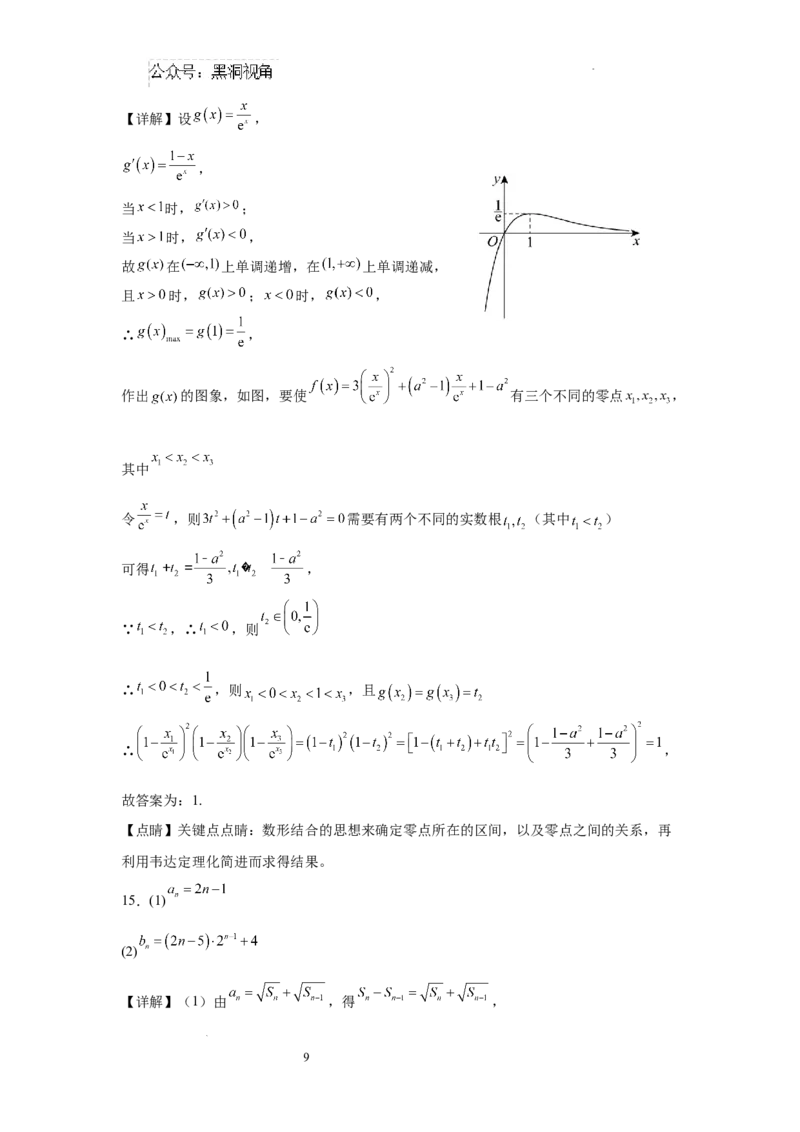
故 在 上单调递增,在 上单调递减,
且 时, ; 时, ,
∴ ,
作出 的图象,如图,要使 有三个不同的零点 ,
其中
令 ,则 需要有两个不同的实数根 (其中 )
可得 ,
∵ ,∴ ,则
∴ ,则 ,且
∴ ,
故答案为:1.
【点睛】关键点点睛:数形结合的思想来确定零点所在的区间,以及零点之间的关系,再
利用韦达定理化简进而求得结果。
15.(1)
(2)
【详解】(1)由 ,得 ,
9
学科网(北京)股份有限公司因为 ,所以 ,
所以 是以 为首项,1为公差的等差数列,所以 ,
所以,当 时, ,
当 时, 也满足上式,
所以数列 的通项公式为 .
(2)由 知:
当 时, ,
①,
则 ②,
由 得: ,
化简得: ,
当 时, 也满足上式,
所以数列 的通项公式为 .
16.(1)证明见解析
(2)
【分析】(1)取 中点 ,连接 、 ,则 ,故可得 面
,从而得到 .
(2)利用向量法可求面 、面 的法向量,计算出它们的夹角的余弦值后可得二面
角的余弦值.
【详解】(1)取 中点 ,连接 、 ,
10
学科网(北京)股份有限公司因为 ,所以 ,
又因为 面 面 ,所以 面 ,
因为 面 ,所以 .
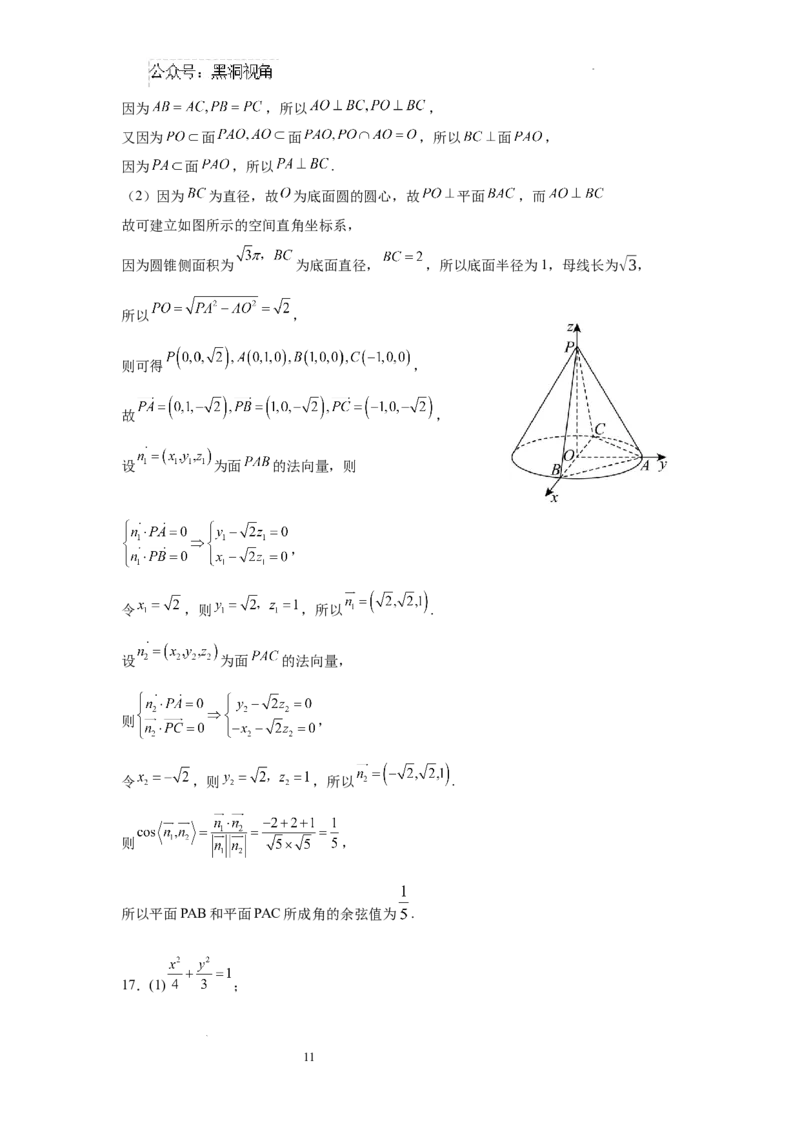
(2)因为 为直径,故 为底面圆的圆心,故 平面 ,而
故可建立如图所示的空间直角坐标系,
因为圆锥侧面积为 为底面直径, ,所以底面半径为1,母线长为√3,
所以 ,
则可得 ,
故 ,
设 为面 的法向量,则
,
令 ,则 ,所以 .
设 为面 的法向量,
则 ,
令 ,则 ,所以 .
则 ,
所以平面PAB和平面PAC所成角的余弦值为 .
17.(1) ;
11
学科网(北京)股份有限公司(2)(i)证明见解析;(ii) .
【分析】(1)根据椭圆的离心率及三角形面积,列出方程组求解即得.
(2)(i)设出直线 的方程,与椭圆方程联立,利用斜率坐标公式,结合韦达定理推理即
得;(ii)由(i)的信息,借助三角形面积建立函数关系,再求出最大值.
【详解】(1)令椭圆 的半焦距为c,由离心率为 ,得 ,解得
,
由三角形面积为 ,得 ,则 , ,
所以 的方程是 .
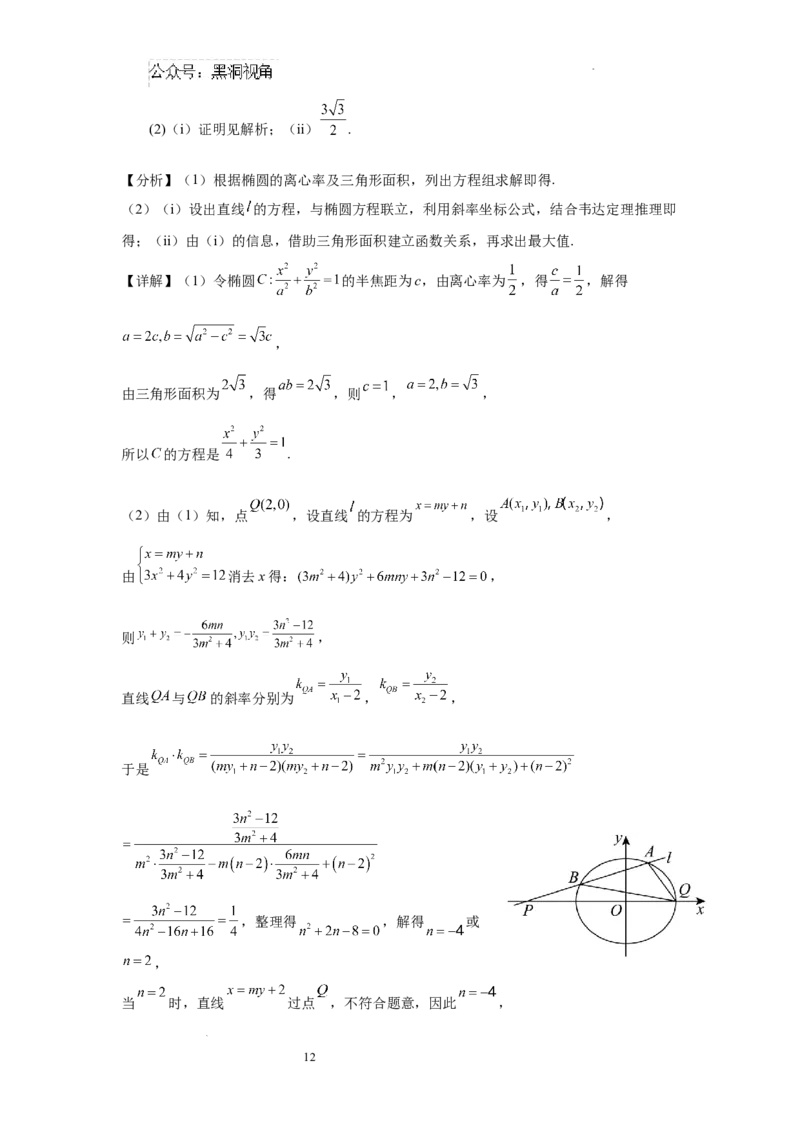
(2)由(1)知,点 ,设直线 的方程为 ,设 ,
由 消去x得: ,
则 ,
直线 与 的斜率分别为 , ,
于是
,整理得 ,解得 或
,
当 时,直线 过点 ,不符合题意,因此 ,
12
学科网(北京)股份有限公司直线 : 恒过定点 .
【点睛】思路点睛:圆锥曲线中的几何图形面积范围或最值问题,可以以直线的斜率、
横(纵)截距、图形上动点的横(纵)坐标为变量,建立函数关系求解作答.
18.(1) ;(2)
【分析】(1)对函数求导后,由 ,得 或 ,然后分 ,
和 三种情况讨论导数的正负,从而可求出函数的单调区间和极值,使极大
值为 可求出 ;
(2)将问题转化为 在 上的值域是 在 的值域的子集,由
(2)知 在 上单调递增,在 上单调递减,在 上单调递增,然
后分 , 和 三种情况讨论即可.
【详解】(1) ,
因为 ,令 ,解得 或 ,
①当 时,即 时, 在 上单调递增,
在 上单调递减,在 上单调递增,
所以 的极大值为 ,不符合题意;
②当 时,即 时, , 在R上单调递增,无极大值;
③当 时,即 时, 在 上单调递增,
在 上单调递减,在 上单调递增,
所以 极大值为 , ,符合题意.
13
学科网(北京)股份有限公司综上所述, .
(2)由题意得当 时, 在 上的值域是 在 的值域的子集,
由(2)知, 在 上单调递增,在 上单调递减,在 上单调递增,
且当 时, ,当 时, ,
①当 时,即 时,当 时, 单调递增, ,
又因为当 时, ,
因为 ,所以当 时, 使得 ,
②当 时,即 时,
当 时, 单调递增, ,
当 时, ,
若满足题意,只需 ,即 ,
③当 时,即 时,
当 时, 在 上单调递减, 上单调递增,
所以函数 的最小值为 ,所以 ,
又因为 时, ,
若满足题意,只需 ,即 ,
因为 ,所以 ,所以无解,所以 不合题意
综上,实数 的取值范围为 .
【点睛】关键点点睛:此题第(3)问解题的关键是转化问题为当 时, 在
14
学科网(北京)股份有限公司上的值域是 在 的值域的子集,进一步转化求函数的值域问题,
从而得解.
19.解:(1)因为cos2A+cos2B−cos2C=1,
所 以 1−2sin2A+1−2sin2B−1+2sin2C=1, 即
sin2A+sin2B=sin2C,
由正弦定理得a2+b2=c2.
所以C=90∘.
(2)由(1)知C=90∘,所以▵ABC的三个角都小于120∘,
因为点M为▵ABC的费马点,所以∠AMB=∠BMC=∠CMA=120∘.
由S =S +S +S 得:
▵ABC ▵AMB ▵BMC ▵CMA
1 1 1 1
ab= |MA|⋅|MB|sin120∘+ |MB|⋅|MC|sin120∘+ |MC|⋅|MA|sin120∘,
2 2 2 2
2√3
整理得|MA|⋅|MB|+|MB|⋅|MC|+|MC|⋅|MA|= ab .
3
又因为c2=a2+b2=16≥2ab,所以ab≤8,当且仅当a=b时等号成立.
2√3 16√3
所以|MA|⋅|MB|+|MB|⋅|MC|+|MC|⋅|MA|= ab≤ ,
3 3
16√3
所以|MA|⋅|MB|+|MB|⋅|MC|+|MC|⋅|MA|的最大值为 .
3
(3)由(2)知∠AMB=∠BMC=∠CMA=120∘.
设|MC|=x,|MA|=mx,|MB|=nx,(x>0,m>0,n>0),
由|MA|+|MB|=t|MC|得m+n=t.
由余弦定理得:
在 中, ,
△ACM |AC|2=x2+m2x2−2mx2cos120∘=(m2+m+1)x2
在 中, ,
▵BCM |BC|2=x2+n2x2−2nx2cos120∘=(n2+n+1)x2
在 中, ,
▵ABM |AB|2=m2x2+n2x2−2mnx2cos120∘=(m2+n2+mn)x2
因为|AC|2+|BC|2=|AB|2,
所以 ,
(m2+m+1)x2+(n2+n+1)x2=(m2+n2+mn)x2
整理得m+n+2=mn.
15
学科网(北京)股份有限公司因为 (m+n) 2,当且仅当 时等号成立,
m+n+2=mn≤ m=n
2
所以 (t ) 2,整理得 ,
t+2≤ t2−4t−8≥0
2
解得t≥2+2√3或者t≤2−2√3(舍去), 所以实数t的最小值为2+2√3.
16
学科网(北京)股份有限公司