文档内容
2024年普通高等学校招生全国统一考试
高考模拟调研卷数学(二)
数学测试卷共 4页,满分 150分。考试时间120分钟。
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 已知集合 则 =
A. B. C. D.
2. 双曲线 的渐近线方程为
3. 已知正方形 的边长为2, 为 中点, 则
B. C. D.
4 展开式中的常数项为
A. -2 B. 0 C. 2 D. 6
5. 若复数 满足 ,则称复数 的循环常数为 . 的最
小循环常数为
A. 2 B. 3 C.4 D. 6
6. 已知 则
A. B.
7. 已知函数 且 则
A. B. C. 1 D.
8. 已知 则 的大小关系为
A. B. C. D.
二、选择题:本题共4小题,每小题5分,共 20分 .在每小题给出的选项中,有多项符合题目要求。全部选对的
得5分,部分选对的得2分,有选错的得0分。9. 某班主任为了解本班学生上学时间,抽取了12名学生早晨从家到学校的时长,得到如下数据(单位:分):
20,18, 23, 27,32, 21, 26, 23, 12, 17, 19, 20, 则下列说法正确的是
A. 这组数据的中位数是20.5 B. 这组数据的上四分位数是23
C. 这组数据的平均数是21.5 D. 这组数据的极差是20
10. 已知函数 , 则下列四个结论中正确的是
A. 是偶函数 B. 的图象关于直线x=π对称
C. 的最小正周期为 D. 的值域为
11. 已知平行六面体 的所有棱长均为1, 则下列说法正
确的有
A.直线 与直线 夹角的余弦值为 B. 直线 平面
C.四面体 外接球的表面积为 D. 点 到平面 的距离为
12.如图,在等腰直角三角形 中, ,过点 的光线经 边上点 反射到 上的点
,若 ,则下列结论正确的有
A. 为 中点 B.
D
C.
三、填空题:本题共4小题,每小题5分,共20分。
13. 某班在一次联欢会中进行一项抽奖游戏,规则如下:先在 2种方法中随机选择一个,第一种方法,连续抛
掷3次质地均匀的硬币,如3次掷出相同面,则为一等奖,如有2次相同,则为二等奖,其余为三等奖;
第二种方法,从标有1,2,3数字的质地大小相同的 3个小球中有放回地抽取3次,如3次抽取数字都相
同,为一等奖,如有2次相同,为二等奖,其余为三等奖。则在一次抽奖活动中,获得一等奖的概率为
.
14. 已知椭圆 的左、右焦点分别为 , ,直线 经过 且垂直于 轴,
与 相交于 两点. 若 是周长为12的正三角形, 则 =_________.
15. 已知函数 满足: ① 的图象过点 ; ② 是偶函数; ③对任意的非零实数
请写出一个满足上述条件的函数 = .
16. 已知直四棱柱 的底面是边长为4的菱形, ,侧棱长为 , 点 为的中点,点 在直四棱柱. 的表面上运动,且 ,则 的中点
的轨迹的长度为__________.
四、解答题:本题共6小题,共 70分。解答应写出文字说明、证明过程或演算步骤。
17. (10分)
在 中, 角 的对边分别是 已知 且平面向量
满足
(1) 求角 的大小:
(2) 若边 的中线长为 . 求 的面积.
18. (12分)
篮球世界杯于 2023年9月 10日在菲律宾马尼拉圆满结束,德国男篮凭借出色表现连续击败美国、塞尔维亚
夺得冠军,德国也成为阿根廷、西班牙之后又一支在足球、篮球世界大赛中都夺得冠军的国家。重庆市某中学对
学生对于篮球的喜爱情况进行调查,将每周打篮球或观看篮球比赛超过5小时的学生称为“篮球迷”,否则称为
“非篮球迷”,从调查结果中随机抽取100人进行分析,抽取的女生人数是男生人数的 ;抽取的男生中“非篮
球迷”人数是“篮球迷”入数的 。抽取的女生中“篮球迷”人数是“非篮球迷”人数的 .
篮球迷 非篮球迷 总计
男生
女生
总计
(1)完成列联表,并依据小概率值 的独立性检验,能否认为是否为 “篮球迷”与性别有关联?
(2) 现从抽取的男生中,按是否为“篮球迷”比例采用分层抽样的方法抽取 5人参加篮球知识闯关比赛,已
知其中 “篮球迷”。“非篮球迷”独立闯关成功的概率分别为 , ;在恰有两人闯关成功的条件下,求
有“篮球迷”闯关成功的概率.
参考数据与公式:
0.10 0.05 0.010 0.001
2.706 3.841 6.635 10.828
其中19. (12分)
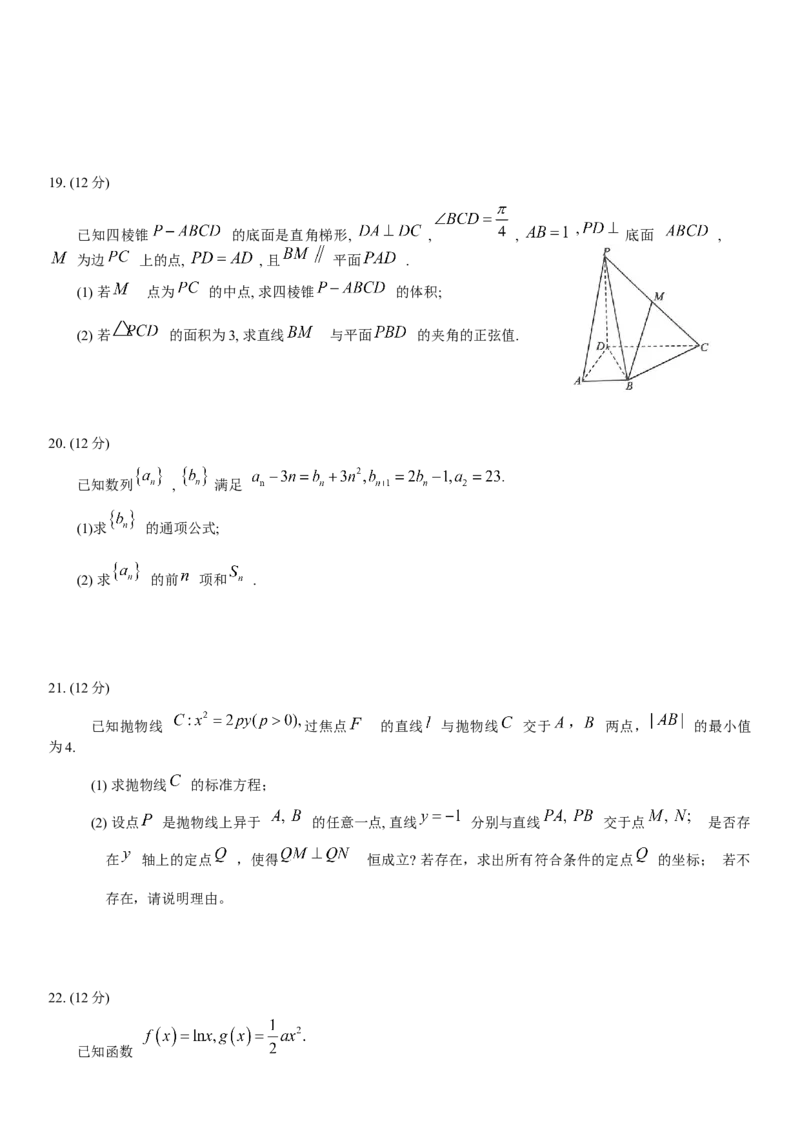
已知四棱锥 的底面是直角梯形, , , 底面 ,
为边 上的点, , 且 平面 .
(1) 若 点为 的中点, 求四棱锥 的体积;
(2) 若 的面积为3, 求直线 与平面 的夹角的正弦值.
20. (12分)
已知数列 , 满足
(1)求 的通项公式;
(2) 求 的前 项和 .
21. (12分)
已知抛物线 过焦点 的直线 与抛物线 交于 两点, 的最小值
为4.
(1) 求抛物线 的标准方程;
(2) 设点 是抛物线上异于 的任意一点, 直线 分别与直线 交于点 是否存
在 轴上的定点 ,使得 恒成立? 若存在,求出所有符合条件的定点 的坐标; 若不
存在,请说明理由。
22. (12分)
已知函数(1) 若方程 有2个实数根, 求实数 的取值范围;
(2)若方程 有2个实数根. 且不等式 对任意 恒成立,求
正数 的取值范围( 为自然对数的底数).