文档内容
届 月份考试·数学 第 页 共 页 届 月份考试·数学 第 页 共 页
2025 3 1 ( 4 ) 2025 3 2 ( 4 )
届 月份考试 二、选择题:本题共 小题,每小题 分,共 分.在每小题给出的选项中,有多项符合题目要求.全 3 6 18 2025 3 部选对得 分,部分选对的得部分分,有选错的得 分. 数 学 6 0 .已知实数a b c满足a b c 则下列不等式不一定成立的是 试卷满分: 分 考试时间: 分钟 9 , , > > >0, 150 120 b c b a b 注意事项: + ba ab - a c 1 答卷前, 考生务必将自己的姓名、 考生号等填写在答题卡和试卷指定位置。 A.a + c> a B. > C.lg b - c>0 D. + + bc >2 2 1. 回答选择题时, 选出每小题答案后, 用 铅笔把答题卡上对应题目的答案标号涂黑。 .已知函数f x x x 则下列说法正确的是 2. 2B 10 ( )= -sin +sin3 , 如需改动, 用橡皮擦干净后, 再选涂其他答案标号。 回答非选择题时, 将答案写在答题卡上。 此函数的周期为 此函数图象关于直线x π对称 写在本试卷上无效。 A. π B. = 2 考试结束后, 将本试卷和答题卡一并交回。 ( ) 3. 此函数在区间 上有 个零点 此函数在区间 π π 上单调递减 一、选择题:本题共 小题,每小题 分,共 分 在每小题给出的四个选项中,只有一个选项是正 C. [0,2π] 7 D. , 8 5 40 . 4 2 确的 .一个圆柱表面积为S 体积为V 则下列四组数对中 可作为数对 S V 的有 . 11 , , , ( , ) { } .已知集合A x 3 B { } 则A B A.(4π,π) B.(5π,π) C.(5,1) D.(6,1) 1 = x >1 , = -1,0,1,2,3 , ∩ = 三、填空题:本题共 小题,每小题 分,共 分. 3 5 15 { } { } { } { } A. 1,2 B. 1,2,3 C. -1,1,2 D. -1,0,1,2 .已知 a 是等比数列 且a a 则a . .已知i为虚数单位 若z( i) i 则 z i 12 { n} , 2=1, 6=8, 4= 2 , 2+ =3- , +2 = .若圆C x2 y2 r2 (r )与曲线y x 有两个公共点 则r的取值范围为 . 13 : + = >0 =4-2 , A. 5 B.5 C. 10 D.10 .已知 x 表示不超过x的最大的整数 如 . 若方程 x2 x 的正实数根 14 [ ] , [π]=3,[-1 3]=-2, - -1=0 .已知向量a b x 若a a b 则x 3 =(-1,2), =(3, ), ∥( + ), = 为m 则 m12 . , [ ]= 3 3 四、解答题:本题共 小题,共 分.解答应写出文字说明、证明过程或演算步骤. A.- B. C.-6 D.6 5 77 2 2 . 分 ABC的内角A B C的对边分别为a b c 已知 B C B A. .已知 (α β) (α β) α β 则 (α β) 15 (13 )Δ , , , , , sin( - )=sin -sin 4 sin - =3cos + ,tan tan =2, tan - = 求C (1) ; 1 1 A.-1 B.- C. D.1 若c ABC的面积为 .求 ABC的周长. 2 2 (2) =2 3,Δ 2 3 Δ .已知抛物线y mx2 m 的焦点为F 第一象限的点P n 在抛物线上 若 FP 则m n 5 = ( >0) , ( ,1) , =2, + = 4 2 9 9 A. B. C. D. 9 9 2 4 S .已知数列{a }的前n项和为S a 且{nS }为等差数列 若S a a a 则 8 6 n n, 1=2, n , 6+ 4+ 5+ 6=1, a = 8 A.36 B.-36 C.63 D.-63 x2 y2 .设双曲线C 的左 右焦点分别为 F F 坐标原点为 O 第一象限的点 P 在双曲线 C 7 : - =1 、 1, 2, , 9 16 上 连接PO并延长交双曲线另一点Q 若 F P F Q 则 PQ , , 1 =3 1 , = A.4 7 B.4 5 C.8 D.4 3 .已知函数f x 的定义域为R x R 都有 f x f x x f x f x x 且 f 8 ( ) ,∀ ∈ , : ( +1)- ( )≥ , ( +2)- ( )≤2 +1, (1)= 1, 则f (41)= A.820 B.821 C.1 600 D.1 6011 1 6 7 . . ( ( ( ( ( ( 1 1 2 1 1 2 5 5 ) ) ) ) 求 若 求 求 分 分 证 证 数 ) ) A 如 数 1 : : 列 C 平 数 图 列 = { 面 列 n 2 { , a A 在 a { n C A n } a } 三 1 = 的 n B 满 + 2 棱 C 前 1 B 足 ⊥ } 柱 C 是 n , 平 a 求 A 项 1 等 面 = B 直 和 C 比 - A - 3 线 数 B S , A n C a 1 列 A . B n ; + B 1 1 ; C 1 = 1 与 - 中 A 2 平 a , A C n 面 B 1 - C 3 B ⊥ . C C 1 平 C 1 面 B 1 A 所 C B 成 C 1 角 B A 1 1, 的 A 正 1 C 弦 ⊥ 值 AB . . 1 1 8 9 . . ( ( ( ( ( 重 ( ( 1 1 2 3 1 1 2 合 7 7 ) ) ) ) ) 若 讨 当 求 已 ( ( 分 分 ) ⅰ ⅱ , 论 知 ) ) a a C 满 ) ) 已 已 < = 不 的 求 求 f 0 足 2 ( 知 知 在 x , 方 时 证 四 直 ) 求 函 椭 的 程 , : 边 x 线 曲 f ∠ 数 圆 轴 ( 单 ; 形 x 线 T P 上 f ) C 调 A B ( A ≤ : , x y Q 的 P 性 a x T ) = b B 2 2 B 为 动 = - ; f + Q ( l 的 y b 钝 n 2 1 x 点 面 2 2 ( ) a 斜 角 = 在 - 积 x M a 1 2 率 ; 点 - ) 的 ( 在 a ( - 之 ( 1 最 > a 定 1 + 积 b , 恒 大 a 直 > f 等 ) ( 成 0 值 线 x 1 ) 于 + ) 立 . 的 l x ) n - , 处 = x 左 求 4 3 ( 4 的 a 、 . 实 上 ∈ 右 当 切 数 运 R 顶 点 线 ) 动 点 b . 方 T 的 时 分 在 程 最 , 别 椭 直 ; 小 为 圆 线 值 的 A A . , M 上 B 、 . 顶 B 椭 M 点 圆 分 时 上 别 , 任 Δ 交 A 意 T 椭 B 一 圆 的 点 于 面 T 两 积 ( 不 点 为 与 P 2 , A Q 3 , . . B
届 月份考试·数学 第 页 共 页 届 月份考试·数学 第 页 共 页
2025 3 3 ( 4 ) 2025 3 4 ( 4 )届 月份考试 b c b
即 + 故 一定成立
2025 3 a c> a, A ;
数学 参考答案 +
对于选项 取a b 显然ba ab 故 不一定成立
B, =4, =2, = , B ;
x a b
. 【详解】 由3 得3 3- 即 x 所以A B { }.故选 . 对于选项 取a b c 显然 - 故 不一定成立
1 A x >1, x -1= x >0, 0< <3, ∩ = 1,2 :A C, =3, =2, =1, lg b c=0, C ;
-
i ( i)( i)
. 【详解】 z 3- 3- 2- i 故z i 所以 z i i .故选 对于选项 a c 1 b c 1 bc 1 故 一定成立 故选
2 C =
2+
i=(
2+
i)(
2-
i) =1- , =1+ , +2 = 1+3 = 10 :C. D, + + bc> + + bc>2 + bc≥2 2, D . :BC.
3
.
C
【详解】 因为a
∥(
a
+
b
),
所以a
∥
b
,
所以
-1×
x
=2×3,
即x
=-6
.故选
:C. . 【详解】 对于选项
10 BCD A,
. 【详解】 由 α β α β α β α β 得 α β α β .所
4 A sin cos -cos sin =3cos cos -3sin sin , tan -tan =3-3tan tan =-3 ( )
f π π 3
以 (α β) tan α -tan β -3 .故选 =-sin +sinπ=- ,
3 3 2
tan - = α β= =-1 :A.
1+tan tan 1+2 ( ) ( ) ( )
f 4π 4π 3 显然f π f 4 所以函数周期不为 故 错误
. 【详解】 由y mx2 m 得x2 1y. =-sin +sin4π= , ≠ π , π, A ;
5 D = ( >0), =m 3 3 2 3 3
对于选项
B,
因为第一象限点P n 在抛物线上且 FP 所以 1 即m 1. ( ) ( ) é ( )ù
( ,1) =2, 4 m+1=2, = 4 f π - x =-sin π - x +sinë ê ê 3 π - x û ú ú =-cos x -cos3 x ,
2 2 2
所以 1n2 得n 即m n 9. 故选 ( ) ( ) é ( )ù
1= 4 =2, + = 4 :D. f π + x =-sin π + x +sinë ê ê 3 π + x û ú ú =-cos x -cos3 x ,
. 【详解】 由S a a a 得S S S 即 S S 因为{nS }为等差数列 设其公 2 2 2
6 D 6+ 4+ 5+ 6=1, 6+ 6- 3=1, 6 6-3 3=3, n , ( ) ( )
n 所以f π x f π x 即函数图象关于直线x π对称 故 正确
差为d 则 S S d 即 d 所以 nS S (n ) d 即 nS n 所以 S +1 所以 - = + , = , B ;
, 6 6-3 3=3 , =1, n=1× 1+ -1 × , n= +1, n= n , 2 2 2
对于选项 选项
C,D ,
9
S f x x x
S 9 a S S 9 8 1 即 8 8 . 故选 ( )= -sin +sin3
8= , 8= 8- 7= - =- , a = =-63 :D. x x x x x
8 8 7 56 8 1 =-sin +sin cos2 +cos sin2
-
56 =-sin
x
+sin
x(
1-2sin
2x)
+2sin
x(
1-sin
2x)
. 【详解】 由对称性知 PO OQ 又O是线段F F 的中点 所以四边形F PF Q为平行四
7 B = , 1 2 , 1 2 =2sin x -4sin 3x
边形 所以 F Q F P 即 F P F Q F P 又 F P F P a 所以 F P ( )( )
, 1 = 2 , 1 =3 1 =3 2 , 1 - 2 =2 =6, 1 =9, 令f x 得 x 3x 即 x x 2 x 2
F P 又 F F c 由 PQ 2 F F 2 ( F P 2 F P 2 )代入数据 得 PQ . ( )= 0, 2sin -4sin =0, -4sin sin - sin + =0,
2 =3, 1 2 =2 =10, + 1 2 =2 1 + 2 , =4 5 2 2
故选
:B.
所以 x 或 x 2 或 x 2
. 【详解】 由f x f(x) x 得f x f(x ) x 即f x f(x) x sin =0, sin = , sin =- ,
8 B ( +1)- ≥ , ( +2)- +1 ≥ +1, ( +2)- ≥2 +1, 2 2
又因为f x f(x) x 所以f x f(x) x
( +2)- ≤2 +1, ( +2)- =2 +1, 由x [ ] 解得x x π x 3 x x 5 x 7 x
即f f( ) f f( ) f f( ) ∈ 0,2π , 1=0, 2= , 3= π, 4=π, 5= π, 6= π, 7=2π,
(3)- 1 =3, (5)- 3 =7, (7)- 5 =11, 4 4 4 4
所以函数有 个零点 故 正确
︙ 7 , C ;
( ) f′ x x( 2x)
f f( ) 所以f f( ) 3+79 ×20 ( )= 2cos 1-6sin ,
(41)- 39 =79, (41)- 1 =3+7+11+…+79= =820,
2 当π x π时 x 1 2x 2x 所以f′ x
即f f( ) .故选 < < ,cos >0, > >0, - >0 + >0。 a c- a >0, ( ) , , D . :BCD.
+ + + 4 2V
11
.
ABD
【详解】 设圆柱底面半径为r
,
母线长为l
,
则
:
V
=π
r2l
,
得l
= r2
(r
>0
)
,
因为n
=
1- 5
≈-0
.
6,
所以
0<
n12
<1,
即
[
m12
]=321
.
π 2
V
所以S r2 rl r2 2 . π
=2π +2π =2π + r , 15 (1) (2)6+2 3
3
( V ) 【详解】 由A B C 得 A B C 分
r3 (1) + + =π, sin =sin( + ),(1 )
令f
(
r
)= 2π
r2
+
2
r
V (r
>0
)
,
f′
(
r
)= 4π
r
-
2
r
V
2 =
4π r
r
3
2
-2 V
=
4π
r2
- 2π
,
即
sin(
B
-
C
)=sin
B
-sin(
B
+
C
),
所以 B C B C B B C B C
sin cos -cos sin =sin -sin cos -cos sin ,
3 V 3 V
当 r 时 f′(r) f (r)单调递减 当r 时 f′(r) f(r)单调递增 即 B C B 分
0< < , <0, ; > , >0, , 2sin cos =sin ,(4 )
2π 2π
( ) 因为 B 所以 C 1
3 V 3 V 2 V V V sin ≠0, cos = ,
所以当r 时 f (r) 2 3 .即S 3 . 2
= , min=2π + 3 V = 3 V ≥ 3 V
2π 2π
因为 C 所以C π. 分
0< <π, = (6 )
2π 2π 2π 3
S3
故 .代入数据 故选 由S 1ab C 得 1ab π 即ab 分
V2 ≥54π , :ABD. (2) Δ ABC= sin , 2 3= sin , =8,(8 )
2 2 3
12
.
2 2
【详解】 因为
{
a
n}
是等比数列
,
设其公比为 q
,
则 a
6=
a
2
q4
,
q4
=8,
所以 q2
=2 2
. 所以
由c2 a2 b2 ab C 得 2 a2 b2 ab π 即a2 b2 分
= + -2 cos , (2 3) = + -2 cos , + =20,(10 )
a a q2 . 3
{
4= 2 =2 2
}
所以a2
+
b2
+2
ab
=36,
解得a
+
b
=6
.
(12
分
)
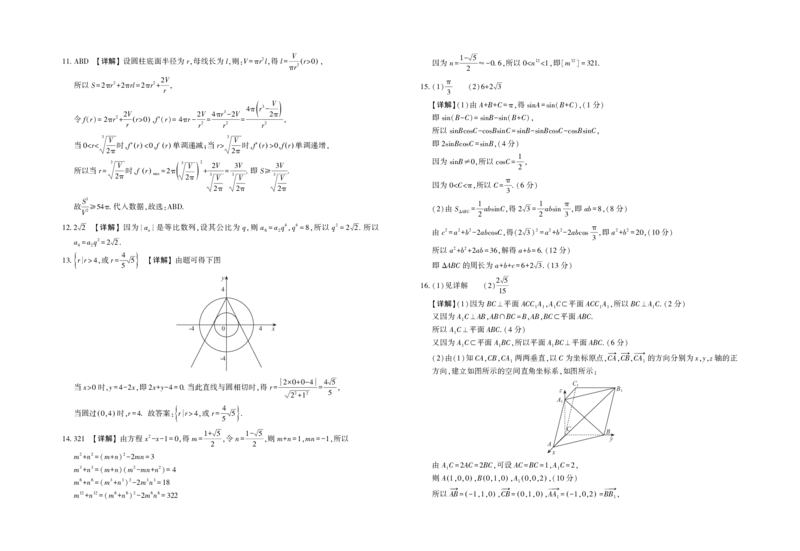
. r r 或r 4 【详解】 由题可得下图
13 >4, = 5 即 ABC的周长为a b c . 分
5 Δ + + =6+2 3 (13 )
y
. 见详解 2 5
4 16 (1) (2)
15
【详解】 因为BC 平面ACC A A C 平面ACC A 所以BC A C. 分
(1) ⊥ 1 1, 1 ⊂ 1 1, ⊥ 1 (2 )
又因为A C AB AB BC B AB BC 平面ABC.
1 ⊥ , ∩ = , , ⊂
-4 0 4 x 所以A C 平面ABC. 分
1 ⊥ (4 )
又因为A C 平面A BC 所以平面A BC 平面ABC. 分
1 ⊂ 1 , 1 ⊥ (6 )
-4 由 知CA CB CA 两两垂直 以C为坐标原点 C→A C→B C→A 的方向分别为x y z轴的正
(2) (1) , , 1 , , , , 1 , ,
方向 建立如图所示的空间直角坐标系 如图所示
, , :
C
当x >0 时 , y =4-2 x , 即 2 x + y -4=0 .当此直线与圆相切时 , 得r = 2×0+0-4 = 4 5 , z 1 B 1
2 2 +1 2 5 A 1
{ }
当圆过( )时 r . 故答案 r r 或r 4 .
0,4 , =4 : >4, = 5
5
C
B
. 【详解】 由方程x2 x 得m 1+ 5 令n 1- 5 则m n mn 所以 y
14 321 - -1=0, = , = , + =1, =-1, A
2 2
x
m2 n2 m n 2 mn
+ =( + ) -2 =3
由A C AC BC 可设AC BC A C
m3 + n3 =( m + n )( m2 - mn + n2 )= 4 则A 1 ( =2 ) = B 2 ( , ) A ( = = ) 1, 1 = 分 2,
m6 + n6 =( m3 + n3 ) 2 -2 m3n3 =18 1,0,0 , 0,1,0 , 1 0,0,2 ,(10 )
m12 + n12 =( m6 + n6 ) 2 -2 m6n6 =322 所以A→B = ( -1,1,0 ) , C→B = ( 0,1,0 ) , A→A 1= ( -1,0,2 ) = BB→ 1,所以AB→ A→B BB→ ( ) ( ) ( ) 【详解】 (1) 当a =2 时 , f (x) = x2 -3 x +ln x , 所以f ( 1 ) =1 2 -3×1+ln1=-2,(1 分 )
1= + 1= -1,1,0 + -1,0,2 = -2,1,2 ,
设→n (x y z)为平面BCC B 的法向量 且f′(x) x 1 所以f′( ) 1 分
= , , 1 1 , =2 -3+x , 1 =2×1-3+ =0,(2 )
1
则 { →n · C→B = y =0, 取→n ( ) 分 所以切线方程为y - ( -2 ) =0× (x -1 ) , 即y =-2 . (4 分 )
→n BB→ x z = 2,0,1 ,(12 ) ax2 ( a)x (x )(ax )
· 1=- +2 =0, 由题意可得x f′(x) ax ( a) 1 - 1+ +1 -1 -1 分
设直线AB 与平面BCC B 所成的角为θ (2) >0, = - 1+ +x = x = x (5 )
1 1 1 ,
x
AB→ →n 当a 时 f′(x) 1-
则 θ AB→ →n 1· 2 2 5 =0 , = x ,
sin = cos〈 1, 〉 =
AB→
1 ·
→n
=
3 5
=
15
,
令f′(x) 可得 x 所以f(x)在区间( )上单调递增
>0 0< <1, 0,1 ;
令f′(x) 可得x 所以f(x)在区间( �)上单调递减 分
即直线AB 与平面BCC B 所成角的正弦值为2 5. 分 <0 >1, 1,+ ;(6 )
1 1 1 (15 ) ( )
15
17
.
(1)
见详解
(2)
(-1-3 n )(-2) n +1 -2
-
n ( n +1) 当a 时 f′(x) a(x -1 ) x - a 1
<0 , = x ,
9 2
【详解】 因为 a n +1+1 -2 a n-3+1 分 令f′(x) >0, 可得 0< x <1, 所以f(x)在区间( 0,1 )上单调递增 ;
(1) a = a =-2,(3 )
n+1 n+1 令f′(x) 可得x 所以f(x)在区间( �)上单调减 分
<0 >1, 1,+ ;(7 )
且a 所以数列{a }是等比数列. 分
n+1≠0, n+1 (4 ) ( )
a(x ) x 1
(2) 由 (1) 得数列{a n+1 }是等比数列 , 且公比q =-2, 当 a 时 f′(x) -1 - a
所以a
n+1=(
a
1+1)
qn -1
=(-2)×(-2)
n -1
=(-2)
n
,
0< <1 , = x ,
故a n . 分
n=(-2) -1 (6 ) 令f′(x) 可得 x 或x 1
>0 0< <1, >a,
所以na n n n. 分
n= (-2) - (7 ) ( )
故S n =1×(-2)-1+2×(-2) 2 -2+3×(-2) 3 -3+… n (-2) n - n 所以f (x)在区间( 0,1 )上单调递增 , f (x)在区间 1 a,+ � 上单调递增 ;
=1×(-2)+2×(-2) 2 +3×(-2) 3 +…+ n (-2) n -(1+2+3+…+ n ) ( )
令f′(x) 可得 x 1 所以f (x)在区间 1 上单调递减 分
n n
2 3 n n (1+ ) 分 <0 1< 1 , = x ,
(-2)×[1-(-2) ] n n +1
= - (-2)
1-(-2) 令f′(x) 可得 x 1 或x
n n +1 >0 0< 1,
(-1-3 )(-2) -2 分
= (13 ) ( )
3 所以f (x)在区间 1 上单调递增 f (x)在区间( �)上单调递增
n n +1 0,a , 1,+ ;
所以T (-1-3 )(-2) -2 分
n= (14 ) ( )
9 令f′(x) 可得1 x 所以f (x)在区间 1 上单调递减 分
n n +1 n n <0 a < <1, a,1 ;(10 )
即S (-1-3 )(-2) -2 ( +1) 分
n= - (15 ) 综上
9 2 :
. y 见详解 当a 时 f (x)在区间( )上单调递增 f (x)在区间( �)上单调递减
18 (1) =-2 (2) (3)ln2-2 ≤0 , 0,1 ; 1,+ ;( ) ì t
当 a 时 f (x)在区间( )上单调递增 f (x)在区间 1 � 上单调递增 ï y (x )
0< <1 , 0,1 , a,+ ; ïï = +2
f (x)在区间
(
1
)
上单调递减
联立直线AM和椭圆方程í
ïx2
6
y2 ,
消去y可得(
27+
t2 )x2
+4
t2x
+4
t2
-108=0,
ï
1,a ; î + =1
4 3
当a
=1
时
,
f (x)在区间(
0,+
�)上单调递增
; 由韦达定理可得 x 4
t2
-108 解得x 54-2
t2
则y
t
(x ) 18
t
分
当a 时 f (x)在区间
(
1
)
上单调递增 f (x)在区间( �)上单调递增
-2 P=
27+
t2 , P=
27+
t2 , P=
6
P+2 =
27+
t2 ;(8 )
>1 , 0,a , 1,+ ;
ì t
ï y (x )
( ) ïï = -2
f (x)在区间 1
a,1
上单调递减.
(11
分
)
联立直线BM和椭圆方程í
ïx2
2
y2 ,
消去y可得(
3+
t2 )x2
-4
t2x
+4
t2
-12=0,
由 得当a 时 f(x)在区间( )上单调递增 f(x)在区间( �)上单调递减. î ï + =1
(3) (2) <0 , 0,1 ; 1,+ 4 3
所以f x f
a
分 由韦达定理可得 x 4
t2
-12 解得x 2
t2
-6 则y
t
(x ) 6
t
分
( )max= (1)= -1-
2
,(12 ) 2 q=
3+
t2 , q=
3+
t2 , q=
2
q-2 =-
3+
t2 ;(10 )
由题意得只需b a a a 即b a a . 分 ( t2 t ) ( t2 t )
-ln(- )- ≥-1- , ≥ln(- )-1+ (13 ) 则B→P 54-2 18 -4 18
2 2 = t2 -2, t2 = t2 , t2 ,
27+ 27+ 27+ 27+
a a
令g a a a 则g′ a 1 1 +2 分 ( t2 t ) ( t )
( )=ln(- )-1+ ( <0), ( )= a + = a ,(14 ) B→Q 2 -6 6 -12 6
2 2 2 = t2 -2,- t2 = t2 ,- t2 ,
当a 时 g′ a g a 单调递增
3+ 3+ 3+ 3+
<-2 , ( )>0, ( ) ; t2 ( ) t ( t ) t2
当 a 时 g′ a g a 单调递减 所以B→P B→Q -4 12 18 6 -60
-2< <0 , ( )<0, ( ) ; · = t2 × - t2 + t2 × - t2 =( t2 )( t2 )<0,
27+ 3+ 27+ 3+ 27+ 3+
即g a g 分
( )max= (-2)=ln2-2,(16 ) 即 PBQ为钝角. 分
∠ (12 )
所以只需b 即b最小值为 . 分
≥ln2-2, ln2-2 (17 ) 由 四边形APBQ面积为
(ⅱ) (ⅰ)
.
x2 y2
见详解 ( t t ) t( t2 )
19 (1) + =1 (2)(ⅰ) (ⅱ)6 S 1 AB y y 18 6 48 9+ 48 分
4 3 = × × p- q =2 t2 + t2 =( t2 ) 2 t2 = t2 t,(14 )
【详解】 设T(x
0,
y
0
)
,
则
a
x2 0
2 +
y
b
2 0
2 =1,
即y2
0=
(
1-a
x2 0
2
) b2. 2 27+ 3+ 9+ +12 9+ t +
9
1
+
2 t2
t2 t2
由A( a ) B a 得 设λ 9+ t 则λ 9+ 9 t 9 t 当且仅当t 时等号成立
- ,0 , ( ,0), = t , >0, = t = t + ≥2 t × =6, =3 ,
( x2 )
k k y 0-0 y 0-0 y2 0 1-a
0
2
b2
b2 3 分 由对勾函数性质可知y = λ + 1 λ 2在[ 6,+ �)上单调递增 ,
TA TB=x a×x a=x2 a2 = x2 a2 =-a2 =- (2 )
0+ 0- 0- 0- 4
所以y λ 12 可得 S 48 48 所以 t 时 四边形 APBQ 的面积最大为
当点T在椭圆的上顶点时 S 1 AB OT 1 a b ab 分 = +λ≥6+2=8, = ≤ =6, =3 , 6,
, ΔATB= × = ×2 × = =2 3,(4 ) λ 12 8
+λ
2 2
解得a b .故椭圆C的方程为
x2 y2
. 分 此时点M的坐标为( ) 分
=2, = 3 + =1 (5 ) 4,3 ,(16 )
4 3 由对称性可知 即当点M的坐标为( )或( )时 四边形APBQ的面积最大 最大值为 .
易知 A( ) B( ) 由椭圆对称性可知 不妨设 M( t) t P (x y ) , 4,3 4,-3 , , 6
(2)(ⅰ) -2,0 , 2,0 , , 4, , >0, p, p , 分
Q(x y ) (17 )
q, q ,
t t
根据题意可知直线AM BM斜率均存在 且k k
, , MA= , BM= ,
6 2
t t
所以直线AM的方程为y (x ) BM的方程为y (x )
= +2 , = -2 ,
6 2